11.2 反比例函数的图像与性质(第2课时)(共30张PPT)
文档属性
| 名称 | 11.2 反比例函数的图像与性质(第2课时)(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 18:00:35 | ||
图片预览









文档简介
11.2 反比例函数的图像与性质
第2课时
第11章 反比例函数
2020-2021学年度苏科版八年级下册
1. 反比例函数的定义:
叫做反比例函数.
函数
2. 反比例函数的特征:
k ≠0, x ≠0.x是-1次
复习回顾
函数图象画法
列
表
描
点
连
线
描点法
反比例函数的图象又会是什么样子呢?
你还记得作函数图象的一般步骤吗?
用图象法表示函数关系时,首先在自变量的取值范围内取一些值,列表,描点,连线(按自变量从小到大的顺序,用一条平滑的曲线连接起来).
x
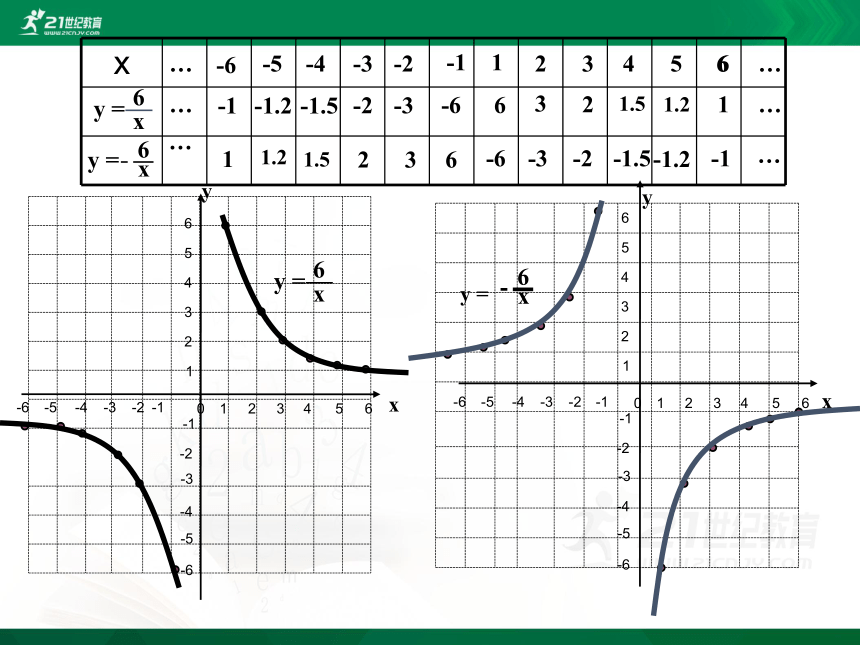
画出反比例函数 和
的函数图象.
y =
x
6
y =
x
6
y =
x
6
y =
x
6
合作学习
列
表
描
点
连
线
描点法
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
x
y =
x
6
y =
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
y =
x
6
y =
x
6
2. 反比例函数 的图象在哪两个象限?由什么确定?
3. 反比例函数 ,具有怎样的对称性?
4. 反比例函数 的图象的变化趋势是怎样的,它和两条坐标轴的位置关系是怎样的?
1. 反比例函数 和 的图象在哪两个象限?它们相同吗?
y =
x
6
x
y
0
y
x
x
6
y =
0
合作学习
1.当k>0时,图象的两个分支分别在第一、三象限内;
2.当k<0时,图象的两个分支分别在第二、四象限内.
y
x
y
x
6
y =
0
3.图象的两个分支关于直角坐标系的原点成中心对称.
x
0
如果知道双曲线的一支,利用对称性,如何画另一支?
4.双曲线无限接近于x、y轴,但永远不会与坐标轴相交.
合作学习
y =
x
6
x
y
0
一般地,反比例函数 (k≠0)的图象有下面的性质:
图象是双曲线
当k>0时,双曲线分别位于第一,三象限内;
当k<0时, 双曲线分别位于第二,四象限内.
双曲线是中心对称图形.
形 状
位 置
变化趋势
对称性
双曲线无限接近于x、y轴,但永远不会与坐标轴相交.
解:(1)因为函数 的图像经过点A(2,-4),把x=2、y=-4代入 ,得-4= 解得k=-8;
(2)因为k=-8<0,由反比例函数的性质可知,函数
的图像在第二、四象限,在每一个象限内,y随x的增大而增大;
例1 已知反比例函数 的图像经过点A(2,-4),
(1)求k的值;
(2)函数的图像在哪几个象限?y随x的增大怎样变化?
(3)画出函数的图像;
(4)点B( ,-16)、C(-3,5)在这个函数的图像上吗?
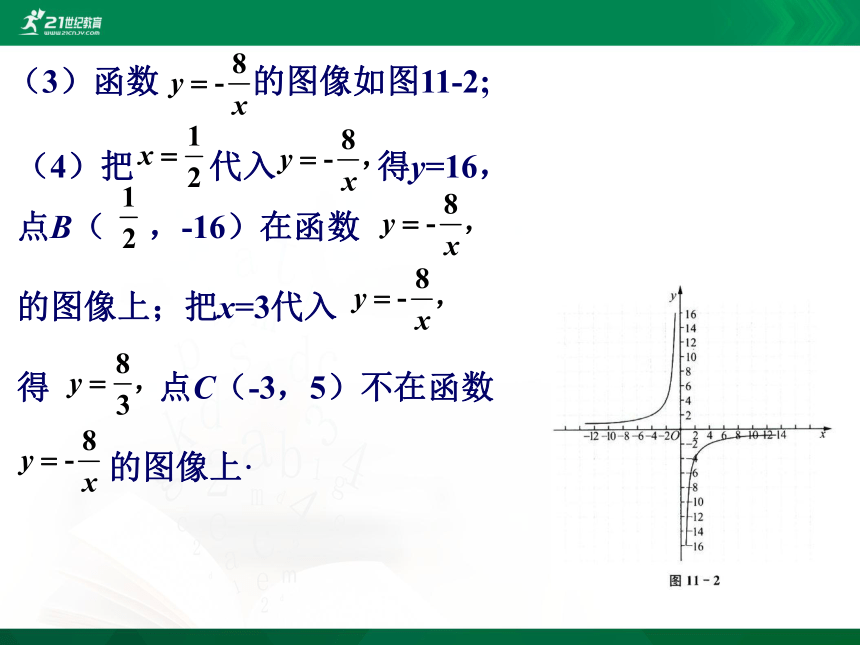
(3)函数 的图像如图11-2;
(4)把 代入 得y=16,点B( ,-16)在函数
的图像上;把x=3代入
得 点C(-3,5)不在函数
的图像上·
解:(1)由“菱形的面积等于它的两条对角线长的乘积的一半”,得
y与x的函数表达式为 y是x的反比例函数.
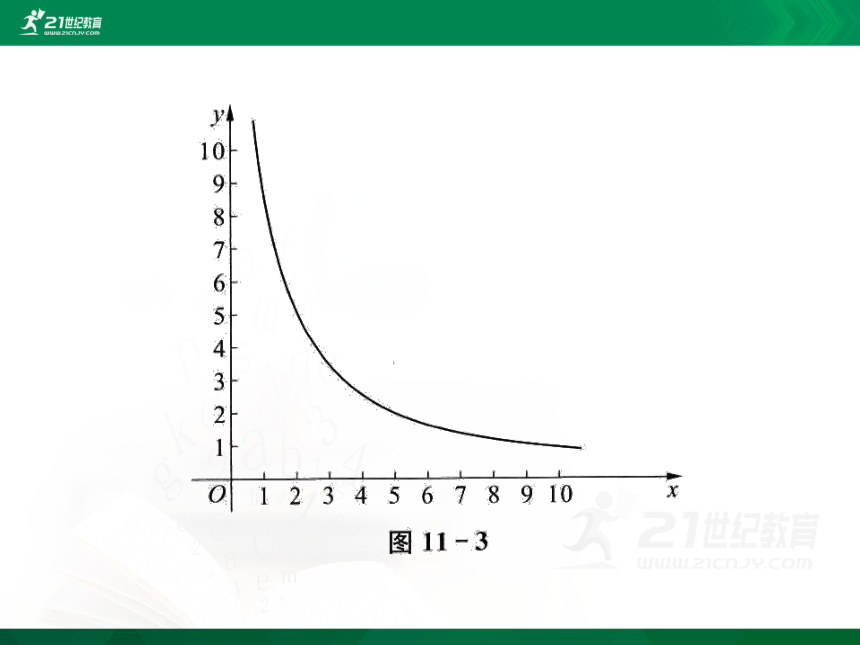
(2)根据题意,可知x>0.
反比例函数 ( x >0)的图像是其在第一象限的一支,如图11-3.
例2 设菱形的面积是5cm2,两条对角线的长分别是xcm、ycm.
(1)确定y与x的函数表达式;
(2)画出这个函数的图像.
解:(1)把x=-3代入y=x+1,得y=-2.
根据题意,可得反比例函数
的图像与一次函数y=x+1的图像的一个交点的坐标是
(-3,-2).
例3 已知反比例函数 的图像与一次函数y=x+1的图像的一个交点的横坐标是-3.
(1)求k的值,并画出这个反比例函数的图像;
(2)根据反比例函数的图像,指出当k<-1时,y的取值范围.
把x=-3、y=-2代入 得
即k=6.
函数 的图像如图11-4.
(2)由函数图像知,当x<-1时,-61.函数 的图象在第__________象限,
2. 双曲线 经过点(-3,___)
y =
x
5
y =
1
3x
二,四
9
1
3.函数 的图象在二、四象限,则m的取值范围是 ____ .
4.对于函数 ,当 x<0时,图象在第 ________象限.
m-2
x
y =
m < 2
三
y =
1
3x
练习
当 时,在 内,
随 的增大而 .
O
反比例函数 的图象:
A
B
O
C
D
A
B
C
D
减少
每个象限
当 时,在 内,
随 的增大而 .
增大
每个象限
反 比 例
函 数
图 象
图象的
位置
图 象 的
对 称 性
增 减 性
(k > 0)
(k < 0)
y =
x
k
y =
x
k
x
y
0
y
x
0
当k>0时,在每一象限内,函数值y随自变量x的增大而减小.
当k<0时,在每一象限内函数值y随自变量x的增大而增大.
两个分支关于原点成中心对称
两个分支关于原点成中心对称
在第一、
三象限内
在第二、
四象限内
学生总结:反比例函数的性质
提高练习
1、图1是正比例函数y=-kx的图像,则反比例函数 的图像最有可能是 ( ).
x
y
x
y
x
y
x
y
x
y
图1
A
B
C
D
O
O
O
O
O
D
提高练习
2、如图,动点P在反比例函数 图像的一个分支上,过点P作PA⊥x轴于点A、PB⊥y轴于点B,当点P移动时,△OAB的面积大小是否变化?为什么?
x
y
O
A
B
P
已知点A(1,4)是双曲线 的一点,过点A作x轴的垂线段PA垂足为P,过点A作AB⊥y轴于B点.得到长方形OPAB.
(1)你能说出长方形OPAB的面积吗?
(2)若A点是该双曲线上的一个动点,分别过点A给坐标轴作垂线段得到的长方形面积是否发生变化?若不变,请求出其面积;若改变,试说明理由.
A
O
P
x
y
B
1、如图,点P是反比例函数 图象上的一点,PD⊥x轴于D.
则△POD的面积为_______.
D
o
y
P
x
2、如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为12,则这个反比例函数的关系式是__________ .
x
y
o
M
N
p
P(m,n)
A
o
y
x
B
P(m,n)
A
o
y
x
B
说说你的推理
过点P分别作x轴,y轴的垂线段,垂足为A,B,
则S矩形OAPB=OA·AP=|m|·|n|=|k|.
上任意一点,
是双曲线
)
,
(
n
m
P
P(m,n)
A
o
y
x
P(m,n)
A
o
y
x
则
垂足为
轴的垂线
作
过
,
,
)
1
(
A
x
P
有
上任意一点
是双曲线
设
:
,
)
,
(
n
m
P
P(m,n)
A
o
y
x
P(m,n)
A
o
y
x
想一想
若将此题改为过P点作y轴的垂线段,其结论成立吗?
你认为作反比例函数图像时应注意哪些问题?与同伴进行交流.
(1)列表时,选取的自变量的值既要易于计算又要便于描点,尽量多取一些数值(取互为相反数的一对一对的数),多描一些点,这样既可以方便连线,又可以使图象精确.
(2)描点时要严格按照表中所列的对应值描点,绝对不能把点的位置描错.
(3)一定要按自变量从小到大的顺序依次画线,连线时必须用光滑的曲线连接各点,不能用折线连接.
(4)图像是延伸的,注意不要画成有明确端点.
(5)曲线的发展趋势只能靠近坐标轴,但不能和坐标轴相交.
反比例函数的图象与性质:
课堂小结
反 比 例
函 数
图 象
图象的
位置
图 象 的
对 称 性
增 减 性
(k > 0)
(k < 0)
y =
x
k
y =
x
k
x
y
0
y
x
0
当k>0时,在每一象限内,函数值y随自变量x的增大而减小.
当k<0时,在每一象限内函数值y随自变量x的增大而增大.
两个分支关于原点成中心对称
两个分支关于原点成中心对称
在第一、
三象限内
在第二、
四象限内
谢谢聆听
第2课时
第11章 反比例函数
2020-2021学年度苏科版八年级下册
1. 反比例函数的定义:
叫做反比例函数.
函数
2. 反比例函数的特征:
k ≠0, x ≠0.x是-1次
复习回顾
函数图象画法
列
表
描
点
连
线
描点法
反比例函数的图象又会是什么样子呢?
你还记得作函数图象的一般步骤吗?
用图象法表示函数关系时,首先在自变量的取值范围内取一些值,列表,描点,连线(按自变量从小到大的顺序,用一条平滑的曲线连接起来).
x
画出反比例函数 和
的函数图象.
y =
x
6
y =
x
6
y =
x
6
y =
x
6
合作学习
列
表
描
点
连
线
描点法
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
x
y =
x
6
y =
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
y =
x
6
y =
x
6
2. 反比例函数 的图象在哪两个象限?由什么确定?
3. 反比例函数 ,具有怎样的对称性?
4. 反比例函数 的图象的变化趋势是怎样的,它和两条坐标轴的位置关系是怎样的?
1. 反比例函数 和 的图象在哪两个象限?它们相同吗?
y =
x
6
x
y
0
y
x
x
6
y =
0
合作学习
1.当k>0时,图象的两个分支分别在第一、三象限内;
2.当k<0时,图象的两个分支分别在第二、四象限内.
y
x
y
x
6
y =
0
3.图象的两个分支关于直角坐标系的原点成中心对称.
x
0
如果知道双曲线的一支,利用对称性,如何画另一支?
4.双曲线无限接近于x、y轴,但永远不会与坐标轴相交.
合作学习
y =
x
6
x
y
0
一般地,反比例函数 (k≠0)的图象有下面的性质:
图象是双曲线
当k>0时,双曲线分别位于第一,三象限内;
当k<0时, 双曲线分别位于第二,四象限内.
双曲线是中心对称图形.
形 状
位 置
变化趋势
对称性
双曲线无限接近于x、y轴,但永远不会与坐标轴相交.
解:(1)因为函数 的图像经过点A(2,-4),把x=2、y=-4代入 ,得-4= 解得k=-8;
(2)因为k=-8<0,由反比例函数的性质可知,函数
的图像在第二、四象限,在每一个象限内,y随x的增大而增大;
例1 已知反比例函数 的图像经过点A(2,-4),
(1)求k的值;
(2)函数的图像在哪几个象限?y随x的增大怎样变化?
(3)画出函数的图像;
(4)点B( ,-16)、C(-3,5)在这个函数的图像上吗?
(3)函数 的图像如图11-2;
(4)把 代入 得y=16,点B( ,-16)在函数
的图像上;把x=3代入
得 点C(-3,5)不在函数
的图像上·
解:(1)由“菱形的面积等于它的两条对角线长的乘积的一半”,得
y与x的函数表达式为 y是x的反比例函数.
(2)根据题意,可知x>0.
反比例函数 ( x >0)的图像是其在第一象限的一支,如图11-3.
例2 设菱形的面积是5cm2,两条对角线的长分别是xcm、ycm.
(1)确定y与x的函数表达式;
(2)画出这个函数的图像.
解:(1)把x=-3代入y=x+1,得y=-2.
根据题意,可得反比例函数
的图像与一次函数y=x+1的图像的一个交点的坐标是
(-3,-2).
例3 已知反比例函数 的图像与一次函数y=x+1的图像的一个交点的横坐标是-3.
(1)求k的值,并画出这个反比例函数的图像;
(2)根据反比例函数的图像,指出当k<-1时,y的取值范围.
把x=-3、y=-2代入 得
即k=6.
函数 的图像如图11-4.
(2)由函数图像知,当x<-1时,-6
2. 双曲线 经过点(-3,___)
y =
x
5
y =
1
3x
二,四
9
1
3.函数 的图象在二、四象限,则m的取值范围是 ____ .
4.对于函数 ,当 x<0时,图象在第 ________象限.
m-2
x
y =
m < 2
三
y =
1
3x
练习
当 时,在 内,
随 的增大而 .
O
反比例函数 的图象:
A
B
O
C
D
A
B
C
D
减少
每个象限
当 时,在 内,
随 的增大而 .
增大
每个象限
反 比 例
函 数
图 象
图象的
位置
图 象 的
对 称 性
增 减 性
(k > 0)
(k < 0)
y =
x
k
y =
x
k
x
y
0
y
x
0
当k>0时,在每一象限内,函数值y随自变量x的增大而减小.
当k<0时,在每一象限内函数值y随自变量x的增大而增大.
两个分支关于原点成中心对称
两个分支关于原点成中心对称
在第一、
三象限内
在第二、
四象限内
学生总结:反比例函数的性质
提高练习
1、图1是正比例函数y=-kx的图像,则反比例函数 的图像最有可能是 ( ).
x
y
x
y
x
y
x
y
x
y
图1
A
B
C
D
O
O
O
O
O
D
提高练习
2、如图,动点P在反比例函数 图像的一个分支上,过点P作PA⊥x轴于点A、PB⊥y轴于点B,当点P移动时,△OAB的面积大小是否变化?为什么?
x
y
O
A
B
P
已知点A(1,4)是双曲线 的一点,过点A作x轴的垂线段PA垂足为P,过点A作AB⊥y轴于B点.得到长方形OPAB.
(1)你能说出长方形OPAB的面积吗?
(2)若A点是该双曲线上的一个动点,分别过点A给坐标轴作垂线段得到的长方形面积是否发生变化?若不变,请求出其面积;若改变,试说明理由.
A
O
P
x
y
B
1、如图,点P是反比例函数 图象上的一点,PD⊥x轴于D.
则△POD的面积为_______.
D
o
y
P
x
2、如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为12,则这个反比例函数的关系式是__________ .
x
y
o
M
N
p
P(m,n)
A
o
y
x
B
P(m,n)
A
o
y
x
B
说说你的推理
过点P分别作x轴,y轴的垂线段,垂足为A,B,
则S矩形OAPB=OA·AP=|m|·|n|=|k|.
上任意一点,
是双曲线
)
,
(
n
m
P
P(m,n)
A
o
y
x
P(m,n)
A
o
y
x
则
垂足为
轴的垂线
作
过
,
,
)
1
(
A
x
P
有
上任意一点
是双曲线
设
:
,
)
,
(
n
m
P
P(m,n)
A
o
y
x
P(m,n)
A
o
y
x
想一想
若将此题改为过P点作y轴的垂线段,其结论成立吗?
你认为作反比例函数图像时应注意哪些问题?与同伴进行交流.
(1)列表时,选取的自变量的值既要易于计算又要便于描点,尽量多取一些数值(取互为相反数的一对一对的数),多描一些点,这样既可以方便连线,又可以使图象精确.
(2)描点时要严格按照表中所列的对应值描点,绝对不能把点的位置描错.
(3)一定要按自变量从小到大的顺序依次画线,连线时必须用光滑的曲线连接各点,不能用折线连接.
(4)图像是延伸的,注意不要画成有明确端点.
(5)曲线的发展趋势只能靠近坐标轴,但不能和坐标轴相交.
反比例函数的图象与性质:
课堂小结
反 比 例
函 数
图 象
图象的
位置
图 象 的
对 称 性
增 减 性
(k > 0)
(k < 0)
y =
x
k
y =
x
k
x
y
0
y
x
0
当k>0时,在每一象限内,函数值y随自变量x的增大而减小.
当k<0时,在每一象限内函数值y随自变量x的增大而增大.
两个分支关于原点成中心对称
两个分支关于原点成中心对称
在第一、
三象限内
在第二、
四象限内
谢谢聆听
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
