2020——2021学年人教版八年级数学下册课件-18.1.1 平行四边形的性质(共13张)
文档属性
| 名称 | 2020——2021学年人教版八年级数学下册课件-18.1.1 平行四边形的性质(共13张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 00:00:00 | ||
图片预览


文档简介
第十八章 平行四边形
18.1.1 平行四边形的性质
第1课时
义务教育教科书( RJ )八年级数学下册
人教版 八年级数学下册
新课导入
观察这些图片,它们是否都有平行四边形的形象?
拼 一 拼
取两个全等的三角形纸片,将它们相等的一边重合,得到一个四边形。
你拼出了怎样的四边形?
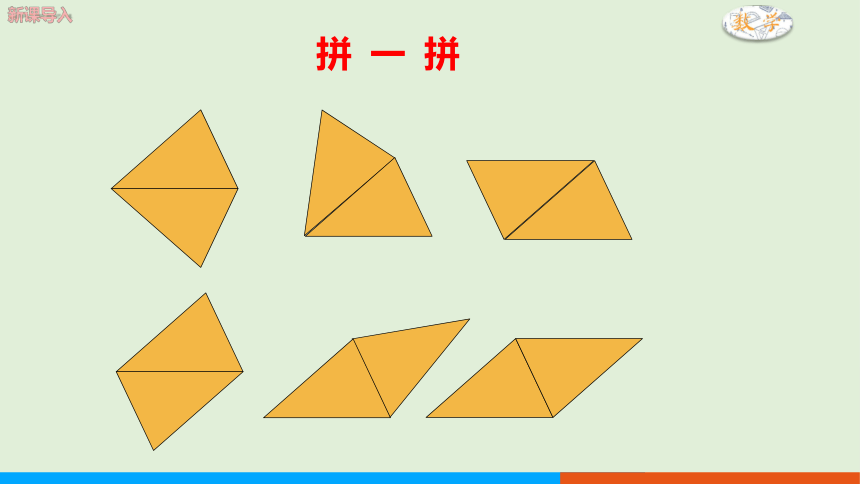
拼 一 拼
知识讲解
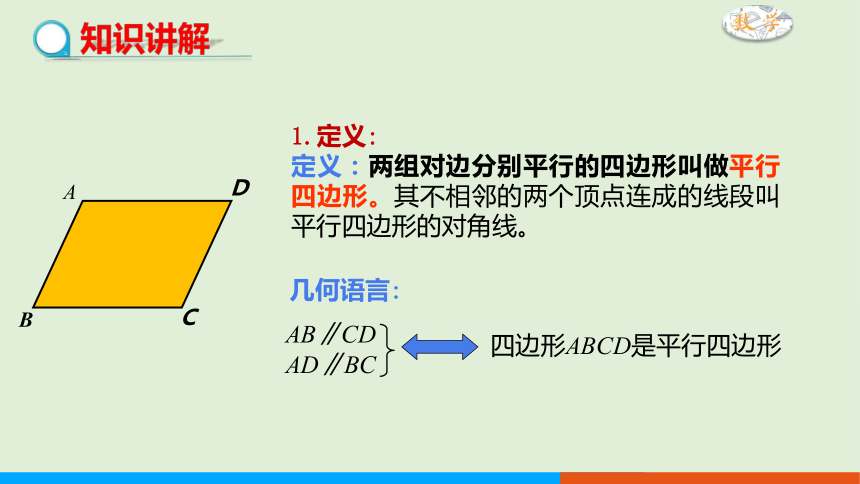
1.定义:
定义:两组对边分别平行的四边形叫做平行四边形。其不相邻的两个顶点连成的线段叫平行四边形的对角线。
A
B
D
C
几何语言:
四边形ABCD是平行四边形
AB∥CD
AD∥BC
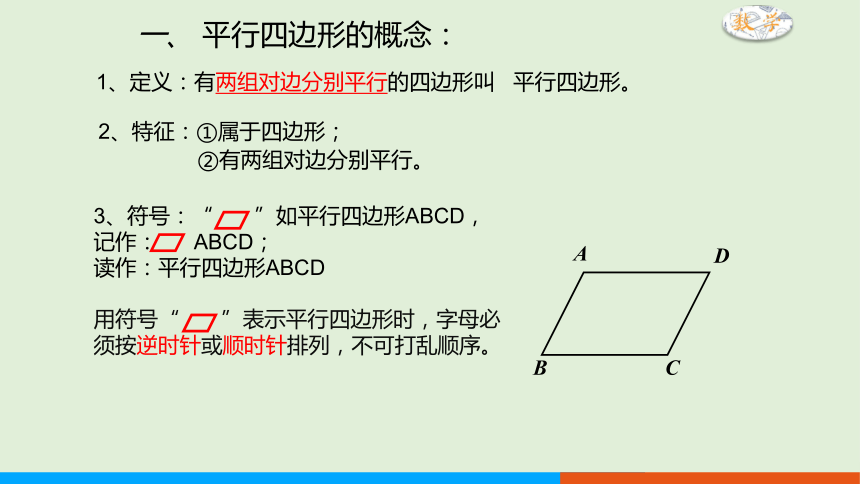
一、 平行四边形的概念:
1、定义:有两组对边分别平行的四边形叫 平行四边形。
2、特征:①属于四边形;
②有两组对边分别平行。
3、符号:“ ”如平行四边形ABCD, 记作: ABCD;
读作:平行四边形ABCD
用符号“ ”表示平行四边形时,字母必须按逆时针或顺时针排列,不可打乱顺序。
A
D
C
B
思考:根据定义画一个平行四边形,观察这个四边形,除了 “两组对边分别平行”以外,它的边、角之间有什么关系吗?度量一下,是不是和你的猜想一致?还有别的方法吗?
A
B
C
D
答:平行四边形的对边相等
平行四边形的对角相等
平行四边形的邻角互补
平行四边形的对边相等
平行四边形的对角相等
平行四边形的邻角互补
我们可以通过下面的动画来验证一下:
演 示
已知: ABCD
求证:AB=DC,BC=AD;
∠B=∠D,∠A=∠C.
A
B
C
D
证一证
1
2
3
4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
在△ABC和△CDA中
证明:连接AC
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∴AB=DC,BC=AD,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
即∠BAD=∠DCB
利用三角形全等得出全等三角形的对应边、对应角都相等,是证明线段相等、角相等的一种重要的方法。为此,我们通过添加辅助线,构造两个三角形,通过三角形全等进行证明。
平行四边形的性质
几何语言:
性质1:平行四边形的对边相等
性质2:平行四边形的对角相等
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC.(平行四边形的对边相等)
∵ 四边形ABCD是平行四边形
∴ ∠B=∠D,∠A=∠C.(平行四边形的对角相等).
随堂训练
判断题:(对的在括号内填“√”,错的填“×”)
(1)平行四边形两组对边分别平行且相等. ( )
(2)平行四边形的四个内角都相等. ( )
(3)平行四边形的相邻两个内角的和等于180°。( )
(4)如果平行四边形相邻两边长分别是2cm和3cm,那么周长10cm. ( )
(5)在平行四边形ABCD中,如果∠A=42°,那么∠B=48°. ( )
(6)在平行四边形ABCD中,如果∠A=35°, 那么∠C=145°. ( )
√
√
√
×
×
×
课堂小结
定义
两组对边分别平行的四边形
性质
平行四边形的对边相等
平行四边形的对角相等
平行
四边形
18.1.1 平行四边形的性质
第1课时
义务教育教科书( RJ )八年级数学下册
人教版 八年级数学下册
新课导入
观察这些图片,它们是否都有平行四边形的形象?
拼 一 拼
取两个全等的三角形纸片,将它们相等的一边重合,得到一个四边形。
你拼出了怎样的四边形?
拼 一 拼
知识讲解
1.定义:
定义:两组对边分别平行的四边形叫做平行四边形。其不相邻的两个顶点连成的线段叫平行四边形的对角线。
A
B
D
C
几何语言:
四边形ABCD是平行四边形
AB∥CD
AD∥BC
一、 平行四边形的概念:
1、定义:有两组对边分别平行的四边形叫 平行四边形。
2、特征:①属于四边形;
②有两组对边分别平行。
3、符号:“ ”如平行四边形ABCD, 记作: ABCD;
读作:平行四边形ABCD
用符号“ ”表示平行四边形时,字母必须按逆时针或顺时针排列,不可打乱顺序。
A
D
C
B
思考:根据定义画一个平行四边形,观察这个四边形,除了 “两组对边分别平行”以外,它的边、角之间有什么关系吗?度量一下,是不是和你的猜想一致?还有别的方法吗?
A
B
C
D
答:平行四边形的对边相等
平行四边形的对角相等
平行四边形的邻角互补
平行四边形的对边相等
平行四边形的对角相等
平行四边形的邻角互补
我们可以通过下面的动画来验证一下:
演 示
已知: ABCD
求证:AB=DC,BC=AD;
∠B=∠D,∠A=∠C.
A
B
C
D
证一证
1
2
3
4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
在△ABC和△CDA中
证明:连接AC
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∴AB=DC,BC=AD,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
即∠BAD=∠DCB
利用三角形全等得出全等三角形的对应边、对应角都相等,是证明线段相等、角相等的一种重要的方法。为此,我们通过添加辅助线,构造两个三角形,通过三角形全等进行证明。
平行四边形的性质
几何语言:
性质1:平行四边形的对边相等
性质2:平行四边形的对角相等
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC.(平行四边形的对边相等)
∵ 四边形ABCD是平行四边形
∴ ∠B=∠D,∠A=∠C.(平行四边形的对角相等).
随堂训练
判断题:(对的在括号内填“√”,错的填“×”)
(1)平行四边形两组对边分别平行且相等. ( )
(2)平行四边形的四个内角都相等. ( )
(3)平行四边形的相邻两个内角的和等于180°。( )
(4)如果平行四边形相邻两边长分别是2cm和3cm,那么周长10cm. ( )
(5)在平行四边形ABCD中,如果∠A=42°,那么∠B=48°. ( )
(6)在平行四边形ABCD中,如果∠A=35°, 那么∠C=145°. ( )
√
√
√
×
×
×
课堂小结
定义
两组对边分别平行的四边形
性质
平行四边形的对边相等
平行四边形的对角相等
平行
四边形
