2012【优化方案】精品练:物理教科必修1第1章第二节知能优化训练
文档属性
| 名称 | 2012【优化方案】精品练:物理教科必修1第1章第二节知能优化训练 |

|
|
| 格式 | zip | ||
| 文件大小 | 185.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2011-12-21 08:38:49 | ||
图片预览

文档简介
[学生用书 P11]
1.
图1-2-7
如图1-2-7所示,一物体沿三条不同的路径由A运动到B,下列关于它们的位移的说法中正确的是( )
A.沿Ⅰ较大
B.沿Ⅱ较大
C.沿Ⅲ较大
D.一样大
解析:选D.位移是用来表示质点位置变化的物理量,质点的始末位置确定后,位移矢量是唯一的,所以选D.
2.关于位移和路程,以下说法正确的是( )
①出租汽车按路程收费
②出租汽车按位移的大小收费
③在曲线运动中,同一运动过程的路程一定大于位移的绝对值(即大小)
④在直线运动中,位移就是路程
A.①③ B.②③
C.①④ D.②④
解析:选A.出租汽车按路程收费,曲线运动路径一定大于初末位置间线段的长度,所以路程一定大于位移大小,所以①③正确.只有单向直线运动中,位移大小等于路程,而位移是矢量,路程是标量,任何情况下位移也不能是路程.所以④错误.
3.关于矢量和标量,下列说法正确的是( )
A.标量只有正值,矢量可以取负值
B.标量和矢量无根本区别
C.标量和矢量,一个有大小无方向,一个有大小也有方向
D.以上说法均正确
解析:选C.由矢量和标量的定义可知,选项B和D错误,C正确.标量没有方向,但也可能有负值,比如温度,比0 ℃低时就出现负值.
4.
图1-2-8
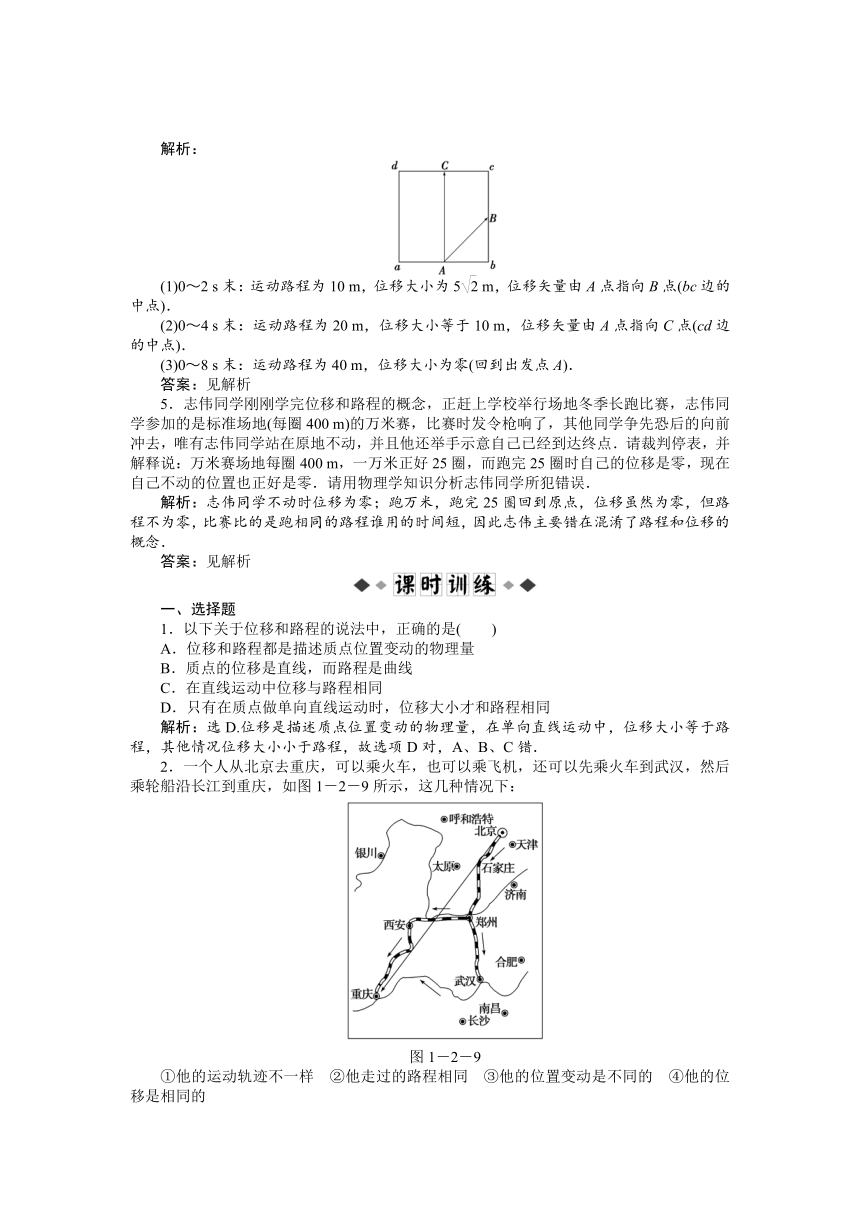
质点沿着图1-2-8所示的边长为10 m的正方形路线,从A点开始逆时针方向运动,每秒运动5 m.问:从开始运动时计时,到第2 s末、第4 s末、第8 s末的三段时间内,质点运动的路程和位移各多大?
解析:
(1)0~2 s末:运动路程为10 m,位移大小为5 m,位移矢量由A点指向B点(bc边的中点).
(2)0~4 s末:运动路程为20 m,位移大小等于10 m,位移矢量由A点指向C点(cd边的中点).
(3)0~8 s末:运动路程为40 m,位移大小为零(回到出发点A).
答案:见解析
5.志伟同学刚刚学完位移和路程的概念,正赶上学校举行场地冬季长跑比赛,志伟同学参加的是标准场地(每圈400 m)的万米赛,比赛时发令枪响了,其他同学争先恐后的向前冲去,唯有志伟同学站在原地不动,并且他还举手示意自己已经到达终点.请裁判停表,并解释说:万米赛场地每圈400 m,一万米正好25圈,而跑完25圈时自己的位移是零,现在自己不动的位置也正好是零.请用物理学知识分析志伟同学所犯错误.
解析:志伟同学不动时位移为零;跑万米,跑完25圈回到原点,位移虽然为零,但路程不为零,比赛比的是跑相同的路程谁用的时间短,因此志伟主要错在混淆了路程和位移的概念.
答案:见解析
一、选择题
1.以下关于位移和路程的说法中,正确的是( )
A.位移和路程都是描述质点位置变动的物理量
B.质点的位移是直线,而路程是曲线
C.在直线运动中位移与路程相同
D.只有在质点做单向直线运动时,位移大小才和路程相同
解析:选D.位移是描述质点位置变动的物理量,在单向直线运动中,位移大小等于路程,其他情况位移大小小于路程,故选项D对,A、B、C错.
2.一个人从北京去重庆,可以乘火车,也可以乘飞机,还可以先乘火车到武汉,然后乘轮船沿长江到重庆,如图1-2-9所示,这几种情况下:
图1-2-9
①他的运动轨迹不一样 ②他走过的路程相同 ③他的位置变动是不同的 ④他的位移是相同的
以上说法中正确的是( )
A.①② B.③④
C.①④ D.②③
解析:选C.这几种情况下,运动轨迹不同,路程也不同,但是他的始末位置相同,故位移相同,即位置变动相同,故选C.
3.
图1-2-10
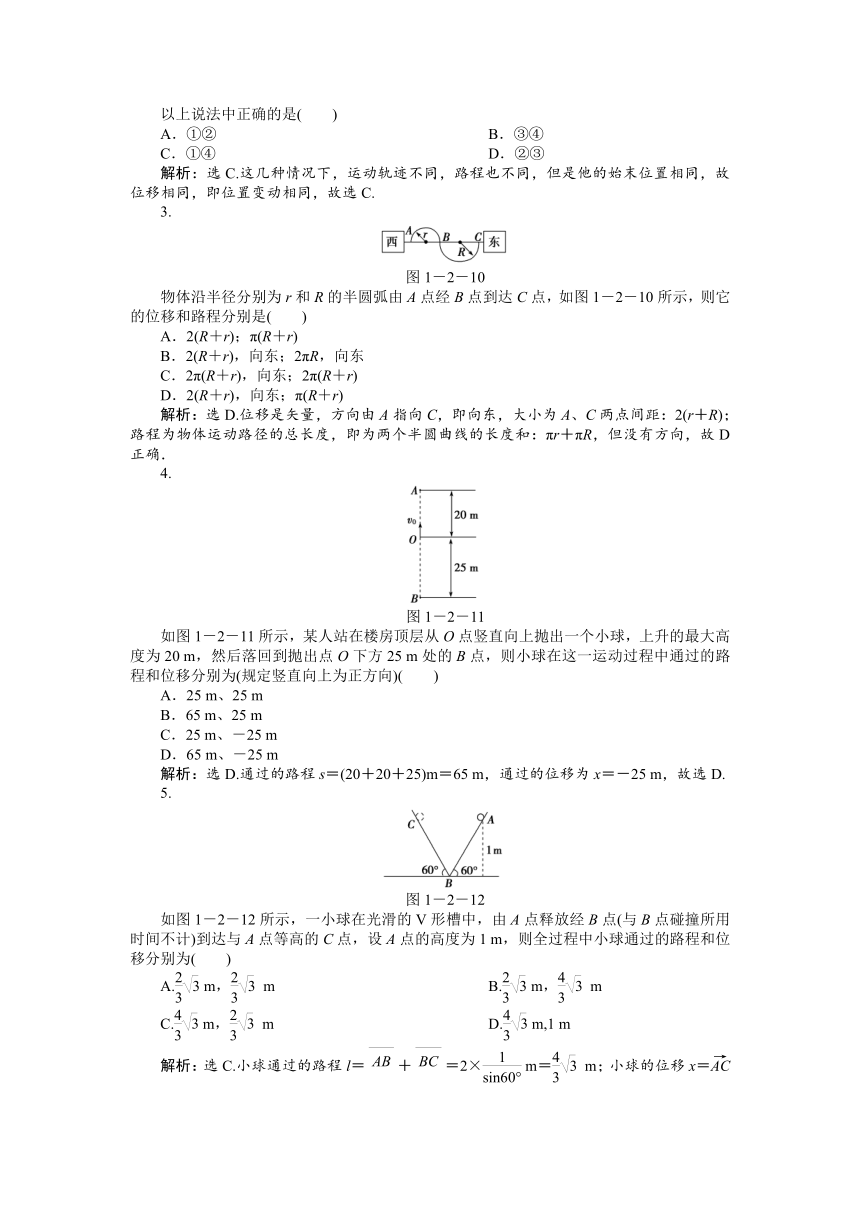
物体沿半径分别为r和R的半圆弧由A点经B点到达C点,如图1-2-10所示,则它的位移和路程分别是( )
A.2(R+r);π(R+r)
B.2(R+r),向东;2πR,向东
C.2π(R+r),向东;2π(R+r)
D.2(R+r),向东;π(R+r)
解析:选D.位移是矢量,方向由A指向C,即向东,大小为A、C两点间距:2(r+R);路程为物体运动路径的总长度,即为两个半圆曲线的长度和:πr+πR,但没有方向,故D正确.
4.
图1-2-11
如图1-2-11所示,某人站在楼房顶层从O点竖直向上抛出一个小球,上升的最大高度为20 m,然后落回到抛出点O下方25 m处的B点,则小球在这一运动过程中通过的路程和位移分别为(规定竖直向上为正方向)( )
A.25 m、25 m
B.65 m、25 m
C.25 m、-25 m
D.65 m、-25 m
解析:选D.通过的路程s=(20+20+25)m=65 m,通过的位移为x=-25 m,故选D.
5.
图1-2-12
如图1-2-12所示,一小球在光滑的V形槽中,由A点释放经B点(与B点碰撞所用时间不计)到达与A点等高的C点,设A点的高度为1 m,则全过程中小球通过的路程和位移分别为( )
A. m, m B. m, m
C. m, m D. m,1 m
解析:选C.小球通过的路程l=+=2× m= m;小球的位移x==2×cot60° m= m.故C正确.
6.
图1-2-13
将做直线运动的质点的位置变化描述在如图1-2-13所示的坐标轴上,x1、x2、…、xn-1、xn分别为质点在第1 s末、第2 s末、…、第(n-1) s末、第n s末的位置坐标,那么下列说法中正确的是( )
A.0~x2为第2 s内的位移
B.0~xn为第(n-1) s内的位移
C.x2~xn为第2 s内的位移
D.xn-1~xn为第n s内的位移
解析:选D.位移是起始位置到终止位置的有向线段,线段的长度表示位移的大小,线段的方向表示位移的方向,在辨别时间的基础上可以确定选项D正确.
7.关于位移和路程,下列说法中正确的是( )
A.在某段时间内,质点运动的位移为零,该质点不一定是静止的
B.在某段时间内,质点运动的路程为零,该质点不一定是静止的
C.在直线运动中,质点位移的大小一定等于其路程
D.在曲线运动中,质点位移的大小一定等于其路程
解析:选A.因为当物体由某位置运动到其他位置后又回到原来的位置时位移为零,路程不为零,质点不是静止,故选项A对B错;在直线运动中,如果运动过程中有往返,则位移的大小也不等于路程,而在曲线运动中位移一定小于路程,故选项C、D都不对.
8.某人沿着半径为R的水平圆周跑道跑了1.75圈时,他的( )
A.路程和位移的大小均为3.5πR
B.路程和位移的大小均为R
C.路程为3.5πR、位移的大小为R
D.路程为0.5πR、位移的大小为R
解析:选C.他的路程为1.75×2πR=3.5πR;位移为初末位置间的有向线段,即R,所以C项正确.
图1-2-14
9.如图1-2-14所示是一边长为10 cm的实心立方体木块,一只昆虫从A点爬到G点.下列说法正确的是( )
A.该昆虫的路程有若干种可能性,其中最短路程为(10+10) cm
B.该昆虫的位移为10 cm
C.该昆虫的路程有若干种可能性,其中最短路程为10 cm
D.该昆虫的位移为10 cm
解析:
选CD.昆虫只能沿木块表面从A点到G点,其运动轨迹可以有各种不同的情况,但是,其起点和终点是相同的,即位移相同(为立方体对角线的长度10 cm);其最短路程分析可知:应该从相邻的两个面到达G才可能最短,我们可以把面AEFD和CDFG展开(如图),然后连接A与G,AIG的长度就是最短路程,为10 cm.
二、非选择题
10.
图1-2-15
如图1-2-15所示,某物体沿半径为40 cm的圆轨道运动,某时刻从A点出发,沿弧ACB经过一段时间到达B点(内接△ABC为等边三角形).求物体在这段时间里通过的路程与位移大小.
解析:物体走过的圆心角的大小为240°,即物体走过了圆,所以物体的路程为×2πr= cm.
而位移的大小为从A到B的有向线段的长度,
即x=40 cm,方向由A到B.
答案: cm 40 cm
11.某人从水平地面上的A点出发,先向正东走了40 m到达B点,接着又向正北方向走了30 m到达C点,求:
(1)这两个过程中人的位移的大小和方向;
(2)整个过程中人的路程和位移.
解析:
(1)第一个过程中从A到B,位移大小为:
x1=A=40 m,方向向东
第二过程中从B到C,位移大小为:
x2=B=30 m,方向向北.
(2)整个过程中的路程
s=A+=40 m+30 m=70 m
总位移大小为:x=A=
= m=50 m
方向:tan α== ,所以α=37°
即东偏北37°.
答案:见解析
12.一支长150 m的队伍匀速前进,通信员从队尾前进300 m后赶到队首,传达命令后立即返回,当通信员回到队尾时,队伍已前进了200 m,则在此全过程中,通信员的位移和路程分别是多少?
解析:
通信员在此全程中的位移与队伍的位移相同.
所以x=200 m
通信员的运动情况为A→B→C
由题意知:AB=300 m BC=300 m-200 m=100 m
所以总路程为s=300 m+100 m=400 m.
答案:200 m 400 m
1.
图1-2-7
如图1-2-7所示,一物体沿三条不同的路径由A运动到B,下列关于它们的位移的说法中正确的是( )
A.沿Ⅰ较大
B.沿Ⅱ较大
C.沿Ⅲ较大
D.一样大
解析:选D.位移是用来表示质点位置变化的物理量,质点的始末位置确定后,位移矢量是唯一的,所以选D.
2.关于位移和路程,以下说法正确的是( )
①出租汽车按路程收费
②出租汽车按位移的大小收费
③在曲线运动中,同一运动过程的路程一定大于位移的绝对值(即大小)
④在直线运动中,位移就是路程
A.①③ B.②③
C.①④ D.②④
解析:选A.出租汽车按路程收费,曲线运动路径一定大于初末位置间线段的长度,所以路程一定大于位移大小,所以①③正确.只有单向直线运动中,位移大小等于路程,而位移是矢量,路程是标量,任何情况下位移也不能是路程.所以④错误.
3.关于矢量和标量,下列说法正确的是( )
A.标量只有正值,矢量可以取负值
B.标量和矢量无根本区别
C.标量和矢量,一个有大小无方向,一个有大小也有方向
D.以上说法均正确
解析:选C.由矢量和标量的定义可知,选项B和D错误,C正确.标量没有方向,但也可能有负值,比如温度,比0 ℃低时就出现负值.
4.
图1-2-8
质点沿着图1-2-8所示的边长为10 m的正方形路线,从A点开始逆时针方向运动,每秒运动5 m.问:从开始运动时计时,到第2 s末、第4 s末、第8 s末的三段时间内,质点运动的路程和位移各多大?
解析:
(1)0~2 s末:运动路程为10 m,位移大小为5 m,位移矢量由A点指向B点(bc边的中点).
(2)0~4 s末:运动路程为20 m,位移大小等于10 m,位移矢量由A点指向C点(cd边的中点).
(3)0~8 s末:运动路程为40 m,位移大小为零(回到出发点A).
答案:见解析
5.志伟同学刚刚学完位移和路程的概念,正赶上学校举行场地冬季长跑比赛,志伟同学参加的是标准场地(每圈400 m)的万米赛,比赛时发令枪响了,其他同学争先恐后的向前冲去,唯有志伟同学站在原地不动,并且他还举手示意自己已经到达终点.请裁判停表,并解释说:万米赛场地每圈400 m,一万米正好25圈,而跑完25圈时自己的位移是零,现在自己不动的位置也正好是零.请用物理学知识分析志伟同学所犯错误.
解析:志伟同学不动时位移为零;跑万米,跑完25圈回到原点,位移虽然为零,但路程不为零,比赛比的是跑相同的路程谁用的时间短,因此志伟主要错在混淆了路程和位移的概念.
答案:见解析
一、选择题
1.以下关于位移和路程的说法中,正确的是( )
A.位移和路程都是描述质点位置变动的物理量
B.质点的位移是直线,而路程是曲线
C.在直线运动中位移与路程相同
D.只有在质点做单向直线运动时,位移大小才和路程相同
解析:选D.位移是描述质点位置变动的物理量,在单向直线运动中,位移大小等于路程,其他情况位移大小小于路程,故选项D对,A、B、C错.
2.一个人从北京去重庆,可以乘火车,也可以乘飞机,还可以先乘火车到武汉,然后乘轮船沿长江到重庆,如图1-2-9所示,这几种情况下:
图1-2-9
①他的运动轨迹不一样 ②他走过的路程相同 ③他的位置变动是不同的 ④他的位移是相同的
以上说法中正确的是( )
A.①② B.③④
C.①④ D.②③
解析:选C.这几种情况下,运动轨迹不同,路程也不同,但是他的始末位置相同,故位移相同,即位置变动相同,故选C.
3.
图1-2-10
物体沿半径分别为r和R的半圆弧由A点经B点到达C点,如图1-2-10所示,则它的位移和路程分别是( )
A.2(R+r);π(R+r)
B.2(R+r),向东;2πR,向东
C.2π(R+r),向东;2π(R+r)
D.2(R+r),向东;π(R+r)
解析:选D.位移是矢量,方向由A指向C,即向东,大小为A、C两点间距:2(r+R);路程为物体运动路径的总长度,即为两个半圆曲线的长度和:πr+πR,但没有方向,故D正确.
4.
图1-2-11
如图1-2-11所示,某人站在楼房顶层从O点竖直向上抛出一个小球,上升的最大高度为20 m,然后落回到抛出点O下方25 m处的B点,则小球在这一运动过程中通过的路程和位移分别为(规定竖直向上为正方向)( )
A.25 m、25 m
B.65 m、25 m
C.25 m、-25 m
D.65 m、-25 m
解析:选D.通过的路程s=(20+20+25)m=65 m,通过的位移为x=-25 m,故选D.
5.
图1-2-12
如图1-2-12所示,一小球在光滑的V形槽中,由A点释放经B点(与B点碰撞所用时间不计)到达与A点等高的C点,设A点的高度为1 m,则全过程中小球通过的路程和位移分别为( )
A. m, m B. m, m
C. m, m D. m,1 m
解析:选C.小球通过的路程l=+=2× m= m;小球的位移x==2×cot60° m= m.故C正确.
6.
图1-2-13
将做直线运动的质点的位置变化描述在如图1-2-13所示的坐标轴上,x1、x2、…、xn-1、xn分别为质点在第1 s末、第2 s末、…、第(n-1) s末、第n s末的位置坐标,那么下列说法中正确的是( )
A.0~x2为第2 s内的位移
B.0~xn为第(n-1) s内的位移
C.x2~xn为第2 s内的位移
D.xn-1~xn为第n s内的位移
解析:选D.位移是起始位置到终止位置的有向线段,线段的长度表示位移的大小,线段的方向表示位移的方向,在辨别时间的基础上可以确定选项D正确.
7.关于位移和路程,下列说法中正确的是( )
A.在某段时间内,质点运动的位移为零,该质点不一定是静止的
B.在某段时间内,质点运动的路程为零,该质点不一定是静止的
C.在直线运动中,质点位移的大小一定等于其路程
D.在曲线运动中,质点位移的大小一定等于其路程
解析:选A.因为当物体由某位置运动到其他位置后又回到原来的位置时位移为零,路程不为零,质点不是静止,故选项A对B错;在直线运动中,如果运动过程中有往返,则位移的大小也不等于路程,而在曲线运动中位移一定小于路程,故选项C、D都不对.
8.某人沿着半径为R的水平圆周跑道跑了1.75圈时,他的( )
A.路程和位移的大小均为3.5πR
B.路程和位移的大小均为R
C.路程为3.5πR、位移的大小为R
D.路程为0.5πR、位移的大小为R
解析:选C.他的路程为1.75×2πR=3.5πR;位移为初末位置间的有向线段,即R,所以C项正确.
图1-2-14
9.如图1-2-14所示是一边长为10 cm的实心立方体木块,一只昆虫从A点爬到G点.下列说法正确的是( )
A.该昆虫的路程有若干种可能性,其中最短路程为(10+10) cm
B.该昆虫的位移为10 cm
C.该昆虫的路程有若干种可能性,其中最短路程为10 cm
D.该昆虫的位移为10 cm
解析:
选CD.昆虫只能沿木块表面从A点到G点,其运动轨迹可以有各种不同的情况,但是,其起点和终点是相同的,即位移相同(为立方体对角线的长度10 cm);其最短路程分析可知:应该从相邻的两个面到达G才可能最短,我们可以把面AEFD和CDFG展开(如图),然后连接A与G,AIG的长度就是最短路程,为10 cm.
二、非选择题
10.
图1-2-15
如图1-2-15所示,某物体沿半径为40 cm的圆轨道运动,某时刻从A点出发,沿弧ACB经过一段时间到达B点(内接△ABC为等边三角形).求物体在这段时间里通过的路程与位移大小.
解析:物体走过的圆心角的大小为240°,即物体走过了圆,所以物体的路程为×2πr= cm.
而位移的大小为从A到B的有向线段的长度,
即x=40 cm,方向由A到B.
答案: cm 40 cm
11.某人从水平地面上的A点出发,先向正东走了40 m到达B点,接着又向正北方向走了30 m到达C点,求:
(1)这两个过程中人的位移的大小和方向;
(2)整个过程中人的路程和位移.
解析:
(1)第一个过程中从A到B,位移大小为:
x1=A=40 m,方向向东
第二过程中从B到C,位移大小为:
x2=B=30 m,方向向北.
(2)整个过程中的路程
s=A+=40 m+30 m=70 m
总位移大小为:x=A=
= m=50 m
方向:tan α== ,所以α=37°
即东偏北37°.
答案:见解析
12.一支长150 m的队伍匀速前进,通信员从队尾前进300 m后赶到队首,传达命令后立即返回,当通信员回到队尾时,队伍已前进了200 m,则在此全过程中,通信员的位移和路程分别是多少?
解析:
通信员在此全程中的位移与队伍的位移相同.
所以x=200 m
通信员的运动情况为A→B→C
由题意知:AB=300 m BC=300 m-200 m=100 m
所以总路程为s=300 m+100 m=400 m.
答案:200 m 400 m
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
