湘教版 八年级数学下册 第1章 直角三角形 1.2.1勾股定理 同步练习 (Word版 含答案)
文档属性
| 名称 | 湘教版 八年级数学下册 第1章 直角三角形 1.2.1勾股定理 同步练习 (Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 325.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 11:34:29 | ||
图片预览

文档简介
1.2.1勾股定理
1.若一个直角三角形的两直角边的长分别为a,b,斜边长为c,则下列关于a,b,c的关系式中不正确的是( )
A.b2=c2-a2 B.a2=c2-b2
C.b2=a2-c2 D.c2=a2+b2
2.【中考·滨州】在直角三角形中,若勾为3,股为4,则弦为( )
A.5 B.6 C.7 D.8
3.已知一个直角三角形的两条边长分别为8和15,则第三条边长为( )
A.17 B.
C.或17 D.不确定
4.【中考·毕节】如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为( )
A. B.3 C. D.5
5.【中考·陕西】如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为( )
A. B. C. D.
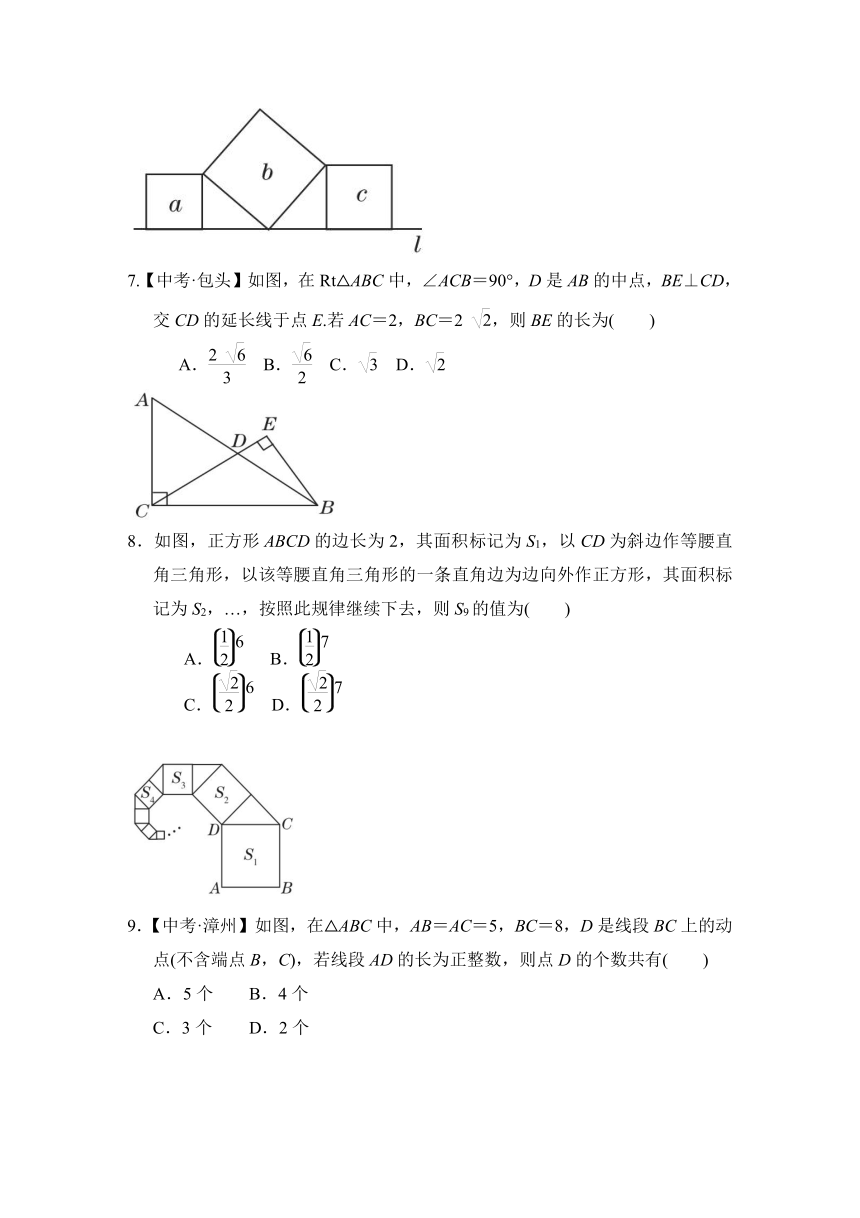
6.如图,直线l上有三个正方形a,b,c,若a,c的面积分别为3和4,则b的面积为( D )
A.3 B.4 C.5 D.7
7.【中考·包头】如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,BE⊥CD,交CD的延长线于点E.若AC=2,BC=2 ,则BE的长为( )
A. B. C. D.
8.如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…,按照此规律继续下去,则S9的值为( )
A. B.
C. D.
9.【中考·漳州】如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B,C),若线段AD的长为正整数,则点D的个数共有( )
A.5个 B.4个
C.3个 D.2个
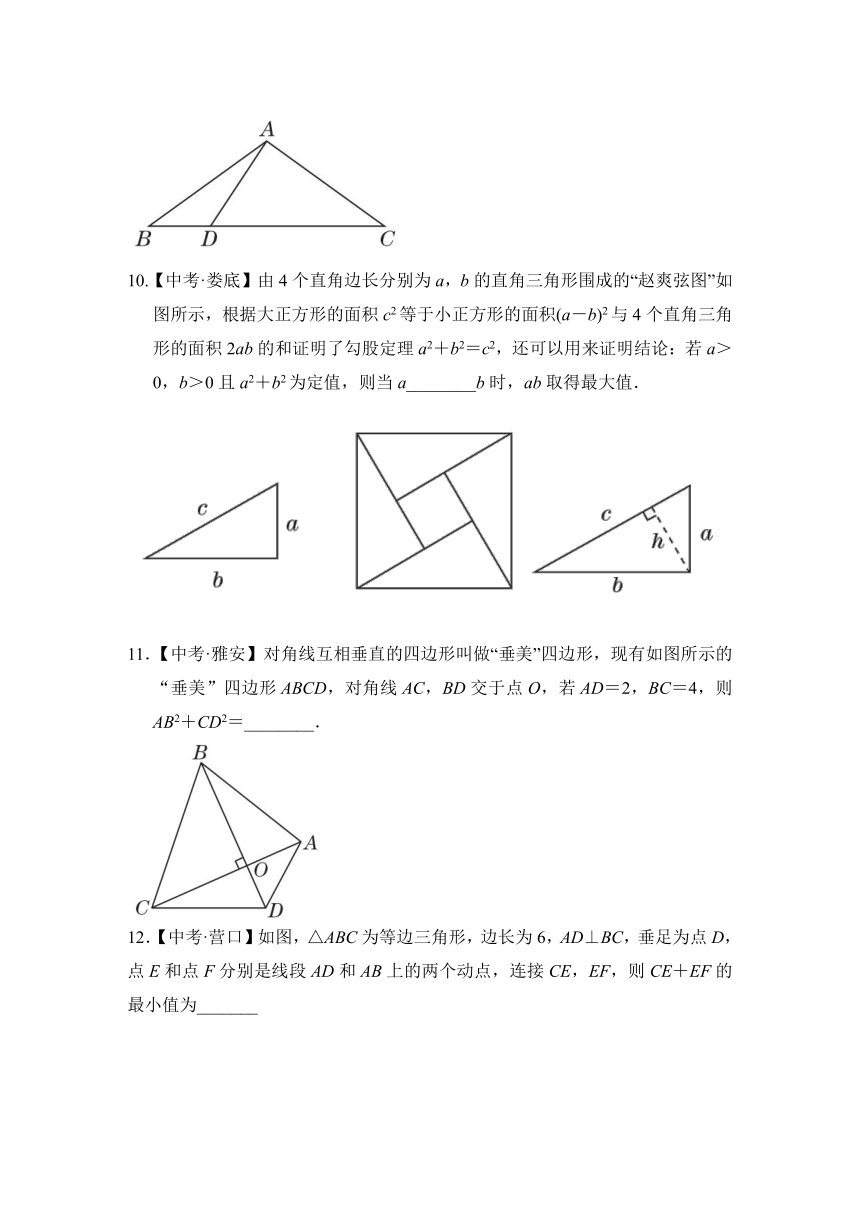
10.【中考·娄底】由4个直角边长分别为a,b的直角三角形围成的“赵爽弦图”如图所示,根据大正方形的面积c2等于小正方形的面积(a-b)2与4个直角三角形的面积2ab的和证明了勾股定理a2+b2=c2,还可以用来证明结论:若a>0,b>0且a2+b2为定值,则当a________b时,ab取得最大值.
11.【中考·雅安】对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC,BD交于点O,若AD=2,BC=4,则AB2+CD2=________.
12.【中考·营口】如图,△ABC为等边三角形,边长为6,AD⊥BC,垂足为点D,点E和点F分别是线段AD和AB上的两个动点,连接CE,EF,则CE+EF的最小值为_______
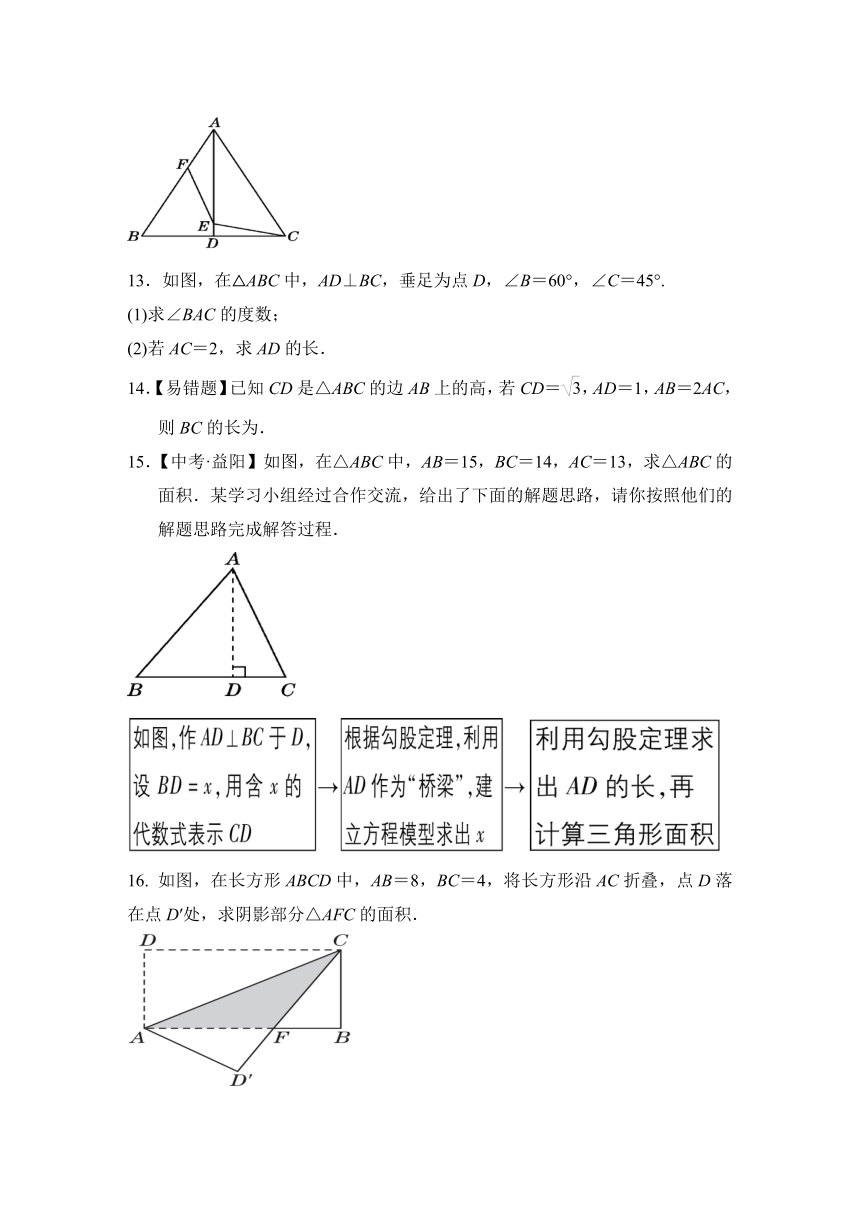
13.如图,在△ABC中,AD⊥BC,垂足为点D,∠B=60°,∠C=45°.
(1)求∠BAC的度数;
(2)若AC=2,求AD的长.
14.【易错题】已知CD是△ABC的边AB上的高,若CD=,AD=1,AB=2AC,则BC的长为.
15.【中考·益阳】如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
如图,在长方形ABCD中,AB=8,BC=4,将长方形沿AC折叠,点D落在点D′处,求阴影部分△AFC的面积.
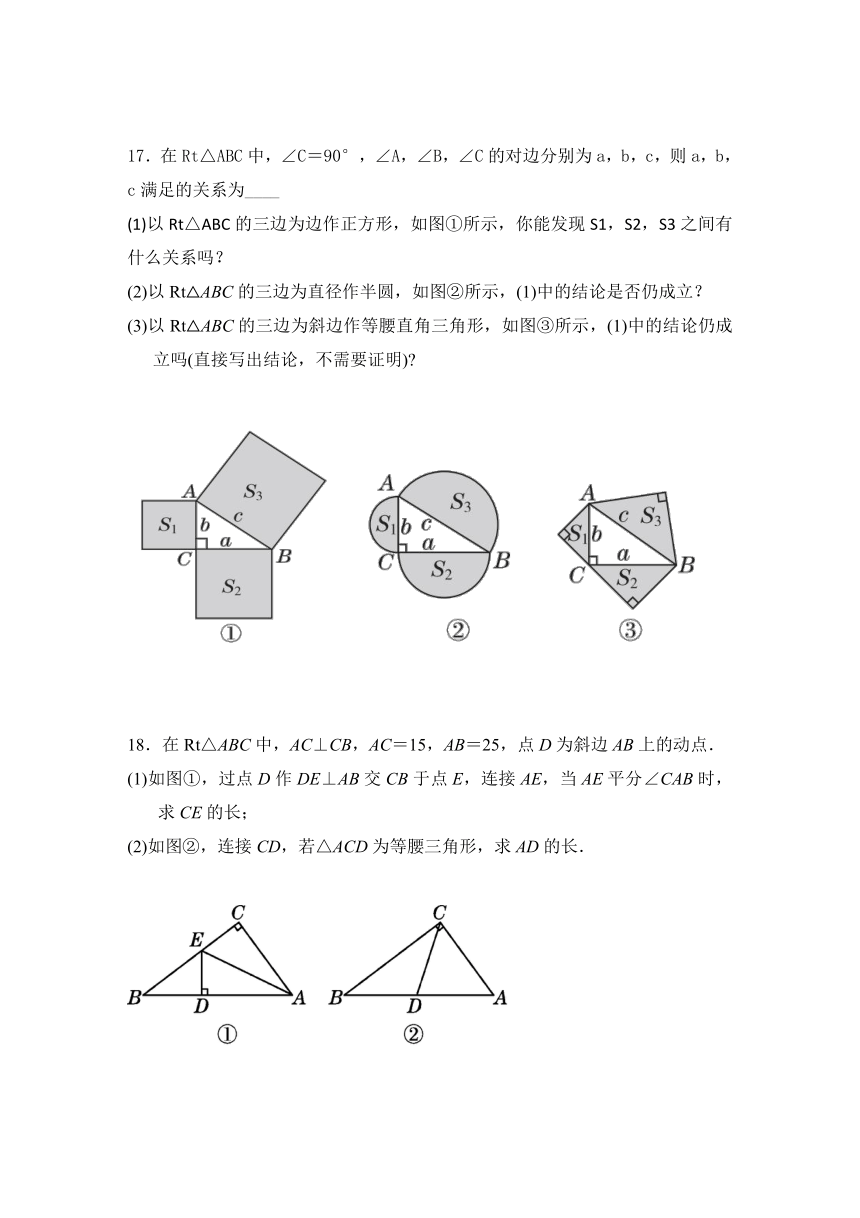
17.在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,则a,b,c满足的关系为____
(1)以Rt△ABC的三边为边作正方形,如图①所示,你能发现S1,S2,S3之间有什么关系吗?
(2)以Rt△ABC的三边为直径作半圆,如图②所示,(1)中的结论是否仍成立?
(3)以Rt△ABC的三边为斜边作等腰直角三角形,如图③所示,(1)中的结论仍成立吗(直接写出结论,不需要证明)?
18.在Rt△ABC中,AC⊥CB,AC=15,AB=25,点D为斜边AB上的动点.
(1)如图①,过点D作DE⊥AB交CB于点E,连接AE,当AE平分∠CAB时,求CE的长;
(2)如图②,连接CD,若△ACD为等腰三角形,求AD的长.
1.2.1勾股定理
1.若一个直角三角形的两直角边的长分别为a,b,斜边长为c,则下列关于a,b,c的关系式中不正确的是( C )
A.b2=c2-a2 B.a2=c2-b2
C.b2=a2-c2 D.c2=a2+b2
2.【中考·滨州】在直角三角形中,若勾为3,股为4,则弦为( A )
A.5 B.6 C.7 D.8
3.已知一个直角三角形的两条边长分别为8和15,则第三条边长为( C )
A.17 B.
C.或17 D.不确定
4.【中考·毕节】如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为( B )
A. B.3 C. D.5
5.【中考·陕西】如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为( D )
A. B. C. D.
【点拨】由勾股定理得AC==.
∵S△ABC=3×3-×1×2-×1×3-×2×3=,
∴AC·BD=,∴·BD=7,∴BD=.
6.如图,直线l上有三个正方形a,b,c,若a,c的面积分别为3和4,则b的面积为( D )
A.3 B.4 C.5 D.7
7.【中考·包头】如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,BE⊥CD,交CD的延长线于点E.若AC=2,BC=2 ,则BE的长为( A )
A. B. C. D.
【点拨】在Rt△ABC中,∠ACB=90°,AC=2,BC=2,由勾股定理得AB===2 .∵D是AB的中点,∴BD=CD=.设DE=x,由勾股定理得()2-x2=(2 )2-(+x)2,解得x=,
∴在Rt△BED中,BE===.
8.如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…,按照此规律继续下去,则S9的值为( A )
A. B.
C. D.
9.【中考·漳州】如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B,C),若线段AD的长为正整数,则点D的个数共有( C )
A.5个 B.4个
C.3个 D.2个
【点拨】过A作AE⊥BC,垂足为E,
∵AB=AC,∴EC=BE=BC=4,∴AE==3.
∵D是线段BC上的动点(不含端点B,C),∴3≤AD<5,
∵AD的长为正整数,∴AD=3或AD=4,
∴点D的个数共有3个.
此题易因没看清题意,得出3≤AD≤5,从而得到错误答案A.
10.【中考·娄底】由4个直角边长分别为a,b的直角三角形围成的“赵爽弦图”如图所示,根据大正方形的面积c2等于小正方形的面积(a-b)2与4个直角三角形的面积2ab的和证明了勾股定理a2+b2=c2,还可以用来证明结论:若a>0,b>0且a2+b2为定值,则当a___=_____b时,ab取得最大值.
【点拨】如图,在直角三角形中,两直角边长为a,b,斜边长为c,则a2+b2=c2.作直角三角形斜边上的高h,易知ab=ch,即ab=ch.
∵(a-b)2≥0,∴a2+b2-2ab≥0.又∵a2+b2=c2,a2+b2为定值,
∴ab≤,∴ab的最大值为.
当ab取最大值时,ab==ch,∴h=.要想使直角三角形中斜边上的高等于斜边的一半,则此三角形为等腰直角三角形,即a=b.
11.【中考·雅安】对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC,BD交于点O,若AD=2,BC=4,则AB2+CD2=__20______.
12.【中考·营口】如图,△ABC为等边三角形,边长为6,AD⊥BC,垂足为点D,点E和点F分别是线段AD和AB上的两个动点,连接CE,EF,则CE+EF的最小值为__3 _____
13.如图,在△ABC中,AD⊥BC,垂足为点D,∠B=60°,∠C=45°.
(1)求∠BAC的度数;
(2)若AC=2,求AD的长.
解:(1)∵∠C=45°,∠B=60°,
∴∠BAC=180°-60°-45°=75°.
(2):∵AD⊥BC,∴∠ADC=90°.
又∵∠C=45°,∴∠DAC=45°=∠C,
∴AD=CD.
在Rt△ACD中,∵AC=2,
∴AD2+DC2=22.∴AD=.
14.【易错题】已知CD是△ABC的边AB上的高,若CD=,AD=1,AB=2AC,则BC的长为.
【点拨】分两种情况讨论:
当CD在△ABC内部时,如图①,
∵CD⊥AB,∴∠CDA=90°. ∵CD=,AD=1,∴AC=2.
∵AB=2AC,∴AB=4,∴BD=4-1=3,
∴BC==2 .
②当CD在△ABC外部时,如图②,同理得AC=2,AB=4,
∴BD=4+1=5,∴BC==2 .
综上所述,BC的长为2 或2 .
15.【中考·益阳】如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
解:作AD⊥BC于D,设BD=x,则CD=14-x,
根据勾股定理,得AD2=AB2-BD2=152-x2,
AD2=AC2-CD2=132-(14-x)2,
∴152-x2=132-(14-x)2,解得x=9.
∴AD2=AB2-BD2=152-92=144. ∴AD=12.
∴S△ABC=BC·AD=×14×12=84.
如图,在长方形ABCD中,AB=8,BC=4,将长方形沿AC折叠,点D落在点D′处,求阴影部分△AFC的面积.
解:由题意可知∠D′=∠D=∠B=90°,AD′=AD=BC=4.又∠AFD′=∠CFB,∴△AFD′≌△CFB,∴D′F=BF.
设D′F=BF=x,则AF=8-x,
在Rt△AFD′中,(8-x)2=x2+42,解得x=3,
∴AF=8-3=5,∴S△AFC=AF·BC=10.
17.在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,则a,b,c满足的关系为_____a2+b2=c2________
(1)以Rt△ABC的三边为边作正方形,如图①所示,你能发现S1,S2,S3之间有什么关系吗?
(2)以Rt△ABC的三边为直径作半圆,如图②所示,(1)中的结论是否仍成立?
(3)以Rt△ABC的三边为斜边作等腰直角三角形,如图③所示,(1)中的结论仍成立吗(直接写出结论,不需要证明)?
解:(1)由题意得S1=b2,S2=a2,S3=c2.
∵a2+b2=c2,∴S1+S2=S3.
(2):仍成立.理由如下:易得S1=·b2,S2=·a2,S3=·c2,
∵a2+b2=c2,∴S1+S2=S3.
即(1)中的结论仍成立.
:S1+S2=S3仍成立.
18.在Rt△ABC中,AC⊥CB,AC=15,AB=25,点D为斜边AB上的动点.
(1)如图①,过点D作DE⊥AB交CB于点E,连接AE,当AE平分∠CAB时,求CE的长;
(2)如图②,连接CD,若△ACD为等腰三角形,求AD的长.
解:(1)∵AC⊥CB,AC=15,AB=25,∴BC=20.
∵AE平分∠CAB,∴∠EAC=∠EAD.
∵AC⊥CB,DE⊥AB,∴∠ECA=∠EDA=90°.
又∵AE=AE,∴△ACE≌△ADE(AAS),
∴CE=DE,AC=AD=15.∴BD=25-15=10.
设CE=DE=x,则BE=20-x,
在Rt△BED中,x2+102=(20-x)2,∴x=7.5,∴CE=7.5.
(2):①当AD=AC时,△ACD为等腰三角形.
∵AC=15,∴AD=AC=15.
②当CD=AD时,△ACD为等腰三角形.
∵CD=AD,∴∠DCA=∠CAD.
∵AC⊥CB,∴∠CAB+∠B=90°,∠DCA+∠BCD=90°,
∴∠B=∠BCD,∴BD=CD,∴AD=BD=12.5.
③当CD=AC时,△ACD为等腰三角形,
如图,过点C作CH⊥BA于点H,易知AB·CH=AC·BC.
∵AC=15,BC=20,AB=25,∴CH=12.
∴在Rt△ACH中,AH==9.
∵CD=AC,CH⊥BA,∴DH=HA=9,
∴AD=18.
综上,AD的长为15或12.5或18.
1.若一个直角三角形的两直角边的长分别为a,b,斜边长为c,则下列关于a,b,c的关系式中不正确的是( )
A.b2=c2-a2 B.a2=c2-b2
C.b2=a2-c2 D.c2=a2+b2
2.【中考·滨州】在直角三角形中,若勾为3,股为4,则弦为( )
A.5 B.6 C.7 D.8
3.已知一个直角三角形的两条边长分别为8和15,则第三条边长为( )
A.17 B.
C.或17 D.不确定
4.【中考·毕节】如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为( )
A. B.3 C. D.5
5.【中考·陕西】如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为( )
A. B. C. D.
6.如图,直线l上有三个正方形a,b,c,若a,c的面积分别为3和4,则b的面积为( D )
A.3 B.4 C.5 D.7
7.【中考·包头】如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,BE⊥CD,交CD的延长线于点E.若AC=2,BC=2 ,则BE的长为( )
A. B. C. D.
8.如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…,按照此规律继续下去,则S9的值为( )
A. B.
C. D.
9.【中考·漳州】如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B,C),若线段AD的长为正整数,则点D的个数共有( )
A.5个 B.4个
C.3个 D.2个
10.【中考·娄底】由4个直角边长分别为a,b的直角三角形围成的“赵爽弦图”如图所示,根据大正方形的面积c2等于小正方形的面积(a-b)2与4个直角三角形的面积2ab的和证明了勾股定理a2+b2=c2,还可以用来证明结论:若a>0,b>0且a2+b2为定值,则当a________b时,ab取得最大值.
11.【中考·雅安】对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC,BD交于点O,若AD=2,BC=4,则AB2+CD2=________.
12.【中考·营口】如图,△ABC为等边三角形,边长为6,AD⊥BC,垂足为点D,点E和点F分别是线段AD和AB上的两个动点,连接CE,EF,则CE+EF的最小值为_______
13.如图,在△ABC中,AD⊥BC,垂足为点D,∠B=60°,∠C=45°.
(1)求∠BAC的度数;
(2)若AC=2,求AD的长.
14.【易错题】已知CD是△ABC的边AB上的高,若CD=,AD=1,AB=2AC,则BC的长为.
15.【中考·益阳】如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
如图,在长方形ABCD中,AB=8,BC=4,将长方形沿AC折叠,点D落在点D′处,求阴影部分△AFC的面积.
17.在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,则a,b,c满足的关系为____
(1)以Rt△ABC的三边为边作正方形,如图①所示,你能发现S1,S2,S3之间有什么关系吗?
(2)以Rt△ABC的三边为直径作半圆,如图②所示,(1)中的结论是否仍成立?
(3)以Rt△ABC的三边为斜边作等腰直角三角形,如图③所示,(1)中的结论仍成立吗(直接写出结论,不需要证明)?
18.在Rt△ABC中,AC⊥CB,AC=15,AB=25,点D为斜边AB上的动点.
(1)如图①,过点D作DE⊥AB交CB于点E,连接AE,当AE平分∠CAB时,求CE的长;
(2)如图②,连接CD,若△ACD为等腰三角形,求AD的长.
1.2.1勾股定理
1.若一个直角三角形的两直角边的长分别为a,b,斜边长为c,则下列关于a,b,c的关系式中不正确的是( C )
A.b2=c2-a2 B.a2=c2-b2
C.b2=a2-c2 D.c2=a2+b2
2.【中考·滨州】在直角三角形中,若勾为3,股为4,则弦为( A )
A.5 B.6 C.7 D.8
3.已知一个直角三角形的两条边长分别为8和15,则第三条边长为( C )
A.17 B.
C.或17 D.不确定
4.【中考·毕节】如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为( B )
A. B.3 C. D.5
5.【中考·陕西】如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为( D )
A. B. C. D.
【点拨】由勾股定理得AC==.
∵S△ABC=3×3-×1×2-×1×3-×2×3=,
∴AC·BD=,∴·BD=7,∴BD=.
6.如图,直线l上有三个正方形a,b,c,若a,c的面积分别为3和4,则b的面积为( D )
A.3 B.4 C.5 D.7
7.【中考·包头】如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,BE⊥CD,交CD的延长线于点E.若AC=2,BC=2 ,则BE的长为( A )
A. B. C. D.
【点拨】在Rt△ABC中,∠ACB=90°,AC=2,BC=2,由勾股定理得AB===2 .∵D是AB的中点,∴BD=CD=.设DE=x,由勾股定理得()2-x2=(2 )2-(+x)2,解得x=,
∴在Rt△BED中,BE===.
8.如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…,按照此规律继续下去,则S9的值为( A )
A. B.
C. D.
9.【中考·漳州】如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B,C),若线段AD的长为正整数,则点D的个数共有( C )
A.5个 B.4个
C.3个 D.2个
【点拨】过A作AE⊥BC,垂足为E,
∵AB=AC,∴EC=BE=BC=4,∴AE==3.
∵D是线段BC上的动点(不含端点B,C),∴3≤AD<5,
∵AD的长为正整数,∴AD=3或AD=4,
∴点D的个数共有3个.
此题易因没看清题意,得出3≤AD≤5,从而得到错误答案A.
10.【中考·娄底】由4个直角边长分别为a,b的直角三角形围成的“赵爽弦图”如图所示,根据大正方形的面积c2等于小正方形的面积(a-b)2与4个直角三角形的面积2ab的和证明了勾股定理a2+b2=c2,还可以用来证明结论:若a>0,b>0且a2+b2为定值,则当a___=_____b时,ab取得最大值.
【点拨】如图,在直角三角形中,两直角边长为a,b,斜边长为c,则a2+b2=c2.作直角三角形斜边上的高h,易知ab=ch,即ab=ch.
∵(a-b)2≥0,∴a2+b2-2ab≥0.又∵a2+b2=c2,a2+b2为定值,
∴ab≤,∴ab的最大值为.
当ab取最大值时,ab==ch,∴h=.要想使直角三角形中斜边上的高等于斜边的一半,则此三角形为等腰直角三角形,即a=b.
11.【中考·雅安】对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC,BD交于点O,若AD=2,BC=4,则AB2+CD2=__20______.
12.【中考·营口】如图,△ABC为等边三角形,边长为6,AD⊥BC,垂足为点D,点E和点F分别是线段AD和AB上的两个动点,连接CE,EF,则CE+EF的最小值为__3 _____
13.如图,在△ABC中,AD⊥BC,垂足为点D,∠B=60°,∠C=45°.
(1)求∠BAC的度数;
(2)若AC=2,求AD的长.
解:(1)∵∠C=45°,∠B=60°,
∴∠BAC=180°-60°-45°=75°.
(2):∵AD⊥BC,∴∠ADC=90°.
又∵∠C=45°,∴∠DAC=45°=∠C,
∴AD=CD.
在Rt△ACD中,∵AC=2,
∴AD2+DC2=22.∴AD=.
14.【易错题】已知CD是△ABC的边AB上的高,若CD=,AD=1,AB=2AC,则BC的长为.
【点拨】分两种情况讨论:
当CD在△ABC内部时,如图①,
∵CD⊥AB,∴∠CDA=90°. ∵CD=,AD=1,∴AC=2.
∵AB=2AC,∴AB=4,∴BD=4-1=3,
∴BC==2 .
②当CD在△ABC外部时,如图②,同理得AC=2,AB=4,
∴BD=4+1=5,∴BC==2 .
综上所述,BC的长为2 或2 .
15.【中考·益阳】如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
解:作AD⊥BC于D,设BD=x,则CD=14-x,
根据勾股定理,得AD2=AB2-BD2=152-x2,
AD2=AC2-CD2=132-(14-x)2,
∴152-x2=132-(14-x)2,解得x=9.
∴AD2=AB2-BD2=152-92=144. ∴AD=12.
∴S△ABC=BC·AD=×14×12=84.
如图,在长方形ABCD中,AB=8,BC=4,将长方形沿AC折叠,点D落在点D′处,求阴影部分△AFC的面积.
解:由题意可知∠D′=∠D=∠B=90°,AD′=AD=BC=4.又∠AFD′=∠CFB,∴△AFD′≌△CFB,∴D′F=BF.
设D′F=BF=x,则AF=8-x,
在Rt△AFD′中,(8-x)2=x2+42,解得x=3,
∴AF=8-3=5,∴S△AFC=AF·BC=10.
17.在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,则a,b,c满足的关系为_____a2+b2=c2________
(1)以Rt△ABC的三边为边作正方形,如图①所示,你能发现S1,S2,S3之间有什么关系吗?
(2)以Rt△ABC的三边为直径作半圆,如图②所示,(1)中的结论是否仍成立?
(3)以Rt△ABC的三边为斜边作等腰直角三角形,如图③所示,(1)中的结论仍成立吗(直接写出结论,不需要证明)?
解:(1)由题意得S1=b2,S2=a2,S3=c2.
∵a2+b2=c2,∴S1+S2=S3.
(2):仍成立.理由如下:易得S1=·b2,S2=·a2,S3=·c2,
∵a2+b2=c2,∴S1+S2=S3.
即(1)中的结论仍成立.
:S1+S2=S3仍成立.
18.在Rt△ABC中,AC⊥CB,AC=15,AB=25,点D为斜边AB上的动点.
(1)如图①,过点D作DE⊥AB交CB于点E,连接AE,当AE平分∠CAB时,求CE的长;
(2)如图②,连接CD,若△ACD为等腰三角形,求AD的长.
解:(1)∵AC⊥CB,AC=15,AB=25,∴BC=20.
∵AE平分∠CAB,∴∠EAC=∠EAD.
∵AC⊥CB,DE⊥AB,∴∠ECA=∠EDA=90°.
又∵AE=AE,∴△ACE≌△ADE(AAS),
∴CE=DE,AC=AD=15.∴BD=25-15=10.
设CE=DE=x,则BE=20-x,
在Rt△BED中,x2+102=(20-x)2,∴x=7.5,∴CE=7.5.
(2):①当AD=AC时,△ACD为等腰三角形.
∵AC=15,∴AD=AC=15.
②当CD=AD时,△ACD为等腰三角形.
∵CD=AD,∴∠DCA=∠CAD.
∵AC⊥CB,∴∠CAB+∠B=90°,∠DCA+∠BCD=90°,
∴∠B=∠BCD,∴BD=CD,∴AD=BD=12.5.
③当CD=AC时,△ACD为等腰三角形,
如图,过点C作CH⊥BA于点H,易知AB·CH=AC·BC.
∵AC=15,BC=20,AB=25,∴CH=12.
∴在Rt△ACH中,AH==9.
∵CD=AC,CH⊥BA,∴DH=HA=9,
∴AD=18.
综上,AD的长为15或12.5或18.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
