2020-2021学年 10.5.1机械效率—沪科版八年级物理全册课件(共16张PPT)
文档属性
| 名称 | 2020-2021学年 10.5.1机械效率—沪科版八年级物理全册课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 749.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-02-20 13:18:31 | ||
图片预览




文档简介
第五节
机械效率
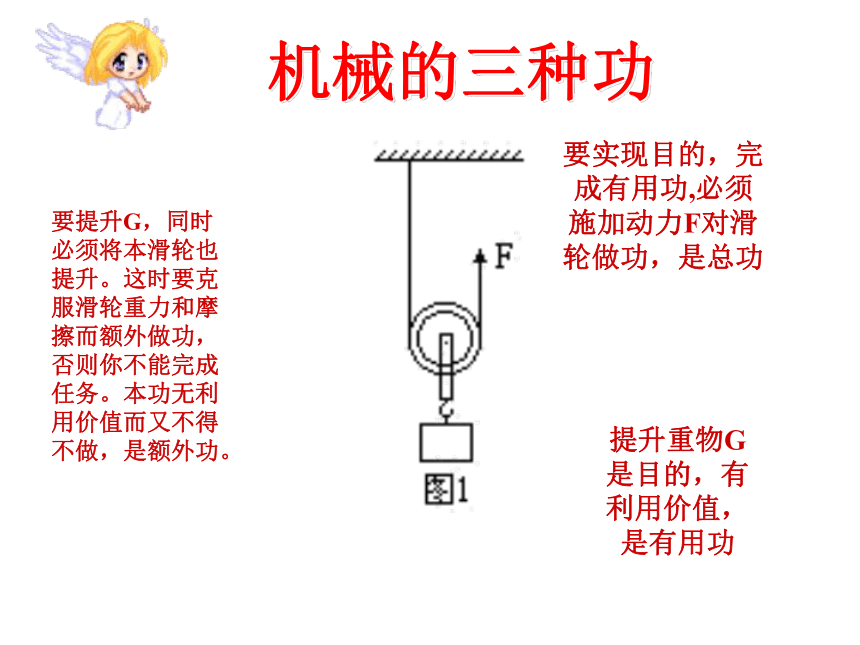
机械的三种功
要提升G,同时必须将本滑轮也提升。这时要克服滑轮重力和摩擦而额外做功,否则你不能完成任务。本功无利用价值而又不得不做,是额外功。
提升重物G是目的,有利用价值,是有用功
要实现目的,完成有用功,必须施加动力F对滑轮做功,是总功
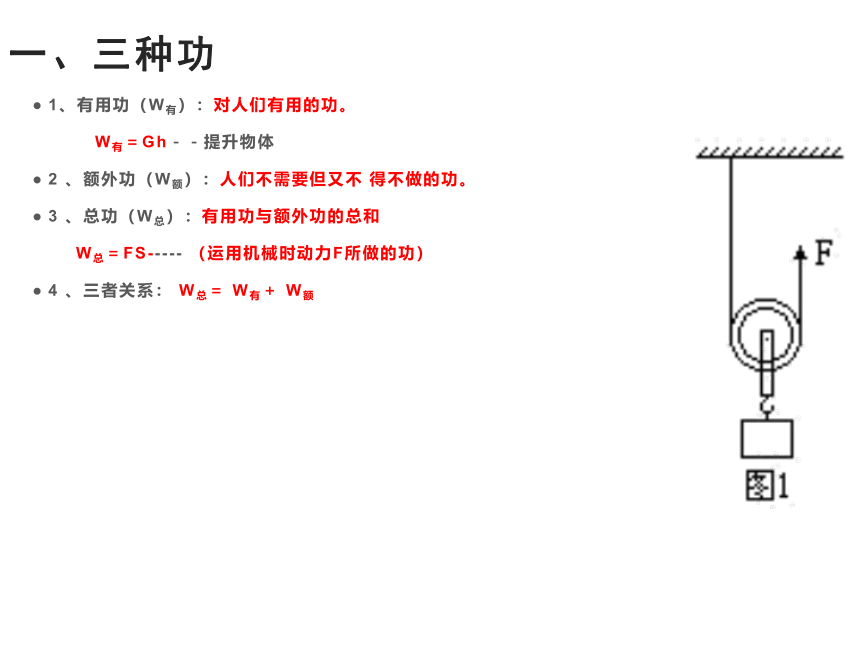
一、三种功
1、有用功(W有):对人们有用的功。
W有=Gh--提升物体
2 、额外功(W额):人们不需要但又不 得不做的功。
3 、总功(W总):有用功与额外功的总和
W总=FS----- (运用机械时动力F所做的功)
4 、三者关系: W总= W有+ W额
机械效率
有用功跟总功的比值叫机械效率
有用功总小于总功,所以机械效率总小于1
看看刚才的数据,思考机械效率会大于1吗?为什么?
公式:
机械效率一般用百分数表示,没有单位
机械效率是
有用功与总功的比值。
反映机械性能的重要指标,总小于1。
不是固定不变的。(同一机械在不同的做功过程中往往会不同)
功的原理:使用任何机械都不能省功
在现实中,使用任何机械都不能省有用功
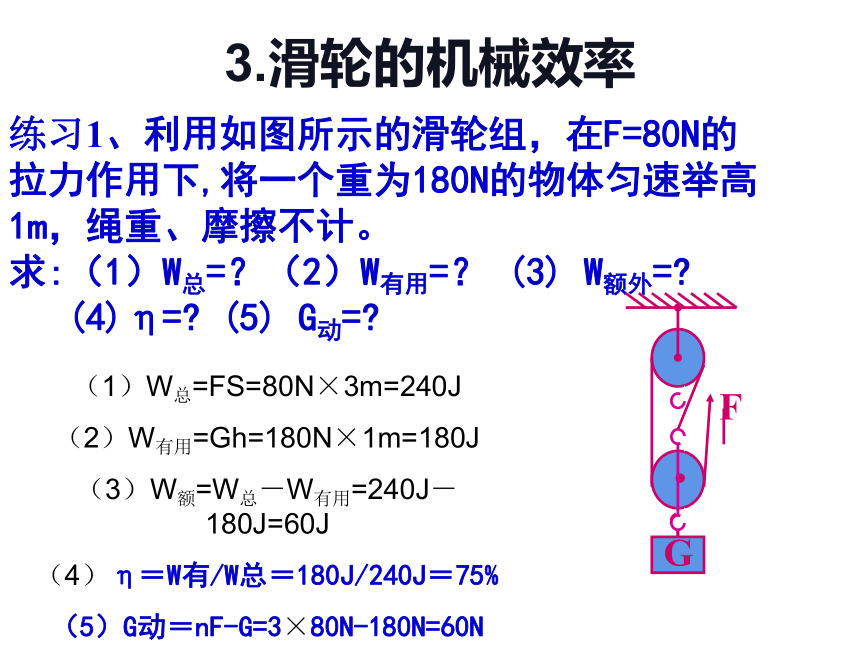
练习1、利用如图所示的滑轮组,在F=80N的拉力作用下,将一个重为180N的物体匀速举高1m,绳重、摩擦不计。
求:(1)W总=?(2)W有用=? (3) W额外=?
(4)η=? (5) G动=?
G
F
.
3.滑轮的机械效率
(1)W总=FS=80N×3m=240J
(2)W有用=Gh=180N×1m=180J
(3)W额=W总-W有用=240J-180J=60J
(4)η=W有/W总=180J/240J=75%
(5)G动=nF-G=3×80N-180N=60N
例2:图示的滑轮组在4s内将重为900N的重物以0.5m/s的速度匀速提升了一段距离,所用的拉力为500N。 (1)拉力做功的功率为多少? (2)这一滑轮组的机械效率为多少?(3)若不计绳重和摩擦,动滑轮重为多少?
解:
(2)W有用=Gh=900N×2m=1800J
(3)W额=W总-W有用=2000J-1800J=200J
由W额=G动h得:
G动=W额/h=200J/2m=100N
(1) h=V物t= 0.5m/s×4s= 2m
S=2h=4m
W总=FS=500N×4m=2000J
P拉=W总/s=2000J/4m=50W
机械效率公式变形
机械效率公式变形
练习2、小明用100N的力沿竖直方向将杠杆的一端拉下2m,杠杆的另一端将320N的重物提高了0.5m,
(1)他做的有用功是多少?
(2)总功是多少?
(3)杠杆的机械效率是多少?
1.杠杆的机械效率
(1)W总=FS=100N×2m=200J
(2)W有用=Gh=320N×0.5m=160J
(3)η=W有/W总=160J/200J=80%
2.斜面的机械效率
如图中斜面高为2m,长为10m,将100N重的物体沿着斜面由底端匀速拉到顶端,需要平行于斜面的力为25N,求拉力所做的功和斜面效率的效率。斜面的摩擦力。
(1)W总=FS=25N×10m=250J
(2)W有用=Gh=100N×2m=200J
(3)η=W有/W总=200J/250J=80%
(4)W外=W总-W有用=250J-200J=50J
(5)f=W外/L=50J/10m=0.5N
使用起重机提升重物时所做的有用功跟总功的比值是60%,也可以说有用功在总功中占有60%,另外的40%是额外功.
起重机的机械效率是60%,它表示什么意思?
一些机械的机械效率:
知识小结
一、机械的三种功:
有用功——有利用价值的功。
总功——动力对机械所做的功。
额外功——对人们无利用价值而又不得不做的功。
二、机械效率:
1、定义:有用功与总功的比值。
2、公式讨论:
请你判断:下面说法中是否正确?
1.有用功越多,机械效率越高( )
2.额外功越少,机械效率越高( )
3.物体做功越慢,机械效率越低( )
4.做总功越多,机械效率越低( )
5.做相同的有用功,额外功越少,机械效率越高( )
6.做相同的总功时,有用功越多,机械效率越高( )
7.机械效率越高,越省力( )
√
√
×
×
×
×
×
1、下列判断正确的是( )
A、机械的功率越大,做的功越多。
B、机械的功率越大,效率越高。
C、机械的功率越大,做功越快。
D、机械所做的用功越多效率越高。
2、一滑轮组经改进后提高了机械效率,用它把同一物体匀速提升同样的高度,改进后比改进前( )
A、有用功减少,总功减少
B、有用功增加,总功增加
C、有用功不变,总功不变
D、有用功不变,总功减少
C
D
功的原理:
使用任何机械都不能省有用功
功率和效率是两个完全不同的概念
机械效率
机械的三种功
要提升G,同时必须将本滑轮也提升。这时要克服滑轮重力和摩擦而额外做功,否则你不能完成任务。本功无利用价值而又不得不做,是额外功。
提升重物G是目的,有利用价值,是有用功
要实现目的,完成有用功,必须施加动力F对滑轮做功,是总功
一、三种功
1、有用功(W有):对人们有用的功。
W有=Gh--提升物体
2 、额外功(W额):人们不需要但又不 得不做的功。
3 、总功(W总):有用功与额外功的总和
W总=FS----- (运用机械时动力F所做的功)
4 、三者关系: W总= W有+ W额
机械效率
有用功跟总功的比值叫机械效率
有用功总小于总功,所以机械效率总小于1
看看刚才的数据,思考机械效率会大于1吗?为什么?
公式:
机械效率一般用百分数表示,没有单位
机械效率是
有用功与总功的比值。
反映机械性能的重要指标,总小于1。
不是固定不变的。(同一机械在不同的做功过程中往往会不同)
功的原理:使用任何机械都不能省功
在现实中,使用任何机械都不能省有用功
练习1、利用如图所示的滑轮组,在F=80N的拉力作用下,将一个重为180N的物体匀速举高1m,绳重、摩擦不计。
求:(1)W总=?(2)W有用=? (3) W额外=?
(4)η=? (5) G动=?
G
F
.
3.滑轮的机械效率
(1)W总=FS=80N×3m=240J
(2)W有用=Gh=180N×1m=180J
(3)W额=W总-W有用=240J-180J=60J
(4)η=W有/W总=180J/240J=75%
(5)G动=nF-G=3×80N-180N=60N
例2:图示的滑轮组在4s内将重为900N的重物以0.5m/s的速度匀速提升了一段距离,所用的拉力为500N。 (1)拉力做功的功率为多少? (2)这一滑轮组的机械效率为多少?(3)若不计绳重和摩擦,动滑轮重为多少?
解:
(2)W有用=Gh=900N×2m=1800J
(3)W额=W总-W有用=2000J-1800J=200J
由W额=G动h得:
G动=W额/h=200J/2m=100N
(1) h=V物t= 0.5m/s×4s= 2m
S=2h=4m
W总=FS=500N×4m=2000J
P拉=W总/s=2000J/4m=50W
机械效率公式变形
机械效率公式变形
练习2、小明用100N的力沿竖直方向将杠杆的一端拉下2m,杠杆的另一端将320N的重物提高了0.5m,
(1)他做的有用功是多少?
(2)总功是多少?
(3)杠杆的机械效率是多少?
1.杠杆的机械效率
(1)W总=FS=100N×2m=200J
(2)W有用=Gh=320N×0.5m=160J
(3)η=W有/W总=160J/200J=80%
2.斜面的机械效率
如图中斜面高为2m,长为10m,将100N重的物体沿着斜面由底端匀速拉到顶端,需要平行于斜面的力为25N,求拉力所做的功和斜面效率的效率。斜面的摩擦力。
(1)W总=FS=25N×10m=250J
(2)W有用=Gh=100N×2m=200J
(3)η=W有/W总=200J/250J=80%
(4)W外=W总-W有用=250J-200J=50J
(5)f=W外/L=50J/10m=0.5N
使用起重机提升重物时所做的有用功跟总功的比值是60%,也可以说有用功在总功中占有60%,另外的40%是额外功.
起重机的机械效率是60%,它表示什么意思?
一些机械的机械效率:
知识小结
一、机械的三种功:
有用功——有利用价值的功。
总功——动力对机械所做的功。
额外功——对人们无利用价值而又不得不做的功。
二、机械效率:
1、定义:有用功与总功的比值。
2、公式讨论:
请你判断:下面说法中是否正确?
1.有用功越多,机械效率越高( )
2.额外功越少,机械效率越高( )
3.物体做功越慢,机械效率越低( )
4.做总功越多,机械效率越低( )
5.做相同的有用功,额外功越少,机械效率越高( )
6.做相同的总功时,有用功越多,机械效率越高( )
7.机械效率越高,越省力( )
√
√
×
×
×
×
×
1、下列判断正确的是( )
A、机械的功率越大,做的功越多。
B、机械的功率越大,效率越高。
C、机械的功率越大,做功越快。
D、机械所做的用功越多效率越高。
2、一滑轮组经改进后提高了机械效率,用它把同一物体匀速提升同样的高度,改进后比改进前( )
A、有用功减少,总功减少
B、有用功增加,总功增加
C、有用功不变,总功不变
D、有用功不变,总功减少
C
D
功的原理:
使用任何机械都不能省有用功
功率和效率是两个完全不同的概念
同课章节目录
- 第一章 打开物理世界的大门
- 第一节 走进神奇
- 第二节 探索之路
- 第三节 站在巨人的肩膀上
- 第二章 运动的世界
- 第一节 动与静
- 第二节 长度与时间的测量
- 第三节 快与慢
- 第四节 科学探究:速度的变化
- 第三章 声的世界
- 第一节 科学探究:声音的产生与传播
- 第二节 声音的特性
- 第三节 超声与次声
- 第四章 多彩的光
- 第一节 光的反射
- 第二节 平面镜成像
- 第三节 光的折射
- 第四节 光的色散
- 第五节 科学探究:凸透镜成像
- 第六节 神奇的眼睛
- 第五章 质量与密度
- 第一节 质量
- 第二节 学习使用天平和量筒
- 第三节 科学探究:物质的密度
- 第四节 密度知识的应用
- 第六章 熟悉而陌生的力
- 第一节 力
- 第二节 怎样描述力
- 第三节 弹力与弹簧测力计
- 第四节 来自地球的力
- 第五节 科学探究:摩擦力
- 第七章 力与运动
- 第一节 科学探究:牛顿第一定律
- 第二节 力的合成
- 第三节 力的平衡
- 第八章 压强
- 第一节 压力的作用效果
- 第二节 科学探究:液体的压强
- 第三节 空气的“力量”
- 第四节 流体压强与流速的关系
- 第九章 浮力
- 第一节 认识浮力
- 第二节 阿基米德原理
- 第三节 物体的浮与沉
- 第十章 机械与人
- 第一节 科学探究:杠杆的平衡条件
- 第二节 滑轮及其应用
- 第三节 做功了吗
- 第四节 做功的快慢
- 第五节 机械效率
- 第六节 合理利用机械能
- 第十一章 小粒子与大宇宙
- 第一节 走进微观
- 第二节 看不见的运动
- 第三节 探索宇宙
