2020-2021学年人教版七年级数学下册教学课件-7.1.2平面直角坐标系(27张)
文档属性
| 名称 | 2020-2021学年人教版七年级数学下册教学课件-7.1.2平面直角坐标系(27张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 623.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 12:18:22 | ||
图片预览





文档简介
7.1.2平面直角坐标系
0
-5
-4
-3
-2
-1
1
2
3
4
5
6
-6
7
数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的坐标.
例如点A在数轴上的坐标为-3,点B在数轴上的坐标为6。反过来,知道数轴上一个点的坐标,这个点在数轴上的位置也就确定了。
A
B
O
如何确定直线上点的位置?
小明
小红
小华
1米
温故知新
D
C
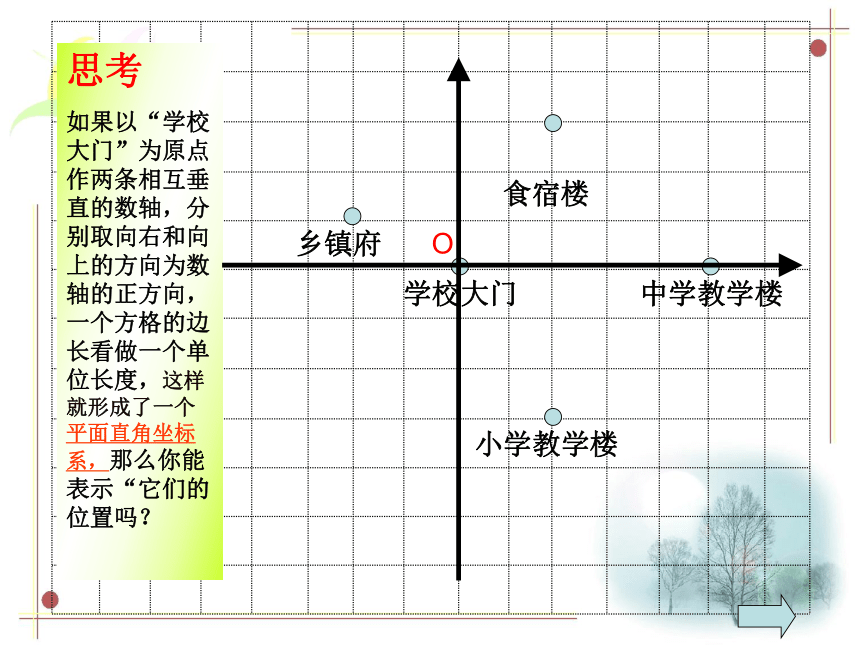
中学教学楼
学校大门
食宿楼
乡镇府
小学教学楼
思考
如图,是我校及周边部分设施的示意图。你如何确定各个点的位置?
中学教学楼
学校大门
食宿楼
乡镇府
小学教学楼
思考
如果以“学校大门”为原点作两条相互垂直的数轴,分别取向右和向上的方向为数轴的正方向,一个方格的边长看做一个单位长度,这样就形成了一个平面直角坐标系,那么你能表示“它们的位置吗?
O
自主学习:
辅导提示:
1、什么叫平面直角坐标系?什么叫横轴、纵轴、原点?
2
、坐标平面被两条互相垂直的数轴分成几部分?每部分分别叫什么?
3、在坐标系中已知一个点如何找出点的坐标?反过来,知道了一个点的坐标在坐标系中描点?
教材第66页最后两自然段到67页前两段
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
原点
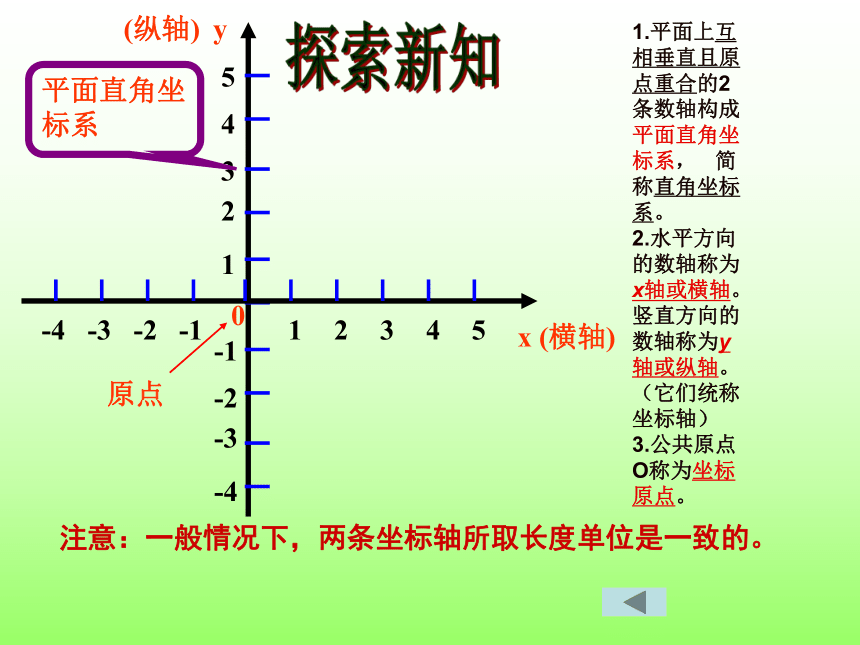
探索新知
平面直角坐标系
注意:一般情况下,两条坐标轴所取长度单位是一致的。
(横轴)
(纵轴)
1.平面上互相垂直且原点重合的2条数轴构成平面直角坐标系,
简称直角坐标系。
2.水平方向的数轴称为x轴或横轴。
竖直方向的数轴称为y轴或纵轴。
(它们统称坐标轴)
3.公共原点O称为坐标原点。
X
O
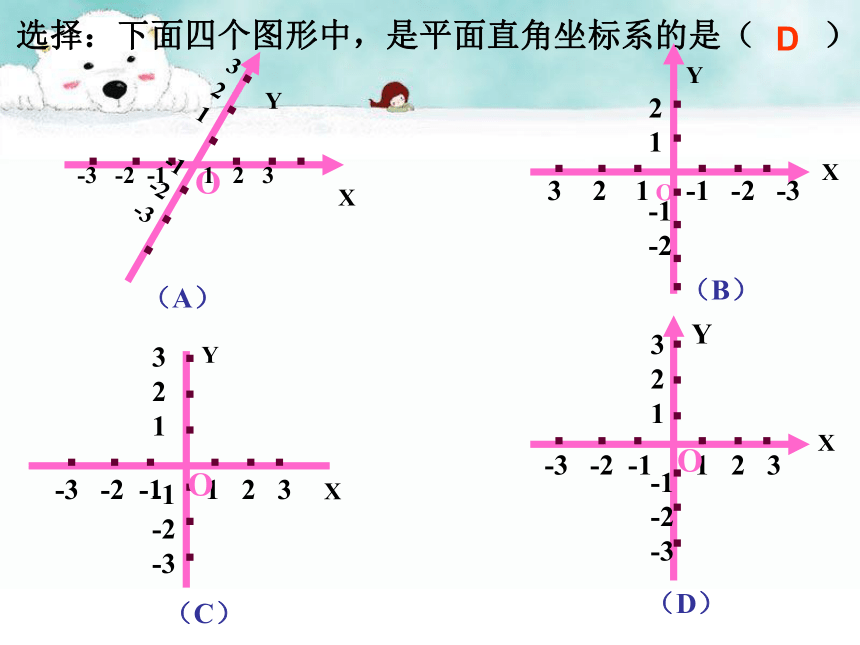
选择:下面四个图形中,是平面直角坐标系的是(
)
-3
-2
-1
1
2
3
3
2
1
-1
-2
-3
Y
X
X
Y
(A)
3
2
1
-1
-2
-3
X
Y
(B)
2
1
-1
-2
O
-3
-2
-1
1
2
3
3
2
1
-1
-2
-3
(C)
O
-3
-2
-1
1
2
3
3
2
1
-1
-2
-3
Y
(D)
O
D
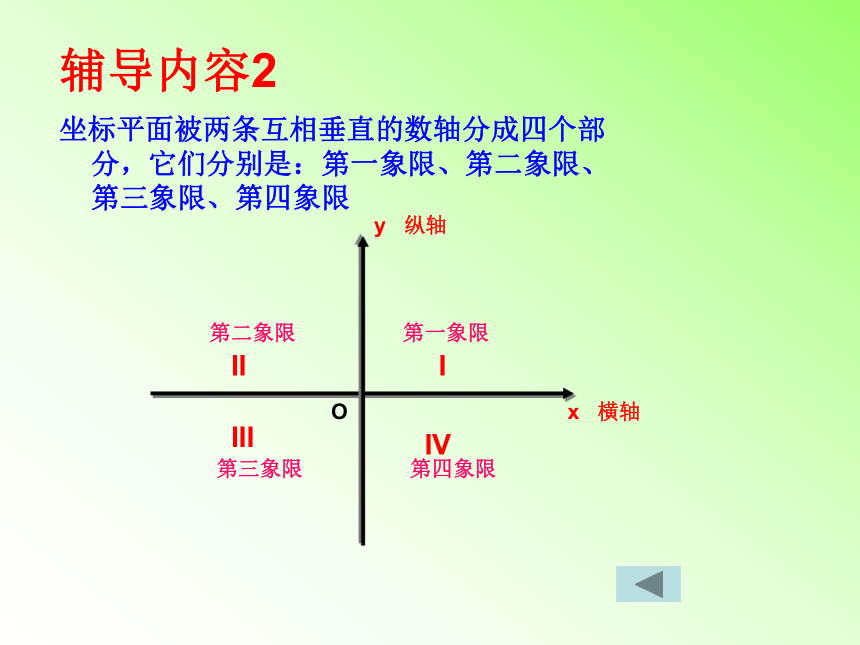
辅导内容2
坐标平面被两条互相垂直的数轴分成四个部分,它们分别是:第一象限、第二象限、第三象限、第四象限
第一象限
第二象限
第四象限
第三象限
y
纵轴
x
横轴
O
I
II
III
IV
你知道吗?
在1637年以前,法国数学家、解析几何的创始人笛卡尔受到了经纬度的启发,最早引入坐标系,用代数方法研究几何图形,所以平面直角坐标系人们也叫它笛卡尔直角坐标系。据说它诞生的灵感源于蜘蛛结网…
活动:
自己建立一个平面直角坐标系
归纳:根据已知条件建立平面直角坐标系的根本思路:
一选
二作
三定
(2,3)
(
-
4
,
1
)
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
(3,2)
·
C
由点A分别向X轴和y轴作垂线
B
3叫做点A的横坐标
2叫做点A的纵坐标
A点在平面内的坐标为(3,
2)
记作:A(3,2)
横坐标写在前,
纵坐标写在后,
中间用逗号隔开
坐标
辅导内容3:在坐标系中如何找出A点的坐标?
记忆顺口溜
平面直角坐标系,两条数轴来唱戏。
一个点,两个数,先横后纵再括号,中间隔开用逗号。
点A到x轴的距离就是点A的纵坐标的绝对值;
点A到y轴的距离就是点A的横坐标的绝对值
5
-5
-2
-3
-4
-1
3
2
4
1
-6
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
x
·
·
A
(
4,5
)
2
辅导内容3
在平面直角坐标系中
如何由坐标描点?
(
4,5
)
A
归纳:由坐标描点的基本步骤:
1.先在横轴上找出表示横坐标的点,过这个点做横轴的垂线
2.再在纵轴上找出表示纵坐标的点,过这个点做纵轴的垂线
两条垂线的交点就是所要描出的点
做一做:认识了坐标平面之后,请同学们在所给的平面直角坐标系中描出下列各点
A(3,2)
B(-3,-2)
C(3,-2)
D(-3,2)
E(2,3)
F(-2,-3)
G(2,-3)
H(-2,3)
I(0,4)
J(4,0)
K(-4,0)
L(0,-4)
0
1
2
3
4
5
-4
-3
-2
-1
·
·
A(3,2)
B(-3,-2)
·
C(3,-2)
·
D(-3,2)
·
E(2,3)
·
F(-2,-3)
·
G(2,-3)
·
H(-2,3)
·
I(0,4)
·
J(4,0)
·
K(-4,0)
·
L(0,-4)
x
y
第一象限
第二象限
第三象限
第四象限
3
1
4
2
5
-2
-4
-1
-3
问题:各个象限内点的坐标符号有什么特征?
坐标轴上的点的坐标符号有什么特征?
第一象限:(+,+)
第二象限:(-,+)
第三象限:(-,-)
第四象限:(+,-)
x轴正半轴:(+,0)
x轴负半轴:(-,0)
y轴正半轴:(0,+)
y轴负半轴:(0,-)
原点:
(0,0)
归纳:
实战演练:
A(-2,3);B(1,-2);C(-1,-2);
D(3,2);E(-3,0);
F(0,1);
2)
已知点P(0,a)在y轴的负半轴,则Q(a,-2)在(
)
(A)第一象限
(B)第二象限
(C)第三象限
(D)第四象限
1)指出下列各点所在的象限或坐标轴
问题探究:(1)请同学们将刚才所画的直角坐标系沿x轴对折,你发现有那些点会重合?这说明了什么?此时,这些点的横、纵坐标有什么相同点和不同点?如果沿y轴对折呢?
(2)请同学们观察点A与点B、点C与点D的坐标,有何关系?点A与点D
、
D
、点B与C呢?点A与点C
、点B与点D呢?
0
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
·
·
·
A
C
D
.
B
x
y
归纳:
(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数。顺口记忆--纵变横不变
(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数。顺口记忆--横变纵不变
(3)关于原点对称的点,横纵坐标都互为相反数。顺口记忆--横纵都要变
反之亦然
练一练
填空:
(1)已知点P(3,1),则它关于x轴的对称点坐标
.
(2)已知点P(3,1),则它关于y轴的对称点坐标
.
(3)已知点P(3,1),则它关于原点的对称点坐标
.
(4)已知点P(x,y)与Q(2,6)关于原点对称,则x=
,y=
.
0
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
·
A(3,2)
·
C(3,-2)
·
D(-3,2)
问题探究:
(1)连接AC、BD,则线段AC、BD分别与坐标轴有怎样的位置关系
(2)连接AD、BC,则线段AD、BC分别与坐标轴有怎样的位置关系
.
B(–3,–2)
平行于x轴的直线上的所有点的纵坐标都相同
平行于y轴的直线上的所有点的横坐标都相同
拓展练习
一、填空题.
1.如果点P(a+5,a?2)在x轴上,那么P点坐标为________.
2.点M(a,b)在第二象限,则点N(?b,b?a)在________象限.
3.点A(3,a)在x轴上,点B(b,4)在y轴上,则a=______,b=______,S△AOB=_____.
二、选择题:
1.已知的平面直角坐标系中A(?3,0)在(
)
A.x轴正半轴上
B.x轴负半轴上;
C.y轴正半轴上
D.y轴负半轴上
2.点M(a,b)的坐标ab=0,那么M(a,b)位置在(
)
A.y轴上
B.x轴上;
C.x轴或y轴上
D.原点
这节课你有什么收获?
小结
请说给老师和同学听听
小结:
这节课主要学面直角坐标系的有关概念
1、
会建立直角坐标系,并根据坐标找点,会由坐标系内的点写坐标
2、坐标平面内的点与有序数对是一一对应的。
3、了解坐标轴上(原点、x轴,y轴)以及各象限内点的坐标的特点
作业布置:
P70页
第5
题
,
第7题
1
2
3
-3
x
-2
·
-2
-3
o
-1
y
4
2
5
3
6
1
在如图建立的直角坐标系中描出下列各组点,并将各组的点用线段依次连接起来.
做
一
做
①(0
,
6),
(-4,
3),
(4
,
3)
②(-2
,
3),
(-2
,
-3),
(2
,
-3),
(2
,
3)
·
·
·
·
·
·
观察所得的图形,你觉得它象什么?
-4
-1
4
A(-4,3)
B(4,3)
C(-2,3)
D(2,3)
E(-2,-3)
F(2,-3)
(0
,
6)
·
再见
·
P(x,y)
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
-5
预习作业:P点到x轴、y轴的距离与P点的坐标有何关系?
P点到x轴的距离就是点的纵坐标的绝对值;
P点到y轴的距离就是点的横坐标的绝对值;
x
y
实战演练
选择题
(1)点
位于
轴左方,距
轴3个单位长,则点
的坐标可能是( ).
A、(3,-4)
B、(-3,4)
C、(4,-3)
D、(-4,3)
(2)直角坐标系中,点P(x,y)在第二象限,且P
到
x
轴、y轴距离分别为3,7,则点P坐标为(
).
A、(-3,-7)
B、(-7,3)
C、(-3,7)
D、(7,3)
B
B
B
0
-5
-4
-3
-2
-1
1
2
3
4
5
6
-6
7
数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的坐标.
例如点A在数轴上的坐标为-3,点B在数轴上的坐标为6。反过来,知道数轴上一个点的坐标,这个点在数轴上的位置也就确定了。
A
B
O
如何确定直线上点的位置?
小明
小红
小华
1米
温故知新
D
C
中学教学楼
学校大门
食宿楼
乡镇府
小学教学楼
思考
如图,是我校及周边部分设施的示意图。你如何确定各个点的位置?
中学教学楼
学校大门
食宿楼
乡镇府
小学教学楼
思考
如果以“学校大门”为原点作两条相互垂直的数轴,分别取向右和向上的方向为数轴的正方向,一个方格的边长看做一个单位长度,这样就形成了一个平面直角坐标系,那么你能表示“它们的位置吗?
O
自主学习:
辅导提示:
1、什么叫平面直角坐标系?什么叫横轴、纵轴、原点?
2
、坐标平面被两条互相垂直的数轴分成几部分?每部分分别叫什么?
3、在坐标系中已知一个点如何找出点的坐标?反过来,知道了一个点的坐标在坐标系中描点?
教材第66页最后两自然段到67页前两段
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
原点
探索新知
平面直角坐标系
注意:一般情况下,两条坐标轴所取长度单位是一致的。
(横轴)
(纵轴)
1.平面上互相垂直且原点重合的2条数轴构成平面直角坐标系,
简称直角坐标系。
2.水平方向的数轴称为x轴或横轴。
竖直方向的数轴称为y轴或纵轴。
(它们统称坐标轴)
3.公共原点O称为坐标原点。
X
O
选择:下面四个图形中,是平面直角坐标系的是(
)
-3
-2
-1
1
2
3
3
2
1
-1
-2
-3
Y
X
X
Y
(A)
3
2
1
-1
-2
-3
X
Y
(B)
2
1
-1
-2
O
-3
-2
-1
1
2
3
3
2
1
-1
-2
-3
(C)
O
-3
-2
-1
1
2
3
3
2
1
-1
-2
-3
Y
(D)
O
D
辅导内容2
坐标平面被两条互相垂直的数轴分成四个部分,它们分别是:第一象限、第二象限、第三象限、第四象限
第一象限
第二象限
第四象限
第三象限
y
纵轴
x
横轴
O
I
II
III
IV
你知道吗?
在1637年以前,法国数学家、解析几何的创始人笛卡尔受到了经纬度的启发,最早引入坐标系,用代数方法研究几何图形,所以平面直角坐标系人们也叫它笛卡尔直角坐标系。据说它诞生的灵感源于蜘蛛结网…
活动:
自己建立一个平面直角坐标系
归纳:根据已知条件建立平面直角坐标系的根本思路:
一选
二作
三定
(2,3)
(
-
4
,
1
)
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
(3,2)
·
C
由点A分别向X轴和y轴作垂线
B
3叫做点A的横坐标
2叫做点A的纵坐标
A点在平面内的坐标为(3,
2)
记作:A(3,2)
横坐标写在前,
纵坐标写在后,
中间用逗号隔开
坐标
辅导内容3:在坐标系中如何找出A点的坐标?
记忆顺口溜
平面直角坐标系,两条数轴来唱戏。
一个点,两个数,先横后纵再括号,中间隔开用逗号。
点A到x轴的距离就是点A的纵坐标的绝对值;
点A到y轴的距离就是点A的横坐标的绝对值
5
-5
-2
-3
-4
-1
3
2
4
1
-6
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
x
·
·
A
(
4,5
)
2
辅导内容3
在平面直角坐标系中
如何由坐标描点?
(
4,5
)
A
归纳:由坐标描点的基本步骤:
1.先在横轴上找出表示横坐标的点,过这个点做横轴的垂线
2.再在纵轴上找出表示纵坐标的点,过这个点做纵轴的垂线
两条垂线的交点就是所要描出的点
做一做:认识了坐标平面之后,请同学们在所给的平面直角坐标系中描出下列各点
A(3,2)
B(-3,-2)
C(3,-2)
D(-3,2)
E(2,3)
F(-2,-3)
G(2,-3)
H(-2,3)
I(0,4)
J(4,0)
K(-4,0)
L(0,-4)
0
1
2
3
4
5
-4
-3
-2
-1
·
·
A(3,2)
B(-3,-2)
·
C(3,-2)
·
D(-3,2)
·
E(2,3)
·
F(-2,-3)
·
G(2,-3)
·
H(-2,3)
·
I(0,4)
·
J(4,0)
·
K(-4,0)
·
L(0,-4)
x
y
第一象限
第二象限
第三象限
第四象限
3
1
4
2
5
-2
-4
-1
-3
问题:各个象限内点的坐标符号有什么特征?
坐标轴上的点的坐标符号有什么特征?
第一象限:(+,+)
第二象限:(-,+)
第三象限:(-,-)
第四象限:(+,-)
x轴正半轴:(+,0)
x轴负半轴:(-,0)
y轴正半轴:(0,+)
y轴负半轴:(0,-)
原点:
(0,0)
归纳:
实战演练:
A(-2,3);B(1,-2);C(-1,-2);
D(3,2);E(-3,0);
F(0,1);
2)
已知点P(0,a)在y轴的负半轴,则Q(a,-2)在(
)
(A)第一象限
(B)第二象限
(C)第三象限
(D)第四象限
1)指出下列各点所在的象限或坐标轴
问题探究:(1)请同学们将刚才所画的直角坐标系沿x轴对折,你发现有那些点会重合?这说明了什么?此时,这些点的横、纵坐标有什么相同点和不同点?如果沿y轴对折呢?
(2)请同学们观察点A与点B、点C与点D的坐标,有何关系?点A与点D
、
D
、点B与C呢?点A与点C
、点B与点D呢?
0
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
·
·
·
A
C
D
.
B
x
y
归纳:
(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数。顺口记忆--纵变横不变
(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数。顺口记忆--横变纵不变
(3)关于原点对称的点,横纵坐标都互为相反数。顺口记忆--横纵都要变
反之亦然
练一练
填空:
(1)已知点P(3,1),则它关于x轴的对称点坐标
.
(2)已知点P(3,1),则它关于y轴的对称点坐标
.
(3)已知点P(3,1),则它关于原点的对称点坐标
.
(4)已知点P(x,y)与Q(2,6)关于原点对称,则x=
,y=
.
0
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
·
A(3,2)
·
C(3,-2)
·
D(-3,2)
问题探究:
(1)连接AC、BD,则线段AC、BD分别与坐标轴有怎样的位置关系
(2)连接AD、BC,则线段AD、BC分别与坐标轴有怎样的位置关系
.
B(–3,–2)
平行于x轴的直线上的所有点的纵坐标都相同
平行于y轴的直线上的所有点的横坐标都相同
拓展练习
一、填空题.
1.如果点P(a+5,a?2)在x轴上,那么P点坐标为________.
2.点M(a,b)在第二象限,则点N(?b,b?a)在________象限.
3.点A(3,a)在x轴上,点B(b,4)在y轴上,则a=______,b=______,S△AOB=_____.
二、选择题:
1.已知的平面直角坐标系中A(?3,0)在(
)
A.x轴正半轴上
B.x轴负半轴上;
C.y轴正半轴上
D.y轴负半轴上
2.点M(a,b)的坐标ab=0,那么M(a,b)位置在(
)
A.y轴上
B.x轴上;
C.x轴或y轴上
D.原点
这节课你有什么收获?
小结
请说给老师和同学听听
小结:
这节课主要学面直角坐标系的有关概念
1、
会建立直角坐标系,并根据坐标找点,会由坐标系内的点写坐标
2、坐标平面内的点与有序数对是一一对应的。
3、了解坐标轴上(原点、x轴,y轴)以及各象限内点的坐标的特点
作业布置:
P70页
第5
题
,
第7题
1
2
3
-3
x
-2
·
-2
-3
o
-1
y
4
2
5
3
6
1
在如图建立的直角坐标系中描出下列各组点,并将各组的点用线段依次连接起来.
做
一
做
①(0
,
6),
(-4,
3),
(4
,
3)
②(-2
,
3),
(-2
,
-3),
(2
,
-3),
(2
,
3)
·
·
·
·
·
·
观察所得的图形,你觉得它象什么?
-4
-1
4
A(-4,3)
B(4,3)
C(-2,3)
D(2,3)
E(-2,-3)
F(2,-3)
(0
,
6)
·
再见
·
P(x,y)
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
-5
预习作业:P点到x轴、y轴的距离与P点的坐标有何关系?
P点到x轴的距离就是点的纵坐标的绝对值;
P点到y轴的距离就是点的横坐标的绝对值;
x
y
实战演练
选择题
(1)点
位于
轴左方,距
轴3个单位长,则点
的坐标可能是( ).
A、(3,-4)
B、(-3,4)
C、(4,-3)
D、(-4,3)
(2)直角坐标系中,点P(x,y)在第二象限,且P
到
x
轴、y轴距离分别为3,7,则点P坐标为(
).
A、(-3,-7)
B、(-7,3)
C、(-3,7)
D、(7,3)
B
B
B
