2020-2021学年人教版七年级数学下册 课件 5.1.2垂线(17张)
文档属性
| 名称 | 2020-2021学年人教版七年级数学下册 课件 5.1.2垂线(17张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 00:00:00 | ||
图片预览



文档简介
垂线
人教版数学教材七年级下5.1相交线
难点名称 :用垂线定义判断两条直线是否垂直及垂线的画法。
目录
CONTENTS
2
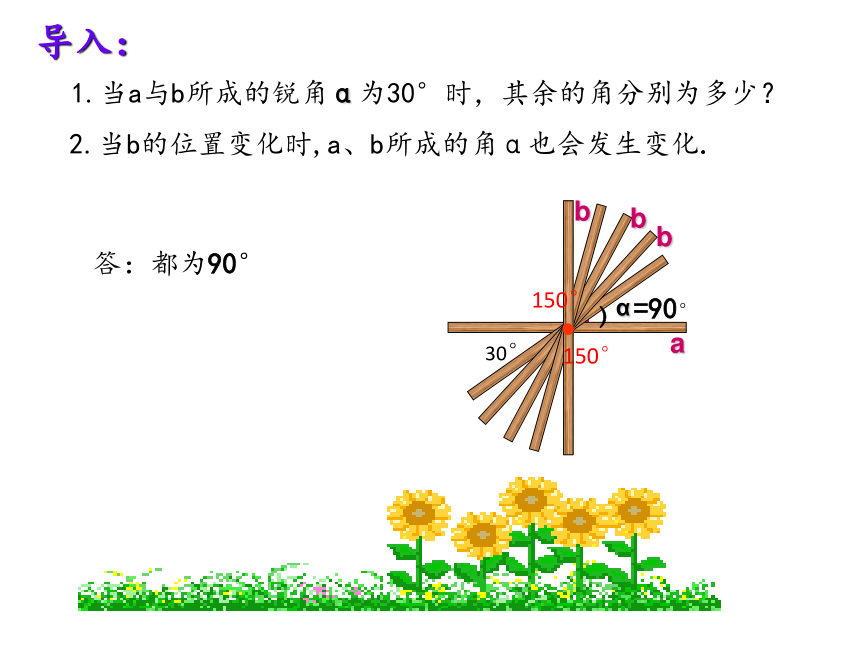
2.当b的位置变化时,a、b所成的角α也会发生变化.
)
α
a
b
b
b
1.当a与b所成的锐角α为30°时,其余的角分别为多少?
30°
150°
150°
导入:
=90°
答:都为90°
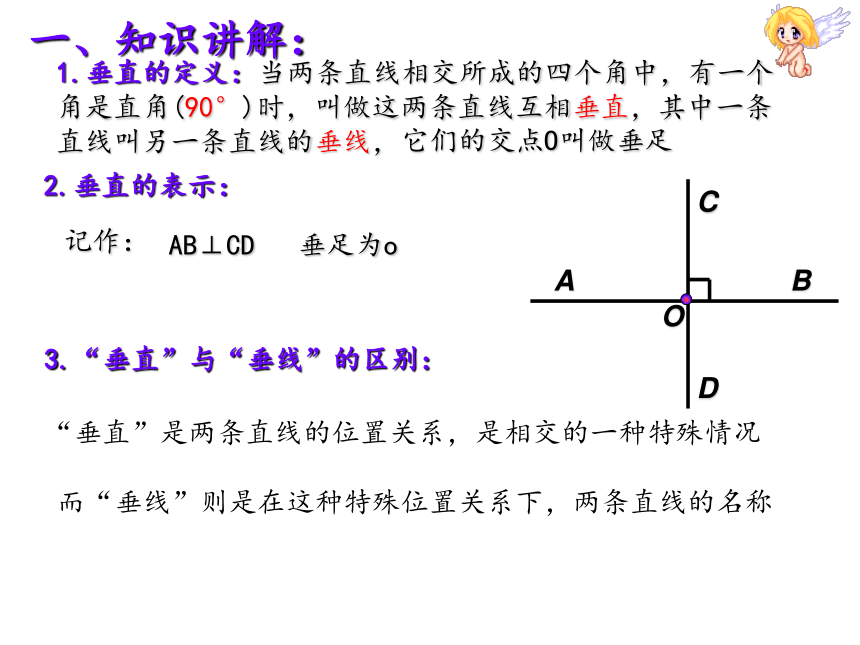
O
D
C
B
A
记作:
AB⊥CD 垂足为o
它们的交点O叫做垂足
一、知识讲解:
1.垂直的定义:当两条直线相交所成的四个角中,有一个角是直角(90°)时,叫做这两条直线互相垂直,其中一条直线叫另一条直线的垂线,
2.垂直的表示:
3.“垂直”与“垂线”的区别:
“垂直”是两条直线的位置关系,是相交的一种特殊情况
而“垂线”则是在这种特殊位置关系下,两条直线的名称
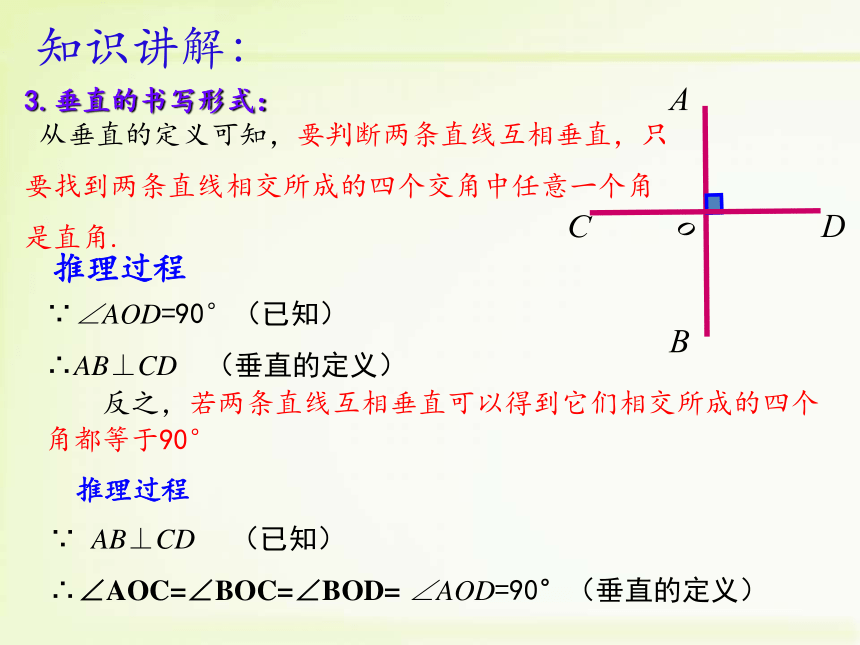
从垂直的定义可知,要判断两条直线互相垂直,只
要找到两条直线相交所成的四个交角中任意一个角
是直角.
A
B
C
D
o
3.垂直的书写形式:
推理过程
∵∠AOD=90°(已知)
∴AB⊥CD (垂直的定义)
反之,若两条直线互相垂直可以得到它们相交所成的四个角都等于90°
∵ AB⊥CD (已知)
∴∠AOC=∠BOC=∠BOD= ∠AOD=90°(垂直的定义)
推理过程
知识讲解:
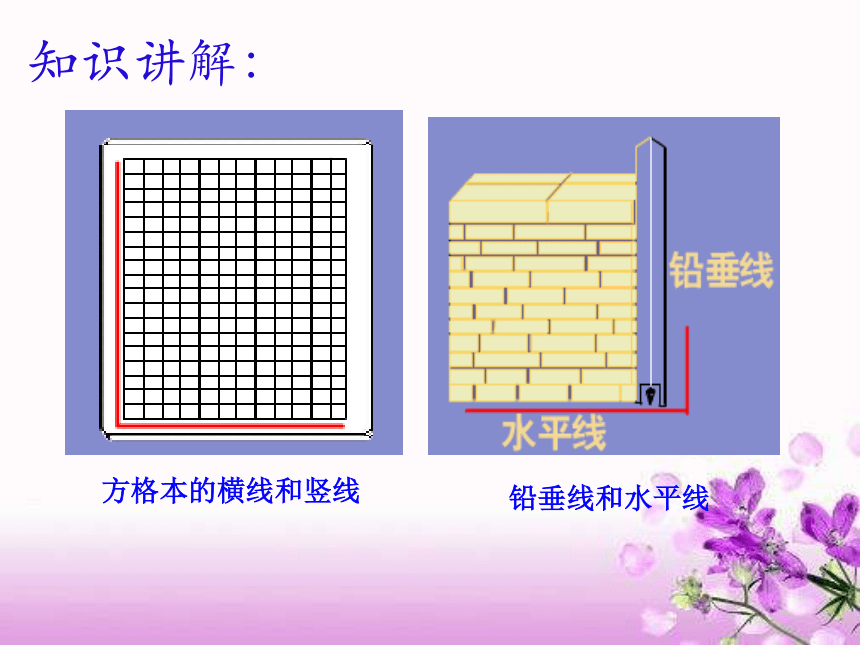
日常生活中,两条直线互相垂直的情形很常见,如下图
你能再举出其他例子吗?
知识讲解:
方格本的横线和竖线
铅垂线和水平线
知识讲解:
如图,已知DO⊥CO,∠1=36°,∠3=36°.
(1)求∠2的度数;
(2)AO与BO垂直吗?说明理由.
解:(1)∵ DO⊥CO
∴∠DOC=90(垂直的定义)
∵ ∠1=36°
∴∠2=90°-36°=54°
(2)AO⊥BO.理由如下:
∵ ∠3=36°,∠2=54°
∴∠3+∠2=90°
∴AO⊥BO(垂直的定义)
课堂练习:
难点巩固:
l
O
用三角尺或量角器画已知直线 的垂线.
这样的直线能画出几条?
A
二、垂线的性质:
探究1:
请同学们画一下
无数条
知识讲解:
二、垂线的性质
探究2:
经过一点画已知直线的垂线,
这样的垂线能画出几条?
①经过一点画已知直线的垂线有几种情况 ?
两种情况:
A B
P
(1)已知点在直线AB外
A
B
P
(2)已知点在直线AB上
思考
②通过画图,你发现过一点可以画几条直
线与已知直线垂直呢?
知识讲解:
l
A
已知直线 和 外的一点A ,作 的垂线.
B
则所画直线AB是过点A的直线l的垂线.
请同学们画一下
二、垂线的性质
如图:
l
l
l
知识讲解:
l
A
已知直线 和 上的一点A ,作 的垂线.
B
则所画直线AB是过点A的直线l的垂线.
如图:
二、垂线的性质
l
l
l
知识讲解:
m
m
A
A
二、垂线的性质
垂线的性质1:在同一平面内,过一点有且只有一条直线与已知直线垂直.
知识讲解:
(1)
你能折出互相垂直的线吗?您不妨试试看!
(3)
(2)
(4)
用折纸法折出垂线
课堂练习:
A
B
P
P
A
B
1. 过点P作线段AB或射线AB的垂线,就是画它们所在直线的垂线
课堂练习:
小结:
垂线的性质
垂线的定义
垂直
人教版数学教材七年级下5.1相交线
难点名称 :用垂线定义判断两条直线是否垂直及垂线的画法。
目录
CONTENTS
2
2.当b的位置变化时,a、b所成的角α也会发生变化.
)
α
a
b
b
b
1.当a与b所成的锐角α为30°时,其余的角分别为多少?
30°
150°
150°
导入:
=90°
答:都为90°
O
D
C
B
A
记作:
AB⊥CD 垂足为o
它们的交点O叫做垂足
一、知识讲解:
1.垂直的定义:当两条直线相交所成的四个角中,有一个角是直角(90°)时,叫做这两条直线互相垂直,其中一条直线叫另一条直线的垂线,
2.垂直的表示:
3.“垂直”与“垂线”的区别:
“垂直”是两条直线的位置关系,是相交的一种特殊情况
而“垂线”则是在这种特殊位置关系下,两条直线的名称
从垂直的定义可知,要判断两条直线互相垂直,只
要找到两条直线相交所成的四个交角中任意一个角
是直角.
A
B
C
D
o
3.垂直的书写形式:
推理过程
∵∠AOD=90°(已知)
∴AB⊥CD (垂直的定义)
反之,若两条直线互相垂直可以得到它们相交所成的四个角都等于90°
∵ AB⊥CD (已知)
∴∠AOC=∠BOC=∠BOD= ∠AOD=90°(垂直的定义)
推理过程
知识讲解:
日常生活中,两条直线互相垂直的情形很常见,如下图
你能再举出其他例子吗?
知识讲解:
方格本的横线和竖线
铅垂线和水平线
知识讲解:
如图,已知DO⊥CO,∠1=36°,∠3=36°.
(1)求∠2的度数;
(2)AO与BO垂直吗?说明理由.
解:(1)∵ DO⊥CO
∴∠DOC=90(垂直的定义)
∵ ∠1=36°
∴∠2=90°-36°=54°
(2)AO⊥BO.理由如下:
∵ ∠3=36°,∠2=54°
∴∠3+∠2=90°
∴AO⊥BO(垂直的定义)
课堂练习:
难点巩固:
l
O
用三角尺或量角器画已知直线 的垂线.
这样的直线能画出几条?
A
二、垂线的性质:
探究1:
请同学们画一下
无数条
知识讲解:
二、垂线的性质
探究2:
经过一点画已知直线的垂线,
这样的垂线能画出几条?
①经过一点画已知直线的垂线有几种情况 ?
两种情况:
A B
P
(1)已知点在直线AB外
A
B
P
(2)已知点在直线AB上
思考
②通过画图,你发现过一点可以画几条直
线与已知直线垂直呢?
知识讲解:
l
A
已知直线 和 外的一点A ,作 的垂线.
B
则所画直线AB是过点A的直线l的垂线.
请同学们画一下
二、垂线的性质
如图:
l
l
l
知识讲解:
l
A
已知直线 和 上的一点A ,作 的垂线.
B
则所画直线AB是过点A的直线l的垂线.
如图:
二、垂线的性质
l
l
l
知识讲解:
m
m
A
A
二、垂线的性质
垂线的性质1:在同一平面内,过一点有且只有一条直线与已知直线垂直.
知识讲解:
(1)
你能折出互相垂直的线吗?您不妨试试看!
(3)
(2)
(4)
用折纸法折出垂线
课堂练习:
A
B
P
P
A
B
1. 过点P作线段AB或射线AB的垂线,就是画它们所在直线的垂线
课堂练习:
小结:
垂线的性质
垂线的定义
垂直
