2020-2021学年华东师大版八年级数学下册教学课件 19.1.2 矩形的判定(共21张)
文档属性
| 名称 | 2020-2021学年华东师大版八年级数学下册教学课件 19.1.2 矩形的判定(共21张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 231.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 00:00:00 | ||
图片预览




文档简介
矩形的判定
温故知新
定义:有一个角是直角的平行四边形叫做矩形
矩形性质
角
边
对角线
对称性
四个角都是直角
对边平行且相等
互相平分且相等
中心对称图形,轴对称图形
你知道如何判定一个平行四边形是矩形吗?
矩形的定义:
有一个角是直角的平行四边形是矩形。
你还有其它的判定方法吗?
ABCD
∠A=900
四边形ABCD是矩形
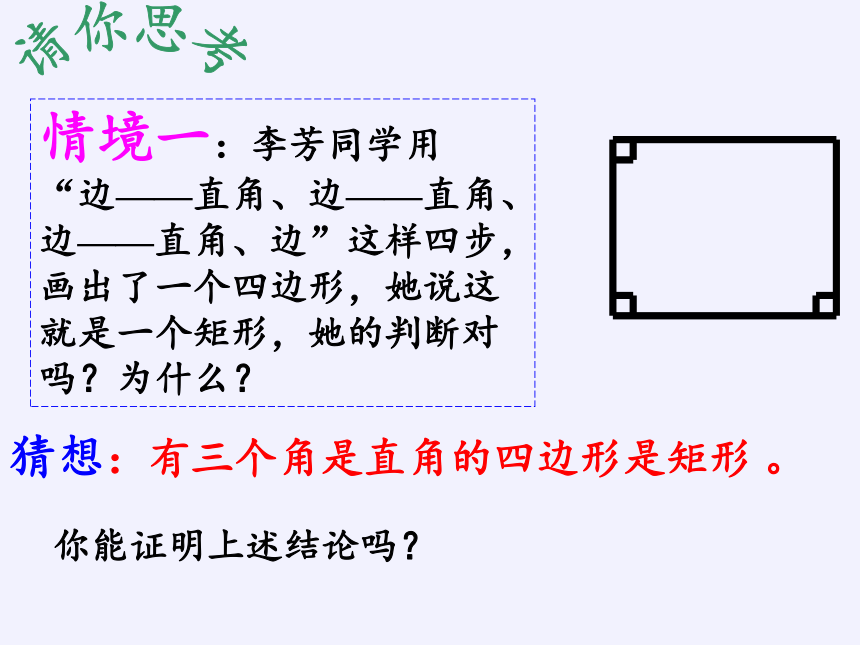
情境一:李芳同学用“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,她说这就是一个矩形,她的判断对吗?为什么?
猜想:有三个角是直角的四边形是矩形 。
你能证明上述结论吗?
请你思考
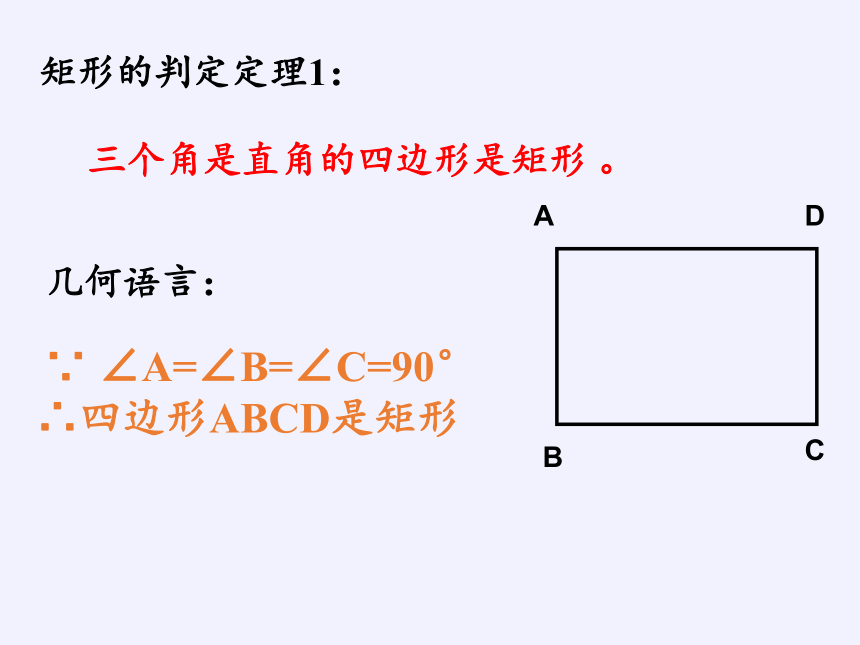
矩形的判定定理1:
三个角是直角的四边形是矩形 。
A
B
C
D
∵ ∠A=∠B=∠C=90°
∴四边形ABCD是矩形
几何语言:
思考:师傅是怎样知道窗户是矩形的呢?
情境二:工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?
猜想:对角线相等的平行四边形是矩形 。
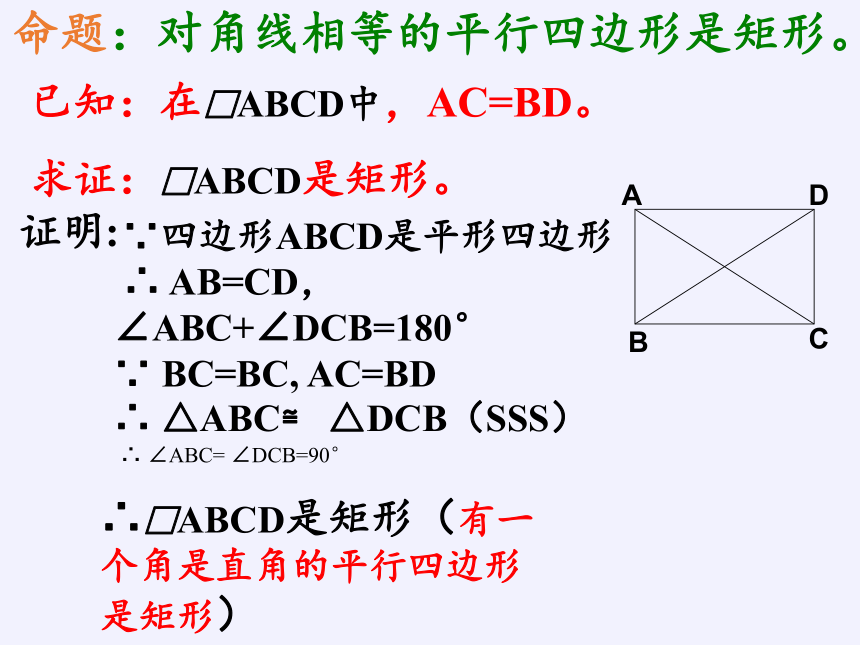
命题:对角线相等的平行四边形是矩形。
已知:在□ABCD中,AC=BD。
求证:□ABCD是矩形。
A
B
C
D
证明:
∵四边形ABCD是平形四边形
∴ AB=CD,∠ABC+∠DCB=180°
∵ BC=BC, AC=BD
∴ △ABC≌ △DCB(SSS)
∴□ABCD是矩形(有一个角是直角的平行四边形是矩形)
∴ ∠ABC= ∠DCB=90°
对角线相等的平行四边形是矩形 。
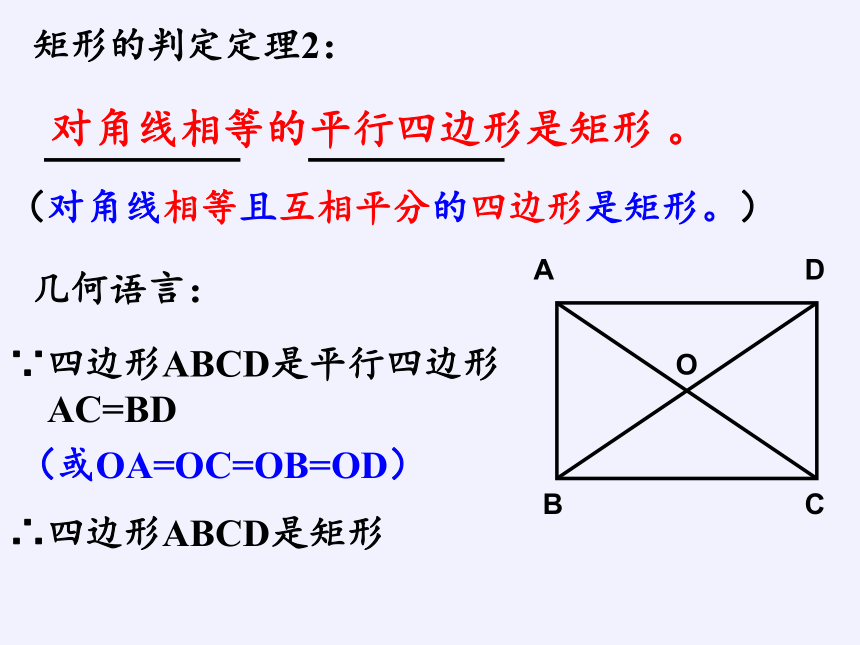
矩形的判定定理2:
几何语言:
∵四边形ABCD是平行四边形
AC=BD
∴四边形ABCD是矩形
(对角线相等且互相平分的四边形是矩形。)
A
B
C
D
O
(或OA=OC=OB=OD)
四边形
平行四边形
矩形
有一个角是直角
有三个角是直角
矩形的判定方法:
1.有一个角是直角的平行四边形叫做矩形(定义)
2.三个角是直角的四边形是矩形(判定定理1)
3.对角线相等的平行四边形是矩形(判定定理2)
对角线相等
例1:如图,M为平行四边形ABCD的边AD的中点,且MB=MC,
求证:平行四边形ABCD是矩形。
A
B
C
D
M
证明:∵四边形ABCD是平形四边形
∴ AB=CD, ∠A+∠D=180°
∵ M为AD的中点
∴AM=DM
又 ∵ MB=MC
∴ △ABM≌ △DCM(SSS)
∴ ∠A= ∠D= 90°
∴四边形ABCD是矩形(有一个角是直角的平行四边形是矩形)
例3:已知,如图.矩形ABCD的对角线AC、BD相交于点O,且E、F、G、H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH.
求证:四边形EFGH是矩形.
证明:∵四边形ABCD是矩形
∴AO=BO=CO=DO
∵AE=BF=CG=DH
∴OE=OF=OG=OH
∴四边形EFGH是平行四边形
∵EO+OG=FO+OH 即EG=FH
∴四边形EFGH是矩形(对角线相等的平行四边形是矩形 )
∠A= ∠B= ∠C=90°
ABCD
AC = BD
ABCD
∠A=90°
ABCD
是矩形
四边形ABCD
是矩形
课堂小结
ABCD
是矩形
作业布置(教材106页习题19.1第2、3题)
下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
(5)有三个角是直角的四边形是矩形;
(6)四个角都相等的四边形是矩形;
(7)对角线相等,且有一个角是直角的四边形是矩形;
(10)一组邻边垂直,一组对边平行且相等的四边形是矩形;
(9)对角线相等且互相垂直的四边形是矩形;
(8)一组对角互补的平行四边形是矩形;
(4)有三个角都相等的四边形是矩形;
X
X
X
X
1.对角线相等且一组对边也相等的四边 形是矩形.
2.两条对角线交点到四个顶点距离相等的四边形为矩形.
3.有一组对边相等,一组对角是直角的四边形是矩形.
4.有三个角都相等的四边形是矩形.
判断题
×
√
√
×
巩固新知
5. 具备条件____的四边形是矩形.
A.两条对角线相等 B.对角线互相垂直
C.一组对角是直角 D.有三个角是直角
6. 能够判断一个四边形是矩形的条件是
A.对角线相等 B.对角线垂直
C.对角线互相平分且相等 D.对角线垂直且相等
选择题
C
D
巩固新知
例1 已知□ABCD的对角线AC、BD交于O,△AOB是等边三角形,AB = 4cm,求这个平行四边形的面积.
A
B
C
D
O
S
ABCD
∴ =AB·BC = 4×4 =16
cm
2
解:∵四边形ABCD是平行四边形
∴AC = 2OA,BD = 2OB
∵ △AOB是等边三角形∴OA = OB
∴AC =BD
∴ ABCD是矩形∴∠ ABC=90°
在Rt△ABC中,
∵AB = 4cm,AC=2OA=8cm
∴BC=
应用新知
谢 谢
温故知新
定义:有一个角是直角的平行四边形叫做矩形
矩形性质
角
边
对角线
对称性
四个角都是直角
对边平行且相等
互相平分且相等
中心对称图形,轴对称图形
你知道如何判定一个平行四边形是矩形吗?
矩形的定义:
有一个角是直角的平行四边形是矩形。
你还有其它的判定方法吗?
ABCD
∠A=900
四边形ABCD是矩形
情境一:李芳同学用“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,她说这就是一个矩形,她的判断对吗?为什么?
猜想:有三个角是直角的四边形是矩形 。
你能证明上述结论吗?
请你思考
矩形的判定定理1:
三个角是直角的四边形是矩形 。
A
B
C
D
∵ ∠A=∠B=∠C=90°
∴四边形ABCD是矩形
几何语言:
思考:师傅是怎样知道窗户是矩形的呢?
情境二:工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?
猜想:对角线相等的平行四边形是矩形 。
命题:对角线相等的平行四边形是矩形。
已知:在□ABCD中,AC=BD。
求证:□ABCD是矩形。
A
B
C
D
证明:
∵四边形ABCD是平形四边形
∴ AB=CD,∠ABC+∠DCB=180°
∵ BC=BC, AC=BD
∴ △ABC≌ △DCB(SSS)
∴□ABCD是矩形(有一个角是直角的平行四边形是矩形)
∴ ∠ABC= ∠DCB=90°
对角线相等的平行四边形是矩形 。
矩形的判定定理2:
几何语言:
∵四边形ABCD是平行四边形
AC=BD
∴四边形ABCD是矩形
(对角线相等且互相平分的四边形是矩形。)
A
B
C
D
O
(或OA=OC=OB=OD)
四边形
平行四边形
矩形
有一个角是直角
有三个角是直角
矩形的判定方法:
1.有一个角是直角的平行四边形叫做矩形(定义)
2.三个角是直角的四边形是矩形(判定定理1)
3.对角线相等的平行四边形是矩形(判定定理2)
对角线相等
例1:如图,M为平行四边形ABCD的边AD的中点,且MB=MC,
求证:平行四边形ABCD是矩形。
A
B
C
D
M
证明:∵四边形ABCD是平形四边形
∴ AB=CD, ∠A+∠D=180°
∵ M为AD的中点
∴AM=DM
又 ∵ MB=MC
∴ △ABM≌ △DCM(SSS)
∴ ∠A= ∠D= 90°
∴四边形ABCD是矩形(有一个角是直角的平行四边形是矩形)
例3:已知,如图.矩形ABCD的对角线AC、BD相交于点O,且E、F、G、H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH.
求证:四边形EFGH是矩形.
证明:∵四边形ABCD是矩形
∴AO=BO=CO=DO
∵AE=BF=CG=DH
∴OE=OF=OG=OH
∴四边形EFGH是平行四边形
∵EO+OG=FO+OH 即EG=FH
∴四边形EFGH是矩形(对角线相等的平行四边形是矩形 )
∠A= ∠B= ∠C=90°
ABCD
AC = BD
ABCD
∠A=90°
ABCD
是矩形
四边形ABCD
是矩形
课堂小结
ABCD
是矩形
作业布置(教材106页习题19.1第2、3题)
下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
(5)有三个角是直角的四边形是矩形;
(6)四个角都相等的四边形是矩形;
(7)对角线相等,且有一个角是直角的四边形是矩形;
(10)一组邻边垂直,一组对边平行且相等的四边形是矩形;
(9)对角线相等且互相垂直的四边形是矩形;
(8)一组对角互补的平行四边形是矩形;
(4)有三个角都相等的四边形是矩形;
X
X
X
X
1.对角线相等且一组对边也相等的四边 形是矩形.
2.两条对角线交点到四个顶点距离相等的四边形为矩形.
3.有一组对边相等,一组对角是直角的四边形是矩形.
4.有三个角都相等的四边形是矩形.
判断题
×
√
√
×
巩固新知
5. 具备条件____的四边形是矩形.
A.两条对角线相等 B.对角线互相垂直
C.一组对角是直角 D.有三个角是直角
6. 能够判断一个四边形是矩形的条件是
A.对角线相等 B.对角线垂直
C.对角线互相平分且相等 D.对角线垂直且相等
选择题
C
D
巩固新知
例1 已知□ABCD的对角线AC、BD交于O,△AOB是等边三角形,AB = 4cm,求这个平行四边形的面积.
A
B
C
D
O
S
ABCD
∴ =AB·BC = 4×4 =16
cm
2
解:∵四边形ABCD是平行四边形
∴AC = 2OA,BD = 2OB
∵ △AOB是等边三角形∴OA = OB
∴AC =BD
∴ ABCD是矩形∴∠ ABC=90°
在Rt△ABC中,
∵AB = 4cm,AC=2OA=8cm
∴BC=
应用新知
谢 谢
