2020-2021华东师大版数学九下课堂小练习:第27章《圆》综合题专练(五)(Word版 含解析)
文档属性
| 名称 | 2020-2021华东师大版数学九下课堂小练习:第27章《圆》综合题专练(五)(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 238.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 14:43:19 | ||
图片预览




文档简介
华东师大版数学九年级下册课堂小练习:
第27章《圆》综合题专练(五)
1.如图,已知AB为⊙O的直径,PA与⊙O相切于点A,线段OP与弦AC垂直并相交于点D,OP与弧AC相交于点E,连接BC.
(1)求证:∠PAC=∠B,且PA?BC=AB?CD;
(2)若PA=10,sinP=,求PE的长.
2.已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.
(1)求证:∠BCP=∠BAN
(2)求证:=.
3.已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EH?EA;
(3)若⊙O的半径为5,sinA=,求BH的长.
4.已知AB是圆O的切线,切点为B,直线AO交圆O于C、D两点,CD=2,∠DAB=30°,动点P在直线AB上运动,PC交圆O于另一点Q.
(1)当点P运动到使Q、C两点重合时(如图1),求AP的长;
(2)点P在运动过程中,有几个位置(几种情况)使△CQD的面积为?(直接写出答案)
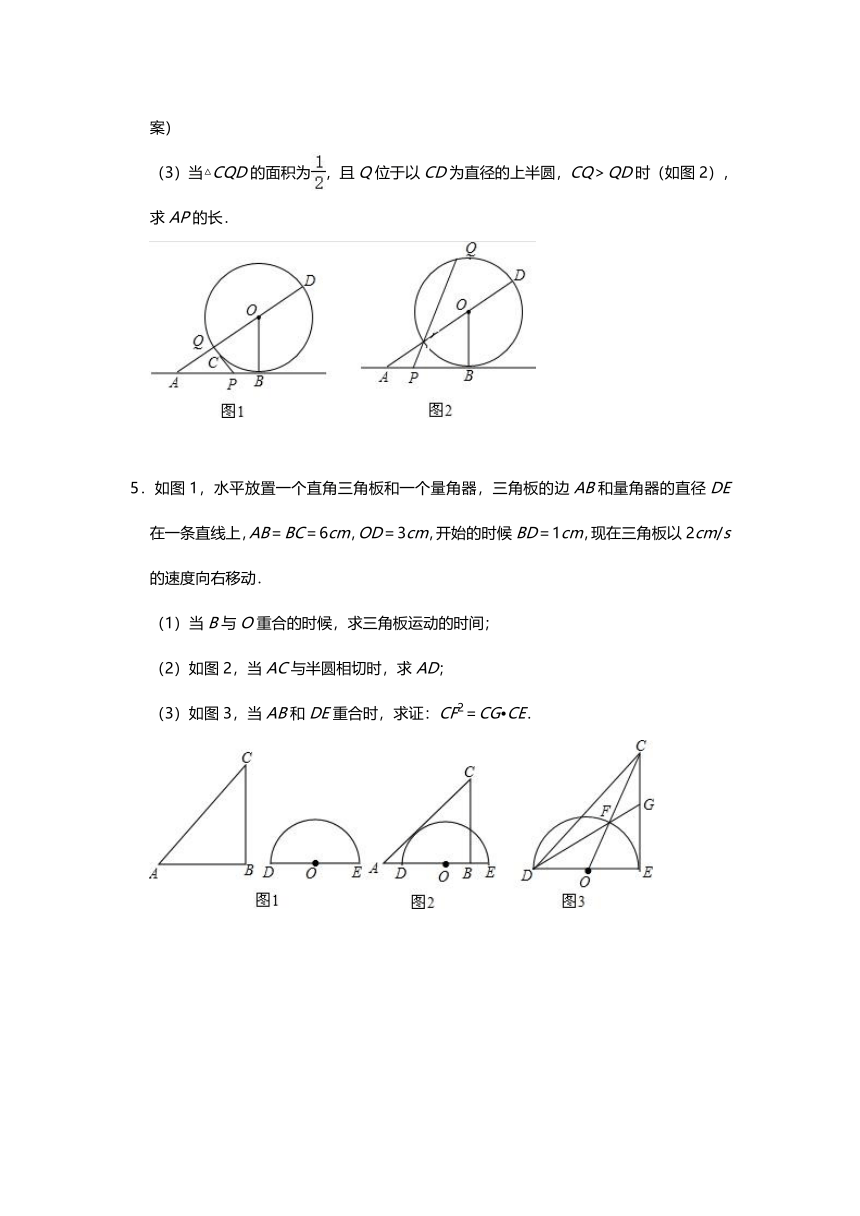
(3)当△CQD的面积为,且Q位于以CD为直径的上半圆,CQ>QD时(如图2),求AP的长.
5.如图1,水平放置一个直角三角板和一个量角器,三角板的边AB和量角器的直径DE在一条直线上,AB=BC=6cm,OD=3cm,开始的时候BD=1cm,现在三角板以2cm/s的速度向右移动.
(1)当B与O重合的时候,求三角板运动的时间;
(2)如图2,当AC与半圆相切时,求AD;
(3)如图3,当AB和DE重合时,求证:CF2=CG?CE.
6.如图,⊙O是△ABC的外接圆,P是⊙O外的一点,AM是⊙O的直径,∠PAC=∠ABC
(1)求证:PA是⊙O的切线;
(2)连接PB与AC交于点D,与⊙O交于点E,F为BD上的一点,若M为的中点,且∠DCF=∠P,求证:==.
7.如图,在直角坐标系中,⊙M经过原点O(0,0),点A(,0)与点B(0,﹣),点D在劣弧上,连接BD交x轴于点C,且∠COD=∠CBO.
(1)求⊙M的半径;
(2)求证:BD平分∠ABO;
(3)在线段BD的延长线上找一点E,使得直线AE恰好为⊙M的切线,求此时点E的坐标.
8.如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA、AO,并延长AO交⊙O于点E,与PB的延长线交于点D.
(1)求证:PA是⊙O的切线;
(2)若=,且OC=4,求PA的长和tanD的值.
9.如图,△ABC中,∠C=90°,点G是线段AC上的一动点(点G不与A、C重合),以AG为直径的⊙O交AB于点D,直线EF垂直平分BD,垂足为F,EF交BC于点E,连结DE.
(1)求证:DE是⊙O的切线;
(2)若cosA=,AB=8,AG=2,求BE的长;
(3)若cosA=,AB=8,直接写出线段BE的取值范围.
10.如图,已知,⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.
(1)求证:AG与⊙O相切.
(2)若AC=6,AB=8,BE=3,求线段OE的长.
参考答案
1.(1)证明:∵PA是⊙O的切线,AB是直径,
∴∠PAO=90°,∠C=90°,
∴∠PAC+∠BAC=90°,∠B+∠BAC=90°,
∴∠PAC=∠B,
又∵OP⊥AC,
∴∠ADP=∠C=90°,
∴△PAD∽△ABC,
∴AP:AB=AD:BC,
∵在⊙O中,AD⊥OD,
∴AD=CD,
∴AP:AB=CD:BC,
∴PA?BC=AB?CD;
(2)解:方法一:
∵sinP=,且AP=10,
∴=,
∴AD=6,
∴AC=2AD=12,
∵在Rt△ADP中,PD==8,
又∵△PAD∽△ABC,
∴AP:AB=PD:AC,
∴AB==15,
∴A0=OE=,
在Rt△APO中,根据勾股定理得:OP==,
∴PE=OP﹣OE=﹣=5.
方法二:
由sinP==,设OA为3x,PO为5x,
由勾股定理得PA为4x,
∵PA=10,∴x=2.5,
∴OA=7.5,OP=12.5,
又∵OE=OA=7.5,
∴PE=OP﹣OE=5.
2.(1)证明:∵AC为⊙O直径,
∴∠ANC=90°,
∴∠NAC+∠ACN=90°,
∵AB=AC,
∴∠BAN=∠CAN,
∵PC是⊙O的切线,
∴∠ACP=90°,
∴∠ACN+∠PCB=90°,
∴∠BCP=∠CAN,
∴∠BCP=∠BAN;
(2)∵AB=AC,
∴∠ABC=∠ACB,
∵∠PBC+∠ABC=∠AMN+∠ACN=180°,
∴∠PBC=∠AMN,
由(1)知∠BCP=∠BAN,
∴△BPC∽△MNA,
∴.
3.(1)证明:∵∠ODB=∠AEC,∠AEC=∠ABC,
∴∠ODB=∠ABC,
∵OF⊥BC,
∴∠BFD=90°,
∴∠ODB+∠DBF=90°,
∴∠ABC+∠DBF=90°,
即∠OBD=90°,
∴BD⊥OB,
∴BD是⊙O的切线;
(2)证明:连接AC,如图1所示:
∵OF⊥BC,
∴,
∴∠CAE=∠ECB,
∵∠CEA=∠HEC,
∴△CEH∽△AEC,
∴,
∴CE2=EH?EA;
(3)解:连接BE,如图2所示:
∵AB是⊙O的直径,
∴∠AEB=90°,
∵⊙O的半径为5,sin∠BAE=,
∴AB=10,BE=AB?sin∠BAE=10×=6,
∴EA===8,
∵,
∴BE=CE=6,
∵CE2=EH?EA,
∴EH==,
在Rt△BEH中,BH===.
4.解:(1)∵AB与⊙O相切于点B,∴∠ABO=90°.
∵∠DAB=30°,OB=CD=×2=1,
∴AO=2OB=2,AC=AO﹣CO=2﹣1=1.
当Q、C两点重合时,CP与⊙O相切于点C,如图1,
则有∠ACP=90°,
∴cos∠CAP===,
解得AP=;
(2)有4个位置使△CQD的面积为.
提示:设点Q到CD的距离为h,
∵S△CQD=CD?h=×2×h=,
∴h=.
由于h=<1,结合图2可得:
有4个位置使△CQD的面积为;
(3)过点Q作QN⊥CD于N,过点P作PM⊥CD于M,如图3.
∵S△CQD=CD?QN=×2×QN=,
∴QN=.
∵CD是⊙O的直径,QN⊥CD,
∴∠CQD=∠QND=∠QNC=90°,
∴∠CQN=90°﹣∠NQD=∠NDQ,
∴△QNC∽△DNQ,
∴=,
∴QN2=CN?DN,
设CN=x,则有=x(2﹣x),
整理得4x2﹣8x+1=0,
解得:x1=,x2=.
∵CQ>QD,∴x=,
∴=2+.
∵QN⊥CD,PM⊥CD,
∴∠PMC=∠QNC=90°.
∵∠MCP=∠NCQ,
∴△PMC∽△QNC,
∴==2+,
∴MC=(2+)MP.
在Rt△AMP中,
tan∠MAP==tan30°=,
∴AM=MP.
∵AC=AM+MC=MP+(2+)MP=1,
∴MP=,
∴AP=2MP=.
5.(1)解:由题意可得:BO=4cm,t==2(s);
(2)解:如图2,连接O与切点H,则OH⊥AC,
又∵∠A=45°,
∴AO=OH=3cm,
∴AD=AO﹣DO=(3﹣3)cm;
(3)证明:如图3,连接EF,
∵OD=OF,
∴∠ODF=∠OFD,
∵DE为直径,
∴∠ODF+∠DEF=90°,
∠DEC=∠DEF+∠CEF=90°,
∴∠CEF=∠ODF=∠OFD=∠CFG,
又∵∠FCG=∠ECF,
∴△CFG∽△CEF,
∴=,
∴CF2=CG?CE.
6.证明:(1)连接CM,
∵∠PAC=∠ABC,∠M=∠ABC,
∴∠PAC=∠M,
∵AM是直径,
∴∠M+∠MAC=90°,
∴∠PAC+∠MAC=90°,
即:∠MAP=90°,
∴MA⊥AP,
∴MA⊥AP,
∴PA是⊙O的切线;
(2)连接AE,
∵M为中点,AM为⊙O的直径,
∴AM⊥BC,
∵AM⊥AP,
∴AP∥BC,
∴△ADP∽△CDB,
∴=,
∵AP∥BC,
∴∠P=∠CBD,
∵∠CBD=∠CAE,
∴∠P=∠DCF,
∴∠DCF=∠CAE,
∵∠ADE=∠CDF,
∴△ADE∽△CDF,
∴=,
∴==.
7.解:(1)∵⊙M经过O、A、B三点,且∠AOB=90°,
∴AB为直径∵点A为(,0),点B为(0,﹣),
∴OA=,OB=,
∴AB==2,
∴⊙M的半径为:;
(2)∵∠COD=∠CBO,∠COD=∠CBA,
∴∠CBO=∠CBA,
即BD平分∠ABO;
(3)如图,过点A作AE⊥AB,垂足为A,交BD的延长线于点E,过点E作EF⊥OA于点F,即AE是切线,
∵在Rt△AOB中,tan∠OAB===,
∴∠OAB=30°,
∴∠ABO=90°﹣∠OAB=60°,
∴∠ABC=∠OBC=∠ABO=30°,
∴OC=OB?tan30°=×=,
∴AC=OA﹣OC=,
∴∠ACE=∠ABC+∠OAB=60°,
∴∠EAC=60°,
∴△ACE是等边三角形,
∴AE=AC=,
∴AF=AE=,EF=AE=,
∴OF=OA﹣AF=,
∴点E的坐标为:(,).
8.(1)证明:连接OB,则OA=OB,
∵OP⊥AB,
∴AC=BC,
∴OP是AB的垂直平分线,
∴PA=PB,
在△PAO和△PBO中,
∵,
∴△PAO≌△PBO(SSS)
∴∠PBO=∠PAO,PB=PA,
∵PB为⊙O的切线,B为切点,
∴∠PBO=90°,
∴∠PAO=90°,
即PA⊥OA,
∴PA是⊙O的切线;
(2)连接BE,
∵=,且OC=4,
∴AC=6,
∴AB=12,
在Rt△ACO中,
由勾股定理得:AO==2,
∴AE=2OA=4,OB=OA=2,
在Rt△APO中,
∵AC⊥OP,
∴AC2=OC?PC,
解得:PC=9,
∴OP=PC+OC=13,
在Rt△APO中,由勾股定理得:AP==3,
∴PB=PA=3,
∵AC=BC,OA=OE,
∴OC=BE,OC∥BE,
∴BE=2OC=8,BE∥OP,
∴△DBE∽△DPO,
∴,
即,
解得:BD=,
在Rt△OBD中,
tan∠D===.
(补充方法:可以证明△DBE∽△DAB,可得===,由此解决问题,可以简单一些)
9.(1)证明:连接OD,如图,
∵△ABC中,∠C=90°,
∴∠A+∠B=90°,
∵直线EF垂直平分BD,
∴ED=EB,
∴∠B=∠EDB,
∵OA=OD,
∴∠A=∠ODA,
∴∠ODA+∠EDB=90°,
∴∠ODE=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)解:连接GD,
∵AG为直径,
∴∠ADG=90°,
∵cosA=,
∴∠A=60°,
∴∠AGD=30°,
∴AD=AG=,
∵AB=8,
∴BD=AB﹣AD=8﹣=7,
∵直线EF垂直平分BD,
∴BF=BD=,
在Rt△BEF中,∠B=30°,
∴EF=BF=,
∴BE=2EF=7;
(3)解:∵cosA=,
∴∠A=60°,
∴∠B=30°,
∴AC=AB=4,
由(2)得AD=AG,
BF=(AB﹣AD)=4﹣AG,
在Rt△BEF中,∠B=30°,
∴EF=BF,
∴BE=2EF=BF=(4﹣AG)=8﹣AG,
∵0<AG<AC,即0<AG<4,
∴6<BE<8.
10.(1)证明:如图,
连接OA,
∵OA=OB,GA=GE
∴∠ABO=∠BAO,∠GEA=∠GAE
∵EF⊥BC,
∴∠BFE=90°,
∴∠ABO+∠BEF=90°,
又∵∠BEF=∠GEA,
∴∠GAE=∠BEF,
∴∠BAO+∠GAE=90°,
即AG与⊙O相切.
(2)解:∵BC为直径,
∴∠BAC=90°,AC=6,AB=8,
∴BC=10,
∵∠EBF=∠CBA,∠BFE=∠BAC,
∴△BEF∽△BCA,
∴==
∴EF=1.8,BF=2.4,
∴OF=OB﹣BF=5﹣2.4=2.6,
∴OE==.
第27章《圆》综合题专练(五)
1.如图,已知AB为⊙O的直径,PA与⊙O相切于点A,线段OP与弦AC垂直并相交于点D,OP与弧AC相交于点E,连接BC.
(1)求证:∠PAC=∠B,且PA?BC=AB?CD;
(2)若PA=10,sinP=,求PE的长.
2.已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.
(1)求证:∠BCP=∠BAN
(2)求证:=.
3.已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EH?EA;
(3)若⊙O的半径为5,sinA=,求BH的长.
4.已知AB是圆O的切线,切点为B,直线AO交圆O于C、D两点,CD=2,∠DAB=30°,动点P在直线AB上运动,PC交圆O于另一点Q.
(1)当点P运动到使Q、C两点重合时(如图1),求AP的长;
(2)点P在运动过程中,有几个位置(几种情况)使△CQD的面积为?(直接写出答案)
(3)当△CQD的面积为,且Q位于以CD为直径的上半圆,CQ>QD时(如图2),求AP的长.
5.如图1,水平放置一个直角三角板和一个量角器,三角板的边AB和量角器的直径DE在一条直线上,AB=BC=6cm,OD=3cm,开始的时候BD=1cm,现在三角板以2cm/s的速度向右移动.
(1)当B与O重合的时候,求三角板运动的时间;
(2)如图2,当AC与半圆相切时,求AD;
(3)如图3,当AB和DE重合时,求证:CF2=CG?CE.
6.如图,⊙O是△ABC的外接圆,P是⊙O外的一点,AM是⊙O的直径,∠PAC=∠ABC
(1)求证:PA是⊙O的切线;
(2)连接PB与AC交于点D,与⊙O交于点E,F为BD上的一点,若M为的中点,且∠DCF=∠P,求证:==.
7.如图,在直角坐标系中,⊙M经过原点O(0,0),点A(,0)与点B(0,﹣),点D在劣弧上,连接BD交x轴于点C,且∠COD=∠CBO.
(1)求⊙M的半径;
(2)求证:BD平分∠ABO;
(3)在线段BD的延长线上找一点E,使得直线AE恰好为⊙M的切线,求此时点E的坐标.
8.如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA、AO,并延长AO交⊙O于点E,与PB的延长线交于点D.
(1)求证:PA是⊙O的切线;
(2)若=,且OC=4,求PA的长和tanD的值.
9.如图,△ABC中,∠C=90°,点G是线段AC上的一动点(点G不与A、C重合),以AG为直径的⊙O交AB于点D,直线EF垂直平分BD,垂足为F,EF交BC于点E,连结DE.
(1)求证:DE是⊙O的切线;
(2)若cosA=,AB=8,AG=2,求BE的长;
(3)若cosA=,AB=8,直接写出线段BE的取值范围.
10.如图,已知,⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.
(1)求证:AG与⊙O相切.
(2)若AC=6,AB=8,BE=3,求线段OE的长.
参考答案
1.(1)证明:∵PA是⊙O的切线,AB是直径,
∴∠PAO=90°,∠C=90°,
∴∠PAC+∠BAC=90°,∠B+∠BAC=90°,
∴∠PAC=∠B,
又∵OP⊥AC,
∴∠ADP=∠C=90°,
∴△PAD∽△ABC,
∴AP:AB=AD:BC,
∵在⊙O中,AD⊥OD,
∴AD=CD,
∴AP:AB=CD:BC,
∴PA?BC=AB?CD;
(2)解:方法一:
∵sinP=,且AP=10,
∴=,
∴AD=6,
∴AC=2AD=12,
∵在Rt△ADP中,PD==8,
又∵△PAD∽△ABC,
∴AP:AB=PD:AC,
∴AB==15,
∴A0=OE=,
在Rt△APO中,根据勾股定理得:OP==,
∴PE=OP﹣OE=﹣=5.
方法二:
由sinP==,设OA为3x,PO为5x,
由勾股定理得PA为4x,
∵PA=10,∴x=2.5,
∴OA=7.5,OP=12.5,
又∵OE=OA=7.5,
∴PE=OP﹣OE=5.
2.(1)证明:∵AC为⊙O直径,
∴∠ANC=90°,
∴∠NAC+∠ACN=90°,
∵AB=AC,
∴∠BAN=∠CAN,
∵PC是⊙O的切线,
∴∠ACP=90°,
∴∠ACN+∠PCB=90°,
∴∠BCP=∠CAN,
∴∠BCP=∠BAN;
(2)∵AB=AC,
∴∠ABC=∠ACB,
∵∠PBC+∠ABC=∠AMN+∠ACN=180°,
∴∠PBC=∠AMN,
由(1)知∠BCP=∠BAN,
∴△BPC∽△MNA,
∴.
3.(1)证明:∵∠ODB=∠AEC,∠AEC=∠ABC,
∴∠ODB=∠ABC,
∵OF⊥BC,
∴∠BFD=90°,
∴∠ODB+∠DBF=90°,
∴∠ABC+∠DBF=90°,
即∠OBD=90°,
∴BD⊥OB,
∴BD是⊙O的切线;
(2)证明:连接AC,如图1所示:
∵OF⊥BC,
∴,
∴∠CAE=∠ECB,
∵∠CEA=∠HEC,
∴△CEH∽△AEC,
∴,
∴CE2=EH?EA;
(3)解:连接BE,如图2所示:
∵AB是⊙O的直径,
∴∠AEB=90°,
∵⊙O的半径为5,sin∠BAE=,
∴AB=10,BE=AB?sin∠BAE=10×=6,
∴EA===8,
∵,
∴BE=CE=6,
∵CE2=EH?EA,
∴EH==,
在Rt△BEH中,BH===.
4.解:(1)∵AB与⊙O相切于点B,∴∠ABO=90°.
∵∠DAB=30°,OB=CD=×2=1,
∴AO=2OB=2,AC=AO﹣CO=2﹣1=1.
当Q、C两点重合时,CP与⊙O相切于点C,如图1,
则有∠ACP=90°,
∴cos∠CAP===,
解得AP=;
(2)有4个位置使△CQD的面积为.
提示:设点Q到CD的距离为h,
∵S△CQD=CD?h=×2×h=,
∴h=.
由于h=<1,结合图2可得:
有4个位置使△CQD的面积为;
(3)过点Q作QN⊥CD于N,过点P作PM⊥CD于M,如图3.
∵S△CQD=CD?QN=×2×QN=,
∴QN=.
∵CD是⊙O的直径,QN⊥CD,
∴∠CQD=∠QND=∠QNC=90°,
∴∠CQN=90°﹣∠NQD=∠NDQ,
∴△QNC∽△DNQ,
∴=,
∴QN2=CN?DN,
设CN=x,则有=x(2﹣x),
整理得4x2﹣8x+1=0,
解得:x1=,x2=.
∵CQ>QD,∴x=,
∴=2+.
∵QN⊥CD,PM⊥CD,
∴∠PMC=∠QNC=90°.
∵∠MCP=∠NCQ,
∴△PMC∽△QNC,
∴==2+,
∴MC=(2+)MP.
在Rt△AMP中,
tan∠MAP==tan30°=,
∴AM=MP.
∵AC=AM+MC=MP+(2+)MP=1,
∴MP=,
∴AP=2MP=.
5.(1)解:由题意可得:BO=4cm,t==2(s);
(2)解:如图2,连接O与切点H,则OH⊥AC,
又∵∠A=45°,
∴AO=OH=3cm,
∴AD=AO﹣DO=(3﹣3)cm;
(3)证明:如图3,连接EF,
∵OD=OF,
∴∠ODF=∠OFD,
∵DE为直径,
∴∠ODF+∠DEF=90°,
∠DEC=∠DEF+∠CEF=90°,
∴∠CEF=∠ODF=∠OFD=∠CFG,
又∵∠FCG=∠ECF,
∴△CFG∽△CEF,
∴=,
∴CF2=CG?CE.
6.证明:(1)连接CM,
∵∠PAC=∠ABC,∠M=∠ABC,
∴∠PAC=∠M,
∵AM是直径,
∴∠M+∠MAC=90°,
∴∠PAC+∠MAC=90°,
即:∠MAP=90°,
∴MA⊥AP,
∴MA⊥AP,
∴PA是⊙O的切线;
(2)连接AE,
∵M为中点,AM为⊙O的直径,
∴AM⊥BC,
∵AM⊥AP,
∴AP∥BC,
∴△ADP∽△CDB,
∴=,
∵AP∥BC,
∴∠P=∠CBD,
∵∠CBD=∠CAE,
∴∠P=∠DCF,
∴∠DCF=∠CAE,
∵∠ADE=∠CDF,
∴△ADE∽△CDF,
∴=,
∴==.
7.解:(1)∵⊙M经过O、A、B三点,且∠AOB=90°,
∴AB为直径∵点A为(,0),点B为(0,﹣),
∴OA=,OB=,
∴AB==2,
∴⊙M的半径为:;
(2)∵∠COD=∠CBO,∠COD=∠CBA,
∴∠CBO=∠CBA,
即BD平分∠ABO;
(3)如图,过点A作AE⊥AB,垂足为A,交BD的延长线于点E,过点E作EF⊥OA于点F,即AE是切线,
∵在Rt△AOB中,tan∠OAB===,
∴∠OAB=30°,
∴∠ABO=90°﹣∠OAB=60°,
∴∠ABC=∠OBC=∠ABO=30°,
∴OC=OB?tan30°=×=,
∴AC=OA﹣OC=,
∴∠ACE=∠ABC+∠OAB=60°,
∴∠EAC=60°,
∴△ACE是等边三角形,
∴AE=AC=,
∴AF=AE=,EF=AE=,
∴OF=OA﹣AF=,
∴点E的坐标为:(,).
8.(1)证明:连接OB,则OA=OB,
∵OP⊥AB,
∴AC=BC,
∴OP是AB的垂直平分线,
∴PA=PB,
在△PAO和△PBO中,
∵,
∴△PAO≌△PBO(SSS)
∴∠PBO=∠PAO,PB=PA,
∵PB为⊙O的切线,B为切点,
∴∠PBO=90°,
∴∠PAO=90°,
即PA⊥OA,
∴PA是⊙O的切线;
(2)连接BE,
∵=,且OC=4,
∴AC=6,
∴AB=12,
在Rt△ACO中,
由勾股定理得:AO==2,
∴AE=2OA=4,OB=OA=2,
在Rt△APO中,
∵AC⊥OP,
∴AC2=OC?PC,
解得:PC=9,
∴OP=PC+OC=13,
在Rt△APO中,由勾股定理得:AP==3,
∴PB=PA=3,
∵AC=BC,OA=OE,
∴OC=BE,OC∥BE,
∴BE=2OC=8,BE∥OP,
∴△DBE∽△DPO,
∴,
即,
解得:BD=,
在Rt△OBD中,
tan∠D===.
(补充方法:可以证明△DBE∽△DAB,可得===,由此解决问题,可以简单一些)
9.(1)证明:连接OD,如图,
∵△ABC中,∠C=90°,
∴∠A+∠B=90°,
∵直线EF垂直平分BD,
∴ED=EB,
∴∠B=∠EDB,
∵OA=OD,
∴∠A=∠ODA,
∴∠ODA+∠EDB=90°,
∴∠ODE=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)解:连接GD,
∵AG为直径,
∴∠ADG=90°,
∵cosA=,
∴∠A=60°,
∴∠AGD=30°,
∴AD=AG=,
∵AB=8,
∴BD=AB﹣AD=8﹣=7,
∵直线EF垂直平分BD,
∴BF=BD=,
在Rt△BEF中,∠B=30°,
∴EF=BF=,
∴BE=2EF=7;
(3)解:∵cosA=,
∴∠A=60°,
∴∠B=30°,
∴AC=AB=4,
由(2)得AD=AG,
BF=(AB﹣AD)=4﹣AG,
在Rt△BEF中,∠B=30°,
∴EF=BF,
∴BE=2EF=BF=(4﹣AG)=8﹣AG,
∵0<AG<AC,即0<AG<4,
∴6<BE<8.
10.(1)证明:如图,
连接OA,
∵OA=OB,GA=GE
∴∠ABO=∠BAO,∠GEA=∠GAE
∵EF⊥BC,
∴∠BFE=90°,
∴∠ABO+∠BEF=90°,
又∵∠BEF=∠GEA,
∴∠GAE=∠BEF,
∴∠BAO+∠GAE=90°,
即AG与⊙O相切.
(2)解:∵BC为直径,
∴∠BAC=90°,AC=6,AB=8,
∴BC=10,
∵∠EBF=∠CBA,∠BFE=∠BAC,
∴△BEF∽△BCA,
∴==
∴EF=1.8,BF=2.4,
∴OF=OB﹣BF=5﹣2.4=2.6,
∴OE==.
