高中数学人教A版必修三3.3.1 几何概型 课件(30张PPT)
文档属性
| 名称 | 高中数学人教A版必修三3.3.1 几何概型 课件(30张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 736.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 00:00:00 | ||
图片预览








文档简介
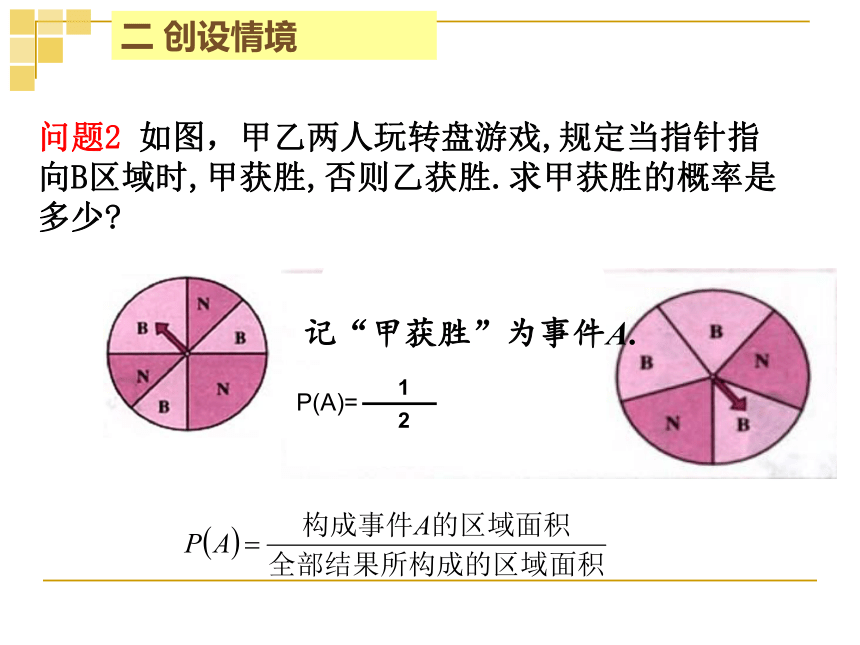
古典概型:(1)试验中所有可能出现的基本事件
只有有限个
(2)每个基本事件出现的可能性相等.
我们将具有以上两个特点的概率模型称
为古典概率模型,简称古典概型.
P(A)=
A包含的基本事件的个数
基本事件的总数
概率计算公式:
一 复习回顾
我抛一块硬币,猜这一次是正面向上。
问题:抛一次硬币,正面
向上的概率是多少?
这是什么概型问题,它是如何定义的?
取一根长度为3m的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不小于1m的概率有多大?
思考:上述实验的基本事件是什么?
上述概率问题是古典概型问题吗?为什么?
二 创设情境
几何概型
问题1
解:记“剪得两段的长度都不小于1m”
为事件A.
取一根长度为3m的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不小于1m的概率有多大?
二 创设情境
把绳子分为三个区域,于是当剪断位置处在中间一段上时,
事件A发生.由于绳子上各点被剪断是等可能的
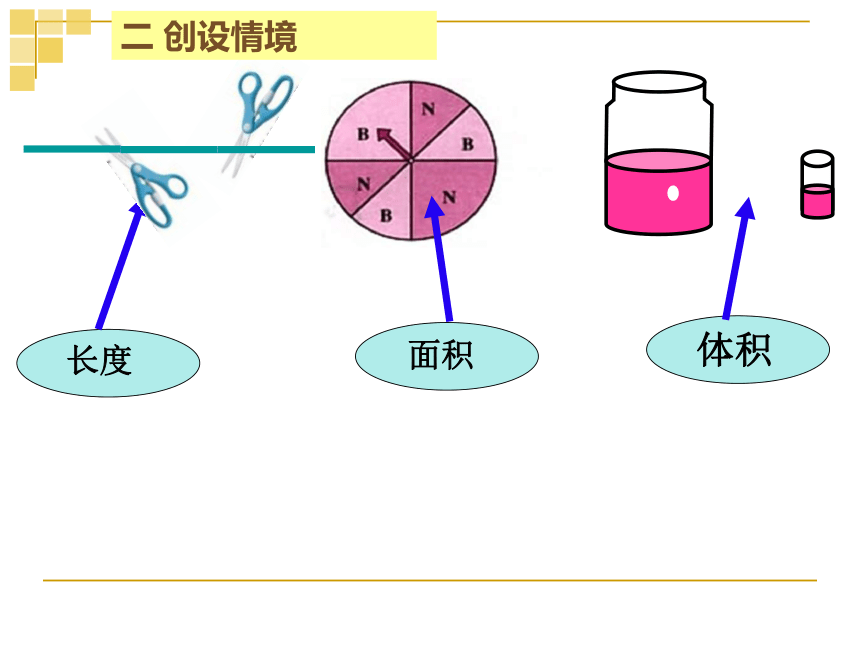
问题2 如图,甲乙两人玩转盘游戏,规定当指针指向B区域时,甲获胜,否则乙获胜.求甲获胜的概率是多少?
记“甲获胜”为事件A.
二 创设情境
P(A)=
1
2
有一杯1升的水, 其中含有1个草履虫, 用一个小杯从这杯水中取出0.1升, 求小杯水中含有这个草履虫的概率.
问题3
二 创设情境
记“含有草履虫”为事件A.
P(A)= =
0.1
1
1
10
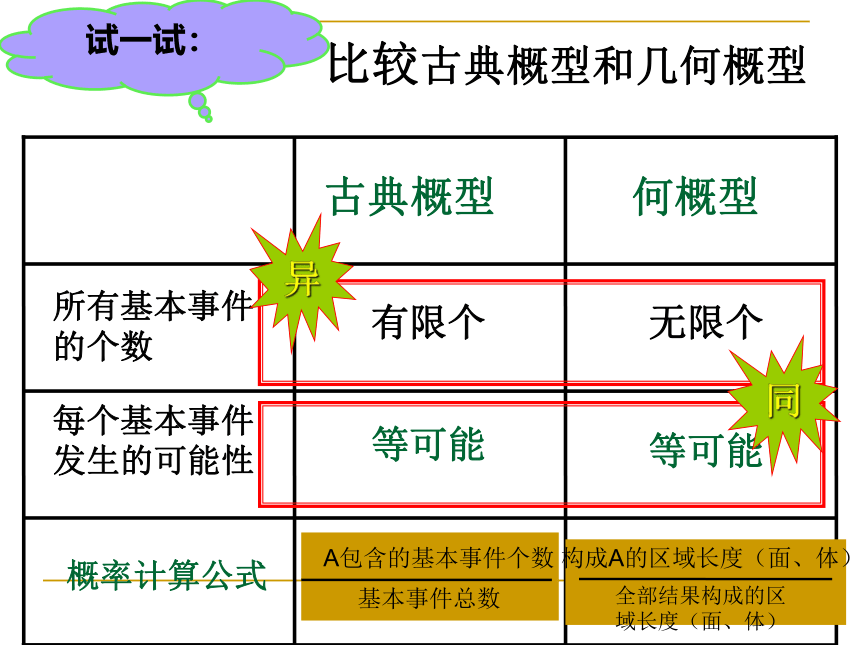
长度
面积
体积
二 创设情境
定义:如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称几何概型。
几何概型:
几何概型的公式:
特点:
(1)试验中所有可能出现的基本事件有无限多个
(2)每个基本事件出现的可能性相等
三 建构概念
比较古典概型和几何概型
古典概型
几何概型
所有基本事件的个数
每个基本事件发生的可能性
概率计算公式
有限个
无限个
等可能
等可能
试一试:
异
同
A包含的基本事件个数
基本事件总数
构成A的区域长度(面、体)
全部结果构成的区域长度(面、体)
例1.在区间[1,3] 上任取一个数,则这个数大于1.5的概率为( )
A 0.25 B 0.5 C 0.6 D 0.75
D
四 尝试运用
2. 在1万平方千米的海域中有40平方千米的大陆架储藏着石油,如果在海域中任意点钻探,钻到油层面的概率 .
0.004
例2. 某人午觉醒来,发现表停了,他打开收音机,想听电台报时,求他等待的时间不多于10分钟的概率.
分析: 收音机每小时报时一次,他在0~60分钟之间任何 一个时刻打开收音机是等可能的, 0~60分钟之间有无穷个时刻,符合几何概型条件.
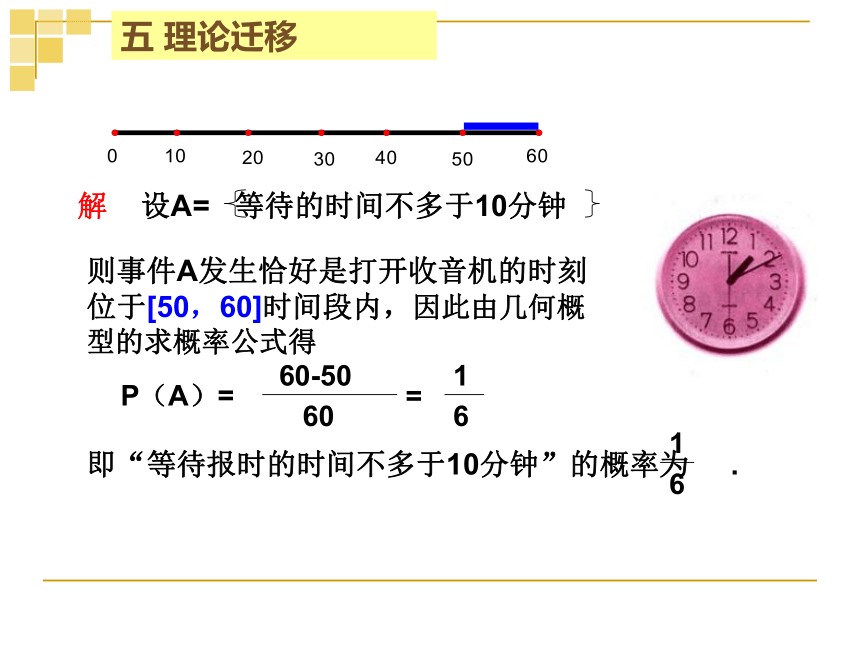
五 理论迁移
把时刻抽象为点,时间抽象为线段,故可以用几何概型求解.
则事件A发生恰好是打开收音机的时刻位于[50,60]时间段内,因此由几何概型的求概率公式得
P(A)=
60-50
60
=
1
6
即“等待报时的时间不多于10分钟”的概率为 .
1
6
解 设A= 等待的时间不多于10分钟
五 理论迁移
五 理论迁移
例2. 某人午觉醒来,发现表停了,他打开收音机,想听电台报时,求他等待的时间不多于10分钟的概率.
分析: 收音机每小时报时一次,他在0~60分钟之间任何 一个时刻打开收音机是等可能的, 0~60分钟之间有无穷个时刻,符合几何概型条件.
法二:(利用[50,60]时间段所占的面积):
法三:(利用利用[50,60]时间段所占的弧长):
法四:(利用[50,60]时间段所占的圆心角):
几何概型并不是只研究与几何图形有关的概率模型,实际上有的例子与几何图形没有直接的关系,而是通过去合理的抽象转化,用何图形去解决问题。
因此很多与实际生活有关的概率问题,只要满足几何概型的两个特点,都可以用几何概型去刻画
五 理论迁移
与长度有关的几何概型问题
六 典例分类
C
与面积有关的几何概型问题
六 典例分类
B
2.在一个边长为2的正方形中有一个椭圆(如图),随机向正方形内丢一粒豆子,若落入椭圆的概率为0.3, 求椭圆的面积 .
1.2.
六 典例分类
六 典例分类
六 典例分类
3.几何概型的概率计算公式
1.几何概型的特征
2.几何概型的定义
每个基本事件出现的可能性 .
几何概型中所有可能出现的基本事件有 个;
如果某个事件发生的概率只与构成该事件区域的几何度量(长度、面积或 体积)成正比例,则称这样的概率模型为几何概率模型。
无限
相等
4 .解决几何概型的关键是抽象出随机事件对应的几何图形.
八 我的收获
七 深化提高
七 深化提高
1. P142 A组 1、2、3题
2.练习册 课时演练
九、课堂作业
例2 假设你家订了一份报纸,送报人可能在早
上6:30—7:30之间把报纸送到你家,你父亲离开家去工作的时间在早上7:00—8:00之间,问你父亲在离开家前能得到报纸(称为事件A)的概率是多少?
五 理论迁移
解:以横坐标X表示报纸送到时间,以纵坐标
Y表示父亲离家时间建立平面直角坐标
系,假设随机试验落在方形区域内任何一
点是等可能的,所以符合几何概型的条件.
根据题意,只要点落到阴影部
分,就表示父亲在离开家前能
得到报纸,即时间A发生,所以
五 理论迁移
1.甲、乙二人约定在下午12点到17点之间在某地会面,先到者等一个小时后即离去,设二人在这段时间内的各时刻到达是等可能的,且二人互不影响。求二人能会面的概率。
解: 以 X , Y 分别表示甲、乙二人到达的时刻,于是
即 点 M 落在图中的阴影部
分.所有的点构成一个正
方形,即有无穷多个结果.
由于每人在任一时刻到达
都是等可能的,所以落在正
方形内各点是等可能的.
.M(X,Y)
y
5
4
3
2
1
0 1 2 3 4 5
x
六 提升训练
二人会面当且仅当:
0 1 2 3 4 5
x
y
5
4
3
2
1
y=x -1
y=x+1
记“两人会面”为事件A
六 提升训练
二、与面积有关的几何概型问题
例1.在区间[1,3] 上任取一个数,则这个数大于1.5的概率为( )
A 0.25 B 0.5 C 0.6 D 0.75
一、与长度有关的几何概型问题
三、与体积有关的几何概型问题
D
四 尝试运用
3.一只小蜜蜂在一个棱长为3的正方体内自由飞行,若蜜蜂在飞行过程中始终保持与正方体6个面的距离均大于1,称其为“安全飞行”,则蜜蜂“安全飞行”的概率
1
27
2. 在1万平方千米的海域中有40平方千米的大陆架储藏着石油,如果在海域中任意点钻探,钻到油层面的概率 .
0.004
几何概型并不是只研究与几何图形有关的概率模型,实际上有的例子与几何图形没有直接的关系,而是通过去合理的抽象转化,用何图形去解决问题。
因此很多与实际生活有关的概率问题,只要满足几何概型的两个特点,都可以用几何概型去刻画
抽象为几何 图形
计算几何度量
求概率
下结论
记事件
五 理论迁移
六 典例分类
只有有限个
(2)每个基本事件出现的可能性相等.
我们将具有以上两个特点的概率模型称
为古典概率模型,简称古典概型.
P(A)=
A包含的基本事件的个数
基本事件的总数
概率计算公式:
一 复习回顾
我抛一块硬币,猜这一次是正面向上。
问题:抛一次硬币,正面
向上的概率是多少?
这是什么概型问题,它是如何定义的?
取一根长度为3m的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不小于1m的概率有多大?
思考:上述实验的基本事件是什么?
上述概率问题是古典概型问题吗?为什么?
二 创设情境
几何概型
问题1
解:记“剪得两段的长度都不小于1m”
为事件A.
取一根长度为3m的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不小于1m的概率有多大?
二 创设情境
把绳子分为三个区域,于是当剪断位置处在中间一段上时,
事件A发生.由于绳子上各点被剪断是等可能的
问题2 如图,甲乙两人玩转盘游戏,规定当指针指向B区域时,甲获胜,否则乙获胜.求甲获胜的概率是多少?
记“甲获胜”为事件A.
二 创设情境
P(A)=
1
2
有一杯1升的水, 其中含有1个草履虫, 用一个小杯从这杯水中取出0.1升, 求小杯水中含有这个草履虫的概率.
问题3
二 创设情境
记“含有草履虫”为事件A.
P(A)= =
0.1
1
1
10
长度
面积
体积
二 创设情境
定义:如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称几何概型。
几何概型:
几何概型的公式:
特点:
(1)试验中所有可能出现的基本事件有无限多个
(2)每个基本事件出现的可能性相等
三 建构概念
比较古典概型和几何概型
古典概型
几何概型
所有基本事件的个数
每个基本事件发生的可能性
概率计算公式
有限个
无限个
等可能
等可能
试一试:
异
同
A包含的基本事件个数
基本事件总数
构成A的区域长度(面、体)
全部结果构成的区域长度(面、体)
例1.在区间[1,3] 上任取一个数,则这个数大于1.5的概率为( )
A 0.25 B 0.5 C 0.6 D 0.75
D
四 尝试运用
2. 在1万平方千米的海域中有40平方千米的大陆架储藏着石油,如果在海域中任意点钻探,钻到油层面的概率 .
0.004
例2. 某人午觉醒来,发现表停了,他打开收音机,想听电台报时,求他等待的时间不多于10分钟的概率.
分析: 收音机每小时报时一次,他在0~60分钟之间任何 一个时刻打开收音机是等可能的, 0~60分钟之间有无穷个时刻,符合几何概型条件.
五 理论迁移
把时刻抽象为点,时间抽象为线段,故可以用几何概型求解.
则事件A发生恰好是打开收音机的时刻位于[50,60]时间段内,因此由几何概型的求概率公式得
P(A)=
60-50
60
=
1
6
即“等待报时的时间不多于10分钟”的概率为 .
1
6
解 设A= 等待的时间不多于10分钟
五 理论迁移
五 理论迁移
例2. 某人午觉醒来,发现表停了,他打开收音机,想听电台报时,求他等待的时间不多于10分钟的概率.
分析: 收音机每小时报时一次,他在0~60分钟之间任何 一个时刻打开收音机是等可能的, 0~60分钟之间有无穷个时刻,符合几何概型条件.
法二:(利用[50,60]时间段所占的面积):
法三:(利用利用[50,60]时间段所占的弧长):
法四:(利用[50,60]时间段所占的圆心角):
几何概型并不是只研究与几何图形有关的概率模型,实际上有的例子与几何图形没有直接的关系,而是通过去合理的抽象转化,用何图形去解决问题。
因此很多与实际生活有关的概率问题,只要满足几何概型的两个特点,都可以用几何概型去刻画
五 理论迁移
与长度有关的几何概型问题
六 典例分类
C
与面积有关的几何概型问题
六 典例分类
B
2.在一个边长为2的正方形中有一个椭圆(如图),随机向正方形内丢一粒豆子,若落入椭圆的概率为0.3, 求椭圆的面积 .
1.2.
六 典例分类
六 典例分类
六 典例分类
3.几何概型的概率计算公式
1.几何概型的特征
2.几何概型的定义
每个基本事件出现的可能性 .
几何概型中所有可能出现的基本事件有 个;
如果某个事件发生的概率只与构成该事件区域的几何度量(长度、面积或 体积)成正比例,则称这样的概率模型为几何概率模型。
无限
相等
4 .解决几何概型的关键是抽象出随机事件对应的几何图形.
八 我的收获
七 深化提高
七 深化提高
1. P142 A组 1、2、3题
2.练习册 课时演练
九、课堂作业
例2 假设你家订了一份报纸,送报人可能在早
上6:30—7:30之间把报纸送到你家,你父亲离开家去工作的时间在早上7:00—8:00之间,问你父亲在离开家前能得到报纸(称为事件A)的概率是多少?
五 理论迁移
解:以横坐标X表示报纸送到时间,以纵坐标
Y表示父亲离家时间建立平面直角坐标
系,假设随机试验落在方形区域内任何一
点是等可能的,所以符合几何概型的条件.
根据题意,只要点落到阴影部
分,就表示父亲在离开家前能
得到报纸,即时间A发生,所以
五 理论迁移
1.甲、乙二人约定在下午12点到17点之间在某地会面,先到者等一个小时后即离去,设二人在这段时间内的各时刻到达是等可能的,且二人互不影响。求二人能会面的概率。
解: 以 X , Y 分别表示甲、乙二人到达的时刻,于是
即 点 M 落在图中的阴影部
分.所有的点构成一个正
方形,即有无穷多个结果.
由于每人在任一时刻到达
都是等可能的,所以落在正
方形内各点是等可能的.
.M(X,Y)
y
5
4
3
2
1
0 1 2 3 4 5
x
六 提升训练
二人会面当且仅当:
0 1 2 3 4 5
x
y
5
4
3
2
1
y=x -1
y=x+1
记“两人会面”为事件A
六 提升训练
二、与面积有关的几何概型问题
例1.在区间[1,3] 上任取一个数,则这个数大于1.5的概率为( )
A 0.25 B 0.5 C 0.6 D 0.75
一、与长度有关的几何概型问题
三、与体积有关的几何概型问题
D
四 尝试运用
3.一只小蜜蜂在一个棱长为3的正方体内自由飞行,若蜜蜂在飞行过程中始终保持与正方体6个面的距离均大于1,称其为“安全飞行”,则蜜蜂“安全飞行”的概率
1
27
2. 在1万平方千米的海域中有40平方千米的大陆架储藏着石油,如果在海域中任意点钻探,钻到油层面的概率 .
0.004
几何概型并不是只研究与几何图形有关的概率模型,实际上有的例子与几何图形没有直接的关系,而是通过去合理的抽象转化,用何图形去解决问题。
因此很多与实际生活有关的概率问题,只要满足几何概型的两个特点,都可以用几何概型去刻画
抽象为几何 图形
计算几何度量
求概率
下结论
记事件
五 理论迁移
六 典例分类
