2020-2021学年苏科版九年级数学下册 第6章 图形的相似 单元检测试题(word版,有答案)
文档属性
| 名称 | 2020-2021学年苏科版九年级数学下册 第6章 图形的相似 单元检测试题(word版,有答案) |  | |
| 格式 | docx | ||
| 文件大小 | 223.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 15:38:08 | ||
图片预览

文档简介
1049020010693400123190000第6章 图形的相似 单元检测试题
(满分120分;时间:90分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
1. 已知四条线段a、b、c、d依次成比例,且a=1,b=3,c=3,则d=( ? ? ??)
A.3 B.6 C.8 D.9
?
2. 如果2a=5b,那么下列比例式中正确的是(? ? ? ? )
A.ab=25 B.a5=2b C.ab=52 D.a2=b5
?
3. 已知点C是线段AB的黄金分割点,且AC>BC,AB=2,则AC为( )
A.5-1 B.3-5 C.5-12 D.0.618
?
4. 点D是线段AB的黄金分割点(AD>BD),若AB=2,则BD=(? ? ? ? )
A.5-12 B.3-52 C.5-1 D.3-5
?
5. 下列结论错误的是( )
A.所有的正方形都相似 B.所有的等边三角形都相似
C.所有的菱形都相似 D.所有的正六边形都相似
?
6. 若ab=38,则aa+b的值是( )
A.811 B.613 C.311 D.35
?
7. 如图L1?//L2?//L3,AB=4,DE=3,EF=6,则BC的长( )
A.4 B.6 C.8 D.10
?
8. 下列语句正确的是( )
A.有一个角对应相等的两个直角三角形相似
B.如果两个图形位似,那么对应线段平行或在同一条直线直线上
C.两个矩形一定相似
D.如果将一个三角形的各边长都扩大二倍,则其面积将扩大4倍
?
9. 如图,AD?//?BE?//?CF,直线m,n与这三条平行线分别交于点A、B、C和点D、E、F,已知AB=5,BC=10,DE=4,则EF的长为( )
A.12.5 B.12 C.8 D.4
?
10. 如图,AB与CD相交于点E,AD?//?BC,BEAE=35,CD=16,则DE的长为( )
A.3 B.6 C.485 D.10
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
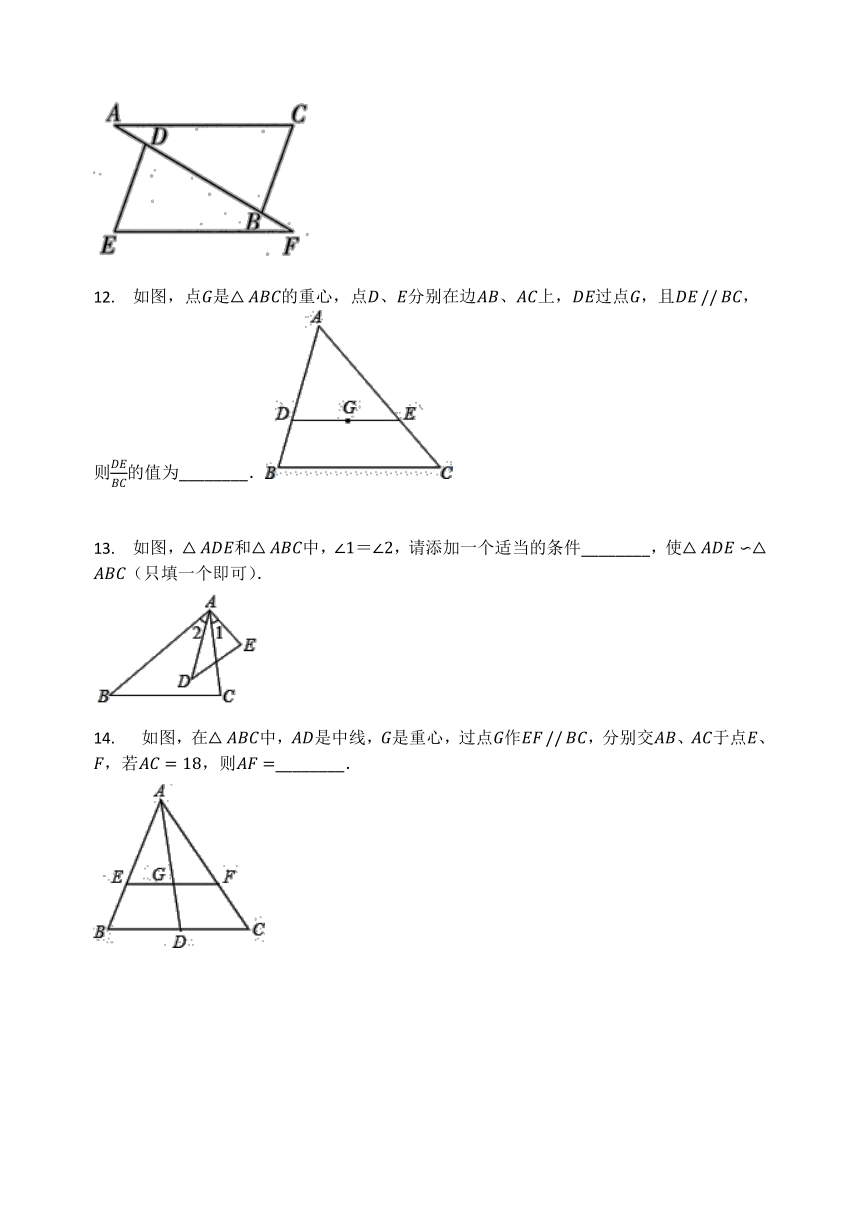
11. 如图,点A,D,B,F在一条直线上,AC=EF,AD=FB,要使△ABC?△FDE,需添加的条件是________(填一个即可).
?
12. 如图,点G是△ABC的重心,点D、E分别在边AB、AC上,DE过点G,且DE?//?BC,则DEBC的值为________.
?
13. 如图,△ADE和△ABC中,∠1=∠2,请添加一个适当的条件________,使△ADE∽△ABC(只填一个即可).
?
14. 如图,在△ABC中,AD是中线,G是重心,过点G作EF?//?BC,分别交AB、AC于点E、F,若AC=18,则AF=________.
?
15. 如图,若△ABC∽△DEF,则∠D的度数为________.
?
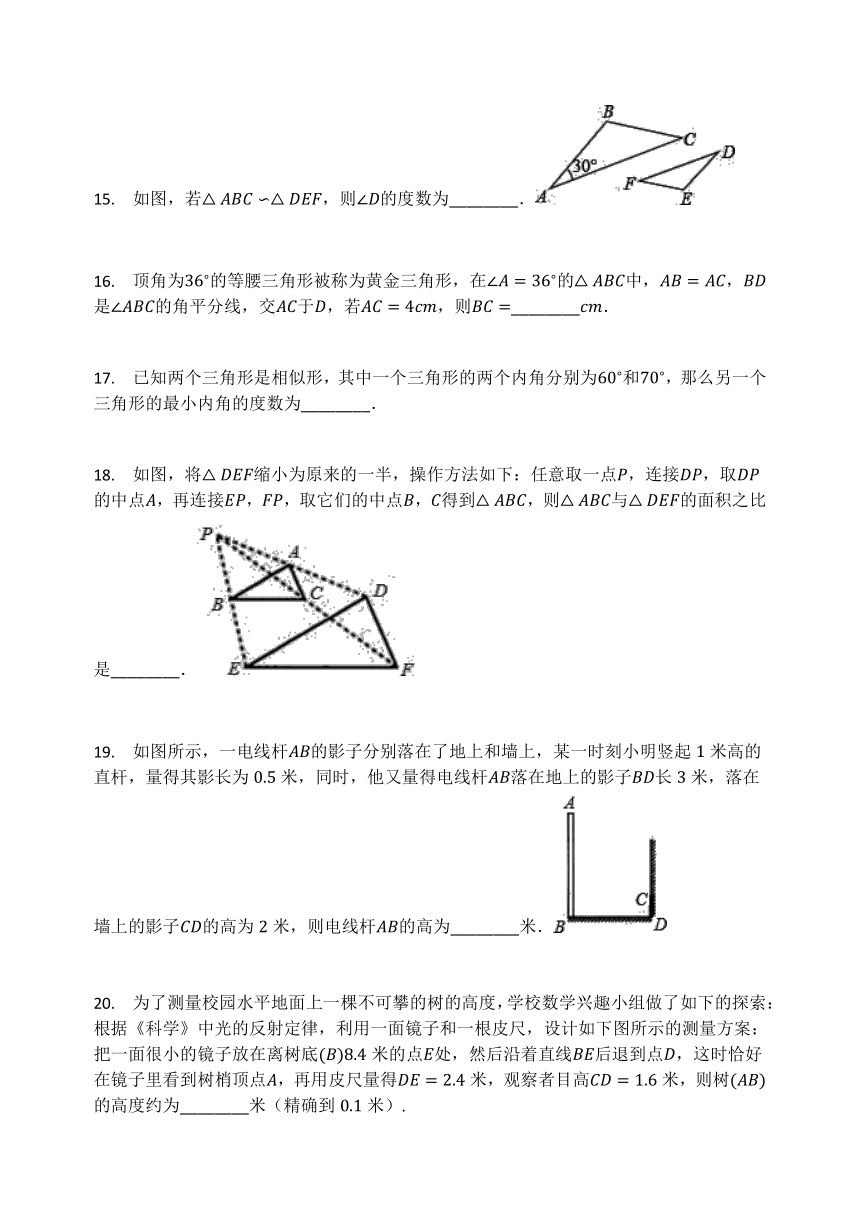
16. 顶角为36?的等腰三角形被称为黄金三角形,在∠A=36?的△ABC中,AB=AC,BD是∠ABC的角平分线,交AC于D,若AC=4cm,则BC=________cm.
?
17. 已知两个三角形是相似形,其中一个三角形的两个内角分别为60?和70?,那么另一个三角形的最小内角的度数为________.
?
18. 如图,将△DEF缩小为原来的一半,操作方法如下:任意取一点P,连接DP,取DP的中点A,再连接EP,FP,取它们的中点B,C得到△ABC,则△ABC与△DEF的面积之比是________.
?
19. 如图所示,一电线杆AB的影子分别落在了地上和墙上,某一时刻小明竖起1米高的直杆,量得其影长为0.5米,同时,他又量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米,则电线杆AB的高为________米.
?
20. 为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索:根据《科学》中光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子放在离树底(B)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.4米,观察者目高CD=1.6米,则树(AB)的高度约为________米(精确到0.1米).
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
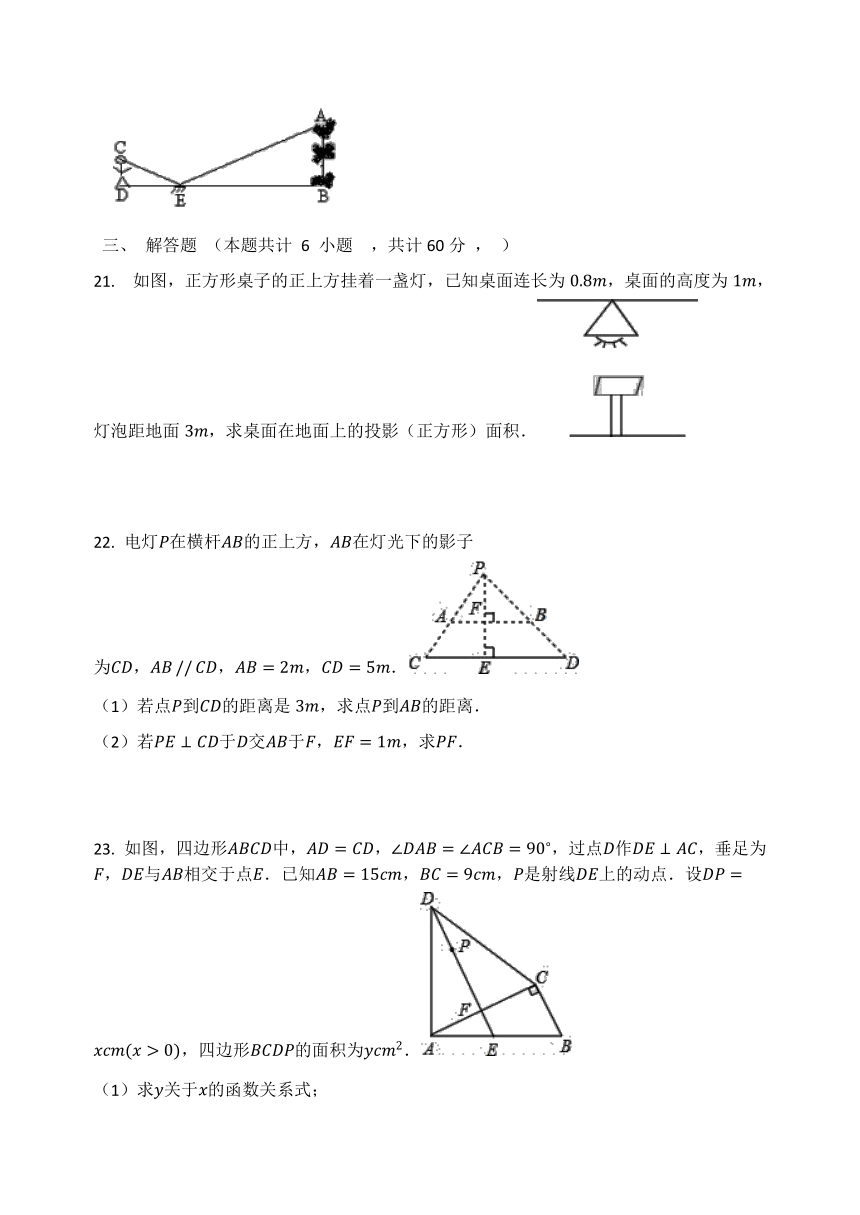
21. 如图,正方形桌子的正上方挂着一盏灯,已知桌面连长为0.8m,桌面的高度为1m,灯泡距地面3m,求桌面在地面上的投影(正方形)面积.
?
22. 电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB?//?CD,AB=2m,CD=5m.
(1)若点P到CD的距离是3m,求点P到AB的距离.
(2)若PE⊥CD于D交AB于F,EF=1m,求PF.
?
23. 如图,四边形ABCD中,AD=CD,∠DAB=∠ACB=90?,过点D作DE⊥AC,垂足为F,DE与AB相交于点E.已知AB=15cm,BC=9cm,P是射线DE上的动点.设DP=xcm(x>0),四边形BCDP的面积为ycm2.
(1)求y关于x的函数关系式;
(2)当x为何值时,△PBC的周长最小,并求出此时y的值.
?
24. 如图(1),在矩形ABCD中,AD=6,AB=8,点E是AB边上-动点(点E不与点A、B重合),过点E作EF?//?AC交BC于点F,连接ED.
(1)设AE=x,则EF=________;
(2)若DE⊥EF,求EF的长;
(3)如图(2),过点E作EG⊥EF.交AC于点H,交直线CD于点G,连接AG、FG,随着点E在线段AB上的运动,当AE为何值时,△EFG与△AHE相似?
?
25. 如图1,正方形ABCD和正方形AEFG,连接DG,BE.
(1)发现:当正方形AEFG绕点A旋转,如图2,①线段DG与BE之间的数量关系是 ?? ;②直线DG与直线BE之间的位置关系是 ?? .
(2)探究:如图3,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE,证明:直线DG⊥BE.
(3)应用:在(2)情况下,连结GE(点E在AB上方),若GE?//?AB,且AB=,AE=1,则线段DG是多少?(直接写出结论)
?
参考答案与试题解析
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
D
【解答】
解:根据题意得:ab=cd,即13=3d,
解得:d=9.
故选D.
2.
【答案】
C
【解答】
解:两边同除以2b得:ab=52,C正确,
其他等式均无法得到.
故选C.
3.
【答案】
A
【解答】
解:∵ 点C是线段AB的黄金分割点,且AC>BC,
∴ AC=5-12AB,
而AB=2,
∴ AC=5-1.
故选A.
4.
【答案】
D
【解答】
解:当AD>BD时,
AD=5-12×2=5-1,
BD=2-(5-1)=3-5.
故选D.
5.
【答案】
C
【解答】
解:A、所有的正方形,边长相等,所以对应边成比例,角都是直角,相等,所以都相似,故本选项正确,不符合题意;
B、所有的等边三角形,边长相等,所以对应边成比例,角都是60?,相等,所以都相似,故本选项正确,不符合题意;
C、所有的菱形,边长相等,所以对应边成比例,角不一定对应相等,所以不一定都相似,故本选项错误,符合题意;
D、所有的正六边形,边长相等,所以对应边成比例,角都是120?,相等,所以都相似,故本选项正确,不符合题意.
故选C.
6.
【答案】
C
【解答】
解:由比例的性质,得3b=8a,b=8a3,
aa+b=aa+8a3=a11a3=311,
故选:C.
7.
【答案】
C
【解答】
解:∴ 111213
ABBC=DEEF
∵ AB=4,DE=3,EF=6
BC=8
故答案为:C.
8.
【答案】
B
【解答】
解:A、有一个锐角对应相等的两个直角三角形相似,所以A选项错误;
B、如果两个图形位似,那么对应线段平行或在同一条直线直线上,所以B选项正确;
C、两个矩形不一定相似,所以C选项错误;
D、如果将一个三角形的各边长都扩大原来的二倍,则其面积将扩大4倍,所以D选项错误.
故选B.
9.
【答案】
C
【解答】
解:∵ AD?//?BE?//?CF,
∴ ABBC=DEEF,即510=4EF,
解得,EF=8,
故选:C.
10.
【答案】
D
【解答】
∵ AD?//?BC,
∴ △CBE∽△AED,
∴ BE:AE=CE:ED=3:5,
∵ CD=16.CE+ED=CD,
∴ DE=58×16=10,
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
∠A=∠F
【解答】
解:增加一个条件:∠A=∠F,
∵ AD=BF,
∴ AD+BD=BF+BD
即AB=FD.
在△ABC和△FDE中,
AC=FE,∠A=∠F,AB=FD,(SAS)
∴ △ABC?△FDE.
故答案为:∠A=∠F.
12.
【答案】
2:3
【解答】
解:∵ 三角形的重心到三角形顶点的距离是它到对边中点的距离的2倍
∴ DE:BC=2:(2+1)=2:3.
故答案为:2:3.
13.
【答案】
∠D=∠B或∠E=∠C或ADAB=AEAC
【解答】
∵ ∠1=∠2,
∴ ∠DAE=∠BAC,
∴ 要使△ADE∽△ABC,则添加的一个条件可以是∠D=∠B或∠E=∠C或ADAB=AEAC.
14.
【答案】
12
【解答】
解:∵ G是△ABC的重心,
∴ AG=2DG,AD=3DG;
∵ EF?//?BC,
∴ AFAC=AGAD=2DG3DG=23,
∵ AC=18,
∴ AF=12.
故答案为:12.
15.
【答案】
30?
【解答】
解:∵ △ABC∽△DEF,∴ ∠D=∠A=30?
故应填30?.
16.
【答案】
2(5-1)
【解答】
解:∵ AB=AC,∠A=36?,
∴ ∠ABC=∠C=72?,
又BD平分∠ABC,
∴ ∠ABD=∠DBC=∠A=36?,
∴ BD=AD=BC,
∴ △ABC∽△BCD,
∴ BC:AC=CD:BC,即BC2=CD?AC=(AC-BC)?AC,
∵ AC=4,
∴ BC2=4(4-BC),
BC2+4BC-16=0,
解得BC=2(5-1)cm.
故答案为:2(5-1).
17.
【答案】
50?
【解答】
解:∵ 一个三角形的两个内角分别为60?和70?,
∴ 第三个内角为180?-60?-70?=50?,
∴ 这个三角形的最小的内角的度数为50?,
∵ 两个三角形是相似形,
∴ 另一个三角形的最小内角的度数为50?.
故答案为:50?.
18.
【答案】
1:4
【解答】
解:依题意,△ABC与△DEF位似,且位似比是1:2,故它们的面积之比是1:4.
19.
【答案】
8
【解答】
解:因为在同一时刻同一地点任何物体的高与其影子长的比值相同,
∵ 1米高的直杆,量得其影长为0.5米,
∴ CDDE=10.5,而CD=2,
∴ DE=2×0.51=1,
∴ BE=BD+DE=3+1=4
∴ ABBE=10.5,
∴ AB=4×10.5=8米.
20.
【答案】
5.6
【解答】
解:根据镜面反射的性质可得:ZCED=∠AEB,又∠CDE=∠ABE=90?
所以△ABE-ADE
所以BEDE=ABCD,即8.42.4=AB1.6
解得:AB=5.6米.
故答案为:5.6.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
解:如图,AE⊥BC,点E为正方形桌子的中心,
MN=0.8m,DE=1m,AE=3m,
∵ MN?//?BC,
∴ △AMN∽△ABC,
∴ MNBC=ADAE,即0.8BC=3-13,
∴ BC=1.2(m),
∴ 桌面在地面上的投影(正方形)面积=1.22=1.44(m2).
【解答】
解:如图,AE⊥BC,点E为正方形桌子的中心,
MN=0.8m,DE=1m,AE=3m,
∵ MN?//?BC,
∴ △AMN∽△ABC,
∴ MNBC=ADAE,即0.8BC=3-13,
∴ BC=1.2(m),
∴ 桌面在地面上的投影(正方形)面积=1.22=1.44(m2).
22.
【答案】
解:(1)设点P到AB的距离为xm,
∵ AB?//?CD,
∴ △PAB∽△PCD,
∴ x3=ABCD=25,
解得x=65m.
∴ 点P到AB的距离为65m;
(2)∵ AB?//?CD,PE⊥CD于D交AB于F,
∴ PF⊥AB,
∴ △PAB∽△PCD,
∴ PFPE=ABCD,
∵ EF=1,
∴ PFPF+1=25,
解得:PF=23.
【解答】
解:(1)设点P到AB的距离为xm,
∵ AB?//?CD,
∴ △PAB∽△PCD,
∴ x3=ABCD=25,
解得x=65m.
∴ 点P到AB的距离为65m;
(2)∵ AB?//?CD,PE⊥CD于D交AB于F,
∴ PF⊥AB,
∴ △PAB∽△PCD,
∴ PFPE=ABCD,
∵ EF=1,
∴ PFPF+1=25,
解得:PF=23.
23.
【答案】
解:(1)∵ DE⊥AC,
∴ ∠DFC=∠FCB=90?.
∴ BC?//?DF,
∴ 四边形BCDP是梯形.
在Rt△ABC中,AC2+BC2=AB2,
∴ AC=AB2-BC2=152-92=12.
在△ACD中,∵ DA=DC,DF⊥AC,
∴ CF=AF=6,
∴ y=12(x+9)×6=3x+27(x>0).
(2)∵ BC=9(定值).理由如下:
∴ 要使△PBC的周长最小,只需PB+PC最小.
∵ 点P是线段AC垂直平分线上的点,
∴ PA=PC,
∴ PB+PC=PB+PA,故只要求PB+PA最小.
如图,显然当P与E重合时PB+PA最小,
此时x=DP=DE,PB+PA=AB,
在△DAE和△ABC中,
∵ BC?//?DF,
∴ ∠AEF=∠B,
∵ ∠DFA=∠ACB=90?,
∴ △DAE∽△ACB,
∴ ADDE=ACAB,
即ADx=1215,
在△AFE和△ACB中
∵ ∠FAE=∠CAB,∠AFE=∠ACB=90?,
∴ △AFE∽△ACB,
∴ EFAE=BCAB,
即6AE=1215,
∴ AE=152.
在Rt△ADE和△CAB中
∵ ∠AEF=∠B,
∴ tan∠AEF=tan∠B,
∴ ADAE=ACBC即AD152=129,
∴ AD=10,
∴ x=252.
∴ 当x=252时,△PBC的周长最小,此时y=1292.
【解答】
解:(1)∵ DE⊥AC,
∴ ∠DFC=∠FCB=90?.
∴ BC?//?DF,
∴ 四边形BCDP是梯形.
在Rt△ABC中,AC2+BC2=AB2,
∴ AC=AB2-BC2=152-92=12.
在△ACD中,∵ DA=DC,DF⊥AC,
∴ CF=AF=6,
∴ y=12(x+9)×6=3x+27(x>0).
(2)∵ BC=9(定值).理由如下:
∴ 要使△PBC的周长最小,只需PB+PC最小.
∵ 点P是线段AC垂直平分线上的点,
∴ PA=PC,
∴ PB+PC=PB+PA,故只要求PB+PA最小.
如图,显然当P与E重合时PB+PA最小,
此时x=DP=DE,PB+PA=AB,
在△DAE和△ABC中,
∵ BC?//?DF,
∴ ∠AEF=∠B,
∵ ∠DFA=∠ACB=90?,
∴ △DAE∽△ACB,
∴ ADDE=ACAB,
即ADx=1215,
在△AFE和△ACB中
∵ ∠FAE=∠CAB,∠AFE=∠ACB=90?,
∴ △AFE∽△ACB,
∴ EFAE=BCAB,
即6AE=1215,
∴ AE=152.
在Rt△ADE和△CAB中
∵ ∠AEF=∠B,
∴ tan∠AEF=tan∠B,
∴ ADAE=ACBC即AD152=129,
∴ AD=10,
∴ x=252.
∴ 当x=252时,△PBC的周长最小,此时y=1292.
24.
【答案】
54(8-x);
(2)∵ DE⊥EF,
∴ ∠BEF+∠AED=90?,
∵ ∠AED+∠ADE=90?,
∴ ∠BEF=∠ADE,
∵ EF?//?AC,
∴ ∠BEF=∠BAC,
∵ ∠DAE=∠ABC=90?,
∴ △ADE∽△BAC,
∴ AEBC=ADAB,
即x6=68,
解得:x=92,
∴ EF=54(8-x)=358;
(3)过点G作GH⊥AB于点H,
则四边形ADGH是矩形,
∴ GH=AD=6,
∵ EF⊥EG,
∴ ∠GEH+∠BEF=90?,
∵ ∠GEH+∠EGH=90?,
∴ ∠EGH=∠BEF,
∵ ∠EHG=∠B=90?,
∴ △EGH∽△FBE,
∵ EF?//?AC,
∴ △BEF∽△BAC,
∴ △HGE∽△BAC,
∴ EGAC=GHAB,
∴ EG10=68,
解得:EG=152,
∵ EF⊥EG,EF?//?AC,
∴ EG⊥AC,
∴ △AEH∽△ACB,
∴ AHEH=ABBC=86=43,
若△EFG∽△HEA,
则EFEG=EHAH,
∴ EF152=34,
解得:EF=458;
∴ AE=x=72;
若△EFG∽△HAE,
则EFEG=AHEH=43,
解得:EF=10,
此时x=0,不符合题意,舍去.
∴ 当AE=72时,△EFG与△AHE相似.
【解答】
解:(1)∵ 在矩形ABCD中,AD=6,AB=8,
∴ BC=AD=6,∠B=90?,
∴ AC=AB2+BC2=10,
∵ EF?//?AC,
∴ △BEF∽△BAC,
∴ EFAC=BEAB,
∵ AE=x,
∴ BE=AB-AE=8-x,
∴ EF10=8-x8,
解得:EF=54(8-x);
(2)∵ DE⊥EF,
∴ ∠BEF+∠AED=90?,
∵ ∠AED+∠ADE=90?,
∴ ∠BEF=∠ADE,
∵ EF?//?AC,
∴ ∠BEF=∠BAC,
∵ ∠DAE=∠ABC=90?,
∴ △ADE∽△BAC,
∴ AEBC=ADAB,
即x6=68,
解得:x=92,
∴ EF=54(8-x)=358;
(3)过点G作GH⊥AB于点H,
则四边形ADGH是矩形,
∴ GH=AD=6,
∵ EF⊥EG,
∴ ∠GEH+∠BEF=90?,
∵ ∠GEH+∠EGH=90?,
∴ ∠EGH=∠BEF,
∵ ∠EHG=∠B=90?,
∴ △EGH∽△FBE,
∵ EF?//?AC,
∴ △BEF∽△BAC,
∴ △HGE∽△BAC,
∴ EGAC=GHAB,
∴ EG10=68,
解得:EG=152,
∵ EF⊥EG,EF?//?AC,
∴ EG⊥AC,
∴ △AEH∽△ACB,
∴ AHEH=ABBC=86=43,
若△EFG∽△HEA,
则EFEG=EHAH,
∴ EF152=34,
解得:EF=458;
∴ AE=x=72;
若△EFG∽△HAE,
则EFEG=AHEH=43,
解得:EF=10,
此时x=0,不符合题意,舍去.
∴ 当AE=72时,△EFG与△AHE相似.
25.
【答案】
(1)BE=DG,BE⊥DG;
(2)证明见解析;
(3)4
【解答】
(1)①:四边形ABCD和四边形AEFG是正方形,
..AE=AG,AB=AD,LBAD=LEAG=90?,
∴ _BAE=LDAG,
在△ABE和△ADG中,
AB=AD
\∠B.AE=∠D.AG
AE=AG
..ΔABE=ΔADG(SAS),
∴ BE=DG;
○如图2,延长BE交AD于G,交DG于H,
A_.B
图2
由①知,ΔABE=ΔADG,
∴ .zABE=LADG,
LAGB+LABE=90?,
…._AGB+LADG=90?,
2AGB=LDGH,
..zDGH+LADG=90?,
._DHB=90?,
..BEIDG
(2)四边形ABCD与四边形AEFG都为矩形,
.么BAD=LDAG,
..zBAE=LDAG,
AD=2AB,AG=2AE,
∴ ABAD=AEAG=12
..ΔABE-△ADG,
∴ .zABE=LADG,
LAGB+LABE=90?,
…._AGB+LADG=90?,
LAGB=LDGH,
..zDGH+zADG=90?,
..zDHB=90?,
.BEIDG;
(3)如图4,(为了说明点B,E,F在同一条线上,特意画的图形)
C
:EGIIAB,
..zDME=zDAB=90?,
在RtΔAEG中,AE=1,
..AG=2AE=2,
根据勾股定理得,EG=、5,
:AB=、5,
..EG=AB,
:EGIIAB,
…四边形ABEG是平行四边形,
.AGIIBE,
AGlIEF,
…点B,E,F在同一条直线上如图5,
DC
Fl
c(________E
AB图5
.2AEB=90?,
在Rt△ABE中,根据勾股定理得,BE=AB2-AE==2,
由(3)知,ΔABE-△ADG,
∴ BEDG=ABAD=12
∴ 2DG=12
..DG=4.
(满分120分;时间:90分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
1. 已知四条线段a、b、c、d依次成比例,且a=1,b=3,c=3,则d=( ? ? ??)
A.3 B.6 C.8 D.9
?
2. 如果2a=5b,那么下列比例式中正确的是(? ? ? ? )
A.ab=25 B.a5=2b C.ab=52 D.a2=b5
?
3. 已知点C是线段AB的黄金分割点,且AC>BC,AB=2,则AC为( )
A.5-1 B.3-5 C.5-12 D.0.618
?
4. 点D是线段AB的黄金分割点(AD>BD),若AB=2,则BD=(? ? ? ? )
A.5-12 B.3-52 C.5-1 D.3-5
?
5. 下列结论错误的是( )
A.所有的正方形都相似 B.所有的等边三角形都相似
C.所有的菱形都相似 D.所有的正六边形都相似
?
6. 若ab=38,则aa+b的值是( )
A.811 B.613 C.311 D.35
?
7. 如图L1?//L2?//L3,AB=4,DE=3,EF=6,则BC的长( )
A.4 B.6 C.8 D.10
?
8. 下列语句正确的是( )
A.有一个角对应相等的两个直角三角形相似
B.如果两个图形位似,那么对应线段平行或在同一条直线直线上
C.两个矩形一定相似
D.如果将一个三角形的各边长都扩大二倍,则其面积将扩大4倍
?
9. 如图,AD?//?BE?//?CF,直线m,n与这三条平行线分别交于点A、B、C和点D、E、F,已知AB=5,BC=10,DE=4,则EF的长为( )
A.12.5 B.12 C.8 D.4
?
10. 如图,AB与CD相交于点E,AD?//?BC,BEAE=35,CD=16,则DE的长为( )
A.3 B.6 C.485 D.10
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
11. 如图,点A,D,B,F在一条直线上,AC=EF,AD=FB,要使△ABC?△FDE,需添加的条件是________(填一个即可).
?
12. 如图,点G是△ABC的重心,点D、E分别在边AB、AC上,DE过点G,且DE?//?BC,则DEBC的值为________.
?
13. 如图,△ADE和△ABC中,∠1=∠2,请添加一个适当的条件________,使△ADE∽△ABC(只填一个即可).
?
14. 如图,在△ABC中,AD是中线,G是重心,过点G作EF?//?BC,分别交AB、AC于点E、F,若AC=18,则AF=________.
?
15. 如图,若△ABC∽△DEF,则∠D的度数为________.
?
16. 顶角为36?的等腰三角形被称为黄金三角形,在∠A=36?的△ABC中,AB=AC,BD是∠ABC的角平分线,交AC于D,若AC=4cm,则BC=________cm.
?
17. 已知两个三角形是相似形,其中一个三角形的两个内角分别为60?和70?,那么另一个三角形的最小内角的度数为________.
?
18. 如图,将△DEF缩小为原来的一半,操作方法如下:任意取一点P,连接DP,取DP的中点A,再连接EP,FP,取它们的中点B,C得到△ABC,则△ABC与△DEF的面积之比是________.
?
19. 如图所示,一电线杆AB的影子分别落在了地上和墙上,某一时刻小明竖起1米高的直杆,量得其影长为0.5米,同时,他又量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米,则电线杆AB的高为________米.
?
20. 为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索:根据《科学》中光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子放在离树底(B)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.4米,观察者目高CD=1.6米,则树(AB)的高度约为________米(精确到0.1米).
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
21. 如图,正方形桌子的正上方挂着一盏灯,已知桌面连长为0.8m,桌面的高度为1m,灯泡距地面3m,求桌面在地面上的投影(正方形)面积.
?
22. 电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB?//?CD,AB=2m,CD=5m.
(1)若点P到CD的距离是3m,求点P到AB的距离.
(2)若PE⊥CD于D交AB于F,EF=1m,求PF.
?
23. 如图,四边形ABCD中,AD=CD,∠DAB=∠ACB=90?,过点D作DE⊥AC,垂足为F,DE与AB相交于点E.已知AB=15cm,BC=9cm,P是射线DE上的动点.设DP=xcm(x>0),四边形BCDP的面积为ycm2.
(1)求y关于x的函数关系式;
(2)当x为何值时,△PBC的周长最小,并求出此时y的值.
?
24. 如图(1),在矩形ABCD中,AD=6,AB=8,点E是AB边上-动点(点E不与点A、B重合),过点E作EF?//?AC交BC于点F,连接ED.
(1)设AE=x,则EF=________;
(2)若DE⊥EF,求EF的长;
(3)如图(2),过点E作EG⊥EF.交AC于点H,交直线CD于点G,连接AG、FG,随着点E在线段AB上的运动,当AE为何值时,△EFG与△AHE相似?
?
25. 如图1,正方形ABCD和正方形AEFG,连接DG,BE.
(1)发现:当正方形AEFG绕点A旋转,如图2,①线段DG与BE之间的数量关系是 ?? ;②直线DG与直线BE之间的位置关系是 ?? .
(2)探究:如图3,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE,证明:直线DG⊥BE.
(3)应用:在(2)情况下,连结GE(点E在AB上方),若GE?//?AB,且AB=,AE=1,则线段DG是多少?(直接写出结论)
?
参考答案与试题解析
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
D
【解答】
解:根据题意得:ab=cd,即13=3d,
解得:d=9.
故选D.
2.
【答案】
C
【解答】
解:两边同除以2b得:ab=52,C正确,
其他等式均无法得到.
故选C.
3.
【答案】
A
【解答】
解:∵ 点C是线段AB的黄金分割点,且AC>BC,
∴ AC=5-12AB,
而AB=2,
∴ AC=5-1.
故选A.
4.
【答案】
D
【解答】
解:当AD>BD时,
AD=5-12×2=5-1,
BD=2-(5-1)=3-5.
故选D.
5.
【答案】
C
【解答】
解:A、所有的正方形,边长相等,所以对应边成比例,角都是直角,相等,所以都相似,故本选项正确,不符合题意;
B、所有的等边三角形,边长相等,所以对应边成比例,角都是60?,相等,所以都相似,故本选项正确,不符合题意;
C、所有的菱形,边长相等,所以对应边成比例,角不一定对应相等,所以不一定都相似,故本选项错误,符合题意;
D、所有的正六边形,边长相等,所以对应边成比例,角都是120?,相等,所以都相似,故本选项正确,不符合题意.
故选C.
6.
【答案】
C
【解答】
解:由比例的性质,得3b=8a,b=8a3,
aa+b=aa+8a3=a11a3=311,
故选:C.
7.
【答案】
C
【解答】
解:∴ 111213
ABBC=DEEF
∵ AB=4,DE=3,EF=6
BC=8
故答案为:C.
8.
【答案】
B
【解答】
解:A、有一个锐角对应相等的两个直角三角形相似,所以A选项错误;
B、如果两个图形位似,那么对应线段平行或在同一条直线直线上,所以B选项正确;
C、两个矩形不一定相似,所以C选项错误;
D、如果将一个三角形的各边长都扩大原来的二倍,则其面积将扩大4倍,所以D选项错误.
故选B.
9.
【答案】
C
【解答】
解:∵ AD?//?BE?//?CF,
∴ ABBC=DEEF,即510=4EF,
解得,EF=8,
故选:C.
10.
【答案】
D
【解答】
∵ AD?//?BC,
∴ △CBE∽△AED,
∴ BE:AE=CE:ED=3:5,
∵ CD=16.CE+ED=CD,
∴ DE=58×16=10,
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
∠A=∠F
【解答】
解:增加一个条件:∠A=∠F,
∵ AD=BF,
∴ AD+BD=BF+BD
即AB=FD.
在△ABC和△FDE中,
AC=FE,∠A=∠F,AB=FD,(SAS)
∴ △ABC?△FDE.
故答案为:∠A=∠F.
12.
【答案】
2:3
【解答】
解:∵ 三角形的重心到三角形顶点的距离是它到对边中点的距离的2倍
∴ DE:BC=2:(2+1)=2:3.
故答案为:2:3.
13.
【答案】
∠D=∠B或∠E=∠C或ADAB=AEAC
【解答】
∵ ∠1=∠2,
∴ ∠DAE=∠BAC,
∴ 要使△ADE∽△ABC,则添加的一个条件可以是∠D=∠B或∠E=∠C或ADAB=AEAC.
14.
【答案】
12
【解答】
解:∵ G是△ABC的重心,
∴ AG=2DG,AD=3DG;
∵ EF?//?BC,
∴ AFAC=AGAD=2DG3DG=23,
∵ AC=18,
∴ AF=12.
故答案为:12.
15.
【答案】
30?
【解答】
解:∵ △ABC∽△DEF,∴ ∠D=∠A=30?
故应填30?.
16.
【答案】
2(5-1)
【解答】
解:∵ AB=AC,∠A=36?,
∴ ∠ABC=∠C=72?,
又BD平分∠ABC,
∴ ∠ABD=∠DBC=∠A=36?,
∴ BD=AD=BC,
∴ △ABC∽△BCD,
∴ BC:AC=CD:BC,即BC2=CD?AC=(AC-BC)?AC,
∵ AC=4,
∴ BC2=4(4-BC),
BC2+4BC-16=0,
解得BC=2(5-1)cm.
故答案为:2(5-1).
17.
【答案】
50?
【解答】
解:∵ 一个三角形的两个内角分别为60?和70?,
∴ 第三个内角为180?-60?-70?=50?,
∴ 这个三角形的最小的内角的度数为50?,
∵ 两个三角形是相似形,
∴ 另一个三角形的最小内角的度数为50?.
故答案为:50?.
18.
【答案】
1:4
【解答】
解:依题意,△ABC与△DEF位似,且位似比是1:2,故它们的面积之比是1:4.
19.
【答案】
8
【解答】
解:因为在同一时刻同一地点任何物体的高与其影子长的比值相同,
∵ 1米高的直杆,量得其影长为0.5米,
∴ CDDE=10.5,而CD=2,
∴ DE=2×0.51=1,
∴ BE=BD+DE=3+1=4
∴ ABBE=10.5,
∴ AB=4×10.5=8米.
20.
【答案】
5.6
【解答】
解:根据镜面反射的性质可得:ZCED=∠AEB,又∠CDE=∠ABE=90?
所以△ABE-ADE
所以BEDE=ABCD,即8.42.4=AB1.6
解得:AB=5.6米.
故答案为:5.6.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
解:如图,AE⊥BC,点E为正方形桌子的中心,
MN=0.8m,DE=1m,AE=3m,
∵ MN?//?BC,
∴ △AMN∽△ABC,
∴ MNBC=ADAE,即0.8BC=3-13,
∴ BC=1.2(m),
∴ 桌面在地面上的投影(正方形)面积=1.22=1.44(m2).
【解答】
解:如图,AE⊥BC,点E为正方形桌子的中心,
MN=0.8m,DE=1m,AE=3m,
∵ MN?//?BC,
∴ △AMN∽△ABC,
∴ MNBC=ADAE,即0.8BC=3-13,
∴ BC=1.2(m),
∴ 桌面在地面上的投影(正方形)面积=1.22=1.44(m2).
22.
【答案】
解:(1)设点P到AB的距离为xm,
∵ AB?//?CD,
∴ △PAB∽△PCD,
∴ x3=ABCD=25,
解得x=65m.
∴ 点P到AB的距离为65m;
(2)∵ AB?//?CD,PE⊥CD于D交AB于F,
∴ PF⊥AB,
∴ △PAB∽△PCD,
∴ PFPE=ABCD,
∵ EF=1,
∴ PFPF+1=25,
解得:PF=23.
【解答】
解:(1)设点P到AB的距离为xm,
∵ AB?//?CD,
∴ △PAB∽△PCD,
∴ x3=ABCD=25,
解得x=65m.
∴ 点P到AB的距离为65m;
(2)∵ AB?//?CD,PE⊥CD于D交AB于F,
∴ PF⊥AB,
∴ △PAB∽△PCD,
∴ PFPE=ABCD,
∵ EF=1,
∴ PFPF+1=25,
解得:PF=23.
23.
【答案】
解:(1)∵ DE⊥AC,
∴ ∠DFC=∠FCB=90?.
∴ BC?//?DF,
∴ 四边形BCDP是梯形.
在Rt△ABC中,AC2+BC2=AB2,
∴ AC=AB2-BC2=152-92=12.
在△ACD中,∵ DA=DC,DF⊥AC,
∴ CF=AF=6,
∴ y=12(x+9)×6=3x+27(x>0).
(2)∵ BC=9(定值).理由如下:
∴ 要使△PBC的周长最小,只需PB+PC最小.
∵ 点P是线段AC垂直平分线上的点,
∴ PA=PC,
∴ PB+PC=PB+PA,故只要求PB+PA最小.
如图,显然当P与E重合时PB+PA最小,
此时x=DP=DE,PB+PA=AB,
在△DAE和△ABC中,
∵ BC?//?DF,
∴ ∠AEF=∠B,
∵ ∠DFA=∠ACB=90?,
∴ △DAE∽△ACB,
∴ ADDE=ACAB,
即ADx=1215,
在△AFE和△ACB中
∵ ∠FAE=∠CAB,∠AFE=∠ACB=90?,
∴ △AFE∽△ACB,
∴ EFAE=BCAB,
即6AE=1215,
∴ AE=152.
在Rt△ADE和△CAB中
∵ ∠AEF=∠B,
∴ tan∠AEF=tan∠B,
∴ ADAE=ACBC即AD152=129,
∴ AD=10,
∴ x=252.
∴ 当x=252时,△PBC的周长最小,此时y=1292.
【解答】
解:(1)∵ DE⊥AC,
∴ ∠DFC=∠FCB=90?.
∴ BC?//?DF,
∴ 四边形BCDP是梯形.
在Rt△ABC中,AC2+BC2=AB2,
∴ AC=AB2-BC2=152-92=12.
在△ACD中,∵ DA=DC,DF⊥AC,
∴ CF=AF=6,
∴ y=12(x+9)×6=3x+27(x>0).
(2)∵ BC=9(定值).理由如下:
∴ 要使△PBC的周长最小,只需PB+PC最小.
∵ 点P是线段AC垂直平分线上的点,
∴ PA=PC,
∴ PB+PC=PB+PA,故只要求PB+PA最小.
如图,显然当P与E重合时PB+PA最小,
此时x=DP=DE,PB+PA=AB,
在△DAE和△ABC中,
∵ BC?//?DF,
∴ ∠AEF=∠B,
∵ ∠DFA=∠ACB=90?,
∴ △DAE∽△ACB,
∴ ADDE=ACAB,
即ADx=1215,
在△AFE和△ACB中
∵ ∠FAE=∠CAB,∠AFE=∠ACB=90?,
∴ △AFE∽△ACB,
∴ EFAE=BCAB,
即6AE=1215,
∴ AE=152.
在Rt△ADE和△CAB中
∵ ∠AEF=∠B,
∴ tan∠AEF=tan∠B,
∴ ADAE=ACBC即AD152=129,
∴ AD=10,
∴ x=252.
∴ 当x=252时,△PBC的周长最小,此时y=1292.
24.
【答案】
54(8-x);
(2)∵ DE⊥EF,
∴ ∠BEF+∠AED=90?,
∵ ∠AED+∠ADE=90?,
∴ ∠BEF=∠ADE,
∵ EF?//?AC,
∴ ∠BEF=∠BAC,
∵ ∠DAE=∠ABC=90?,
∴ △ADE∽△BAC,
∴ AEBC=ADAB,
即x6=68,
解得:x=92,
∴ EF=54(8-x)=358;
(3)过点G作GH⊥AB于点H,
则四边形ADGH是矩形,
∴ GH=AD=6,
∵ EF⊥EG,
∴ ∠GEH+∠BEF=90?,
∵ ∠GEH+∠EGH=90?,
∴ ∠EGH=∠BEF,
∵ ∠EHG=∠B=90?,
∴ △EGH∽△FBE,
∵ EF?//?AC,
∴ △BEF∽△BAC,
∴ △HGE∽△BAC,
∴ EGAC=GHAB,
∴ EG10=68,
解得:EG=152,
∵ EF⊥EG,EF?//?AC,
∴ EG⊥AC,
∴ △AEH∽△ACB,
∴ AHEH=ABBC=86=43,
若△EFG∽△HEA,
则EFEG=EHAH,
∴ EF152=34,
解得:EF=458;
∴ AE=x=72;
若△EFG∽△HAE,
则EFEG=AHEH=43,
解得:EF=10,
此时x=0,不符合题意,舍去.
∴ 当AE=72时,△EFG与△AHE相似.
【解答】
解:(1)∵ 在矩形ABCD中,AD=6,AB=8,
∴ BC=AD=6,∠B=90?,
∴ AC=AB2+BC2=10,
∵ EF?//?AC,
∴ △BEF∽△BAC,
∴ EFAC=BEAB,
∵ AE=x,
∴ BE=AB-AE=8-x,
∴ EF10=8-x8,
解得:EF=54(8-x);
(2)∵ DE⊥EF,
∴ ∠BEF+∠AED=90?,
∵ ∠AED+∠ADE=90?,
∴ ∠BEF=∠ADE,
∵ EF?//?AC,
∴ ∠BEF=∠BAC,
∵ ∠DAE=∠ABC=90?,
∴ △ADE∽△BAC,
∴ AEBC=ADAB,
即x6=68,
解得:x=92,
∴ EF=54(8-x)=358;
(3)过点G作GH⊥AB于点H,
则四边形ADGH是矩形,
∴ GH=AD=6,
∵ EF⊥EG,
∴ ∠GEH+∠BEF=90?,
∵ ∠GEH+∠EGH=90?,
∴ ∠EGH=∠BEF,
∵ ∠EHG=∠B=90?,
∴ △EGH∽△FBE,
∵ EF?//?AC,
∴ △BEF∽△BAC,
∴ △HGE∽△BAC,
∴ EGAC=GHAB,
∴ EG10=68,
解得:EG=152,
∵ EF⊥EG,EF?//?AC,
∴ EG⊥AC,
∴ △AEH∽△ACB,
∴ AHEH=ABBC=86=43,
若△EFG∽△HEA,
则EFEG=EHAH,
∴ EF152=34,
解得:EF=458;
∴ AE=x=72;
若△EFG∽△HAE,
则EFEG=AHEH=43,
解得:EF=10,
此时x=0,不符合题意,舍去.
∴ 当AE=72时,△EFG与△AHE相似.
25.
【答案】
(1)BE=DG,BE⊥DG;
(2)证明见解析;
(3)4
【解答】
(1)①:四边形ABCD和四边形AEFG是正方形,
..AE=AG,AB=AD,LBAD=LEAG=90?,
∴ _BAE=LDAG,
在△ABE和△ADG中,
AB=AD
\∠B.AE=∠D.AG
AE=AG
..ΔABE=ΔADG(SAS),
∴ BE=DG;
○如图2,延长BE交AD于G,交DG于H,
A_.B
图2
由①知,ΔABE=ΔADG,
∴ .zABE=LADG,
LAGB+LABE=90?,
…._AGB+LADG=90?,
2AGB=LDGH,
..zDGH+LADG=90?,
._DHB=90?,
..BEIDG
(2)四边形ABCD与四边形AEFG都为矩形,
.么BAD=LDAG,
..zBAE=LDAG,
AD=2AB,AG=2AE,
∴ ABAD=AEAG=12
..ΔABE-△ADG,
∴ .zABE=LADG,
LAGB+LABE=90?,
…._AGB+LADG=90?,
LAGB=LDGH,
..zDGH+zADG=90?,
..zDHB=90?,
.BEIDG;
(3)如图4,(为了说明点B,E,F在同一条线上,特意画的图形)
C
:EGIIAB,
..zDME=zDAB=90?,
在RtΔAEG中,AE=1,
..AG=2AE=2,
根据勾股定理得,EG=、5,
:AB=、5,
..EG=AB,
:EGIIAB,
…四边形ABEG是平行四边形,
.AGIIBE,
AGlIEF,
…点B,E,F在同一条直线上如图5,
DC
Fl
c(________E
AB图5
.2AEB=90?,
在Rt△ABE中,根据勾股定理得,BE=AB2-AE==2,
由(3)知,ΔABE-△ADG,
∴ BEDG=ABAD=12
∴ 2DG=12
..DG=4.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
