2020-2021学年苏科版七年级下册7.1 探索直线平行的条件课件(17张)
文档属性
| 名称 | 2020-2021学年苏科版七年级下册7.1 探索直线平行的条件课件(17张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 00:00:00 | ||
图片预览

文档简介
7.1 探索直线平行的条件
第7章 平面图形的认识(二)
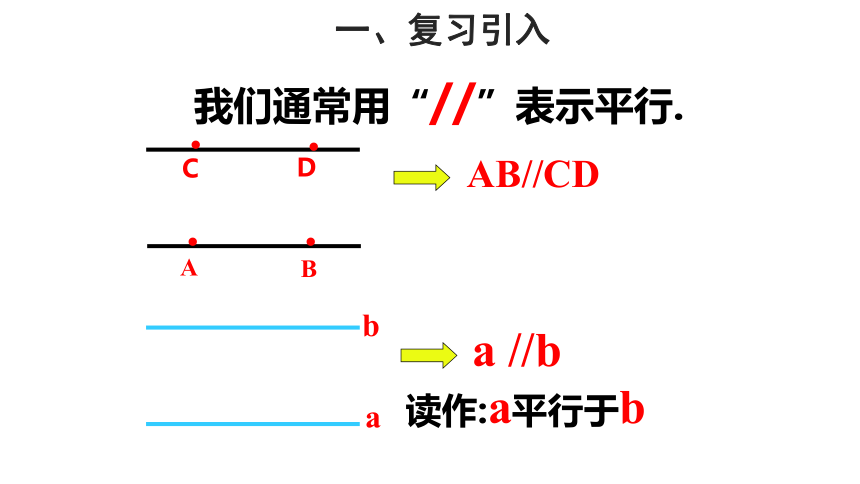
我们通常用“//”表示平行.
C
D
B
A
·
·
AB//CD
a
b
a //b
读作:a平行于b
·
·
一、复习引入
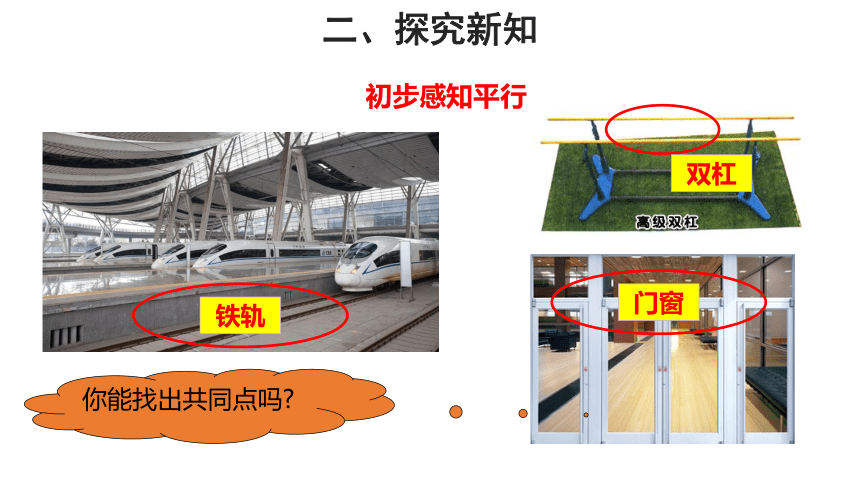
初步感知平行
铁轨
双杠
门窗
你能找出共同点吗?
二、探究新知
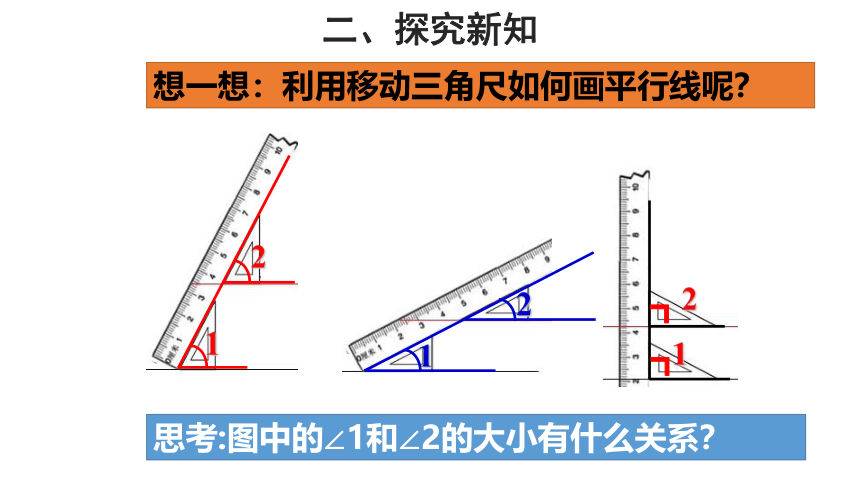
想一想:利用移动三角尺如何画平行线呢?
1
2
1
2
┓
┓
1
2
思考:图中的∠1和∠2的大小有什么关系?
二、探究新知
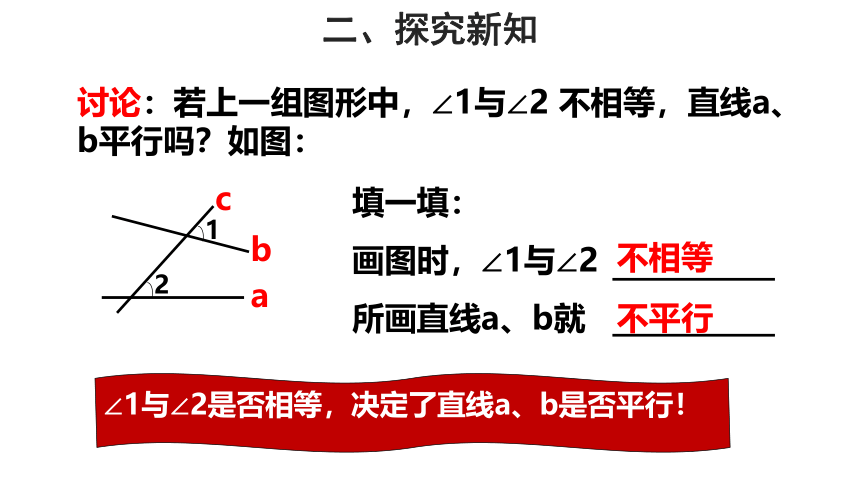
讨论:若上一组图形中,∠1与∠2 不相等,直线a、b平行吗?如图:
a
b
c
1
2
填一填:
画图时,∠1与∠2
所画直线a、b就
不相等
不平行
∠1与∠2是否相等,决定了直线a、b是否平行!
二、探究新知
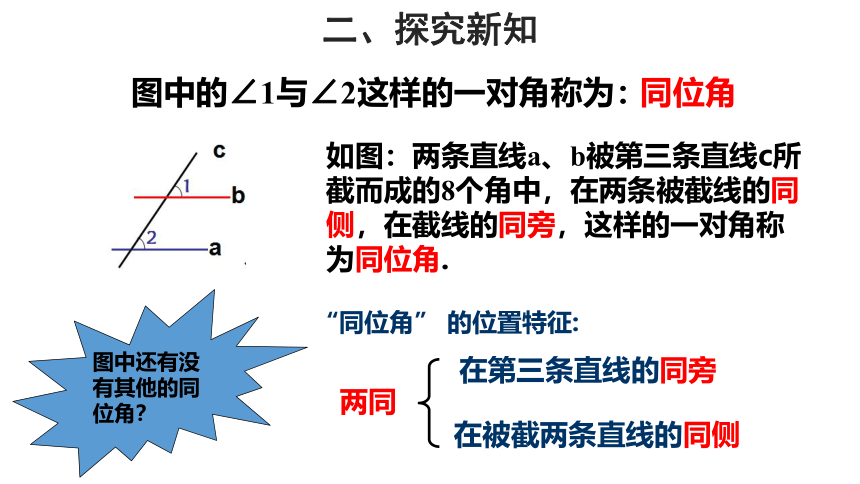
图中的∠1与∠2这样的一对角称为:
同位角
如图:两条直线a、b被第三条直线c所截而成的8个角中,在两条被截线的同侧,在截线的同旁,这样的一对角称为同位角.
“同位角” 的位置特征:
两同
在第三条直线的同旁
在被截两条直线的同侧
图中还有没有其他的同位角?
二、探究新知
F
1
2
3
4
5
6
7
8
D
C
A
B
E
8
4
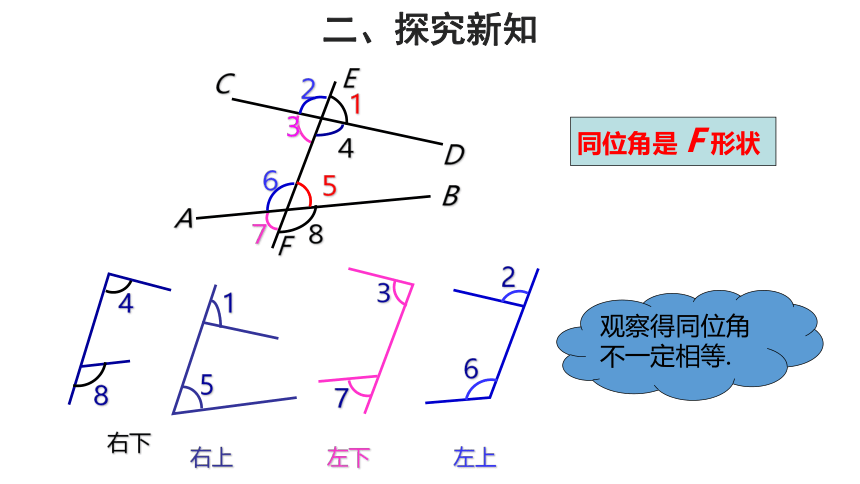
同位角是 F 形状
5
1
6
2
3
7
右上
左上
左下
右下
观察得同位角不一定相等.
二、探究新知
同位角相等,两直线平行.
因为 ∠1 = ∠2 (已知)
所以 a ∥ b (同位角相等,两直线平行)
二、探究新知
(1)木工师傅用角尺在工件上画出两条垂线 a,b, 这两条垂线平行吗?为什么?
(2)由此你能得到什么结论?请与同学交流.
a
b
二、探究新知
探究交流课本中的“议一议”
1、如图1,直线a、b被直线c所截,∠2=∠3,直线a与直线b平行吗?试说明理由.
2、如图2,直线a、b被直线c所截,∠2+∠3=180°,直线a与直线b平行吗?试说明理由.
a
c
1
b
2
3
图1
a
c
1
b
2
3
图2
观察、比较、认识“内错角”、“同旁内角”,探索直线平行的条件.
二、探究新知
如图:在“三线八角”中,
1
3
7
5
2
4
8
6
D
C
A
B
E
F
我们称∠5和∠4为内错角.
两条直线被第三条直线所截而成的8个角中,在两条被截线之间,在截线的两旁,这样的一对角称为内错角.
同位角形如字母“F ”,内错角像个什么呢?
字母 Z
注意:内错角相等,两直线平行.
二、探究新知
如图:在“三线八角”中,
1
3
7
5
2
4
8
6
D
C
A
B
E
F
我们称∠4和∠7为同旁内角.
两条直线a、b被第三条直线c所截而成的8个角中,在两条被截线之间,在截线的同旁,这样的一对角称为同旁内角.
同位角形如字母“F ”,同旁内角像个什么呢?
字母 U
注意:同旁内角互补,两直线平行.
二、探究新知
“三线八角” 小结
两直线被第三条直线所截,构成的八个角中:
①位于两直线同一方、且在第三直线同一侧的两个角,叫做同位角;
②位于两直线之间, 且在第三直线的两侧的两个角,叫做内错角 ;
③ 位于两直线之间, 且在第三直线的 的同旁两个角,叫做同旁内角 .
同位角是 F 形状
内错角是 形状
Z
同旁内角是 形状
U
二、探究新知
两直线平行的判定
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
二、探究新知
如图, ∠1=∠2, ∠B+∠BDE=180°.图中哪些线互相平行,为什么?
B
A
D
E
F
C
1
2
解:(1) AB∥EF.
因为∠1与∠2是AB、EF
被DE截成的内错角,且
∠1=∠2,
所以AB∥EF.
(2) DE∥BC
因为∠B与∠BDE是直线BC、DE
被直线AB所截成的同旁内角,且
∠B+∠BDE=180°,
所以DE∥BC
三、巩固深化
课堂小结:通过本节课的学习,你有什么感悟?
1.知道了同位角、内错角、同旁内角的含义,能识别出同位角、内错角、同旁内角;
2.能利用内错角、同旁内角相等说明两直线平行;
3.通过探索两直线平行条件的活动过程,提高对图形的认识能力和分析能力;
4.学会了一些简单的说理.
四、总结延伸
再 见
第7章 平面图形的认识(二)
我们通常用“//”表示平行.
C
D
B
A
·
·
AB//CD
a
b
a //b
读作:a平行于b
·
·
一、复习引入
初步感知平行
铁轨
双杠
门窗
你能找出共同点吗?
二、探究新知
想一想:利用移动三角尺如何画平行线呢?
1
2
1
2
┓
┓
1
2
思考:图中的∠1和∠2的大小有什么关系?
二、探究新知
讨论:若上一组图形中,∠1与∠2 不相等,直线a、b平行吗?如图:
a
b
c
1
2
填一填:
画图时,∠1与∠2
所画直线a、b就
不相等
不平行
∠1与∠2是否相等,决定了直线a、b是否平行!
二、探究新知
图中的∠1与∠2这样的一对角称为:
同位角
如图:两条直线a、b被第三条直线c所截而成的8个角中,在两条被截线的同侧,在截线的同旁,这样的一对角称为同位角.
“同位角” 的位置特征:
两同
在第三条直线的同旁
在被截两条直线的同侧
图中还有没有其他的同位角?
二、探究新知
F
1
2
3
4
5
6
7
8
D
C
A
B
E
8
4
同位角是 F 形状
5
1
6
2
3
7
右上
左上
左下
右下
观察得同位角不一定相等.
二、探究新知
同位角相等,两直线平行.
因为 ∠1 = ∠2 (已知)
所以 a ∥ b (同位角相等,两直线平行)
二、探究新知
(1)木工师傅用角尺在工件上画出两条垂线 a,b, 这两条垂线平行吗?为什么?
(2)由此你能得到什么结论?请与同学交流.
a
b
二、探究新知
探究交流课本中的“议一议”
1、如图1,直线a、b被直线c所截,∠2=∠3,直线a与直线b平行吗?试说明理由.
2、如图2,直线a、b被直线c所截,∠2+∠3=180°,直线a与直线b平行吗?试说明理由.
a
c
1
b
2
3
图1
a
c
1
b
2
3
图2
观察、比较、认识“内错角”、“同旁内角”,探索直线平行的条件.
二、探究新知
如图:在“三线八角”中,
1
3
7
5
2
4
8
6
D
C
A
B
E
F
我们称∠5和∠4为内错角.
两条直线被第三条直线所截而成的8个角中,在两条被截线之间,在截线的两旁,这样的一对角称为内错角.
同位角形如字母“F ”,内错角像个什么呢?
字母 Z
注意:内错角相等,两直线平行.
二、探究新知
如图:在“三线八角”中,
1
3
7
5
2
4
8
6
D
C
A
B
E
F
我们称∠4和∠7为同旁内角.
两条直线a、b被第三条直线c所截而成的8个角中,在两条被截线之间,在截线的同旁,这样的一对角称为同旁内角.
同位角形如字母“F ”,同旁内角像个什么呢?
字母 U
注意:同旁内角互补,两直线平行.
二、探究新知
“三线八角” 小结
两直线被第三条直线所截,构成的八个角中:
①位于两直线同一方、且在第三直线同一侧的两个角,叫做同位角;
②位于两直线之间, 且在第三直线的两侧的两个角,叫做内错角 ;
③ 位于两直线之间, 且在第三直线的 的同旁两个角,叫做同旁内角 .
同位角是 F 形状
内错角是 形状
Z
同旁内角是 形状
U
二、探究新知
两直线平行的判定
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
二、探究新知
如图, ∠1=∠2, ∠B+∠BDE=180°.图中哪些线互相平行,为什么?
B
A
D
E
F
C
1
2
解:(1) AB∥EF.
因为∠1与∠2是AB、EF
被DE截成的内错角,且
∠1=∠2,
所以AB∥EF.
(2) DE∥BC
因为∠B与∠BDE是直线BC、DE
被直线AB所截成的同旁内角,且
∠B+∠BDE=180°,
所以DE∥BC
三、巩固深化
课堂小结:通过本节课的学习,你有什么感悟?
1.知道了同位角、内错角、同旁内角的含义,能识别出同位角、内错角、同旁内角;
2.能利用内错角、同旁内角相等说明两直线平行;
3.通过探索两直线平行条件的活动过程,提高对图形的认识能力和分析能力;
4.学会了一些简单的说理.
四、总结延伸
再 见
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
