2020-2021学年九年级数学苏教版下册第七章《锐角三角函数》全章综合测试(B卷,有答案)
文档属性
| 名称 | 2020-2021学年九年级数学苏教版下册第七章《锐角三角函数》全章综合测试(B卷,有答案) | 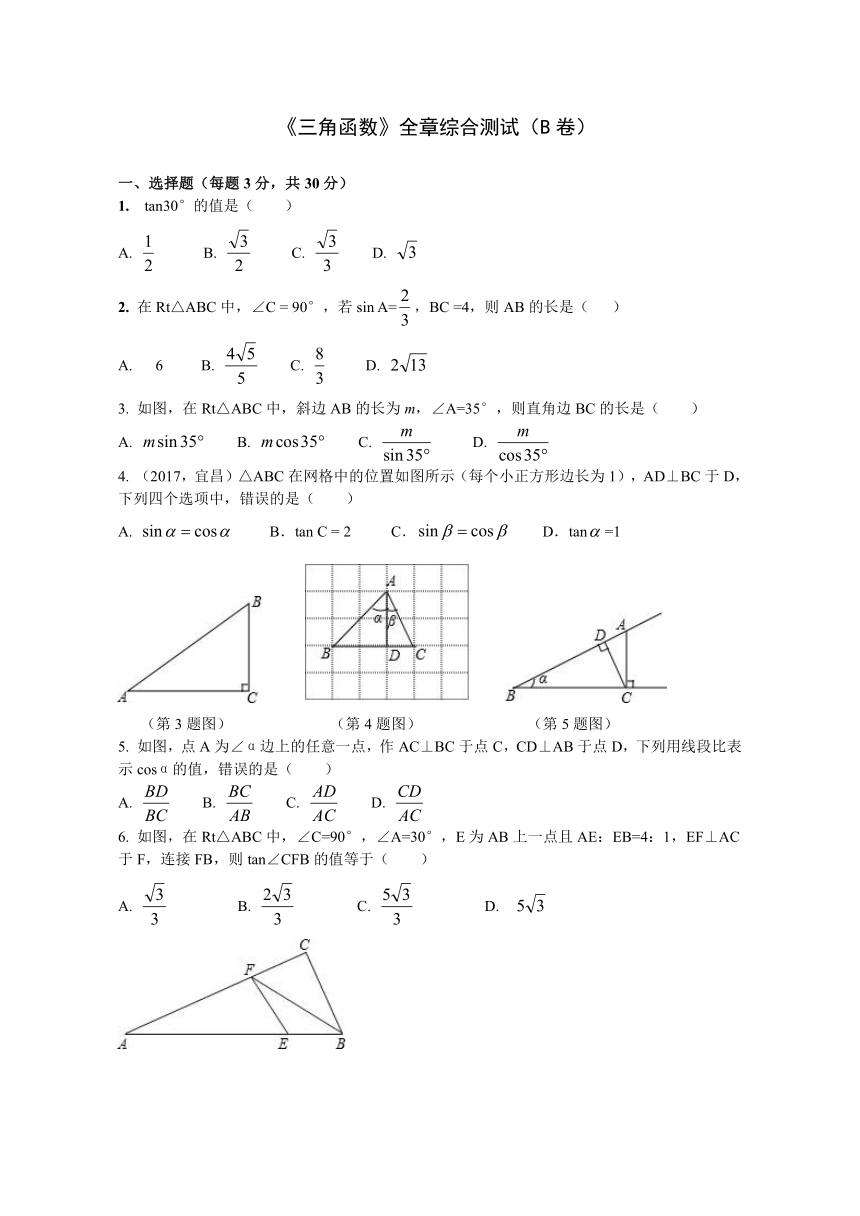 | |
| 格式 | doc | ||
| 文件大小 | 193.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-03 18:17:29 | ||
图片预览


文档简介
《三角函数》全章综合测试(B卷)
一、选择题(每题3分,共30分)
1. tan30°的值是( )
A. B. C. D.
2. 在Rt△ABC中,∠C = 90°,若sin A=,BC =4,则AB的长是( )
A. 6 B. C. D.
3. 如图,在Rt△ABC中,斜边AB的长为m,∠A=35°,则直角边BC的长是( )
A. B. C. D.
4. (2017,宜昌)△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列四个选项中,错误的是( )
A. B.tan C = 2 C. D.tan=1
(第3题图) (第4题图) (第5题图)
5. 如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
A. B. C. D.
6. 如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点且AE:EB=4:1,EF⊥AC于F,连接FB,则tan∠CFB的值等于( )
A. B. C. D.
7. 身高相等的三名同学甲,乙,丙参加风筝比赛,三人放出风筝的线长,线与地面夹角如下表(假设风筝线是拉直的),则三人所放的风筝中( )
同??????学 ????????甲 ????????乙 ????????丙
放出风筝线长 ???????100 m ???????100 m ???????90 m
线与地面交角 ????????40° ????????45° ????????60°
A.甲的最高 B.丙的最高 C.乙的最低 D.丙的最低
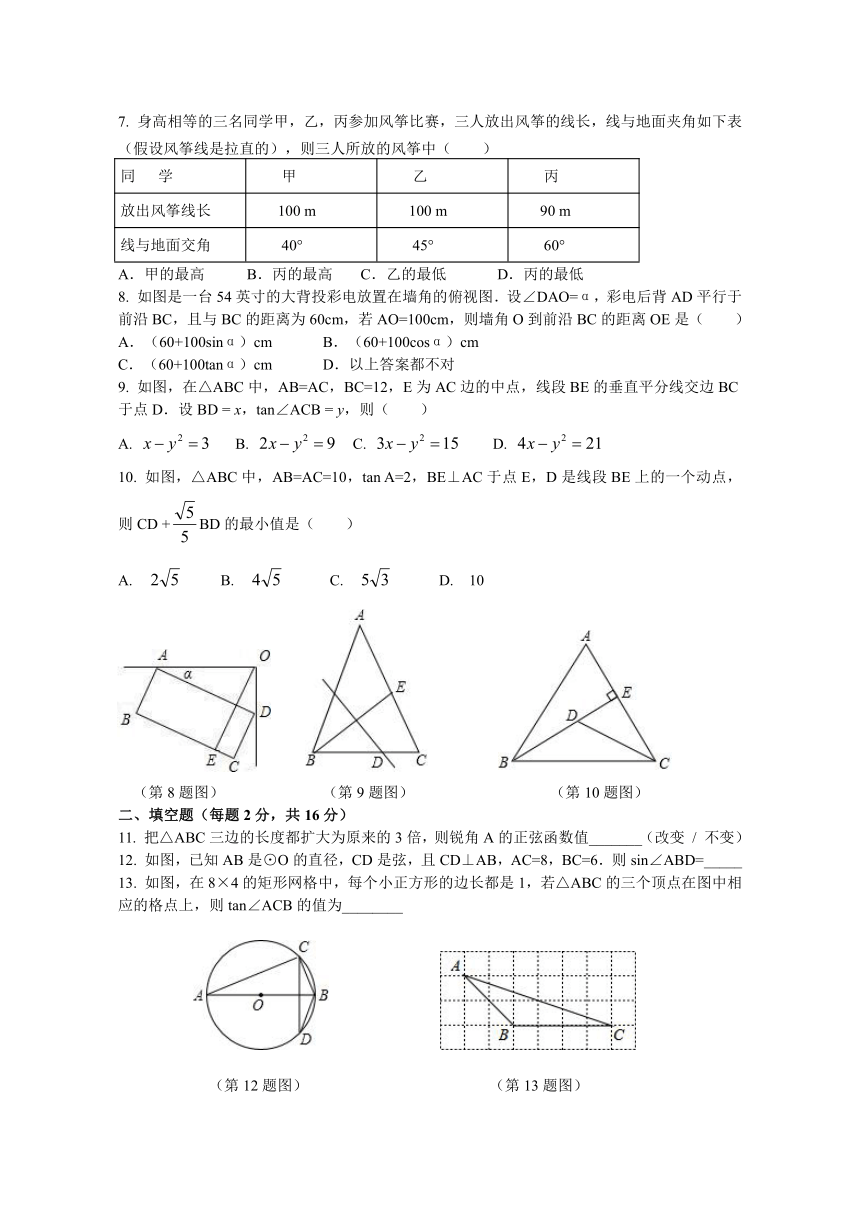
8. 如图是一台54英寸的大背投彩电放置在墙角的俯视图.设∠DAO=α,彩电后背AD平行于前沿BC,且与BC的距离为60cm,若AO=100cm,则墙角O到前沿BC的距离OE是( )
A.(60+100sinα)cm B.(60+100cosα)cm
C.(60+100tanα)cm D.以上答案都不对
9. 如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD = x,tan∠ACB = y,则( )
A. B. C. D.
10. 如图,△ABC中,AB=AC=10,tan A=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD +BD的最小值是( )
A. B. C. D. 10
(第8题图) (第9题图) (第10题图)
二、填空题(每题2分,共16分)
11. 把△ABC三边的长度都扩大为原来的3倍,则锐角A的正弦函数值_______(改变 / 不变)
12. 如图,已知AB是⊙O的直径,CD是弦,且CD⊥AB,AC=8,BC=6.则sin∠ABD=_____
13. 如图,在8×4的矩形网格中,每个小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为________
(第12题图) (第13题图)
14. 在平面直角坐标系中,O是原点,已知点A(2,1)和点B(3,0),则sin∠AOB的值等于________
15. 如图,在△ABC中,AB = AC = 5,BC = 8.若∠BPC =,则tan∠BPC =________
16. 如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=,AB的垂直平分线ED交BC的延长线于D点,垂足为E,则sin∠CAD =________
17. 设∠A为锐角,且sin A = ,则k的取值范围是________
18. 如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB,CD相交于点P,则________,tan∠APD的值等于_________
三、计算题(14分)
19. (1)计算:2 tan60°? tan30°-4cos245°+ sin60°
(2)tan60°-+ 2cos30°+
20. 如图,在△ABC中,tan C =,点D在边BC上,AB = AD,CD = 2BD = 4,求sin B的值.
四、解答题
21. (本题满分6分)如图,小李从西边山脚的点A走了300m后到达山顶C,已知∠A=30°,东边山坡的坡度tan B =.
(1)求山顶C离地面的高度.
(2)求B、C的距离.
22.(本题满分8分)某公司举办热气球表演来庆祝开业,如图,小敏、小亮从A,B两地观测空中C处一个气球,分别测得仰角为37°和45°,A、B两地相距100m.当气球沿与BA平行地飘移100秒后到达D处时,在A处测得气球的仰角为60°.
(1)求气球的高度;
(2)求气球飘移的平均速度.
(参考数据:sin37°= 0.6,cos37°= 0.8,tan37°= 0.75,≈1.7)
23.(本题满分8分)时代购物广场要修建一个地下停车场,停车场的入口设计示意图如图所示,其中斜坡的倾斜角为18°,一楼到地下停车场地面的垂直高度CD=2.8m,一楼到地平线的距离BC = 1m.
(1)为保证斜坡的倾斜角为18°,应在地面上距点B多远的A处开始斜坡的施工?
(结果精确到0.1m)
(2)如果给该购物广场送货的货车高度为2.5m,那么按这样的设计能否保证货车顺利进入地下停车场?并说明理由.(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
24.(本题满分10分)如图,在港口A处的正东方向有两个相距6km的观测点B、C.一艘轮船从A处出发,沿北偏东26°方向航行至D处,在B、C处分别测得∠ABD=45°、∠C=37°.
求轮船航行的距离AD.
(参考数据:sin26°≈0.44,cos26°≈0.90,tan26°≈0.49,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.)
25.(本题满分10分)如图,已知△OAB,点A的坐标为(2,2),点B的坐标为(3,0)
(1)求sin∠AOB的值;
(2)若点P在y轴上,且△POA与△AOB相似,求点P的坐标.
参考答案
1. C 2. A 3.A 4. C 5.C 6. C 7.B 8. A 9. B 10. B
11. 不变 12. 13. 14. 15. 16.
17. 18. 3 2
19.
20.
21. 150m 250m
22. 300m 2.3m/s
23. (1)5.6m (2)能 提示:过点C作CE⊥AD于E,算得CE=2.66 >2.5
24. 20 km 提示:过点D作DH⊥AB,用DH表示BH、CH,根据CH-BH=BC求出DH,
然后在△ADH中,运用三角函数,算出AD的长度。
25. (1)作AD⊥BC,易知∠AOB = 45°,sin∠AOB =
(2) (0,3)或(0,)
提示:分类讨论,题干中已有∠AOB =∠AOP,只需再添加一组“角相等”即可相似。
一、选择题(每题3分,共30分)
1. tan30°的值是( )
A. B. C. D.
2. 在Rt△ABC中,∠C = 90°,若sin A=,BC =4,则AB的长是( )
A. 6 B. C. D.
3. 如图,在Rt△ABC中,斜边AB的长为m,∠A=35°,则直角边BC的长是( )
A. B. C. D.
4. (2017,宜昌)△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列四个选项中,错误的是( )
A. B.tan C = 2 C. D.tan=1
(第3题图) (第4题图) (第5题图)
5. 如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
A. B. C. D.
6. 如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点且AE:EB=4:1,EF⊥AC于F,连接FB,则tan∠CFB的值等于( )
A. B. C. D.
7. 身高相等的三名同学甲,乙,丙参加风筝比赛,三人放出风筝的线长,线与地面夹角如下表(假设风筝线是拉直的),则三人所放的风筝中( )
同??????学 ????????甲 ????????乙 ????????丙
放出风筝线长 ???????100 m ???????100 m ???????90 m
线与地面交角 ????????40° ????????45° ????????60°
A.甲的最高 B.丙的最高 C.乙的最低 D.丙的最低
8. 如图是一台54英寸的大背投彩电放置在墙角的俯视图.设∠DAO=α,彩电后背AD平行于前沿BC,且与BC的距离为60cm,若AO=100cm,则墙角O到前沿BC的距离OE是( )
A.(60+100sinα)cm B.(60+100cosα)cm
C.(60+100tanα)cm D.以上答案都不对
9. 如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD = x,tan∠ACB = y,则( )
A. B. C. D.
10. 如图,△ABC中,AB=AC=10,tan A=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD +BD的最小值是( )
A. B. C. D. 10
(第8题图) (第9题图) (第10题图)
二、填空题(每题2分,共16分)
11. 把△ABC三边的长度都扩大为原来的3倍,则锐角A的正弦函数值_______(改变 / 不变)
12. 如图,已知AB是⊙O的直径,CD是弦,且CD⊥AB,AC=8,BC=6.则sin∠ABD=_____
13. 如图,在8×4的矩形网格中,每个小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为________
(第12题图) (第13题图)
14. 在平面直角坐标系中,O是原点,已知点A(2,1)和点B(3,0),则sin∠AOB的值等于________
15. 如图,在△ABC中,AB = AC = 5,BC = 8.若∠BPC =,则tan∠BPC =________
16. 如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=,AB的垂直平分线ED交BC的延长线于D点,垂足为E,则sin∠CAD =________
17. 设∠A为锐角,且sin A = ,则k的取值范围是________
18. 如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB,CD相交于点P,则________,tan∠APD的值等于_________
三、计算题(14分)
19. (1)计算:2 tan60°? tan30°-4cos245°+ sin60°
(2)tan60°-+ 2cos30°+
20. 如图,在△ABC中,tan C =,点D在边BC上,AB = AD,CD = 2BD = 4,求sin B的值.
四、解答题
21. (本题满分6分)如图,小李从西边山脚的点A走了300m后到达山顶C,已知∠A=30°,东边山坡的坡度tan B =.
(1)求山顶C离地面的高度.
(2)求B、C的距离.
22.(本题满分8分)某公司举办热气球表演来庆祝开业,如图,小敏、小亮从A,B两地观测空中C处一个气球,分别测得仰角为37°和45°,A、B两地相距100m.当气球沿与BA平行地飘移100秒后到达D处时,在A处测得气球的仰角为60°.
(1)求气球的高度;
(2)求气球飘移的平均速度.
(参考数据:sin37°= 0.6,cos37°= 0.8,tan37°= 0.75,≈1.7)
23.(本题满分8分)时代购物广场要修建一个地下停车场,停车场的入口设计示意图如图所示,其中斜坡的倾斜角为18°,一楼到地下停车场地面的垂直高度CD=2.8m,一楼到地平线的距离BC = 1m.
(1)为保证斜坡的倾斜角为18°,应在地面上距点B多远的A处开始斜坡的施工?
(结果精确到0.1m)
(2)如果给该购物广场送货的货车高度为2.5m,那么按这样的设计能否保证货车顺利进入地下停车场?并说明理由.(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
24.(本题满分10分)如图,在港口A处的正东方向有两个相距6km的观测点B、C.一艘轮船从A处出发,沿北偏东26°方向航行至D处,在B、C处分别测得∠ABD=45°、∠C=37°.
求轮船航行的距离AD.
(参考数据:sin26°≈0.44,cos26°≈0.90,tan26°≈0.49,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.)
25.(本题满分10分)如图,已知△OAB,点A的坐标为(2,2),点B的坐标为(3,0)
(1)求sin∠AOB的值;
(2)若点P在y轴上,且△POA与△AOB相似,求点P的坐标.
参考答案
1. C 2. A 3.A 4. C 5.C 6. C 7.B 8. A 9. B 10. B
11. 不变 12. 13. 14. 15. 16.
17. 18. 3 2
19.
20.
21. 150m 250m
22. 300m 2.3m/s
23. (1)5.6m (2)能 提示:过点C作CE⊥AD于E,算得CE=2.66 >2.5
24. 20 km 提示:过点D作DH⊥AB,用DH表示BH、CH,根据CH-BH=BC求出DH,
然后在△ADH中,运用三角函数,算出AD的长度。
25. (1)作AD⊥BC,易知∠AOB = 45°,sin∠AOB =
(2) (0,3)或(0,)
提示:分类讨论,题干中已有∠AOB =∠AOP,只需再添加一组“角相等”即可相似。
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
