2020-2021学年人教版七年级下册数学 5.3.1平行线的性质 同步测试(word版含答案)
文档属性
| 名称 | 2020-2021学年人教版七年级下册数学 5.3.1平行线的性质 同步测试(word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 127.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 18:13:15 | ||
图片预览



文档简介
5.3.1平行线的性质 同步测试
一.选择题
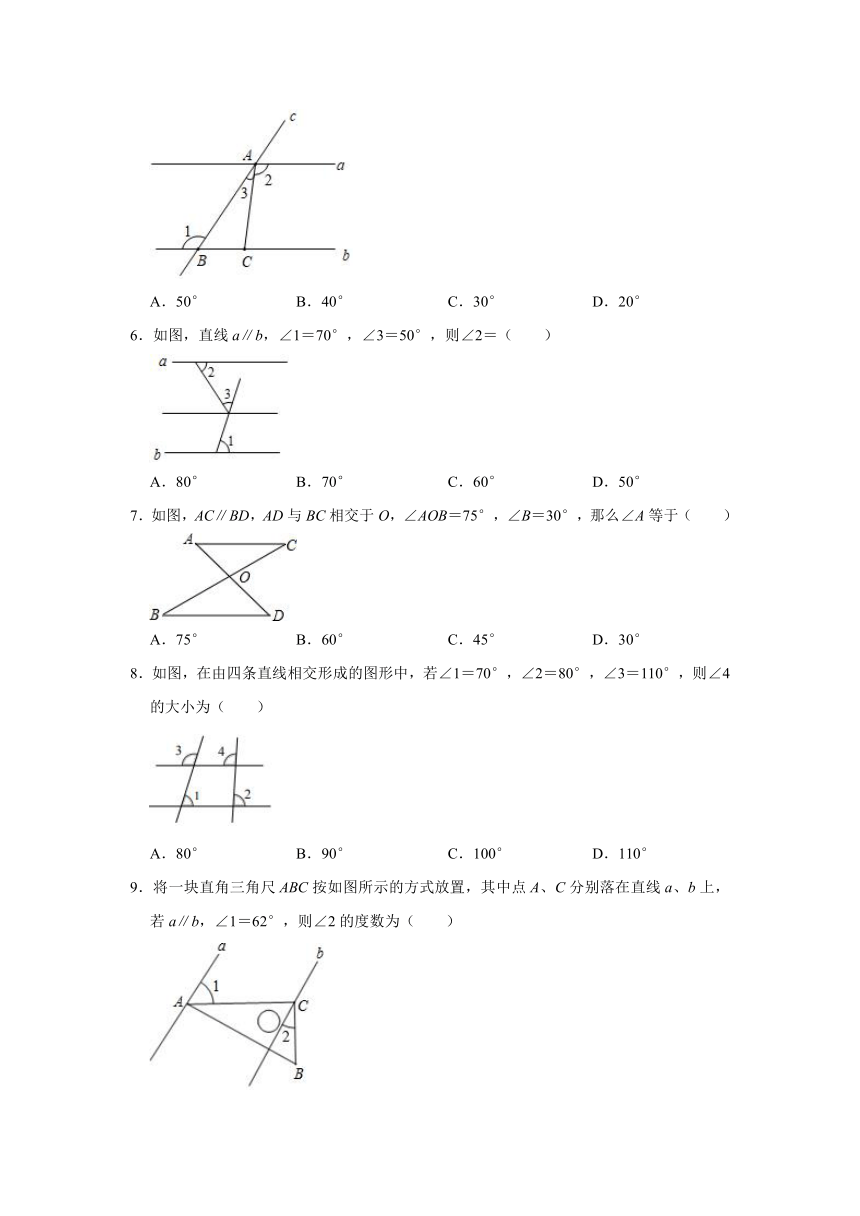
1.如图,两平行线AB,CD被CE所截,∠1=70°,则∠2的度数是( )
A.100° B.110° C.120° D.130°
2.如图,AB∥CD,若∠2=134°,则∠1等于( )
A.36° B.46° C.50° D.55°
3.如图,三角板的直角顶点落在矩形纸片的一边上.若∠1=40°,则∠2=( )
A.35° B.40° C.45° D.50°
4.如图2,将三角板的直角顶点C在直尺的一边上,∠ACB=90°,∠2=56°,则∠1的度数等于( )
A.54° B.44° C.24° D.34°
5.如图,已知直线a∥b,直线c分别交直线a,b于点A,B,在直线b上取点C,连接AC.若∠1=130°,∠2=100°,则∠3的度数为( )
A.50° B.40° C.30° D.20°
6.如图,直线a∥b,∠1=70°,∠3=50°,则∠2=( )
A.80° B.70° C.60° D.50°
7.如图,AC∥BD,AD与BC相交于O,∠AOB=75°,∠B=30°,那么∠A等于( )
A.75° B.60° C.45° D.30°
8.如图,在由四条直线相交形成的图形中,若∠1=70°,∠2=80°,∠3=110°,则∠4的大小为( )
A.80° B.90° C.100° D.110°
9.将一块直角三角尺ABC按如图所示的方式放置,其中点A、C分别落在直线a、b上,若a∥b,∠1=62°,则∠2的度数为( )
A.28° B.30° C.38° D.62°
10.如图,已知AB∥CD,∠1=113°,∠2=63°,则∠C的度数是( )
A.40° B.45° C.50° D.60°
二.填空题
11.如图,已知AB∥CE,∠B=50°,CE平分∠ACD,则∠ACD= °
12.如图,∠1=35°,∠2=35°,∠3=56°23′,则∠4的大小为 .
13.如图,AB∥CD,点M为CD上一点,MF平分∠CME.若∠1=57°,则∠EMD的大小为 度.
14.如图,已知AB∥CD,AD平分∠BAC,∠1=70°,则∠ADC的度数是 .
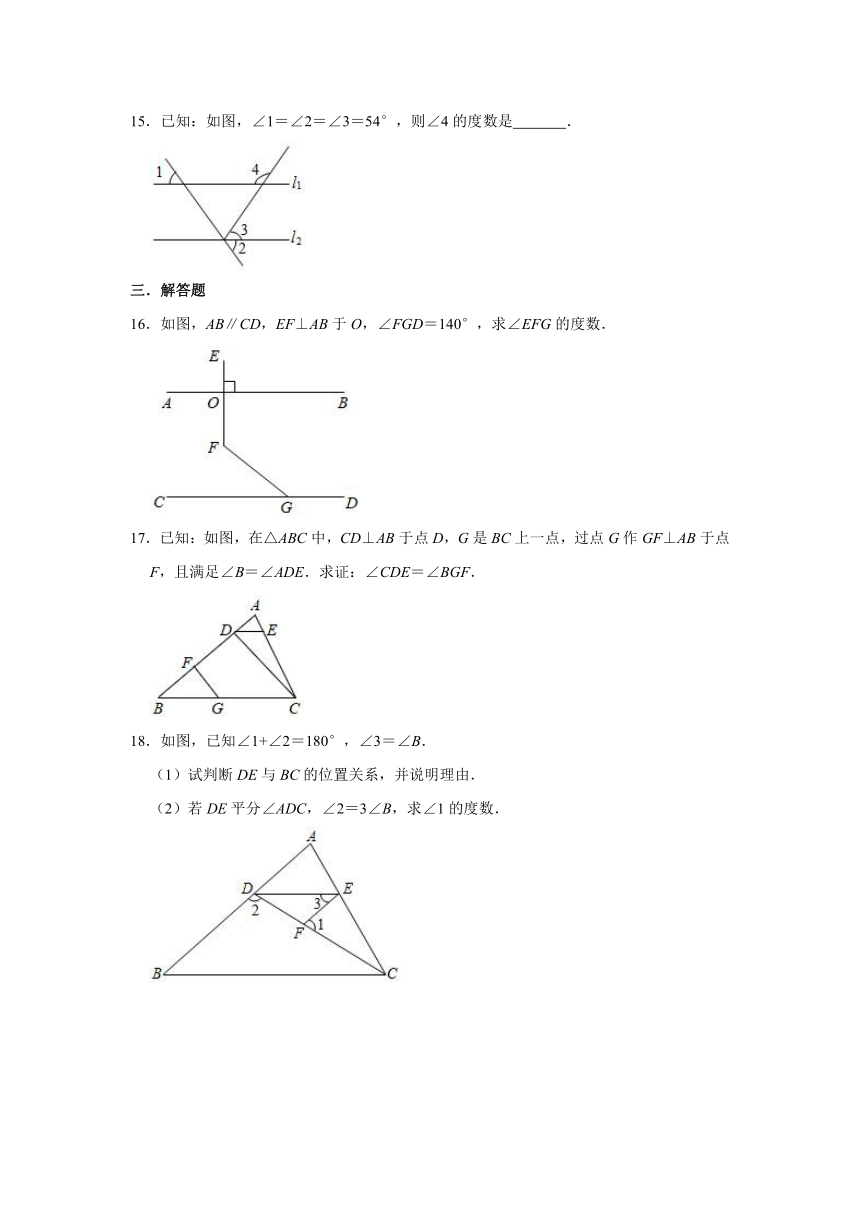
15.已知:如图,∠1=∠2=∠3=54°,则∠4的度数是 .
三.解答题
16.如图,AB∥CD,EF⊥AB于O,∠FGD=140°,求∠EFG的度数.
17.已知:如图,在△ABC中,CD⊥AB于点D,G是BC上一点,过点G作GF⊥AB于点F,且满足∠B=∠ADE.求证:∠CDE=∠BGF.
18.如图,已知∠1+∠2=180°,∠3=∠B.
(1)试判断DE与BC的位置关系,并说明理由.
(2)若DE平分∠ADC,∠2=3∠B,求∠1的度数.
参考答案
一.选择题
1.解:∵两平行线AB,CD被CE所截,
∴∠1+∠BEC=180°,
∵∠1=70°,
∴∠BEC=180°﹣∠1=180°﹣70°=110°,
∵∠2=∠BEC,
∴∠2=110°,
故选:B.
2.解:∵AB∥CD,
∴∠2=∠3,
∵∠2=134°,
∴∠3=134°,
∵∠3+∠1=180°,
∴∠1=46°,
故选:B.
3.解:如图,由题意知:AB∥CD,∠FEG=90°,
∴∠2=∠3,
∵∠1+∠3+90°=180°,
∴∠1+∠2=90°,
∵∠1=40°,
∴∠2=50°.
故选:D.
4.解:如图,
,
∵两条平行线被第三条直线所截,同位角相等,
∴∠3=∠2=56°,
又∵∠1+∠3=∠ACB=90°,
∴∠1=90°﹣56°=34°,
即∠1的度数等于34°.
故选:D.
5.解:∵a∥b,
∴∠1=∠2+∠3,
∵∠1=130°,∠2=100°,
∴∠3=∠1﹣∠2=130°﹣100°=30°,
故选:C.
6.解:如右图所示,
∵a∥b,
∴∠1=∠4,
∴∠1=70°,
∴∠4=70°,
∵∠3=50°,∠2+∠3+∠4=180°,
∴∠2=180°﹣∠3﹣∠4=180°﹣50°﹣70°=60°,
故选:C.
7.解:∵∠AOB=75°,∠B=30°,
∴∠D=∠AOB﹣∠B=45°,
∵AC∥BD,
∴∠A=∠D=45°,
故选:C.
8.解:如图,
∵∠1=70°,
∴∠5=180°﹣70°=110°,
∴∠5=∠3=110°,
∴a∥b,
∴∠2+∠6=180°,
∵∠2=80°,
∴∠6=100°,
∴∠4=∠6=100°.
故选:C.
9.解:如图,
∵a∥b,
∴∠1=∠3=62°,
∵∠2+∠3=90°,
∴∠2=90°﹣∠3=90°﹣62°=28°,
故选:A.
10.解:∵AB∥CD,
∴∠1=∠FGD=113°,
∴∠C=∠FGD﹣∠2=113°﹣63°=50°,
故选:C.
二.填空题
11.解:∵AB∥CE,∠B=50°,
∴∠ECD=∠B=50°,
∵CE平分∠ACD,
∴∠ACD=2∠ECD=2×50°=100°,
故答案为:100.
12.解:如图,
∵∠1=35°,∠2=35°,
∴∠1=∠2,
∴a∥b,
∴∠4=∠5,
∵∠3=56°23′,
∴∠5=180°﹣∠3=123°37′,
∴∠4=123°37′.
故答案为:123°37′.
13.解:∵AB∥CD,
∴∠CMF=∠1=57°,
∵MF平分∠CME,
∴∠CME=2∠CMF=114°.
又∵∠CME+∠EMD=180°,
∴∠EMD=180°﹣∠CME=180°﹣114°=66°.
故答案为:66.
14.解:∵AB∥CD,
∴∠1+∠BAC=180°,
∴∠BAC=180°﹣∠1=180°﹣70°=110°.
∵AD平分∠BAC,
∴∠BAD=∠BAC=×110°=55°.
∵AB∥CD,
∴∠ADC=∠BAD=55°.
故答案为:55°.
15.解:∵∠1=∠2=∠3=54°,
∵∠1=∠5,
∴∠5=∠2,
∴l1∥l2,
∴∠6=∠3,
∴∠4=180°﹣∠6=180°﹣54°=126°,
故答案为:126°.
三.解答题
16.解:过点F作FM∥AB,如图所示.
∵AB∥CD,FM∥AB,
∴FM∥CD,
∴∠MFG=180°﹣∠FGD=180°﹣140°=40°.
∵EF⊥AB,
∴∠BOF=90°,
又∵FM∥AB,
∴∠OFM=180°﹣∠BOF=180°﹣90°=90°,
∴∠EFG=∠OFM+∠MFG=90°+40°=130°.
17.证明:∵CD⊥AB,GF⊥AB,
∴FG∥CD,
∴∠FGB=∠DCB,
∵∠B=∠ADE,
∴DE∥BC,
∴∠EDC=∠DCG,
∴∠CDE=∠BGF.
18.解:(1)DE∥BC,理由如下:
∵∠1+∠4=180°,∠1+∠2=180°,
∴∠2=∠4,
∴AB∥EF,
∴∠3=∠5,
∵∠3=∠B,
∴∠5=∠B,
∴DE∥BC,
(2)∵DE平分∠ADC,
∴∠5=∠6,
∵DE∥BC,
∴∠5=∠B,
∵∠2=3∠B,
∴∠2+∠5+∠6=3∠B+∠B+∠B=180°,
∴∠B=36°,
∴∠2=108°,
∵∠1+∠2=180°,
∴∠1=72°.
一.选择题
1.如图,两平行线AB,CD被CE所截,∠1=70°,则∠2的度数是( )
A.100° B.110° C.120° D.130°
2.如图,AB∥CD,若∠2=134°,则∠1等于( )
A.36° B.46° C.50° D.55°
3.如图,三角板的直角顶点落在矩形纸片的一边上.若∠1=40°,则∠2=( )
A.35° B.40° C.45° D.50°
4.如图2,将三角板的直角顶点C在直尺的一边上,∠ACB=90°,∠2=56°,则∠1的度数等于( )
A.54° B.44° C.24° D.34°
5.如图,已知直线a∥b,直线c分别交直线a,b于点A,B,在直线b上取点C,连接AC.若∠1=130°,∠2=100°,则∠3的度数为( )
A.50° B.40° C.30° D.20°
6.如图,直线a∥b,∠1=70°,∠3=50°,则∠2=( )
A.80° B.70° C.60° D.50°
7.如图,AC∥BD,AD与BC相交于O,∠AOB=75°,∠B=30°,那么∠A等于( )
A.75° B.60° C.45° D.30°
8.如图,在由四条直线相交形成的图形中,若∠1=70°,∠2=80°,∠3=110°,则∠4的大小为( )
A.80° B.90° C.100° D.110°
9.将一块直角三角尺ABC按如图所示的方式放置,其中点A、C分别落在直线a、b上,若a∥b,∠1=62°,则∠2的度数为( )
A.28° B.30° C.38° D.62°
10.如图,已知AB∥CD,∠1=113°,∠2=63°,则∠C的度数是( )
A.40° B.45° C.50° D.60°
二.填空题
11.如图,已知AB∥CE,∠B=50°,CE平分∠ACD,则∠ACD= °
12.如图,∠1=35°,∠2=35°,∠3=56°23′,则∠4的大小为 .
13.如图,AB∥CD,点M为CD上一点,MF平分∠CME.若∠1=57°,则∠EMD的大小为 度.
14.如图,已知AB∥CD,AD平分∠BAC,∠1=70°,则∠ADC的度数是 .
15.已知:如图,∠1=∠2=∠3=54°,则∠4的度数是 .
三.解答题
16.如图,AB∥CD,EF⊥AB于O,∠FGD=140°,求∠EFG的度数.
17.已知:如图,在△ABC中,CD⊥AB于点D,G是BC上一点,过点G作GF⊥AB于点F,且满足∠B=∠ADE.求证:∠CDE=∠BGF.
18.如图,已知∠1+∠2=180°,∠3=∠B.
(1)试判断DE与BC的位置关系,并说明理由.
(2)若DE平分∠ADC,∠2=3∠B,求∠1的度数.
参考答案
一.选择题
1.解:∵两平行线AB,CD被CE所截,
∴∠1+∠BEC=180°,
∵∠1=70°,
∴∠BEC=180°﹣∠1=180°﹣70°=110°,
∵∠2=∠BEC,
∴∠2=110°,
故选:B.
2.解:∵AB∥CD,
∴∠2=∠3,
∵∠2=134°,
∴∠3=134°,
∵∠3+∠1=180°,
∴∠1=46°,
故选:B.
3.解:如图,由题意知:AB∥CD,∠FEG=90°,
∴∠2=∠3,
∵∠1+∠3+90°=180°,
∴∠1+∠2=90°,
∵∠1=40°,
∴∠2=50°.
故选:D.
4.解:如图,
,
∵两条平行线被第三条直线所截,同位角相等,
∴∠3=∠2=56°,
又∵∠1+∠3=∠ACB=90°,
∴∠1=90°﹣56°=34°,
即∠1的度数等于34°.
故选:D.
5.解:∵a∥b,
∴∠1=∠2+∠3,
∵∠1=130°,∠2=100°,
∴∠3=∠1﹣∠2=130°﹣100°=30°,
故选:C.
6.解:如右图所示,
∵a∥b,
∴∠1=∠4,
∴∠1=70°,
∴∠4=70°,
∵∠3=50°,∠2+∠3+∠4=180°,
∴∠2=180°﹣∠3﹣∠4=180°﹣50°﹣70°=60°,
故选:C.
7.解:∵∠AOB=75°,∠B=30°,
∴∠D=∠AOB﹣∠B=45°,
∵AC∥BD,
∴∠A=∠D=45°,
故选:C.
8.解:如图,
∵∠1=70°,
∴∠5=180°﹣70°=110°,
∴∠5=∠3=110°,
∴a∥b,
∴∠2+∠6=180°,
∵∠2=80°,
∴∠6=100°,
∴∠4=∠6=100°.
故选:C.
9.解:如图,
∵a∥b,
∴∠1=∠3=62°,
∵∠2+∠3=90°,
∴∠2=90°﹣∠3=90°﹣62°=28°,
故选:A.
10.解:∵AB∥CD,
∴∠1=∠FGD=113°,
∴∠C=∠FGD﹣∠2=113°﹣63°=50°,
故选:C.
二.填空题
11.解:∵AB∥CE,∠B=50°,
∴∠ECD=∠B=50°,
∵CE平分∠ACD,
∴∠ACD=2∠ECD=2×50°=100°,
故答案为:100.
12.解:如图,
∵∠1=35°,∠2=35°,
∴∠1=∠2,
∴a∥b,
∴∠4=∠5,
∵∠3=56°23′,
∴∠5=180°﹣∠3=123°37′,
∴∠4=123°37′.
故答案为:123°37′.
13.解:∵AB∥CD,
∴∠CMF=∠1=57°,
∵MF平分∠CME,
∴∠CME=2∠CMF=114°.
又∵∠CME+∠EMD=180°,
∴∠EMD=180°﹣∠CME=180°﹣114°=66°.
故答案为:66.
14.解:∵AB∥CD,
∴∠1+∠BAC=180°,
∴∠BAC=180°﹣∠1=180°﹣70°=110°.
∵AD平分∠BAC,
∴∠BAD=∠BAC=×110°=55°.
∵AB∥CD,
∴∠ADC=∠BAD=55°.
故答案为:55°.
15.解:∵∠1=∠2=∠3=54°,
∵∠1=∠5,
∴∠5=∠2,
∴l1∥l2,
∴∠6=∠3,
∴∠4=180°﹣∠6=180°﹣54°=126°,
故答案为:126°.
三.解答题
16.解:过点F作FM∥AB,如图所示.
∵AB∥CD,FM∥AB,
∴FM∥CD,
∴∠MFG=180°﹣∠FGD=180°﹣140°=40°.
∵EF⊥AB,
∴∠BOF=90°,
又∵FM∥AB,
∴∠OFM=180°﹣∠BOF=180°﹣90°=90°,
∴∠EFG=∠OFM+∠MFG=90°+40°=130°.
17.证明:∵CD⊥AB,GF⊥AB,
∴FG∥CD,
∴∠FGB=∠DCB,
∵∠B=∠ADE,
∴DE∥BC,
∴∠EDC=∠DCG,
∴∠CDE=∠BGF.
18.解:(1)DE∥BC,理由如下:
∵∠1+∠4=180°,∠1+∠2=180°,
∴∠2=∠4,
∴AB∥EF,
∴∠3=∠5,
∵∠3=∠B,
∴∠5=∠B,
∴DE∥BC,
(2)∵DE平分∠ADC,
∴∠5=∠6,
∵DE∥BC,
∴∠5=∠B,
∵∠2=3∠B,
∴∠2+∠5+∠6=3∠B+∠B+∠B=180°,
∴∠B=36°,
∴∠2=108°,
∵∠1+∠2=180°,
∴∠1=72°.
