1.3线段的垂直平分线(第2课时)(有答案)
文档属性
| 名称 | 1.3线段的垂直平分线(第2课时)(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 482.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 18:24:33 | ||
图片预览



文档简介
21世纪教育网
–全国领先的中小学教育资源及组卷应用平台
北师大版八年级数学下册第1章三角形的证明
1.3
线段的垂直平分线
第2课时
线段的垂直平分线2
【知识清单】
1、三角形三边垂直平分线性质:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.当三角形是锐角三角形时,交点在其内部;当三角形
是钝角三角形时,交点在其外部;当三角形是直角三角形时,交点
在其斜边的中点上.
2、线段的垂直平分线的作法及其作用.
(1)线段的垂直平分线的作法:
已知:线段AB(如图1所示),求作线段AB的垂直平分线.
作法:①分别以点A和B为圆心,以大于的长为半径作弧,
两弧交于点C和D;
②作直线CD.直线CD就是线段AB的垂直平分线(直线CD与AB的交点就是线段AB的中点).
(2)这个基本作图的另一个作用就是找已知线段的中点.
【经典例题】
例题1、如图所示,A、B、C三点表示三个村庄的地理位置.为了解决吃水难的问题,自来水公司决定在三个村建厂,要求自来水厂到三个村的距离相等.请你设计出自来水厂O点的位置,并说明理由.
【考点】线段垂直平分线的作法和应用.
【分析】根据垂直平分线的性质,作出AB,BC的垂直平分线,两条直线相交于点O,点O位置即可确定.
【解答】连接AB、AC、BC,
作AB、BC的垂直平分线,两线交于点O,
点O就是自来水厂的位置.
根据线段垂直平分线上的点到线段两端点的距离相等可得OA=OB=OC.
【点评】此题主要考查了应用与设计作图,根据垂直平分线的性质得出O点位置是解题关键.
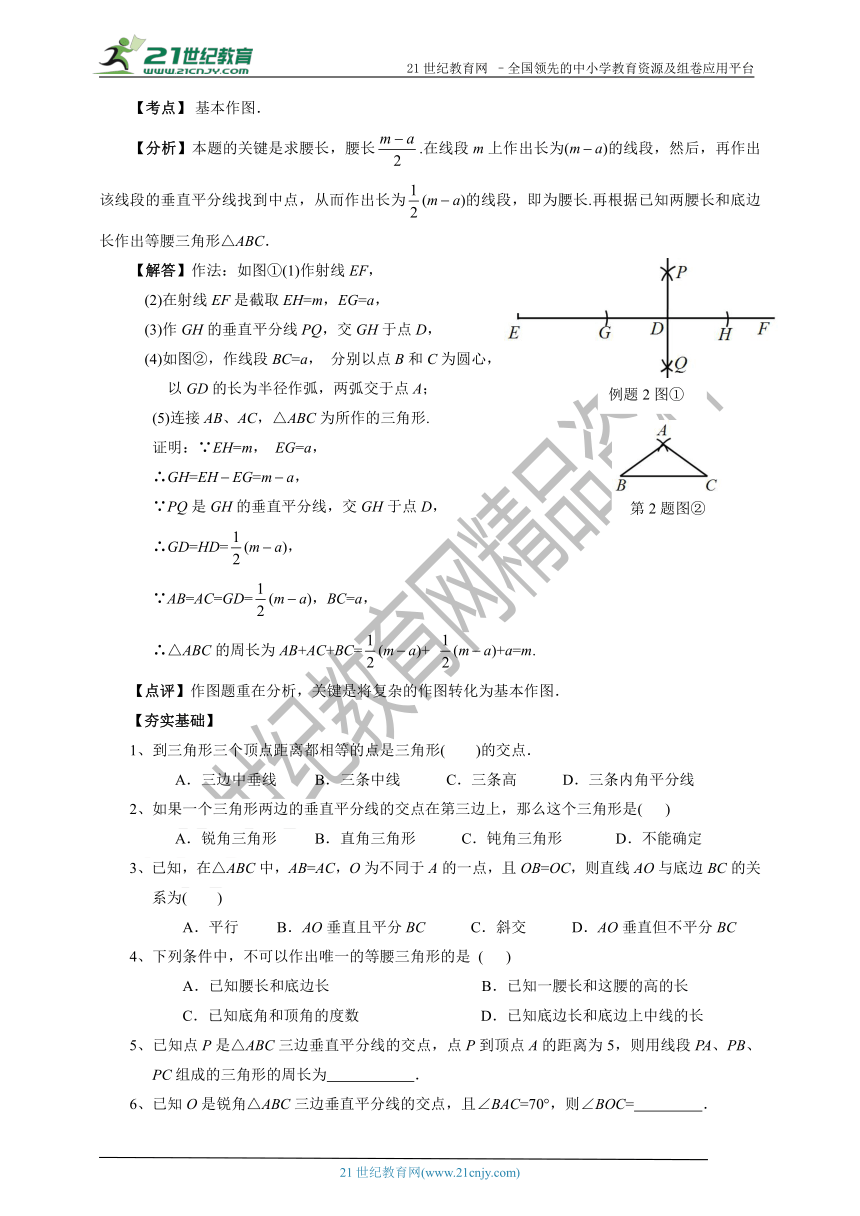
例题2、如图,已知线段a,m(m>2a).
求作:△ABC,使AB=AC,BC=a,周长为m.
【考点】?基本作图.
【分析】本题的关键是求腰长,腰长.在线段m上作出长为(ma)的线段,然后,再作出该线段的垂直平分线找到中点,从而作出长为(ma)的线段,即为腰长.再根据已知两腰长和底边长作出等腰三角形△ABC.
【解答】作法:如图①(1)作射线EF,
(2)在射线EF是截取EH=m,EG=a,
(3)作GH的垂直平分线PQ,交GH于点D,
(4)如图②,作线段BC=a,
分别以点B和C为圆心,
以GD的长为半径作弧,两弧交于点A;
(5)连接AB、AC,△ABC为所作的三角形.
证明:∵EH=m,
EG=a,
∴GH=EHEG=ma,
∵PQ是GH的垂直平分线,交GH于点D,
∴GD=HD=(ma),
∵AB=AC=GD=(ma),BC=a,
∴△ABC的周长为AB+AC+BC=(ma)+
(ma)+a=m.
【点评】作图题重在分析,关键是将复杂的作图转化为基本作图.
【夯实基础】
1、到三角形三个顶点距离都相等的点是三角形( )的交点.
A.三边中垂线
B.三条中线
C.三条高
D.三条内角平分线
2、如果一个三角形两边的垂直平分线的交点在第三边上,那么这个三角形是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定
3、已知,在△ABC中,AB=AC,O为不同于A的一点,且OB=OC,则直线AO与底边BC的关系为( )
A.平行
B.AO垂直且平分BC
C.斜交
D.AO垂直但不平分BC
4、下列条件中,不可以作出唯一的等腰三角形的是
(
)
A.已知腰长和底边长
B.已知一腰长和这腰的高的长
C.已知底角和顶角的度数
D.已知底边长和底边上中线的长
5、已知点P是△ABC三边垂直平分线的交点,点P到顶点A的距离为5,则用线段PA、PB、PC组成的三角形的周长为
?.
6、已知O是锐角△ABC三边垂直平分线的交点,且∠BAC=70°,则∠BOC=
.
7、在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得的锐角为50°,则∠B=
.
8、如图,已知线段a,h.求作:△ABC,使AB=AC,BC=a,BC上的高为h.
9、如图,已知:在△ABC中,AB,BC边上的垂直平分线相交于点P,
求证:点P在AC的垂直平分线上.
【提优特训】
10、如图,已知点O是△ABC三边垂直平分线的交点,连接OA、OB、OC,若∠BAO=14°,则∠ACB等于(
)?
?A.96°
B.86°
C.78°
D.76°
11、如图,在△ABC中,∠B=45°,∠C=60°,AC=8,则AB的长为(
)
A.
B.4+
C.
D.12
12、已知在△ABC中,AB=AC,AB的垂直平分线交线段AC于D,若△ABC和△DBC
的周长分别是68cm和50cm,则△ABC的腰长和底边BC的长分别是(
)
?A.18?cm和36?cm?
???B.18?cm和32?cm?
C.32?cm和18?cm?
??D.16?cm和38?cm?
13、如图所示,A,B是直线l外两点,在l上求作一点P,使PA+PB最小,其作法是(
)
?
?A.连接BA并延长与l的交点为P?
B.连接AB,并作线段AB的垂直平分线与l的交点为P
C.过点B作l的垂线,垂线与l的交点为P?
D.过点A作l的垂线段AO,O是垂足,延长AO到A′,
使A′O=AO,再连接A′B,则A′B与l的交点为P
?
14、如图,△ABC中,∠C=90°,DE是AB的中垂线,交BC于点E,交AB于点D,若AE是∠BAC的平分线,则∠B=
.
15、已知如图,在△ABC中,BC=21,AB的中垂线交BC于P,AC的中垂线交BC于Q,则
△APQ的周长
.
16、如图,在Rt△ABC中,∠ACB=90°,AB=2BC,在直线BC或AC上取一点P,使得△PAB
为等腰三角形,则符合条件的点P共有
个.
17、为了推进农村新型合作医疗制度改革,准备在某镇新建一个医疗点P,使P到该镇所属A村、B村、C村的村委会所在地的距离都相等(A、B、C不在同一直线上,地理位置如下图).
(1)请你用尺规作图的方法确定点P的位置.(要求:写出已知、求作;不写作法,保留作
图痕迹);
??
(2)若两村之间距离分别为:AB=5km,AC=5km,BC=6km,求医疗点P到各村的距离.
18、如图,
在△ABC中,AB=BC,∠ABC=90?,E是AB的中点,过点B作CE的垂线,垂足为点G,与过点A与BC的平行的直线相交于点D,
(1)求证:BE=AD;
(2)求证:AC是线段ED的垂直平分线;
(3)试问△DBC是等腰三角形吗?并说明理由.
【中考链接】
19、(2020?吉林长春)如图,在△ABC中,∠BAC=90°,AB>AC.按下列步骤作图:
?①分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,
②作直线MN,与边AB相交于点D,连结CD.
?
下列说法不一定正确的是(
)
A.∠BDN=∠CDN
B.∠ADC=2∠B
C.∠ACD=∠DCB
D.2∠B+∠ACD=90°
?
20、(2020?哈尔滨)如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB'关于直线AD对称,点B的对称点是点B',则∠CA
B'的度数为(
)
A.10°?
B.20°
?C.30°
?D.40°
21、
(2020?湖北十堰)如图,在△ABC中,DE是AC的垂直平分线.若AE3,△ABD的周长
为13,则△ABC的周长为
.
22、(2020?湖南永州)∠AOB在平面直角坐标系中的位置如图所示,且∠AOB=60°,在∠AOB内有一点P(4,3),M,N分别是OA,OB边上的动点,连接PM,PN,MN,则△PMN的周长的最小值是
.
参考答案
1、A
2、B
3、B
4、C
5、15
6、140°
7、70°或20°
10、D
11、A
12、C
13、D
14、30°
15、21
16、6
19、C
20、A
21、19
22、
8、如图,已知线段a,h.求作:△ABC,使AB=AC,BC=a,BC上的高为h.
作法:(1)作线段BC=a,
(2)作线段BC的垂直平分线MN,
交BC于点D,
(3)在射线DM上截取DA=h,
(4)连接AB、AC,
△ABC为所求作的三角形.
9、如图,已知:在△ABC中,AB,BC边上的垂直平分线相交于点P,
求证:点P在AC的垂直平分线上.
证明:连接PA、PB、PC.
∵边AB,BC的垂直平分线交于点P,
∴PA=PB,PB=PC.
∴PA=PB=PC.
∴点P必在AC的垂直平分线上.
17、为了推进农村新型合作医疗制度改革,准备在某镇新建一个医疗点P,使P到该镇所属A村、B村、C村的村委会所在地的距离都相等(A、B、C不在同一直线上,地理位置如下图).
(1)请你用尺规作图的方法确定点P的位置.(要求:写出已知、求作;不写作法,保留作
图痕迹);
??
(2)若两村之间距离分别为:AB=5km,AC=5km,BC=6km,求医疗点P到各村的距离.
(1)已知:A、B、C三点不在同一直线上.
求作:一点P,使PA=PB=PC.
作图:如图(1)
(2)如图(2),
∵点P是AB和BC垂直平分线的交点,
∴BP=AP,且AD⊥BC于D,
∵AB=AC=5km,
AC=6km,
∴点D为BC的中点,
∴BD=CD==3(km),
在Rt△ABD中,AD=(km),
设PB=x,则PB=PA=x,PD=4x,
在Rt△PBD中,BD2+PD2=PB2,
∴32+(4x)2=x2,
解方程得,x=(km),
∴PB=(km).
∴医疗点P到各村的距离km.
18、如图,
在△ABC中,AB=BC,∠ABC=90?,E是AB的中点,过点B作CE的垂线,垂足为点G,与过点A与BC的平行的直线相交于点D,
(1)求证:BE=AD;
(2)求证:AC是线段ED的垂直平分线;
(3)试问△DBC是等腰三角形吗?并说明理由.
证明(1)∵CE⊥BD,∠ABC=90?,
∴∠2+∠3=90?、∠1+∠1=90?
∴∠1=∠2
又∵AD∥BC,∠DAB=∠ABC=90°,
∴∠DAB=∠EBC=90°,
在△ABD和△BCE中,
∵,
∴△ABD≌△BCE
(ASA),
∴BE=AD;
(2)∵E是AB的中点,
∴AE=BD,
∴AE=AD,
∵AB=BC、∠EBC=∠DAB=90°,
∴∠EAC=∠DAC=45°.
又∵AC=AC,
∴△ACE≌△ACD,
∴CE=CD,
∴AC是线段ED的垂直平分线;
(3)由(1)(2)知DB=EC、DC=EC,
∴DB=DC,
∴△DBC是等腰三角形.
第9题图
例题1图
第2题图②
第14题图
第17题图(1)
第17题图
第15题图
第17题图(2)
第9题图
第19题图
例题2图②
第22题图
第13题图
第8题图
第8题图
图1
例题2图
第10题图
第8题图
第18题图
第11题图
例题2图①
第21题图
第17题图
第18题图
第19题图
第20题图
例题1图
第16题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
–全国领先的中小学教育资源及组卷应用平台
北师大版八年级数学下册第1章三角形的证明
1.3
线段的垂直平分线
第2课时
线段的垂直平分线2
【知识清单】
1、三角形三边垂直平分线性质:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.当三角形是锐角三角形时,交点在其内部;当三角形
是钝角三角形时,交点在其外部;当三角形是直角三角形时,交点
在其斜边的中点上.
2、线段的垂直平分线的作法及其作用.
(1)线段的垂直平分线的作法:
已知:线段AB(如图1所示),求作线段AB的垂直平分线.
作法:①分别以点A和B为圆心,以大于的长为半径作弧,
两弧交于点C和D;
②作直线CD.直线CD就是线段AB的垂直平分线(直线CD与AB的交点就是线段AB的中点).
(2)这个基本作图的另一个作用就是找已知线段的中点.
【经典例题】
例题1、如图所示,A、B、C三点表示三个村庄的地理位置.为了解决吃水难的问题,自来水公司决定在三个村建厂,要求自来水厂到三个村的距离相等.请你设计出自来水厂O点的位置,并说明理由.
【考点】线段垂直平分线的作法和应用.
【分析】根据垂直平分线的性质,作出AB,BC的垂直平分线,两条直线相交于点O,点O位置即可确定.
【解答】连接AB、AC、BC,
作AB、BC的垂直平分线,两线交于点O,
点O就是自来水厂的位置.
根据线段垂直平分线上的点到线段两端点的距离相等可得OA=OB=OC.
【点评】此题主要考查了应用与设计作图,根据垂直平分线的性质得出O点位置是解题关键.
例题2、如图,已知线段a,m(m>2a).
求作:△ABC,使AB=AC,BC=a,周长为m.
【考点】?基本作图.
【分析】本题的关键是求腰长,腰长.在线段m上作出长为(ma)的线段,然后,再作出该线段的垂直平分线找到中点,从而作出长为(ma)的线段,即为腰长.再根据已知两腰长和底边长作出等腰三角形△ABC.
【解答】作法:如图①(1)作射线EF,
(2)在射线EF是截取EH=m,EG=a,
(3)作GH的垂直平分线PQ,交GH于点D,
(4)如图②,作线段BC=a,
分别以点B和C为圆心,
以GD的长为半径作弧,两弧交于点A;
(5)连接AB、AC,△ABC为所作的三角形.
证明:∵EH=m,
EG=a,
∴GH=EHEG=ma,
∵PQ是GH的垂直平分线,交GH于点D,
∴GD=HD=(ma),
∵AB=AC=GD=(ma),BC=a,
∴△ABC的周长为AB+AC+BC=(ma)+
(ma)+a=m.
【点评】作图题重在分析,关键是将复杂的作图转化为基本作图.
【夯实基础】
1、到三角形三个顶点距离都相等的点是三角形( )的交点.
A.三边中垂线
B.三条中线
C.三条高
D.三条内角平分线
2、如果一个三角形两边的垂直平分线的交点在第三边上,那么这个三角形是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定
3、已知,在△ABC中,AB=AC,O为不同于A的一点,且OB=OC,则直线AO与底边BC的关系为( )
A.平行
B.AO垂直且平分BC
C.斜交
D.AO垂直但不平分BC
4、下列条件中,不可以作出唯一的等腰三角形的是
(
)
A.已知腰长和底边长
B.已知一腰长和这腰的高的长
C.已知底角和顶角的度数
D.已知底边长和底边上中线的长
5、已知点P是△ABC三边垂直平分线的交点,点P到顶点A的距离为5,则用线段PA、PB、PC组成的三角形的周长为
?.
6、已知O是锐角△ABC三边垂直平分线的交点,且∠BAC=70°,则∠BOC=
.
7、在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得的锐角为50°,则∠B=
.
8、如图,已知线段a,h.求作:△ABC,使AB=AC,BC=a,BC上的高为h.
9、如图,已知:在△ABC中,AB,BC边上的垂直平分线相交于点P,
求证:点P在AC的垂直平分线上.
【提优特训】
10、如图,已知点O是△ABC三边垂直平分线的交点,连接OA、OB、OC,若∠BAO=14°,则∠ACB等于(
)?
?A.96°
B.86°
C.78°
D.76°
11、如图,在△ABC中,∠B=45°,∠C=60°,AC=8,则AB的长为(
)
A.
B.4+
C.
D.12
12、已知在△ABC中,AB=AC,AB的垂直平分线交线段AC于D,若△ABC和△DBC
的周长分别是68cm和50cm,则△ABC的腰长和底边BC的长分别是(
)
?A.18?cm和36?cm?
???B.18?cm和32?cm?
C.32?cm和18?cm?
??D.16?cm和38?cm?
13、如图所示,A,B是直线l外两点,在l上求作一点P,使PA+PB最小,其作法是(
)
?
?A.连接BA并延长与l的交点为P?
B.连接AB,并作线段AB的垂直平分线与l的交点为P
C.过点B作l的垂线,垂线与l的交点为P?
D.过点A作l的垂线段AO,O是垂足,延长AO到A′,
使A′O=AO,再连接A′B,则A′B与l的交点为P
?
14、如图,△ABC中,∠C=90°,DE是AB的中垂线,交BC于点E,交AB于点D,若AE是∠BAC的平分线,则∠B=
.
15、已知如图,在△ABC中,BC=21,AB的中垂线交BC于P,AC的中垂线交BC于Q,则
△APQ的周长
.
16、如图,在Rt△ABC中,∠ACB=90°,AB=2BC,在直线BC或AC上取一点P,使得△PAB
为等腰三角形,则符合条件的点P共有
个.
17、为了推进农村新型合作医疗制度改革,准备在某镇新建一个医疗点P,使P到该镇所属A村、B村、C村的村委会所在地的距离都相等(A、B、C不在同一直线上,地理位置如下图).
(1)请你用尺规作图的方法确定点P的位置.(要求:写出已知、求作;不写作法,保留作
图痕迹);
??
(2)若两村之间距离分别为:AB=5km,AC=5km,BC=6km,求医疗点P到各村的距离.
18、如图,
在△ABC中,AB=BC,∠ABC=90?,E是AB的中点,过点B作CE的垂线,垂足为点G,与过点A与BC的平行的直线相交于点D,
(1)求证:BE=AD;
(2)求证:AC是线段ED的垂直平分线;
(3)试问△DBC是等腰三角形吗?并说明理由.
【中考链接】
19、(2020?吉林长春)如图,在△ABC中,∠BAC=90°,AB>AC.按下列步骤作图:
?①分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,
②作直线MN,与边AB相交于点D,连结CD.
?
下列说法不一定正确的是(
)
A.∠BDN=∠CDN
B.∠ADC=2∠B
C.∠ACD=∠DCB
D.2∠B+∠ACD=90°
?
20、(2020?哈尔滨)如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB'关于直线AD对称,点B的对称点是点B',则∠CA
B'的度数为(
)
A.10°?
B.20°
?C.30°
?D.40°
21、
(2020?湖北十堰)如图,在△ABC中,DE是AC的垂直平分线.若AE3,△ABD的周长
为13,则△ABC的周长为
.
22、(2020?湖南永州)∠AOB在平面直角坐标系中的位置如图所示,且∠AOB=60°,在∠AOB内有一点P(4,3),M,N分别是OA,OB边上的动点,连接PM,PN,MN,则△PMN的周长的最小值是
.
参考答案
1、A
2、B
3、B
4、C
5、15
6、140°
7、70°或20°
10、D
11、A
12、C
13、D
14、30°
15、21
16、6
19、C
20、A
21、19
22、
8、如图,已知线段a,h.求作:△ABC,使AB=AC,BC=a,BC上的高为h.
作法:(1)作线段BC=a,
(2)作线段BC的垂直平分线MN,
交BC于点D,
(3)在射线DM上截取DA=h,
(4)连接AB、AC,
△ABC为所求作的三角形.
9、如图,已知:在△ABC中,AB,BC边上的垂直平分线相交于点P,
求证:点P在AC的垂直平分线上.
证明:连接PA、PB、PC.
∵边AB,BC的垂直平分线交于点P,
∴PA=PB,PB=PC.
∴PA=PB=PC.
∴点P必在AC的垂直平分线上.
17、为了推进农村新型合作医疗制度改革,准备在某镇新建一个医疗点P,使P到该镇所属A村、B村、C村的村委会所在地的距离都相等(A、B、C不在同一直线上,地理位置如下图).
(1)请你用尺规作图的方法确定点P的位置.(要求:写出已知、求作;不写作法,保留作
图痕迹);
??
(2)若两村之间距离分别为:AB=5km,AC=5km,BC=6km,求医疗点P到各村的距离.
(1)已知:A、B、C三点不在同一直线上.
求作:一点P,使PA=PB=PC.
作图:如图(1)
(2)如图(2),
∵点P是AB和BC垂直平分线的交点,
∴BP=AP,且AD⊥BC于D,
∵AB=AC=5km,
AC=6km,
∴点D为BC的中点,
∴BD=CD==3(km),
在Rt△ABD中,AD=(km),
设PB=x,则PB=PA=x,PD=4x,
在Rt△PBD中,BD2+PD2=PB2,
∴32+(4x)2=x2,
解方程得,x=(km),
∴PB=(km).
∴医疗点P到各村的距离km.
18、如图,
在△ABC中,AB=BC,∠ABC=90?,E是AB的中点,过点B作CE的垂线,垂足为点G,与过点A与BC的平行的直线相交于点D,
(1)求证:BE=AD;
(2)求证:AC是线段ED的垂直平分线;
(3)试问△DBC是等腰三角形吗?并说明理由.
证明(1)∵CE⊥BD,∠ABC=90?,
∴∠2+∠3=90?、∠1+∠1=90?
∴∠1=∠2
又∵AD∥BC,∠DAB=∠ABC=90°,
∴∠DAB=∠EBC=90°,
在△ABD和△BCE中,
∵,
∴△ABD≌△BCE
(ASA),
∴BE=AD;
(2)∵E是AB的中点,
∴AE=BD,
∴AE=AD,
∵AB=BC、∠EBC=∠DAB=90°,
∴∠EAC=∠DAC=45°.
又∵AC=AC,
∴△ACE≌△ACD,
∴CE=CD,
∴AC是线段ED的垂直平分线;
(3)由(1)(2)知DB=EC、DC=EC,
∴DB=DC,
∴△DBC是等腰三角形.
第9题图
例题1图
第2题图②
第14题图
第17题图(1)
第17题图
第15题图
第17题图(2)
第9题图
第19题图
例题2图②
第22题图
第13题图
第8题图
第8题图
图1
例题2图
第10题图
第8题图
第18题图
第11题图
例题2图①
第21题图
第17题图
第18题图
第19题图
第20题图
例题1图
第16题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
