2020-2021学年人教版九年级数学下册 第27章:相似 精选提升练习(四)(word版含解析)
文档属性
| 名称 | 2020-2021学年人教版九年级数学下册 第27章:相似 精选提升练习(四)(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 164.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 09:19:40 | ||
图片预览



文档简介
2020-2021学年人教版九年级数学下册
第27章:相似
精选提升练习(四)
1.如图所示,在等腰△ABC中,AB=AC=5cm,BC=8cm,点P由点A出发沿AB方向向点B匀速运动,同时点Q由点B出发沿BC方向向点C匀速运动,它们的速度均为1cm/s.连接PQ,设运动时间为t(s)(0<t<5),解答下列问题:
(1)当t为何值时,△BPQ的面积为cm2;
(2)在点P,Q的运动中,是否存在时间t,使△BPQ为等腰三角形.若存在,请求出对应的时间t;若不存在,请说明理由.
2.如图,在四边形ABCD中,∠ACB=∠ADC=90°,AC平分∠BAD,过点C作CE∥AD交AB于点E,连接DE交AC于点F.
(1)求证:AC2=AB?AD;
(2)若AB=4,AD=3,求EF的长.
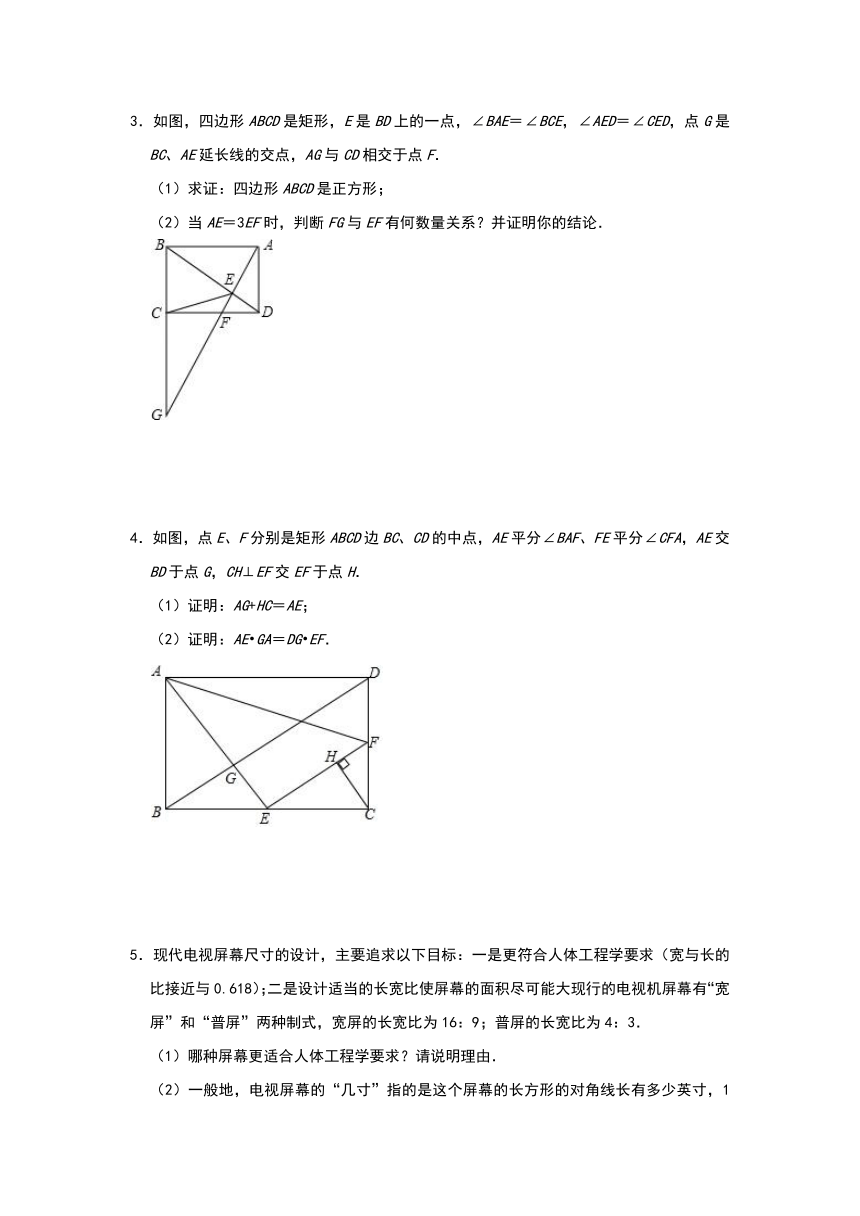
3.如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC、AE延长线的交点,AG与CD相交于点F.
(1)求证:四边形ABCD是正方形;
(2)当AE=3EF时,判断FG与EF有何数量关系?并证明你的结论.
4.如图,点E、F分别是矩形ABCD边BC、CD的中点,AE平分∠BAF、FE平分∠CFA,AE交BD于点G,CH⊥EF交EF于点H.
(1)证明:AG+HC=AE;
(2)证明:AE?GA=DG?EF.
5.现代电视屏幕尺寸的设计,主要追求以下目标:一是更符合人体工程学要求(宽与长的比接近与0.618);二是设计适当的长宽比使屏幕的面积尽可能大现行的电视机屏幕有“宽屏”和“普屏”两种制式,宽屏的长宽比为16:9;普屏的长宽比为4:3.
(1)哪种屏幕更适合人体工程学要求?请说明理由.
(2)一般地,电视屏幕的“几寸”指的是这个屏幕的长方形的对角线长有多少英寸,1英寸=2.54cm,小明家想买80寸的宽屏电视机(边框宽都为1cm),并嵌入到墙中.则需要预留的长方形位置的长、宽各多少cm?(最后结果保留到整数,≈18.4,≈5.8)
(3)在相同尺寸的电视机屏幕中,宽屏的屏幕面积大还是普屏的屏幕面积大?请说明理由.
6.已知,如图在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P由点A出发沿AB方向向终点点B匀速移动,速度为1cm/s,点Q由点B出发沿BC方向向终点点C匀速移动,速度为2cm/s.如果动点P,Q同时从A,B出发,当P或Q到达终点时运动停止.几秒后,以Q,B,P为顶点的三角形与△ABC相似?
7.如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E,连接OE.
(1)求证:△DBE是等腰三角形;
(2)求证:△COE∽△CAB.
8.从三角形(不是等腰三角形)一个顶点引起一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,∠A=48°,CD是△ABC的完美分割线,且AD=CD,求∠ACB的度数.
(2)如图2,在△ABC中,AC=2,BC=,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,找出CD与BD的关系.
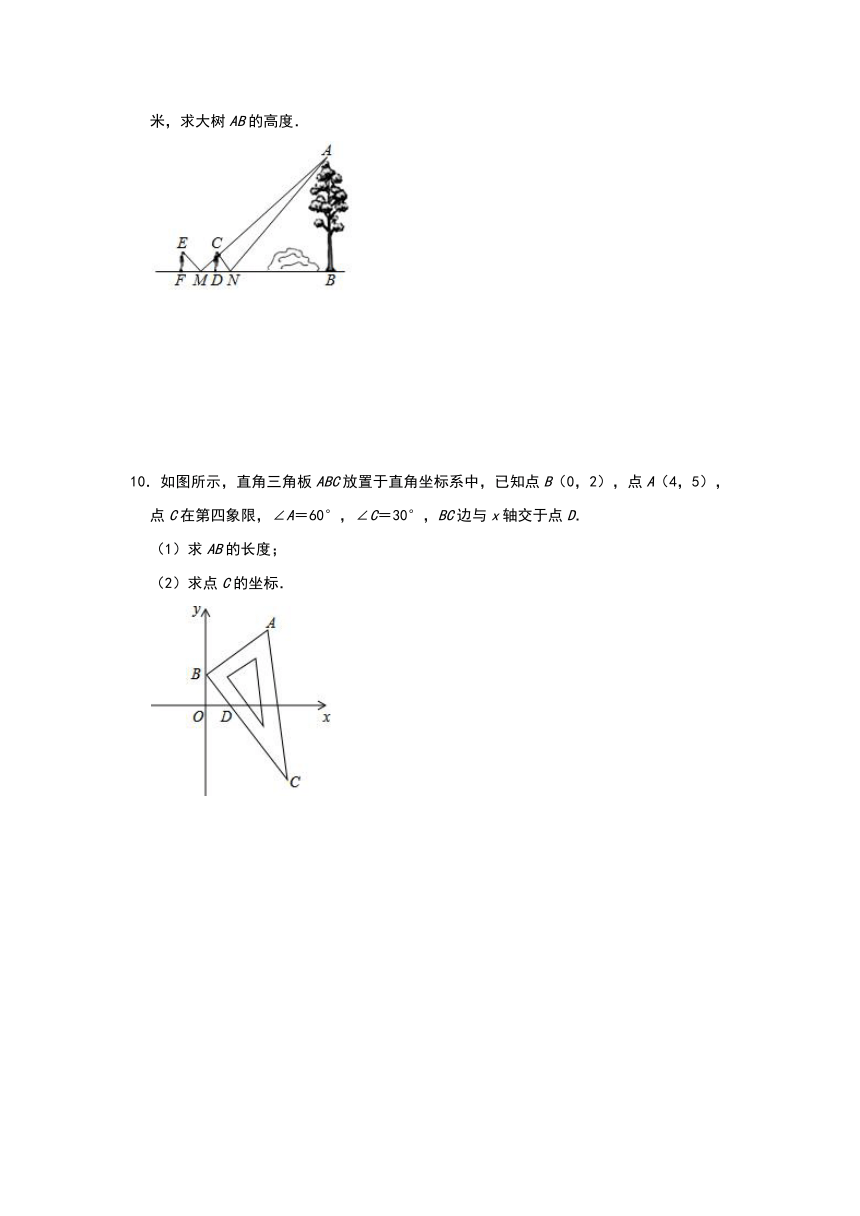
9.“创新实践”小组想利用镜子与皮尺测量大树AB的高度,因大树底部有障碍物,无法直接测量到大树底部的距离.聪明的小颖借鉴《海岛算经》的测量方法设计出如图所示的测量方案:测量者站在点F处,将镜子放在点M处时,刚好看到大树的顶端,沿大树方向向前走3米,到达点D处,将镜子放在点N处时,刚好看到大树的顶端(点F,M,D,N,B在同一条直线上),若测得FM=1.5米,DN=1米,测量者眼睛到地面的距离为1.6米,求大树AB的高度.
10.如图所示,直角三角板ABC放置于直角坐标系中,已知点B(0,2),点A(4,5),点C在第四象限,∠A=60°,∠C=30°,BC边与x轴交于点D.
(1)求AB的长度;
(2)求点C的坐标.
参考答案
1.解:(1)如图,过点A作AE⊥BC于E,过点P作PF⊥BC于F,
∵AB=AC=5cm,BC=8cm,AE⊥BC,
∴BE=EC=4cm,
∴AE===3cm,
∵∠PFB=∠AEB=90°,∠B=∠B,
∴△AEB∽△PFB,
∴=,
∴=,
∴PF=cm,BF=cm,
∵△BPQ的面积为cm2,
∴×BQ×PF=,
∴×t×=,
∴t1=1,t2=4,
∴当t为1或4时,△BPQ的面积为cm2;
(2)当BP=BQ时,则5﹣t=t,
∴t=,
当BQ=PQ时,∵PQ2=PF2+QF2,
∴t2=[]2+[﹣t]2,
∴t1=5(不合题意),t2=,
当BP=PQ时,则点P在BF的垂直平分线上,
∴=,
∴t=,
综上所述:t的值为或或时,△BPQ为等腰三角形.
2.(1)证明:∵AC平分∠BAD,
∴∠BAC=∠CAD,
∵∠ACB=∠ADC=90°,
∴△ACB∽△ADC,
∴,
∴AC2=AB?AD;
(2)解:∵AB=4,AD=3,
∴AC=6,
∴==2,
∴,
∴∠BAC=30°,
∴∠BAC=∠CAD=30°,
∵∠ACB=∠ADC=90°,
∴∠B=∠ACD=60°,
∵CE∥AD,
∴∠ECA=∠CAD=30°,
∠BCE=∠ACB﹣∠ECA=60°,
∴△BCE是等边三角形,
∴,
在Rt△ADC中,∠CAD=30°,
∴,
∵CE∥AD,
∴∠DCE=180°﹣∠ADC=90°,
∴==.
∵CE∥AD,
∴△CEF∽△ADF,
∴,
∴,
∵,
∴.
3.(1)证明:∵四边形ABCD是矩形,
∴∠BAD=∠BCD=90°,
∵∠BAE=∠BCE,
∴∠BAD﹣∠BAE=∠BCD﹣∠BCE,
即∠DAE=∠DCE,
在△AED和△CED中,
,
∴△AED≌△CED(AAS),
∴AD=CD,
∵四边形ABCD是矩形,
∴四边形ABCD是正方形;
(2)当AE=3EF时,FG=8EF.
证明:设EF=k,则AE=3k
∵△AED≌△CED,
∴CE=AE=3k,
∵四边形ABCD是正方形,
∴AD∥BC,
∴∠G=∠DAE,
又∵∠DAE=∠DCE,
∴∠DCE=∠G,
又∵∠CEF=∠GEC,
∴△CEF∽△GEC,
∴,
∴,
∴EG=9k,
∴FG=EG﹣EF=8k,
∴FG=8EF.
4.证明:(1)∵E、F分别是矩形ABCD边BC、CD的中点,
∴EF∥BD,
∴∠HEC=∠BGE,
∵AE平分∠BAF、FE平分∠CFA,
∴,,
∵AB∥CD,
∴∠BAF+∠AFC=180°,
∴∠EAF+∠AFE=90°,
∴∠AEF=90°,
∴∠BGE=90°,
∵BE=EC,
∴△BGE≌△EHC(AAS),
∴GE=HC,
∴AG+GE=AG+HC=AE;
(2)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ADB=∠GBE,
∵∠GBE=∠BAE=∠EAF,
∴∠EAF=∠ADG,
∵∠AEF=∠AGD=90°,
∴△DAG∽△AEF,
∴,
即AE?GA=DG?EF.
5.解:(1)=0.5625,=0.75,
∵0.5625与0.618接近,
∴宽屏更适合人体工程学要求.
(2)设宽屏电视机的长为16xcm,宽为9xcm.
则对角线的长==18.4x(cm),
由题意18.4x=80×2.54,
∴x≈11.04,
∴宽屏电视机的长为176.64cm,宽为99.36cm,
根据进一法,可得宽屏电视机的长为177cm,宽为100cm,
∵边框宽都为1cm,
∴预留的长方形位置的长、宽分别为:178cm,101cm.
(3)设对角线的长为5a.则普屏的电视机的面积为12a2,
设宽屏电视机的长为16y,宽为9y,则对角线=18.4y=5a,
∴y=0.27a,
∴宽屏电视机的面积=144y2≈10.5a2<12a2,
∴在相同尺寸的电视机屏幕中,普屏的屏幕面积大.
6.解:设t秒后,以Q,B,P为顶点的三角形与△ABC相似;
则PB=(6﹣t)cm,BQ=2tcm,
∵∠B=90°,
∴分两种情况:
①当时,
即,
解得:t=2.4;
②当时,
即,
解得:t=;
综上所述:2.4秒或秒时,以Q,B,P为顶点的三角形与△ABC相似.
7.证明:(1)连接OD,如图所示:
∵DE是⊙O的切线,
∴∠ODE=90°,
∴∠ADO+∠BDE=90°,
∵∠ACB=90°,
∴∠CAB+∠CBA=90°,
∵OA=OD,
∴∠CAB=∠ADO,
∴∠BDE=∠CBA,
∴EB=ED,
∴△DBE是等腰三角形;
(2)∵∠ACB=90°,AC是⊙O的直径,
∴CB是⊙O的切线,
∵DE是⊙O的切线,
∴DE=EC,
∵EB=ED,
∴EC=EB,
∵OA=OC,
∴OE∥AB,
∴△COE∽△CAB.
8.解:(1)当AD=CD时,如图3,∠ACD=∠A=48°,
∵△BDC∽△BCA,
∴∠BCD=∠A=48°,
∴∠ACB=∠ACD+∠BCD=96°.
(2)结论:CD=BD.
∵△BCD∽△BAC,
∵△BCD∽△BAC,
∴=,
∴==,
∴CD=BD.
9.解:设NB的长为x米,则MB=x+1+3﹣1.5=(x+2.5)米.
由题意,得∠CND=∠ANB,∠CDN=∠ABN=90°,
∴△CND∽△ANB,
∴=.
同理,△EMF∽△AMB,
∴=.
∵EF=CD,
∴=,即=.
解得x=5,
∵=,
∴=.
解得AB=8.
答:大树AB的高度为8米.
10.解:(1)过点A作AE⊥y轴于点E,
∵点A(4,5),B(0,2),
∴AE=4,BE=5﹣2=3,
由勾股定理得:=5;
(2)在Rt△ABC中,∵∠A=60°,AB=5,
∴BC=AB
tan
60°=5,
过C作CF⊥y轴于点F,
则∠BFC=∠AEB=90°
∵∠CBF+∠ABE=90°,∠CBF+∠BCF=90°
∴∠BCF=∠ABE,
∴△BFC∽△AEB,
∴,即,
∴,
∵OF=BF﹣OB=
∴点C的坐标为(,).
第27章:相似
精选提升练习(四)
1.如图所示,在等腰△ABC中,AB=AC=5cm,BC=8cm,点P由点A出发沿AB方向向点B匀速运动,同时点Q由点B出发沿BC方向向点C匀速运动,它们的速度均为1cm/s.连接PQ,设运动时间为t(s)(0<t<5),解答下列问题:
(1)当t为何值时,△BPQ的面积为cm2;
(2)在点P,Q的运动中,是否存在时间t,使△BPQ为等腰三角形.若存在,请求出对应的时间t;若不存在,请说明理由.
2.如图,在四边形ABCD中,∠ACB=∠ADC=90°,AC平分∠BAD,过点C作CE∥AD交AB于点E,连接DE交AC于点F.
(1)求证:AC2=AB?AD;
(2)若AB=4,AD=3,求EF的长.
3.如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC、AE延长线的交点,AG与CD相交于点F.
(1)求证:四边形ABCD是正方形;
(2)当AE=3EF时,判断FG与EF有何数量关系?并证明你的结论.
4.如图,点E、F分别是矩形ABCD边BC、CD的中点,AE平分∠BAF、FE平分∠CFA,AE交BD于点G,CH⊥EF交EF于点H.
(1)证明:AG+HC=AE;
(2)证明:AE?GA=DG?EF.
5.现代电视屏幕尺寸的设计,主要追求以下目标:一是更符合人体工程学要求(宽与长的比接近与0.618);二是设计适当的长宽比使屏幕的面积尽可能大现行的电视机屏幕有“宽屏”和“普屏”两种制式,宽屏的长宽比为16:9;普屏的长宽比为4:3.
(1)哪种屏幕更适合人体工程学要求?请说明理由.
(2)一般地,电视屏幕的“几寸”指的是这个屏幕的长方形的对角线长有多少英寸,1英寸=2.54cm,小明家想买80寸的宽屏电视机(边框宽都为1cm),并嵌入到墙中.则需要预留的长方形位置的长、宽各多少cm?(最后结果保留到整数,≈18.4,≈5.8)
(3)在相同尺寸的电视机屏幕中,宽屏的屏幕面积大还是普屏的屏幕面积大?请说明理由.
6.已知,如图在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P由点A出发沿AB方向向终点点B匀速移动,速度为1cm/s,点Q由点B出发沿BC方向向终点点C匀速移动,速度为2cm/s.如果动点P,Q同时从A,B出发,当P或Q到达终点时运动停止.几秒后,以Q,B,P为顶点的三角形与△ABC相似?
7.如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E,连接OE.
(1)求证:△DBE是等腰三角形;
(2)求证:△COE∽△CAB.
8.从三角形(不是等腰三角形)一个顶点引起一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,∠A=48°,CD是△ABC的完美分割线,且AD=CD,求∠ACB的度数.
(2)如图2,在△ABC中,AC=2,BC=,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,找出CD与BD的关系.
9.“创新实践”小组想利用镜子与皮尺测量大树AB的高度,因大树底部有障碍物,无法直接测量到大树底部的距离.聪明的小颖借鉴《海岛算经》的测量方法设计出如图所示的测量方案:测量者站在点F处,将镜子放在点M处时,刚好看到大树的顶端,沿大树方向向前走3米,到达点D处,将镜子放在点N处时,刚好看到大树的顶端(点F,M,D,N,B在同一条直线上),若测得FM=1.5米,DN=1米,测量者眼睛到地面的距离为1.6米,求大树AB的高度.
10.如图所示,直角三角板ABC放置于直角坐标系中,已知点B(0,2),点A(4,5),点C在第四象限,∠A=60°,∠C=30°,BC边与x轴交于点D.
(1)求AB的长度;
(2)求点C的坐标.
参考答案
1.解:(1)如图,过点A作AE⊥BC于E,过点P作PF⊥BC于F,
∵AB=AC=5cm,BC=8cm,AE⊥BC,
∴BE=EC=4cm,
∴AE===3cm,
∵∠PFB=∠AEB=90°,∠B=∠B,
∴△AEB∽△PFB,
∴=,
∴=,
∴PF=cm,BF=cm,
∵△BPQ的面积为cm2,
∴×BQ×PF=,
∴×t×=,
∴t1=1,t2=4,
∴当t为1或4时,△BPQ的面积为cm2;
(2)当BP=BQ时,则5﹣t=t,
∴t=,
当BQ=PQ时,∵PQ2=PF2+QF2,
∴t2=[]2+[﹣t]2,
∴t1=5(不合题意),t2=,
当BP=PQ时,则点P在BF的垂直平分线上,
∴=,
∴t=,
综上所述:t的值为或或时,△BPQ为等腰三角形.
2.(1)证明:∵AC平分∠BAD,
∴∠BAC=∠CAD,
∵∠ACB=∠ADC=90°,
∴△ACB∽△ADC,
∴,
∴AC2=AB?AD;
(2)解:∵AB=4,AD=3,
∴AC=6,
∴==2,
∴,
∴∠BAC=30°,
∴∠BAC=∠CAD=30°,
∵∠ACB=∠ADC=90°,
∴∠B=∠ACD=60°,
∵CE∥AD,
∴∠ECA=∠CAD=30°,
∠BCE=∠ACB﹣∠ECA=60°,
∴△BCE是等边三角形,
∴,
在Rt△ADC中,∠CAD=30°,
∴,
∵CE∥AD,
∴∠DCE=180°﹣∠ADC=90°,
∴==.
∵CE∥AD,
∴△CEF∽△ADF,
∴,
∴,
∵,
∴.
3.(1)证明:∵四边形ABCD是矩形,
∴∠BAD=∠BCD=90°,
∵∠BAE=∠BCE,
∴∠BAD﹣∠BAE=∠BCD﹣∠BCE,
即∠DAE=∠DCE,
在△AED和△CED中,
,
∴△AED≌△CED(AAS),
∴AD=CD,
∵四边形ABCD是矩形,
∴四边形ABCD是正方形;
(2)当AE=3EF时,FG=8EF.
证明:设EF=k,则AE=3k
∵△AED≌△CED,
∴CE=AE=3k,
∵四边形ABCD是正方形,
∴AD∥BC,
∴∠G=∠DAE,
又∵∠DAE=∠DCE,
∴∠DCE=∠G,
又∵∠CEF=∠GEC,
∴△CEF∽△GEC,
∴,
∴,
∴EG=9k,
∴FG=EG﹣EF=8k,
∴FG=8EF.
4.证明:(1)∵E、F分别是矩形ABCD边BC、CD的中点,
∴EF∥BD,
∴∠HEC=∠BGE,
∵AE平分∠BAF、FE平分∠CFA,
∴,,
∵AB∥CD,
∴∠BAF+∠AFC=180°,
∴∠EAF+∠AFE=90°,
∴∠AEF=90°,
∴∠BGE=90°,
∵BE=EC,
∴△BGE≌△EHC(AAS),
∴GE=HC,
∴AG+GE=AG+HC=AE;
(2)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ADB=∠GBE,
∵∠GBE=∠BAE=∠EAF,
∴∠EAF=∠ADG,
∵∠AEF=∠AGD=90°,
∴△DAG∽△AEF,
∴,
即AE?GA=DG?EF.
5.解:(1)=0.5625,=0.75,
∵0.5625与0.618接近,
∴宽屏更适合人体工程学要求.
(2)设宽屏电视机的长为16xcm,宽为9xcm.
则对角线的长==18.4x(cm),
由题意18.4x=80×2.54,
∴x≈11.04,
∴宽屏电视机的长为176.64cm,宽为99.36cm,
根据进一法,可得宽屏电视机的长为177cm,宽为100cm,
∵边框宽都为1cm,
∴预留的长方形位置的长、宽分别为:178cm,101cm.
(3)设对角线的长为5a.则普屏的电视机的面积为12a2,
设宽屏电视机的长为16y,宽为9y,则对角线=18.4y=5a,
∴y=0.27a,
∴宽屏电视机的面积=144y2≈10.5a2<12a2,
∴在相同尺寸的电视机屏幕中,普屏的屏幕面积大.
6.解:设t秒后,以Q,B,P为顶点的三角形与△ABC相似;
则PB=(6﹣t)cm,BQ=2tcm,
∵∠B=90°,
∴分两种情况:
①当时,
即,
解得:t=2.4;
②当时,
即,
解得:t=;
综上所述:2.4秒或秒时,以Q,B,P为顶点的三角形与△ABC相似.
7.证明:(1)连接OD,如图所示:
∵DE是⊙O的切线,
∴∠ODE=90°,
∴∠ADO+∠BDE=90°,
∵∠ACB=90°,
∴∠CAB+∠CBA=90°,
∵OA=OD,
∴∠CAB=∠ADO,
∴∠BDE=∠CBA,
∴EB=ED,
∴△DBE是等腰三角形;
(2)∵∠ACB=90°,AC是⊙O的直径,
∴CB是⊙O的切线,
∵DE是⊙O的切线,
∴DE=EC,
∵EB=ED,
∴EC=EB,
∵OA=OC,
∴OE∥AB,
∴△COE∽△CAB.
8.解:(1)当AD=CD时,如图3,∠ACD=∠A=48°,
∵△BDC∽△BCA,
∴∠BCD=∠A=48°,
∴∠ACB=∠ACD+∠BCD=96°.
(2)结论:CD=BD.
∵△BCD∽△BAC,
∵△BCD∽△BAC,
∴=,
∴==,
∴CD=BD.
9.解:设NB的长为x米,则MB=x+1+3﹣1.5=(x+2.5)米.
由题意,得∠CND=∠ANB,∠CDN=∠ABN=90°,
∴△CND∽△ANB,
∴=.
同理,△EMF∽△AMB,
∴=.
∵EF=CD,
∴=,即=.
解得x=5,
∵=,
∴=.
解得AB=8.
答:大树AB的高度为8米.
10.解:(1)过点A作AE⊥y轴于点E,
∵点A(4,5),B(0,2),
∴AE=4,BE=5﹣2=3,
由勾股定理得:=5;
(2)在Rt△ABC中,∵∠A=60°,AB=5,
∴BC=AB
tan
60°=5,
过C作CF⊥y轴于点F,
则∠BFC=∠AEB=90°
∵∠CBF+∠ABE=90°,∠CBF+∠BCF=90°
∴∠BCF=∠ABE,
∴△BFC∽△AEB,
∴,即,
∴,
∵OF=BF﹣OB=
∴点C的坐标为(,).
