2020-2021学年北师大版八年级数学下册1.1.2《等腰三角形》第2课时 课件(32张PPT)
文档属性
| 名称 | 2020-2021学年北师大版八年级数学下册1.1.2《等腰三角形》第2课时 课件(32张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 315.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 19:35:14 | ||
图片预览





文档简介
第一章三角形的证明
等腰三角形2
复习回顾
我们学过的等腰三角形的性质有哪些?
边:
等腰三角形的两腰相等;
角:
等腰三角形的两底角相等;简述为:等边对等角.
重要线段:
等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合。简述为:“三线合一”
对称性:
等腰三角形是轴对称图形,对称轴只有一条,对称轴是顶角的平分线或底边上的中线或底边上的高所在的直线。
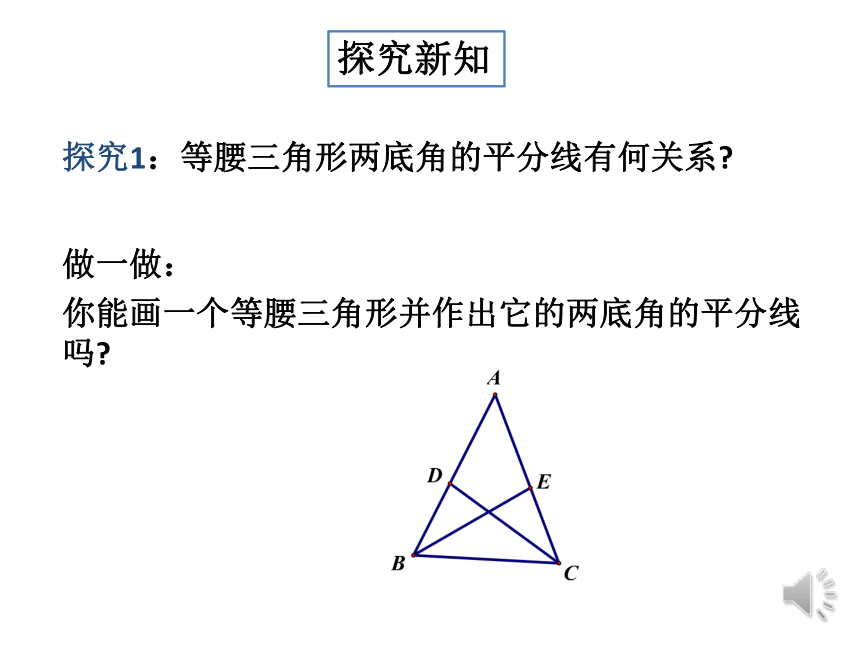
探究新知
你能画一个等腰三角形并作出它的两底角的平分线吗?
探究1:等腰三角形两底角的平分线有何关系?
做一做:
通过观察、测量,可猜想:等腰三角形两底角的平分线
_________.?你能尝试证明你猜想的结论吗?
探究新知
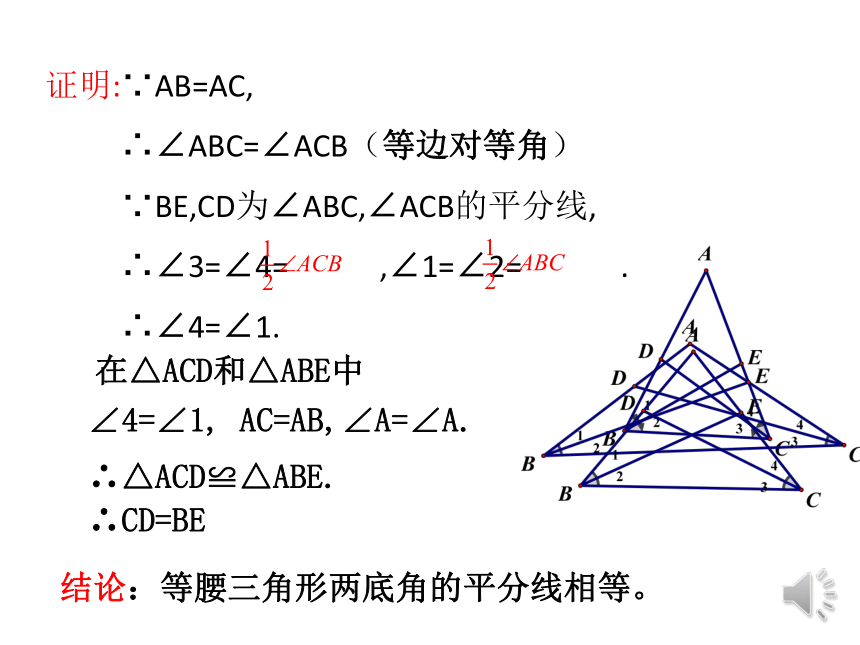
已知:如图,在△ABC中,AB=AC,CD和BE是△ABC的角平分线.
求证:CD=BE.
相等
证明:∵AB=AC,
∴∠ABC=∠ACB(等边对等角)
∵BE,CD为∠ABC,∠ACB的平分线,
∴∠3=∠4= ,∠1=∠2= .
∴∠4=∠1.
∠4=∠1, AC=AB,∠A=∠A.?
∴△ACD≌△ABE.
∴CD=BE?
在△ACD和△ABE中
结论:等腰三角形两底角的平分线相等。
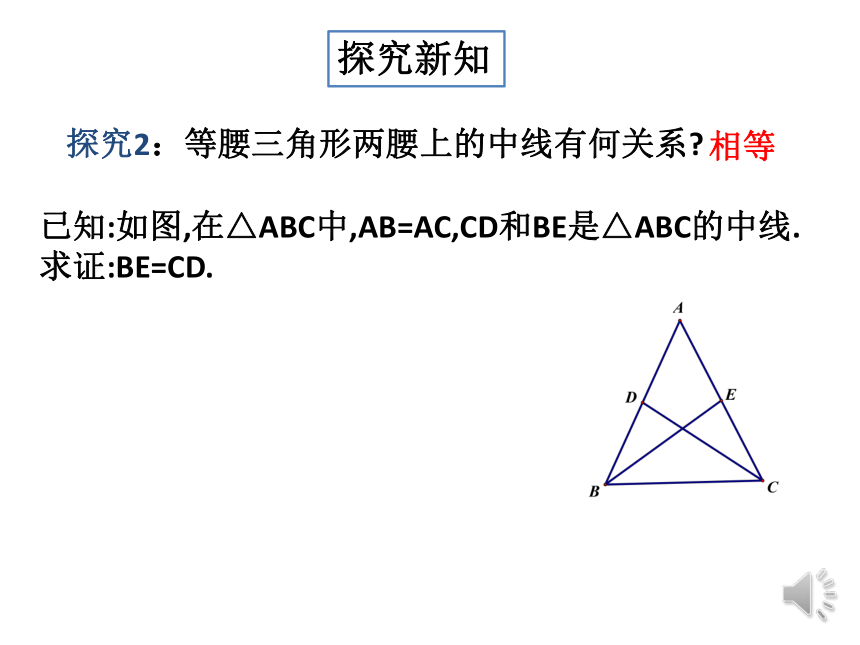
探究2:等腰三角形两腰上的中线有何关系?
探究新知
已知:如图,在△ABC中,AB=AC,CD和BE是△ABC的中线.
求证:BE=CD.
相等
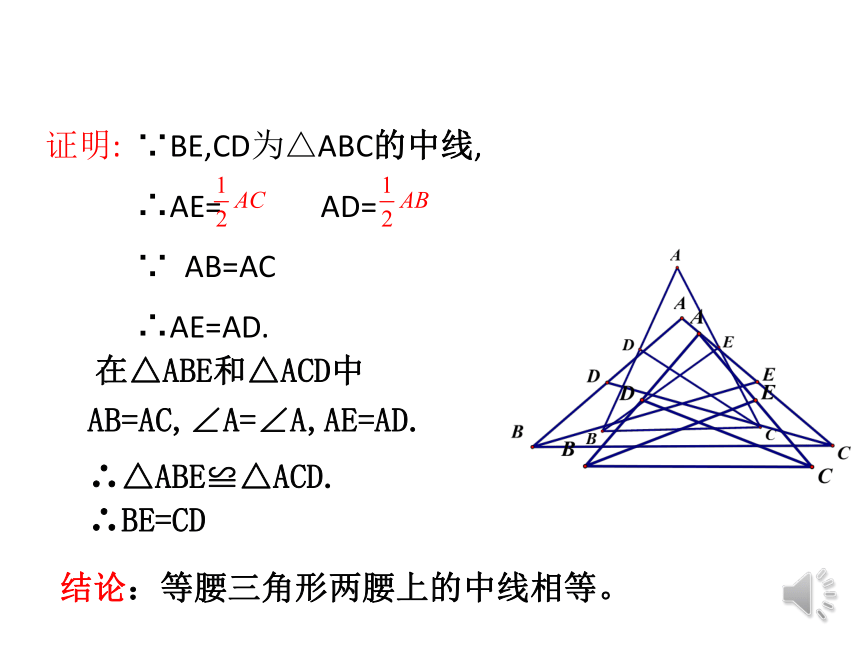
证明: ∵BE,CD为△ABC的中线,
∴AE= AD=
∵ AB=AC
∴AE=AD.
AB=AC,∠A=∠A,AE=AD.?
∴△ABE≌△ACD.
∴BE=CD?
在△ABE和△ACD中
结论:等腰三角形两腰上的中线相等。
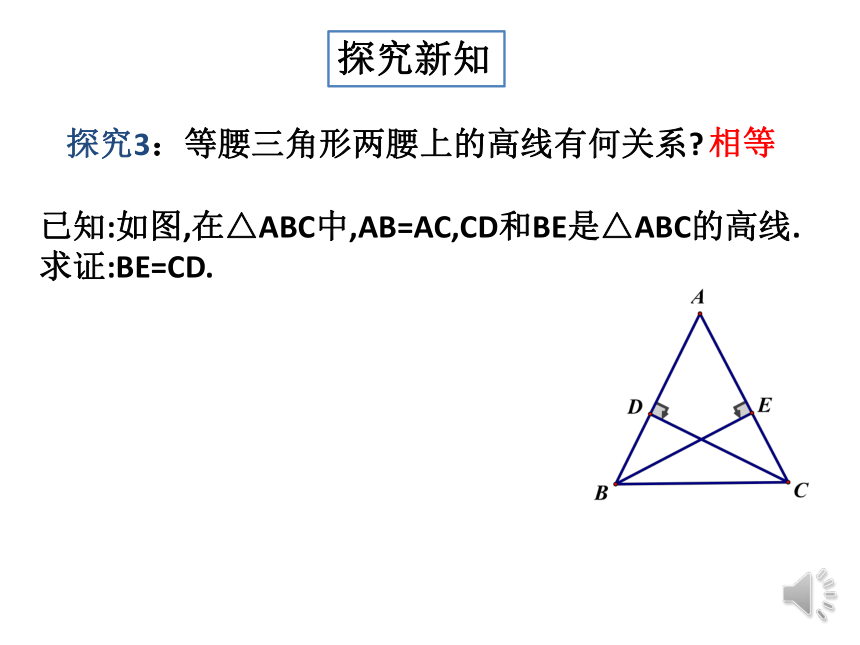
探究3:等腰三角形两腰上的高线有何关系?
探究新知
已知:如图,在△ABC中,AB=AC,CD和BE是△ABC的高线.
求证:BE=CD.
相等
证明: ∵BE,CD为△ABC的高线,
∴
∴
∠AEB=∠ADC,∠A=∠A,AB=AC.?
∴△ABE≌△ACD.
∴BE=CD?
在△ABE和△ACD中
结论:等腰三角形两腰上的高线相等。
D
E
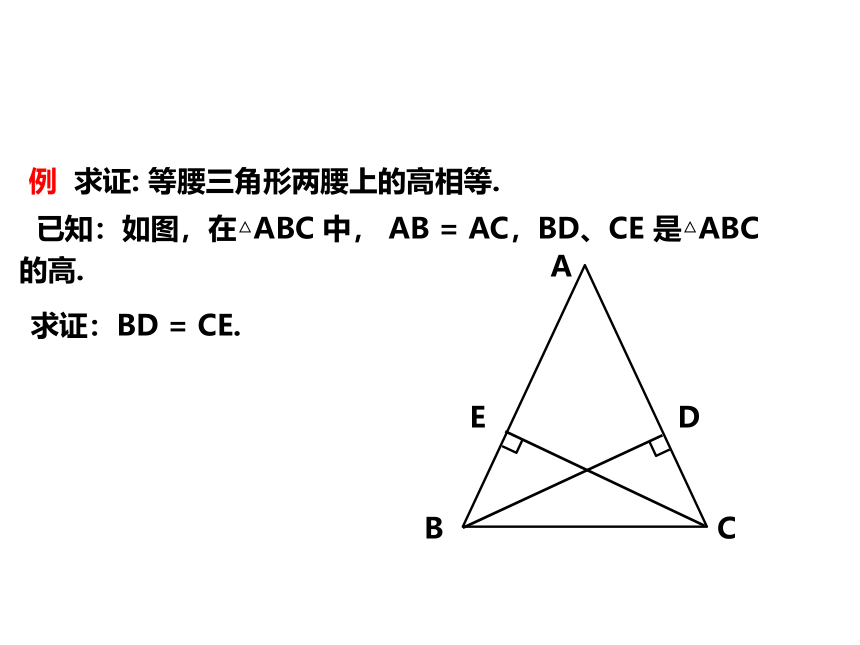
已知:如图,在△ABC 中, AB = AC,BD、CE 是△ABC 的高.
求证:BD = CE.
A
B
C
E
D
例 求证: 等腰三角形两腰上的高相等.
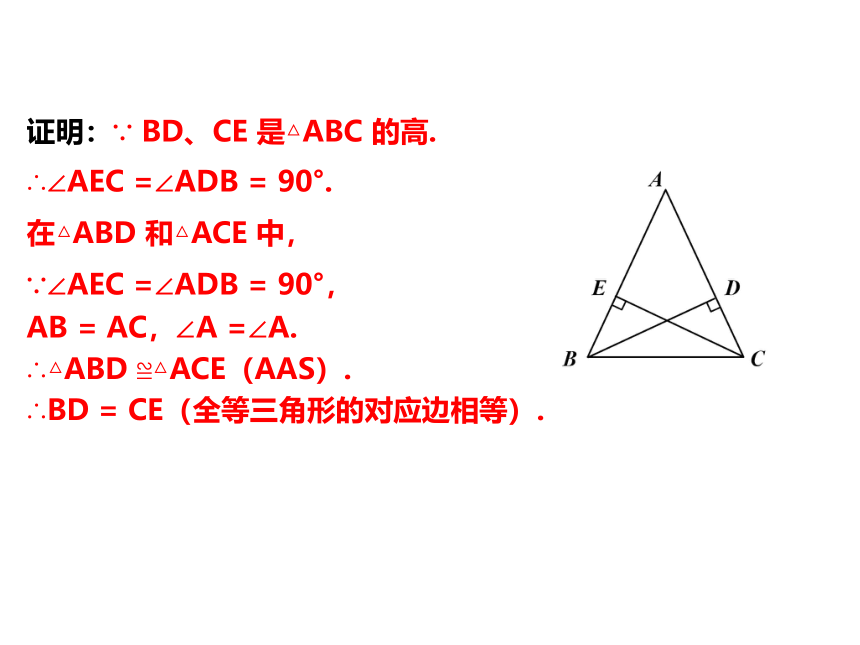
证明:∵ BD、CE 是△ABC 的高.
∴∠AEC =∠ADB = 90°.
在△ABD 和△ACE 中,
∵∠AEC =∠ADB = 90°,
AB = AC,∠A =∠A.
∴△ABD ≌△ACE(AAS).
∴BD = CE(全等三角形的对应边相等).
如图,在△ABC 中,AB = AC,点 D,E 分别在边 AC 和 AB 上.
议一议
E
D
A
B
C
(1)如果∠ABD = ∠ABC,∠ACE = ∠ACB,那么 BD = CE 吗?如果∠ABD = ∠ABC,∠ACE = ∠ACB 呢?由此你能得到一个什么结论?
1
3
1
3
1
4
1
4
E
D
A
B
C
BD = CE
(2)如果 AD = AC,AE = AB,那么 BD = CE 吗?如果 AD = AC,AE = AB 呢?由此你得到什么结论?
1
2
1
2
1
3
1
3
BD = CE
等腰三角形重要线段的结论:
等腰三角形两个底角的平分线_________;?
等腰三角形两腰上的高_________;?
等腰三角形两腰上的中线_________.?
归纳总结
相等
相等
相等
等边三角形的性质
知识点二
等边三角形的定义是什么?
想一想
等边三角形是特殊的等腰三角形,那么等边三角形的内角有什么特征呢?
定理 等边三角形的三个内角都相等,并且每个角都等于60°.
例 已知:如图,在△ABC 中,AB = BC = AC.
求证:∠A =∠B =∠C = 60°.
证明:∵AB = AC,
∴∠B =∠C(等边对等角).
同理:∠C =∠A,
∴∠A =∠B =∠C(等量代换).
又∵∠A +∠B +∠C = 180°
∴∠A =∠B =∠C = 60°.
A
B
C
A
B
C
等边三角形的定义
三条边都相等的三角形叫做等边三角形(也叫正三角形).
等边三角形是特殊的等腰三角形.
有两边相等的三角形是等腰三角形(定义)
有两个角相等的三角形是等腰三角形.
满足什么条件的三角形是等边三角形?
满足什么条件的三角形是等腰三角形?
三边都相等的三角形是等边三角形(定义)
三个角都相等的三角形是等边三角形.
方法一:从边看
方法二:从角看
等边三角形有“三线合一”的性质吗?为什么?
结论:等边三角形每条边上的中线,高和所对角的平分线都三线合一。
A
B
C
如图,已知△ABC,△BDE都是等边三角形.
求证:AE=CD.
例5
例题讲解
∵△ABC和△BDE都是等边三角形,
∴AB=BC,BE=BD,∠ABC=∠DBE=60°.
在△ABE与△CBD中,
∴△ABE≌△CBD(SAS).
∴AE=CD.
证明:
1 已知AD是等边三角形ABC的高,且BD=1 cm,那么BC的长是( )
A.1 cm B.2 cm
C.3 cm D.4 cm
课堂练习
2 如图,等边三角形OAB的边长为2,则点B的坐标为( )
A.(1,1)
B.( ,1)
C.( , )
D.(1, )
3 如图,在△ABC中,AB=AC,下列条件中,不能使BD=CE的是( )
A.BD,CE为AC,AB边上的高
B.BD,CE都为△ABC的角平分线
C.∠ABD= ∠ABC,∠ACE= ∠ACB
D.∠ABD=∠BCE
4 下面关于等边三角形的说法正确的有( )
①三个角都相等;②三条边都相等;③是一种特殊的等腰三角形;④是一种特殊的直角三角形.
A.1个 B.2个
C.3个 D.4个
5 如图,在等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
A.45°
B.55°
C.60°
D.75°
变式提高
议一议:
已知:如图,在△ABC中,AB=AC,点D和点E分别在边AB和AC上.
(1)如果 ,那么BE=CD吗?
如果 呢?
由此你能得出什么结论呢?
结论:
在△ABC中,AB=AC,如果
那么BE=CD
变式提高
议一议:
已知:如图,在△ABC中,AB=AC,点D和点E分别在边AB和AC上.
(2)如果 ,那么BE=CD吗?
如果 呢?
由此你能得出什么结论呢?
在△ABC中,AB=AC,如果
那么BE=CD
结论:
回顾与思考
为什么等腰三角形有这样的特殊性质?一般三角形有类似的性质吗?
等腰三角形重要线段的结论:
等腰三角形两个底角的平分线_________;?
等腰三角形两腰上的高_________;?
等腰三角形两腰上的中线_________.?
归纳总结
相等
相等
相等
再见!!
等腰三角形2
复习回顾
我们学过的等腰三角形的性质有哪些?
边:
等腰三角形的两腰相等;
角:
等腰三角形的两底角相等;简述为:等边对等角.
重要线段:
等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合。简述为:“三线合一”
对称性:
等腰三角形是轴对称图形,对称轴只有一条,对称轴是顶角的平分线或底边上的中线或底边上的高所在的直线。
探究新知
你能画一个等腰三角形并作出它的两底角的平分线吗?
探究1:等腰三角形两底角的平分线有何关系?
做一做:
通过观察、测量,可猜想:等腰三角形两底角的平分线
_________.?你能尝试证明你猜想的结论吗?
探究新知
已知:如图,在△ABC中,AB=AC,CD和BE是△ABC的角平分线.
求证:CD=BE.
相等
证明:∵AB=AC,
∴∠ABC=∠ACB(等边对等角)
∵BE,CD为∠ABC,∠ACB的平分线,
∴∠3=∠4= ,∠1=∠2= .
∴∠4=∠1.
∠4=∠1, AC=AB,∠A=∠A.?
∴△ACD≌△ABE.
∴CD=BE?
在△ACD和△ABE中
结论:等腰三角形两底角的平分线相等。
探究2:等腰三角形两腰上的中线有何关系?
探究新知
已知:如图,在△ABC中,AB=AC,CD和BE是△ABC的中线.
求证:BE=CD.
相等
证明: ∵BE,CD为△ABC的中线,
∴AE= AD=
∵ AB=AC
∴AE=AD.
AB=AC,∠A=∠A,AE=AD.?
∴△ABE≌△ACD.
∴BE=CD?
在△ABE和△ACD中
结论:等腰三角形两腰上的中线相等。
探究3:等腰三角形两腰上的高线有何关系?
探究新知
已知:如图,在△ABC中,AB=AC,CD和BE是△ABC的高线.
求证:BE=CD.
相等
证明: ∵BE,CD为△ABC的高线,
∴
∴
∠AEB=∠ADC,∠A=∠A,AB=AC.?
∴△ABE≌△ACD.
∴BE=CD?
在△ABE和△ACD中
结论:等腰三角形两腰上的高线相等。
D
E
已知:如图,在△ABC 中, AB = AC,BD、CE 是△ABC 的高.
求证:BD = CE.
A
B
C
E
D
例 求证: 等腰三角形两腰上的高相等.
证明:∵ BD、CE 是△ABC 的高.
∴∠AEC =∠ADB = 90°.
在△ABD 和△ACE 中,
∵∠AEC =∠ADB = 90°,
AB = AC,∠A =∠A.
∴△ABD ≌△ACE(AAS).
∴BD = CE(全等三角形的对应边相等).
如图,在△ABC 中,AB = AC,点 D,E 分别在边 AC 和 AB 上.
议一议
E
D
A
B
C
(1)如果∠ABD = ∠ABC,∠ACE = ∠ACB,那么 BD = CE 吗?如果∠ABD = ∠ABC,∠ACE = ∠ACB 呢?由此你能得到一个什么结论?
1
3
1
3
1
4
1
4
E
D
A
B
C
BD = CE
(2)如果 AD = AC,AE = AB,那么 BD = CE 吗?如果 AD = AC,AE = AB 呢?由此你得到什么结论?
1
2
1
2
1
3
1
3
BD = CE
等腰三角形重要线段的结论:
等腰三角形两个底角的平分线_________;?
等腰三角形两腰上的高_________;?
等腰三角形两腰上的中线_________.?
归纳总结
相等
相等
相等
等边三角形的性质
知识点二
等边三角形的定义是什么?
想一想
等边三角形是特殊的等腰三角形,那么等边三角形的内角有什么特征呢?
定理 等边三角形的三个内角都相等,并且每个角都等于60°.
例 已知:如图,在△ABC 中,AB = BC = AC.
求证:∠A =∠B =∠C = 60°.
证明:∵AB = AC,
∴∠B =∠C(等边对等角).
同理:∠C =∠A,
∴∠A =∠B =∠C(等量代换).
又∵∠A +∠B +∠C = 180°
∴∠A =∠B =∠C = 60°.
A
B
C
A
B
C
等边三角形的定义
三条边都相等的三角形叫做等边三角形(也叫正三角形).
等边三角形是特殊的等腰三角形.
有两边相等的三角形是等腰三角形(定义)
有两个角相等的三角形是等腰三角形.
满足什么条件的三角形是等边三角形?
满足什么条件的三角形是等腰三角形?
三边都相等的三角形是等边三角形(定义)
三个角都相等的三角形是等边三角形.
方法一:从边看
方法二:从角看
等边三角形有“三线合一”的性质吗?为什么?
结论:等边三角形每条边上的中线,高和所对角的平分线都三线合一。
A
B
C
如图,已知△ABC,△BDE都是等边三角形.
求证:AE=CD.
例5
例题讲解
∵△ABC和△BDE都是等边三角形,
∴AB=BC,BE=BD,∠ABC=∠DBE=60°.
在△ABE与△CBD中,
∴△ABE≌△CBD(SAS).
∴AE=CD.
证明:
1 已知AD是等边三角形ABC的高,且BD=1 cm,那么BC的长是( )
A.1 cm B.2 cm
C.3 cm D.4 cm
课堂练习
2 如图,等边三角形OAB的边长为2,则点B的坐标为( )
A.(1,1)
B.( ,1)
C.( , )
D.(1, )
3 如图,在△ABC中,AB=AC,下列条件中,不能使BD=CE的是( )
A.BD,CE为AC,AB边上的高
B.BD,CE都为△ABC的角平分线
C.∠ABD= ∠ABC,∠ACE= ∠ACB
D.∠ABD=∠BCE
4 下面关于等边三角形的说法正确的有( )
①三个角都相等;②三条边都相等;③是一种特殊的等腰三角形;④是一种特殊的直角三角形.
A.1个 B.2个
C.3个 D.4个
5 如图,在等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
A.45°
B.55°
C.60°
D.75°
变式提高
议一议:
已知:如图,在△ABC中,AB=AC,点D和点E分别在边AB和AC上.
(1)如果 ,那么BE=CD吗?
如果 呢?
由此你能得出什么结论呢?
结论:
在△ABC中,AB=AC,如果
那么BE=CD
变式提高
议一议:
已知:如图,在△ABC中,AB=AC,点D和点E分别在边AB和AC上.
(2)如果 ,那么BE=CD吗?
如果 呢?
由此你能得出什么结论呢?
在△ABC中,AB=AC,如果
那么BE=CD
结论:
回顾与思考
为什么等腰三角形有这样的特殊性质?一般三角形有类似的性质吗?
等腰三角形重要线段的结论:
等腰三角形两个底角的平分线_________;?
等腰三角形两腰上的高_________;?
等腰三角形两腰上的中线_________.?
归纳总结
相等
相等
相等
再见!!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
