2020-2021学年九年级数学人教版下册 第27章:相似 精选提升练习(二) (Word版 含解析)
文档属性
| 名称 | 2020-2021学年九年级数学人教版下册 第27章:相似 精选提升练习(二) (Word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 137.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 00:00:00 | ||
图片预览



文档简介
2020-2021学年人教版九年级数学下册
第27章:相似
精选提升练习(二)
1.如图,在等腰Rt△ABC中,AC=BC,∠ACB=90°,点E在线段AB上,CF⊥CE,CF=CE,EF交AC于G,连接AF.
(1)填空:线段BE、AF的数量关系为
,位置关系为
;
(2)若当=时,求证:=2.
2.一块直角三角形木板的面积为1.5m2,一条直角边AB为1.5m,怎样才能把它加工成一个无拼接的面积最大的正方形桌面?甲、乙两位木匠的加工方法如图所示,请你用所学的知识说明哪位木匠的方法符合要求(加工损耗不计,计算结果中的分数可保留)
3.在边长为1的小正方形组成的网格中建立如图所示的平面直角坐标系,△ABC为格点三角形(顶点是网格线的交点).
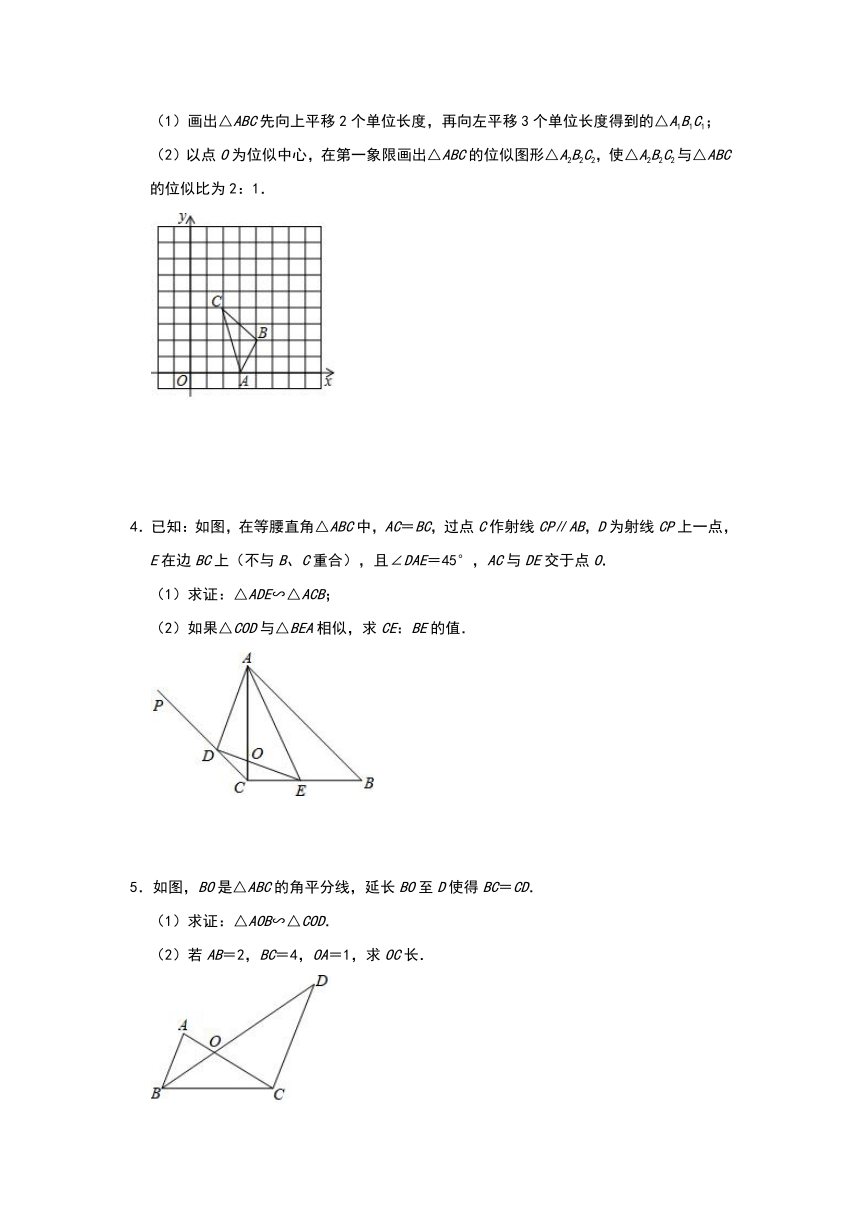
(1)画出△ABC先向上平移2个单位长度,再向左平移3个单位长度得到的△A1B1C1;
(2)以点O为位似中心,在第一象限画出△ABC的位似图形△A2B2C2,使△A2B2C2与△ABC的位似比为2:1.
4.已知:如图,在等腰直角△ABC中,AC=BC,过点C作射线CP∥AB,D为射线CP上一点,E在边BC上(不与B、C重合),且∠DAE=45°,AC与DE交于点O.
(1)求证:△ADE∽△ACB;
(2)如果△COD与△BEA相似,求CE:BE的值.
5.如图,BO是△ABC的角平分线,延长BO至D使得BC=CD.
(1)求证:△AOB∽△COD.
(2)若AB=2,BC=4,OA=1,求OC长.
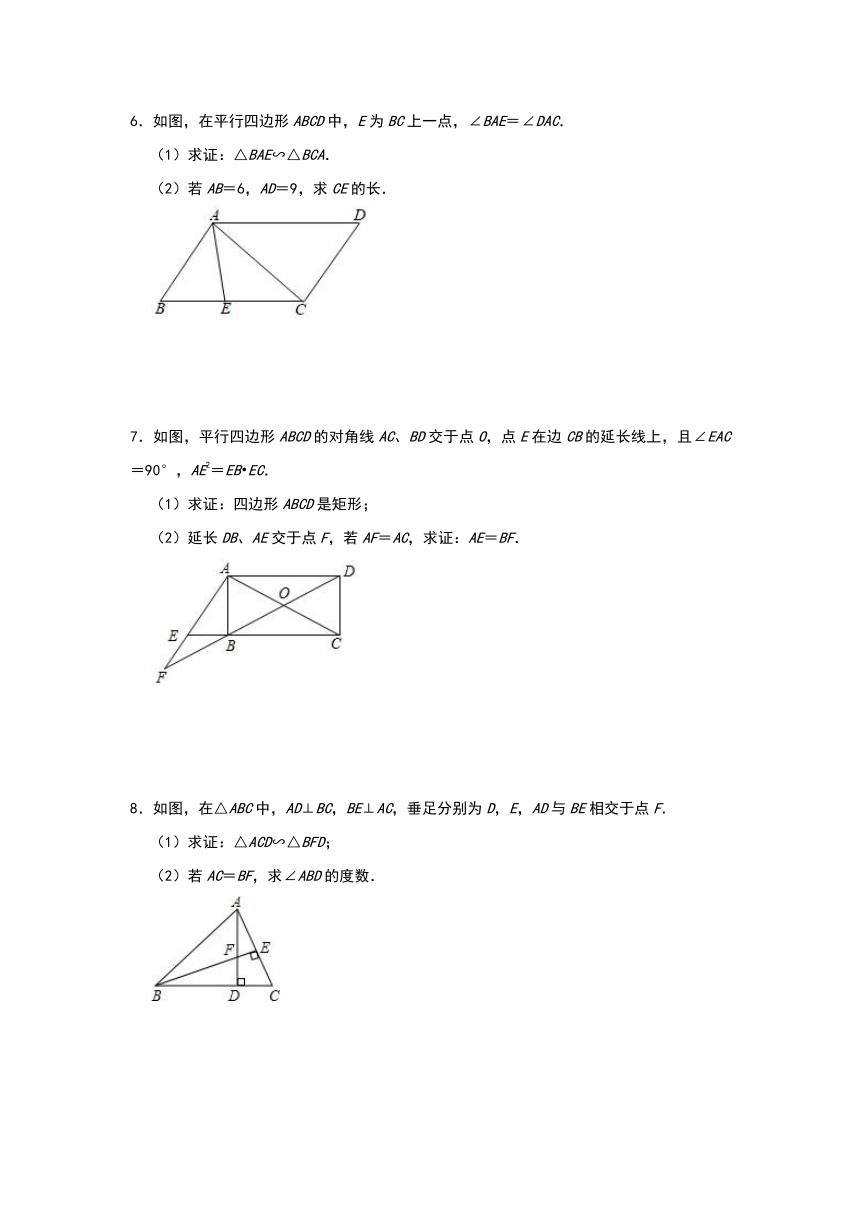
6.如图,在平行四边形ABCD中,E为BC上一点,∠BAE=∠DAC.
(1)求证:△BAE∽△BCA.
(2)若AB=6,AD=9,求CE的长.
7.如图,平行四边形ABCD的对角线AC、BD交于点O,点E在边CB的延长线上,且∠EAC=90°,AE2=EB?EC.
(1)求证:四边形ABCD是矩形;
(2)延长DB、AE交于点F,若AF=AC,求证:AE=BF.
8.如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
(1)求证:△ACD∽△BFD;
(2)若AC=BF,求∠ABD的度数.
9.在锐角△ABC中,边BC长为18,高AD长为12
(1)如图,矩形EFCH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K,求的值;
(2)设EH=x,矩形EFGH的面积为S,求S与x的函数关系式,并求S的最大值.
10.如图所示,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm,点P由点B出发沿BA方向向点A匀速运动,同时点Q由点A出发沿AC方向向点C匀速运动,它们的速度均为1cm/s.连接PQ,设运动时间为t(s)(0<t<4).
(1)当t为何值时,PQ⊥AC?
(2)设△APQ的面积为S,求S与t的函数关系式,并求出当t为何值时,S取得最大值?S的最大值是多少?
参考答案
1.(1)解:∵CF⊥CE,∠ACB=90°,
∴∠FCA+∠ACE=∠ACE+∠BCE=90°,
∴∠FCA=∠ECB,
在△ACF和△BCE中,
,
∴△ACF≌△BCE(SAS),
∴BE=AF,∠FAC=∠EBC,
∵∠EBC+∠CAE=90°,
∴∠FAC+∠CAE=90°
(2)证明:作GM⊥AB于M,GN⊥AF于N,
∵△ACF可由△BCE绕点C顺时针方向旋转90°而得到,
∴AF=BE,∠CAF=∠CBE=45°.
∴AE=2AF,∠CAF=∠CAB,
∴GM=GN.
∴S△AEG=2S△AFG,
∴EG=2GF,
∴=2.
2.解:由AB=1.5m,S△ABC=1.5m2,可得BC=2m,
由图甲,过点B作Rt△ABC斜边AC上的高,BH交DE于P,交AC于H.
由AB=1.5m,BC=2m,
得AC==2.5(m),
由AC?BH=AB?BC
可得:BH==1.2(m),
设甲设计的桌面的边长为xm,
∵DE∥AC,
∴Rt△BDE∽Rt△BAC,
∴=,即=,
解得x=(m),
由图乙,若设乙设计的正方形桌面边长为ym,
由DE∥AB,得Rt△CDE∽Rt△CBA,
∴=,即=,
解得y=(m),
∵x=,y=,
∴x<y,即x2<y2,
∴S正方形甲<S正方形乙,
∴第二个正方形面积大
3.解:(1)△A1B1C1;如图所示.
(2)△A2B2C2如图所示.
4.(1)证明:由题意可知∠CAD+∠CAE=∠CAE+∠BAE=45°,
∴∠CAD=∠BAE;
∵CP∥AB,
∴∠ACD=∠CAB=45°.
∴△ACD∽△ABE,
∴=,即=,
又∵∠DAE=∠CAB=45°,
∴△ADE∽△ACB.
(2)解:在△COD与△BEA中,∠DCO=∠B=45°,∠DOC与∠AEB均为钝角,
∴如果△COD与△BEA相似,只能是△COD∽△BEA,
∴∠1=∠2.
∵∠AEC=∠AED+∠3=45°+∠3,∠AEC=∠B+∠2=45°+∠2,
∴∠3=∠2,
∴∠1=∠2=∠3,
∴CE=CD.
∵CP∥AB,
∴∠DCE+∠B=180°,
∴∠DCE=180°﹣∠B=135°,
∴∠1=∠2=∠3=(180°﹣∠DCE)=22.5°,
∴∠2=∠CAB,即AE为角平分线.
如答图2,过点E作EG⊥AB于点G,则EG=CE,且△BEG为等腰直角三角形.
∴EG=BG=CE=CD,BE=EG,
∴CE:BE=.
5.解:(1)∵BO是△ABC的角平分线,
∴∠ABO=∠CBO,
∵BC=CD,
∴∠CBO=∠D,
∴∠ABO=∠D,
又∵∠AOB=∠COD,
∴△AOB∽△COD;
(2)∵BC=4,
∴BC=CD=4,
∵△AOB∽△COD,
∴=,即=,
解得:OC=2.
6.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠ACB,
∵∠BAE=∠DAC,
∴∠BAE=∠ACB,
∵∠B=∠B,
∴△BAE∽△BCA;
(2)解:∵四边形ABCD是平行四边形,
∴AD=BC=9,
由(1)知,△BAE∽△BCA,
∴,
∴BA2=BE?BC,
∴BE===4,
∴CE=BC﹣BE=9﹣4=5.
7.证明:(1)∵AE2=EB?EC
∴
又∵∠AEB=∠CEA
∴△AEB∽△CEA
∴∠EBA=∠EAC
而∠EAC=90°
∴∠EBA=∠EAC=90°
又∵∠EBA+∠CBA=180°
∴∠CBA=90°
而四边形ABCD是平行四边形
∴四边形ABCD是矩形
即得证.
(2)∵△AEB∽△CEA
∴即,∠EAB=∠ECA
∵四边形ABCD是矩形
∴OB=OC
∴∠OBC=∠ECA
∴∠EBF=∠OBC=∠ECA=∠EAB
即∠EBF=∠EAB
又∵∠F=∠F
∴△EBF∽△BAF
∴
∴
而AF=AC
∴BF=AE
即AE=BF得证.
8.(1)证明:∵AD⊥BC,BE⊥AC,
∴∠DAC+∠C=90°,∠FBD+∠C=90°,
∴∠DAC=∠FBD,又∠BDF=∠ADC=90°,
∴△ACD∽△BFD;
(2)解:∵△ACD∽△BFD,AC=BF,
∴△ACD≌△BFD,
∴DA=DB,又AD⊥BC,
∴∠ABD=45°.
9.解:(1)∵△AEF∽△ABC,
∴=,
∵边BC长为18,高AD长为12,
∴==;
(2)∵EH=KD=x,
∴AK=12﹣x,EF=(12﹣x),
∴S=x(12﹣x)=﹣(x﹣6)2+54,
当x=6时,S有最大值为54.
10.解:(1)∵PQ⊥AC,
∴∠AQP=∠C=90°,
∴PQ∥BC,
∴=,
在Rt△ACB中,AB===5,
∴=,
解得t=,
∴t为时,PQ⊥AC.
(2)如图,作PH⊥AC于H.
∵PH∥BC,
∴=,
∴=,
∴PH=(5﹣t),
∴S=?AQ?PH=?t?(5﹣t)=﹣t2+t=﹣(t﹣)2+,
∵﹣<0,
∴t=,S有最大值,最大值为.
第27章:相似
精选提升练习(二)
1.如图,在等腰Rt△ABC中,AC=BC,∠ACB=90°,点E在线段AB上,CF⊥CE,CF=CE,EF交AC于G,连接AF.
(1)填空:线段BE、AF的数量关系为
,位置关系为
;
(2)若当=时,求证:=2.
2.一块直角三角形木板的面积为1.5m2,一条直角边AB为1.5m,怎样才能把它加工成一个无拼接的面积最大的正方形桌面?甲、乙两位木匠的加工方法如图所示,请你用所学的知识说明哪位木匠的方法符合要求(加工损耗不计,计算结果中的分数可保留)
3.在边长为1的小正方形组成的网格中建立如图所示的平面直角坐标系,△ABC为格点三角形(顶点是网格线的交点).
(1)画出△ABC先向上平移2个单位长度,再向左平移3个单位长度得到的△A1B1C1;
(2)以点O为位似中心,在第一象限画出△ABC的位似图形△A2B2C2,使△A2B2C2与△ABC的位似比为2:1.
4.已知:如图,在等腰直角△ABC中,AC=BC,过点C作射线CP∥AB,D为射线CP上一点,E在边BC上(不与B、C重合),且∠DAE=45°,AC与DE交于点O.
(1)求证:△ADE∽△ACB;
(2)如果△COD与△BEA相似,求CE:BE的值.
5.如图,BO是△ABC的角平分线,延长BO至D使得BC=CD.
(1)求证:△AOB∽△COD.
(2)若AB=2,BC=4,OA=1,求OC长.
6.如图,在平行四边形ABCD中,E为BC上一点,∠BAE=∠DAC.
(1)求证:△BAE∽△BCA.
(2)若AB=6,AD=9,求CE的长.
7.如图,平行四边形ABCD的对角线AC、BD交于点O,点E在边CB的延长线上,且∠EAC=90°,AE2=EB?EC.
(1)求证:四边形ABCD是矩形;
(2)延长DB、AE交于点F,若AF=AC,求证:AE=BF.
8.如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
(1)求证:△ACD∽△BFD;
(2)若AC=BF,求∠ABD的度数.
9.在锐角△ABC中,边BC长为18,高AD长为12
(1)如图,矩形EFCH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K,求的值;
(2)设EH=x,矩形EFGH的面积为S,求S与x的函数关系式,并求S的最大值.
10.如图所示,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm,点P由点B出发沿BA方向向点A匀速运动,同时点Q由点A出发沿AC方向向点C匀速运动,它们的速度均为1cm/s.连接PQ,设运动时间为t(s)(0<t<4).
(1)当t为何值时,PQ⊥AC?
(2)设△APQ的面积为S,求S与t的函数关系式,并求出当t为何值时,S取得最大值?S的最大值是多少?
参考答案
1.(1)解:∵CF⊥CE,∠ACB=90°,
∴∠FCA+∠ACE=∠ACE+∠BCE=90°,
∴∠FCA=∠ECB,
在△ACF和△BCE中,
,
∴△ACF≌△BCE(SAS),
∴BE=AF,∠FAC=∠EBC,
∵∠EBC+∠CAE=90°,
∴∠FAC+∠CAE=90°
(2)证明:作GM⊥AB于M,GN⊥AF于N,
∵△ACF可由△BCE绕点C顺时针方向旋转90°而得到,
∴AF=BE,∠CAF=∠CBE=45°.
∴AE=2AF,∠CAF=∠CAB,
∴GM=GN.
∴S△AEG=2S△AFG,
∴EG=2GF,
∴=2.
2.解:由AB=1.5m,S△ABC=1.5m2,可得BC=2m,
由图甲,过点B作Rt△ABC斜边AC上的高,BH交DE于P,交AC于H.
由AB=1.5m,BC=2m,
得AC==2.5(m),
由AC?BH=AB?BC
可得:BH==1.2(m),
设甲设计的桌面的边长为xm,
∵DE∥AC,
∴Rt△BDE∽Rt△BAC,
∴=,即=,
解得x=(m),
由图乙,若设乙设计的正方形桌面边长为ym,
由DE∥AB,得Rt△CDE∽Rt△CBA,
∴=,即=,
解得y=(m),
∵x=,y=,
∴x<y,即x2<y2,
∴S正方形甲<S正方形乙,
∴第二个正方形面积大
3.解:(1)△A1B1C1;如图所示.
(2)△A2B2C2如图所示.
4.(1)证明:由题意可知∠CAD+∠CAE=∠CAE+∠BAE=45°,
∴∠CAD=∠BAE;
∵CP∥AB,
∴∠ACD=∠CAB=45°.
∴△ACD∽△ABE,
∴=,即=,
又∵∠DAE=∠CAB=45°,
∴△ADE∽△ACB.
(2)解:在△COD与△BEA中,∠DCO=∠B=45°,∠DOC与∠AEB均为钝角,
∴如果△COD与△BEA相似,只能是△COD∽△BEA,
∴∠1=∠2.
∵∠AEC=∠AED+∠3=45°+∠3,∠AEC=∠B+∠2=45°+∠2,
∴∠3=∠2,
∴∠1=∠2=∠3,
∴CE=CD.
∵CP∥AB,
∴∠DCE+∠B=180°,
∴∠DCE=180°﹣∠B=135°,
∴∠1=∠2=∠3=(180°﹣∠DCE)=22.5°,
∴∠2=∠CAB,即AE为角平分线.
如答图2,过点E作EG⊥AB于点G,则EG=CE,且△BEG为等腰直角三角形.
∴EG=BG=CE=CD,BE=EG,
∴CE:BE=.
5.解:(1)∵BO是△ABC的角平分线,
∴∠ABO=∠CBO,
∵BC=CD,
∴∠CBO=∠D,
∴∠ABO=∠D,
又∵∠AOB=∠COD,
∴△AOB∽△COD;
(2)∵BC=4,
∴BC=CD=4,
∵△AOB∽△COD,
∴=,即=,
解得:OC=2.
6.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠ACB,
∵∠BAE=∠DAC,
∴∠BAE=∠ACB,
∵∠B=∠B,
∴△BAE∽△BCA;
(2)解:∵四边形ABCD是平行四边形,
∴AD=BC=9,
由(1)知,△BAE∽△BCA,
∴,
∴BA2=BE?BC,
∴BE===4,
∴CE=BC﹣BE=9﹣4=5.
7.证明:(1)∵AE2=EB?EC
∴
又∵∠AEB=∠CEA
∴△AEB∽△CEA
∴∠EBA=∠EAC
而∠EAC=90°
∴∠EBA=∠EAC=90°
又∵∠EBA+∠CBA=180°
∴∠CBA=90°
而四边形ABCD是平行四边形
∴四边形ABCD是矩形
即得证.
(2)∵△AEB∽△CEA
∴即,∠EAB=∠ECA
∵四边形ABCD是矩形
∴OB=OC
∴∠OBC=∠ECA
∴∠EBF=∠OBC=∠ECA=∠EAB
即∠EBF=∠EAB
又∵∠F=∠F
∴△EBF∽△BAF
∴
∴
而AF=AC
∴BF=AE
即AE=BF得证.
8.(1)证明:∵AD⊥BC,BE⊥AC,
∴∠DAC+∠C=90°,∠FBD+∠C=90°,
∴∠DAC=∠FBD,又∠BDF=∠ADC=90°,
∴△ACD∽△BFD;
(2)解:∵△ACD∽△BFD,AC=BF,
∴△ACD≌△BFD,
∴DA=DB,又AD⊥BC,
∴∠ABD=45°.
9.解:(1)∵△AEF∽△ABC,
∴=,
∵边BC长为18,高AD长为12,
∴==;
(2)∵EH=KD=x,
∴AK=12﹣x,EF=(12﹣x),
∴S=x(12﹣x)=﹣(x﹣6)2+54,
当x=6时,S有最大值为54.
10.解:(1)∵PQ⊥AC,
∴∠AQP=∠C=90°,
∴PQ∥BC,
∴=,
在Rt△ACB中,AB===5,
∴=,
解得t=,
∴t为时,PQ⊥AC.
(2)如图,作PH⊥AC于H.
∵PH∥BC,
∴=,
∴=,
∴PH=(5﹣t),
∴S=?AQ?PH=?t?(5﹣t)=﹣t2+t=﹣(t﹣)2+,
∵﹣<0,
∴t=,S有最大值,最大值为.
