(课件)第三章《证明(一)》复习
图片预览



文档简介
(共24张PPT)
义务教育课程标准实验教科书
八年级 上 册
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8
0 1 2 3 4 5
0 1 2 3 4 5
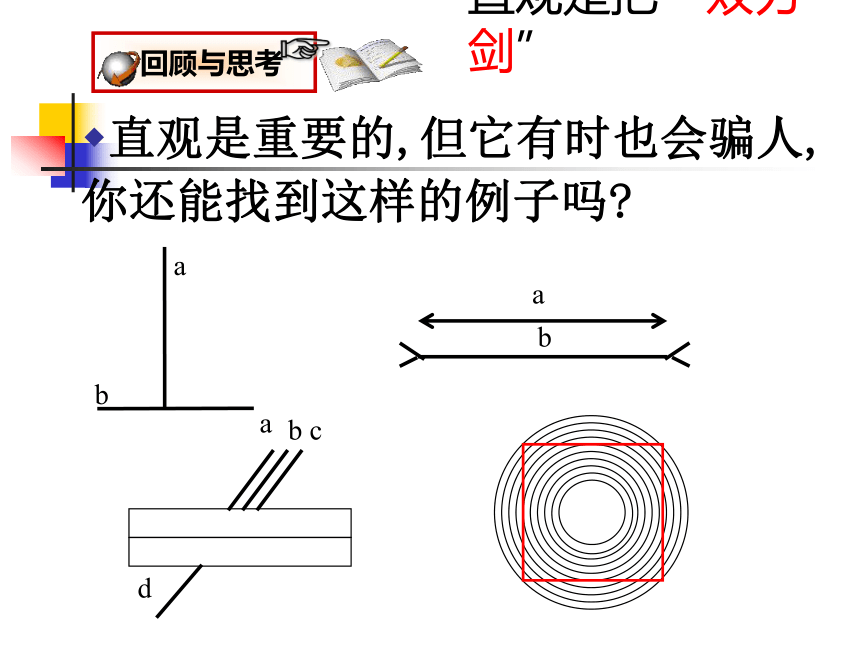
回顾与思考
直观是把“双刃剑”
直观是重要的,但它有时也会骗人,你还能找到这样的例子吗
回顾与思考
a
b
c
d
a
b
a
b
每个命题都由条件和结论两部分组成.条件是已知事项,结论是由已知项推断出的事项.
一般地,命题可以写成“如果……,那么……”的形式,其中“如果”引出的部分是条件,“那么”引出的部分是结论.
正确的命题称为真命题,不正确的的命题称为假命题
要说明一个命题是假命题,通常可以举出一个例子,使之具备命题的条件,而不具备命题的结论,这种例子称为反例.
定义:对名称和术语的含义加以描述,作出明确
的规定,也就是给出它们的定义.
命题:判断一件事情的句子,叫做命题.
回顾与思考
知多少
公理:公认的真命题称为公理(axiom).
证明:除了公理外,其它真命题的正确性都通过推理
的方法证实.推理的过程称为证明.
定理:经过证明的真命题称为定理(theorem).
本套教材选用如下命题作为公理 :
1.两直线被第三条直线所截,如果同位角相等,
那么这两条直线平行;
2.两条平行线被第三条直线所截,同位角相等;
3.两边夹角对应相等的两个三角形全等;
4.两角及其夹边对应相等的两个三角形全等;
5.三边对应相等的两个三角形全等;
6.全等三角形的对应边相等,对应角相等.
回顾与思考
知多少
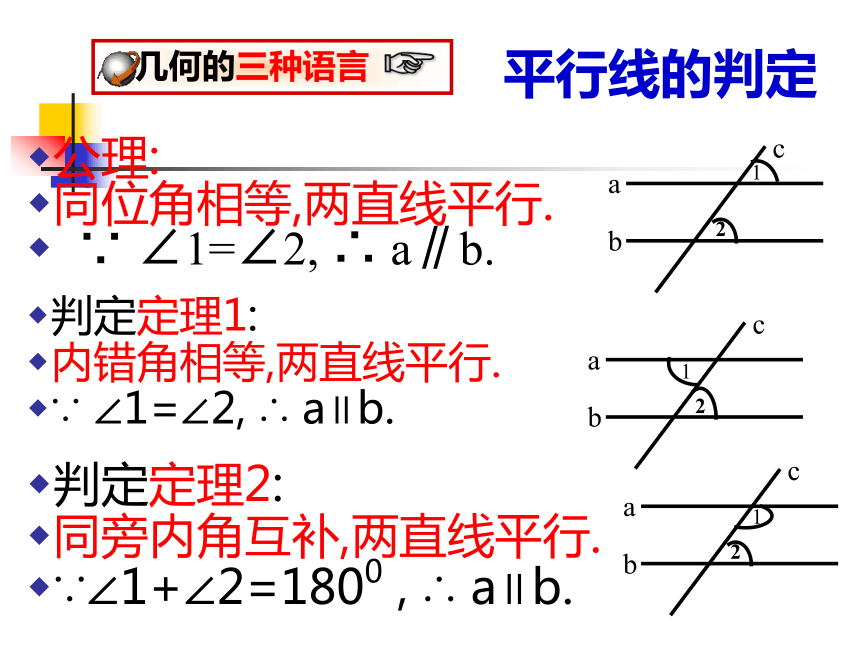
平行线的判定
公理:
同位角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.
判定定理1:
内错角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.
判定定理2:
同旁内角互补,两直线平行.
∵∠1+∠2=1800 , ∴ a∥b.
a
b
c
2
1
a
b
c
1
2
a
b
c
1
2
几何的三种语言
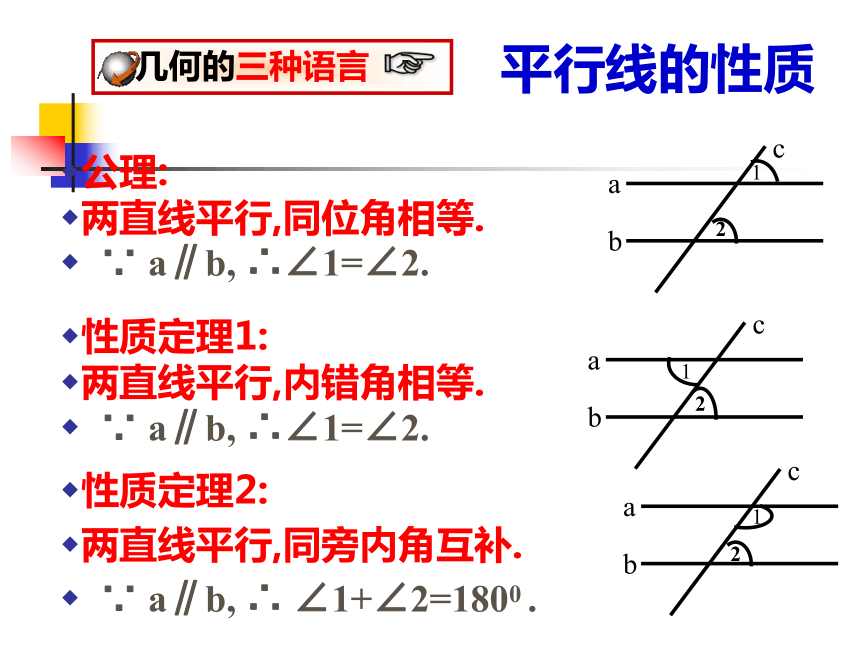
公理:
两直线平行,同位角相等.
∵ a∥b, ∴∠1=∠2.
性质定理1:
两直线平行,内错角相等.
∵ a∥b, ∴∠1=∠2.
性质定理2:
两直线平行,同旁内角互补.
∵ a∥b, ∴ ∠1+∠2=1800 .
a
b
c
2
1
a
b
c
1
2
a
b
c
1
2
几何的三种语言
平行线的性质
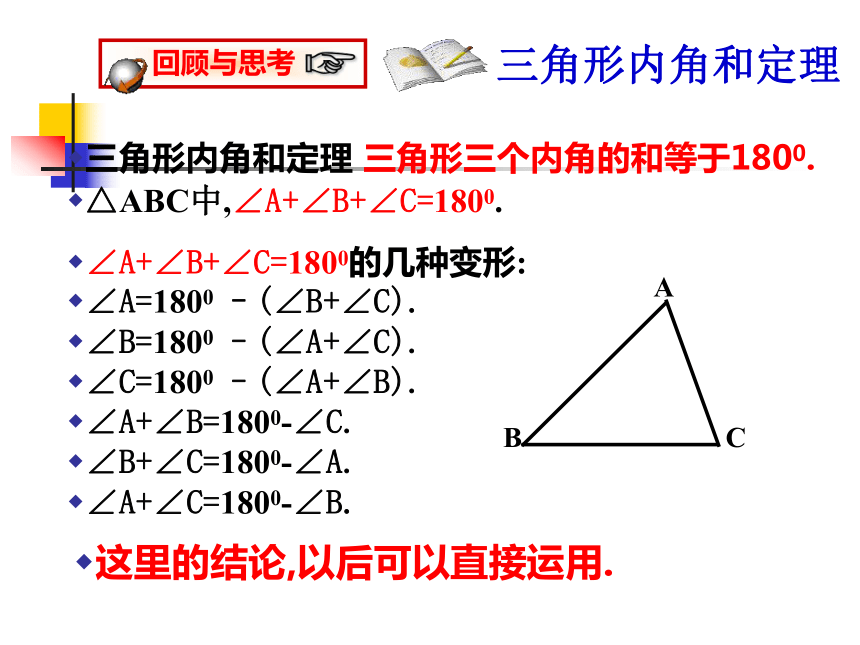
三角形内角和定理
三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.
∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.
这里的结论,以后可以直接运用.
A
B
C
回顾与思考
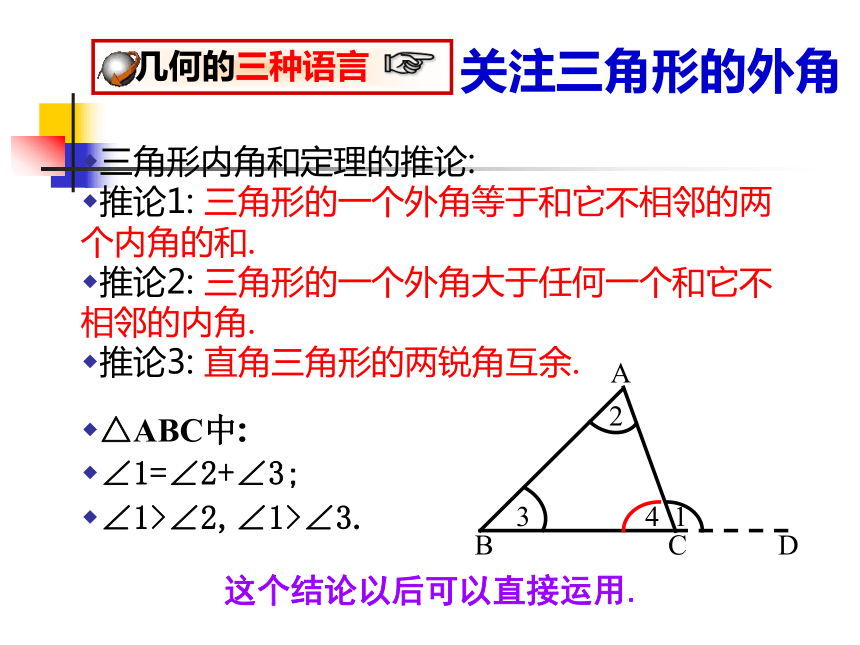
关注三角形的外角
三角形内角和定理的推论:
推论1: 三角形的一个外角等于和它不相邻的两个内角的和.
推论2: 三角形的一个外角大于任何一个和它不相邻的内角.
推论3: 直角三角形的两锐角互余.
△ABC中:
∠1=∠2+∠3;
∠1>∠2,∠1>∠3.
A
B
C
D
1
2
3
4
这个结论以后可以直接运用.
几何的三种语言
证明一个命题的一般步骤:
(1)弄清题设和结论;
(2)根据题意画出相应的图形;
(3)根据题设和结论写出已知,求证;
(4)分析证明思路,写出证明过程.
胜者的“钥匙”
回顾与思考
“行家”看“门道”
如图:∠1是△ABC的一个外角, ∠1与图中的
其它角有什么关系
∠1+∠4=1800 ;
∠1>∠2;
∠1>∠3;
∠1=∠2+∠3.
证明:∵∠2+∠3+∠4=1800(三角形内角和定理),
∠1+∠4=1800(平角的意义),
∴∠1= ∠2+∠3.(等量代换).
∴ ∠1>∠2,∠1>∠3(和大于部分).
探索思考
A
B
C
D
1
2
3
4
能证明你的结论吗
用文字表述为:
三角形的一个外角等于和它不相邻的两个内角的和.
三角形的一个外角大于任何一个和它不相邻的内角.
内涵与外延
在这里,我们通过三角形内角和定理直接推导出两个新定理.像这样,由一个公理或定理直接推出的定理,叫做这个公理或定理的推论.
推论可以当作定理使用.
三角形内角和定理的推论:
推论1: 三角形的一个外角等于和它不相邻的两个内角的和.
推论2: 三角形的一个外角大于任何一个和它不相邻的内角.
关注▲外角
A
B
C
D
1
2
3
4
“行家”看“门道”
例1 已知:如图,在△ABC中,AD平分外角
∠EAC,∠B= ∠C.
求证:AD∥BC.
证明: ∵ ∠EAC=∠B+∠C (三角形的一个外角等于和它不相邻的两个内角的和),
例题欣赏
∴ a∥b(内错角相等,两直线平行).
∠B=∠C (已知),
∴∠DAC=∠C(等量代换).
A
C
D
B
E
分析:要证明AD∥BC,只需要证明“同位角相等”,“内错角相等”或“同旁内角互补”.
∵ AD平分 ∠EAC(已知).
∴ ∠C= ∠EAC(等式性质).
∴∠DAC= ∠EAC(角平分线的定义).
·
·
例题是运用了定理“内错角相等,两直线平行”得到了证实.
例2 已知:如图,在△ABC中, ∠1是它的一个外角, E为边AC上一点,延长BC到D,连接DE.
求证: ∠1>∠2.
证明:∵ ∠1是△ABC的一个外角(已知),
把你所悟到的证明一个真命题的方法,步骤,书写格式以及注意事项内化为一种方法.
∴ ∠1>∠3(三角形的一个外角大于
任何一个和 它不相邻的内角).
∵∠3是△CDE的一个外角 (外角定义).
∴∠3>∠2(三角形的一个外角大于任
何一个和 它不相邻的内角).
∴ ∠1>∠2(不等式的性质).
C
A
B
F
1
3
4
5
E
D
2
例题欣赏
“行家”看“门道”
我能行
已知:如图所示,在△ABC中,外角∠DCA=100°,
∠A=45°.
求:∠B和∠ACB的大小.
A
B
C
D
解:
∵ ∠DCA是△ABC的一个外角(已知)
∠DCA=100°(已知),
∴ ∠B=100°-45°=55°.(三角形的一个外角等
于和它不相邻的两个内角的和).
又∵ ∠DCA+∠BCA=180°(平角意义).
∴ ∠ACB=80°(等式的性质).
∠A=45°(已知),
例题欣赏
你认识外角吗
已知:国旗上的正五角星形如图所示.
求:∠A+∠B+∠C+∠D+∠E的度数.
解:∵∠1是△BDF的一个外角(外角的意义)
分析:设法利用外角把这五个角“凑”到一个三角形中,运用三角形内角和定理来求解.
∴ ∠1=∠B+∠D(三角形的一个外角等于
和它不相邻的两个内角的和)
∴ ∠2=∠C+∠E(三角形的一个外角等于和它不相邻的两个内角的和)
又∵∠A+∠1+∠2=180°(三角形内角和定理)
又∵ ∠2是△EHC的一个外角(外角的意义)
A
B
C
D
E
F
1
H
2
∴ ∠A+∠B+∠C+∠D+∠E =180°(等式性质)
例题欣赏
你认识外角吗
试一试
证明(1):∵ ∠BDC是△DCE的一个外角 (外角意义),
∴ ∠BDC>∠CED(三角形的一个外角大于和它不相邻的任何一个外角).
∴ ∠DEC>∠A(三角形的一个外角大于和它不相邻的任何一个外角).
∴ ∠BDC>∠A (不等式的性质).
∵ ∠DEC是△ABE的一个外角 (外角意义),
已知: 如图所示.
求证: (1)∠BDC>∠A;
(2) ∠BDC=∠A+∠B+∠C.
B
C
A
D
E
你认识外角吗
已知: 如图所示.
求证: (1)∠BDC>∠A;
(2) ∠BDC=∠A+∠B+∠C.
试一试
证明(2):∵ ∠BDC是△DCE的一个外角 (外角意义),
∴ ∠BDC =∠C+∠CED(三角形的一个外角等于和它不相邻的两个内角的和).
∴ ∠DEC=∠A+ ∠B(三角形的一个外角等于和它不相邻的两个外角的和).
∴ ∠BDC=∠A+∠B+∠C (等式的性质).
∵ ∠DEC是△ABE的一个外角 (外角意义),
B
C
A
D
E
回味无穷
理解几何命题证明的方法,步骤,格式及注意事项.
三角形内角和定理
三角形三个内角的和等于1800.△ABC中,
∠A+∠B+∠C=1800.
推论1: 三角形的一个外角等于和它不相邻的两个内角的和.
推论2: 三角形的一个外角大于任何一个和它不相邻的内角.
关注三角形的外角.
推论3: 直角三角形的两锐角互余.
你准备如何提高证明命题的能力呢
小结 拓展
1.如图:将正方形的四个顶点用线段连接,什么样的线段最短?研究发现,并非对角线最短,而是如图所示的连法最短(即用线段AE,DE,EF,BF,CF把四个顶点连接起来) .
已知图中∠DAE=∠ADE=300,∠AEF=∠BFE=1200 .
你能证明此时的AB∥EF吗?.
证明:∵∠DAB=900(正方形性质) ,∠DAE=300(已知),
∴∠BAE=600(等式性质).
∵∠AEF=1200(已知),
∴∠BAE+∠AEF=1800(等式性质) .
∴ AB∥EF(同旁内角相等,两直线平行).
A
B
C
D
1题图
E
F
“行家”看“门道”
∴∠2+∠4=1800 ( 两直线平行,同旁内角互补)
2.已知:如图,直线 a,b被 直线c所截,a∥b.
求证:∠1+∠2=1800.
b
a
c
2
1
2题图
证明1:∵ a∥b(已知)
∴∠2=∠3 (两直线平行,内错角相等)
3
又∵∠1+∠3= 1800 (平角意义)
∴∠1+∠2= 1800 (等量代换)
证明2:∵ a∥b(已知)
∠1=∠4 ( 对顶角相等)
∴∠1+∠2= 1800 (等量代换).
4
“行家”看“门道”
3.已知:如图,∠1+∠2=1800.
求证: ∠3=∠4.
分析:要证明∠3=∠4,只要证明CD∥EF ;而由∠1+∠2=1800,可得∠1+∠5=1800.从而可得CD∥EF
4
1
2
3
O
C
E
A
B
F
D
3题图
证明:∵ ∠1+∠2=1800 (已知) ,
5
∠5=∠2(对顶角相等),
∴∠1+∠5=1800 (等量代换).
∴ CD∥EF (同旁内角互补,两直线平行).
∴∠3=∠4(两直线平行,同位角相等).
“行家”看“门道”
知识的升华
作业:复习题
义务教育课程标准实验教科书
八年级 上 册
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8
0 1 2 3 4 5
0 1 2 3 4 5
回顾与思考
直观是把“双刃剑”
直观是重要的,但它有时也会骗人,你还能找到这样的例子吗
回顾与思考
a
b
c
d
a
b
a
b
每个命题都由条件和结论两部分组成.条件是已知事项,结论是由已知项推断出的事项.
一般地,命题可以写成“如果……,那么……”的形式,其中“如果”引出的部分是条件,“那么”引出的部分是结论.
正确的命题称为真命题,不正确的的命题称为假命题
要说明一个命题是假命题,通常可以举出一个例子,使之具备命题的条件,而不具备命题的结论,这种例子称为反例.
定义:对名称和术语的含义加以描述,作出明确
的规定,也就是给出它们的定义.
命题:判断一件事情的句子,叫做命题.
回顾与思考
知多少
公理:公认的真命题称为公理(axiom).
证明:除了公理外,其它真命题的正确性都通过推理
的方法证实.推理的过程称为证明.
定理:经过证明的真命题称为定理(theorem).
本套教材选用如下命题作为公理 :
1.两直线被第三条直线所截,如果同位角相等,
那么这两条直线平行;
2.两条平行线被第三条直线所截,同位角相等;
3.两边夹角对应相等的两个三角形全等;
4.两角及其夹边对应相等的两个三角形全等;
5.三边对应相等的两个三角形全等;
6.全等三角形的对应边相等,对应角相等.
回顾与思考
知多少
平行线的判定
公理:
同位角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.
判定定理1:
内错角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.
判定定理2:
同旁内角互补,两直线平行.
∵∠1+∠2=1800 , ∴ a∥b.
a
b
c
2
1
a
b
c
1
2
a
b
c
1
2
几何的三种语言
公理:
两直线平行,同位角相等.
∵ a∥b, ∴∠1=∠2.
性质定理1:
两直线平行,内错角相等.
∵ a∥b, ∴∠1=∠2.
性质定理2:
两直线平行,同旁内角互补.
∵ a∥b, ∴ ∠1+∠2=1800 .
a
b
c
2
1
a
b
c
1
2
a
b
c
1
2
几何的三种语言
平行线的性质
三角形内角和定理
三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.
∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.
这里的结论,以后可以直接运用.
A
B
C
回顾与思考
关注三角形的外角
三角形内角和定理的推论:
推论1: 三角形的一个外角等于和它不相邻的两个内角的和.
推论2: 三角形的一个外角大于任何一个和它不相邻的内角.
推论3: 直角三角形的两锐角互余.
△ABC中:
∠1=∠2+∠3;
∠1>∠2,∠1>∠3.
A
B
C
D
1
2
3
4
这个结论以后可以直接运用.
几何的三种语言
证明一个命题的一般步骤:
(1)弄清题设和结论;
(2)根据题意画出相应的图形;
(3)根据题设和结论写出已知,求证;
(4)分析证明思路,写出证明过程.
胜者的“钥匙”
回顾与思考
“行家”看“门道”
如图:∠1是△ABC的一个外角, ∠1与图中的
其它角有什么关系
∠1+∠4=1800 ;
∠1>∠2;
∠1>∠3;
∠1=∠2+∠3.
证明:∵∠2+∠3+∠4=1800(三角形内角和定理),
∠1+∠4=1800(平角的意义),
∴∠1= ∠2+∠3.(等量代换).
∴ ∠1>∠2,∠1>∠3(和大于部分).
探索思考
A
B
C
D
1
2
3
4
能证明你的结论吗
用文字表述为:
三角形的一个外角等于和它不相邻的两个内角的和.
三角形的一个外角大于任何一个和它不相邻的内角.
内涵与外延
在这里,我们通过三角形内角和定理直接推导出两个新定理.像这样,由一个公理或定理直接推出的定理,叫做这个公理或定理的推论.
推论可以当作定理使用.
三角形内角和定理的推论:
推论1: 三角形的一个外角等于和它不相邻的两个内角的和.
推论2: 三角形的一个外角大于任何一个和它不相邻的内角.
关注▲外角
A
B
C
D
1
2
3
4
“行家”看“门道”
例1 已知:如图,在△ABC中,AD平分外角
∠EAC,∠B= ∠C.
求证:AD∥BC.
证明: ∵ ∠EAC=∠B+∠C (三角形的一个外角等于和它不相邻的两个内角的和),
例题欣赏
∴ a∥b(内错角相等,两直线平行).
∠B=∠C (已知),
∴∠DAC=∠C(等量代换).
A
C
D
B
E
分析:要证明AD∥BC,只需要证明“同位角相等”,“内错角相等”或“同旁内角互补”.
∵ AD平分 ∠EAC(已知).
∴ ∠C= ∠EAC(等式性质).
∴∠DAC= ∠EAC(角平分线的定义).
·
·
例题是运用了定理“内错角相等,两直线平行”得到了证实.
例2 已知:如图,在△ABC中, ∠1是它的一个外角, E为边AC上一点,延长BC到D,连接DE.
求证: ∠1>∠2.
证明:∵ ∠1是△ABC的一个外角(已知),
把你所悟到的证明一个真命题的方法,步骤,书写格式以及注意事项内化为一种方法.
∴ ∠1>∠3(三角形的一个外角大于
任何一个和 它不相邻的内角).
∵∠3是△CDE的一个外角 (外角定义).
∴∠3>∠2(三角形的一个外角大于任
何一个和 它不相邻的内角).
∴ ∠1>∠2(不等式的性质).
C
A
B
F
1
3
4
5
E
D
2
例题欣赏
“行家”看“门道”
我能行
已知:如图所示,在△ABC中,外角∠DCA=100°,
∠A=45°.
求:∠B和∠ACB的大小.
A
B
C
D
解:
∵ ∠DCA是△ABC的一个外角(已知)
∠DCA=100°(已知),
∴ ∠B=100°-45°=55°.(三角形的一个外角等
于和它不相邻的两个内角的和).
又∵ ∠DCA+∠BCA=180°(平角意义).
∴ ∠ACB=80°(等式的性质).
∠A=45°(已知),
例题欣赏
你认识外角吗
已知:国旗上的正五角星形如图所示.
求:∠A+∠B+∠C+∠D+∠E的度数.
解:∵∠1是△BDF的一个外角(外角的意义)
分析:设法利用外角把这五个角“凑”到一个三角形中,运用三角形内角和定理来求解.
∴ ∠1=∠B+∠D(三角形的一个外角等于
和它不相邻的两个内角的和)
∴ ∠2=∠C+∠E(三角形的一个外角等于和它不相邻的两个内角的和)
又∵∠A+∠1+∠2=180°(三角形内角和定理)
又∵ ∠2是△EHC的一个外角(外角的意义)
A
B
C
D
E
F
1
H
2
∴ ∠A+∠B+∠C+∠D+∠E =180°(等式性质)
例题欣赏
你认识外角吗
试一试
证明(1):∵ ∠BDC是△DCE的一个外角 (外角意义),
∴ ∠BDC>∠CED(三角形的一个外角大于和它不相邻的任何一个外角).
∴ ∠DEC>∠A(三角形的一个外角大于和它不相邻的任何一个外角).
∴ ∠BDC>∠A (不等式的性质).
∵ ∠DEC是△ABE的一个外角 (外角意义),
已知: 如图所示.
求证: (1)∠BDC>∠A;
(2) ∠BDC=∠A+∠B+∠C.
B
C
A
D
E
你认识外角吗
已知: 如图所示.
求证: (1)∠BDC>∠A;
(2) ∠BDC=∠A+∠B+∠C.
试一试
证明(2):∵ ∠BDC是△DCE的一个外角 (外角意义),
∴ ∠BDC =∠C+∠CED(三角形的一个外角等于和它不相邻的两个内角的和).
∴ ∠DEC=∠A+ ∠B(三角形的一个外角等于和它不相邻的两个外角的和).
∴ ∠BDC=∠A+∠B+∠C (等式的性质).
∵ ∠DEC是△ABE的一个外角 (外角意义),
B
C
A
D
E
回味无穷
理解几何命题证明的方法,步骤,格式及注意事项.
三角形内角和定理
三角形三个内角的和等于1800.△ABC中,
∠A+∠B+∠C=1800.
推论1: 三角形的一个外角等于和它不相邻的两个内角的和.
推论2: 三角形的一个外角大于任何一个和它不相邻的内角.
关注三角形的外角.
推论3: 直角三角形的两锐角互余.
你准备如何提高证明命题的能力呢
小结 拓展
1.如图:将正方形的四个顶点用线段连接,什么样的线段最短?研究发现,并非对角线最短,而是如图所示的连法最短(即用线段AE,DE,EF,BF,CF把四个顶点连接起来) .
已知图中∠DAE=∠ADE=300,∠AEF=∠BFE=1200 .
你能证明此时的AB∥EF吗?.
证明:∵∠DAB=900(正方形性质) ,∠DAE=300(已知),
∴∠BAE=600(等式性质).
∵∠AEF=1200(已知),
∴∠BAE+∠AEF=1800(等式性质) .
∴ AB∥EF(同旁内角相等,两直线平行).
A
B
C
D
1题图
E
F
“行家”看“门道”
∴∠2+∠4=1800 ( 两直线平行,同旁内角互补)
2.已知:如图,直线 a,b被 直线c所截,a∥b.
求证:∠1+∠2=1800.
b
a
c
2
1
2题图
证明1:∵ a∥b(已知)
∴∠2=∠3 (两直线平行,内错角相等)
3
又∵∠1+∠3= 1800 (平角意义)
∴∠1+∠2= 1800 (等量代换)
证明2:∵ a∥b(已知)
∠1=∠4 ( 对顶角相等)
∴∠1+∠2= 1800 (等量代换).
4
“行家”看“门道”
3.已知:如图,∠1+∠2=1800.
求证: ∠3=∠4.
分析:要证明∠3=∠4,只要证明CD∥EF ;而由∠1+∠2=1800,可得∠1+∠5=1800.从而可得CD∥EF
4
1
2
3
O
C
E
A
B
F
D
3题图
证明:∵ ∠1+∠2=1800 (已知) ,
5
∠5=∠2(对顶角相等),
∴∠1+∠5=1800 (等量代换).
∴ CD∥EF (同旁内角互补,两直线平行).
∴∠3=∠4(两直线平行,同位角相等).
“行家”看“门道”
知识的升华
作业:复习题
