2021年中考数学二轮复习几何模型加强版 专题01 中点相关的辅助线问题(Word版 含解析)
文档属性
| 名称 | 2021年中考数学二轮复习几何模型加强版 专题01 中点相关的辅助线问题(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 805.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 09:37:15 | ||
图片预览



文档简介
专题01 中点相关的辅助线问题
1.如图,在false中,false,false是中线,false是角平分线,点false是false上任意一点(不与false,false重合),连接false、false.给出以下结论:①false;②false;③false;④false.其中一定正确的有( )
A.false个 B.false个 C.false个 D.false个
【分析】①根据面积法可得false,false,从而可得①正确;②由false是中线,无法得出false,故可判断②错误;③运用SAS证明false得false,在false中运用三角形三边关系可得结论,从而判断③;④在false上截取false,连接false,运用false证明false得false,在false中运用三角形三边关系可得结论,从而判断④.
【解析】①过false作false于false,false于false,过false作false于false,
false是false角平分线,false,false,
false,false,false,false,false
false,false,故①正确;
②falsefalse,
false平分false,false,
false是中线,false无法得出false,故②错误;
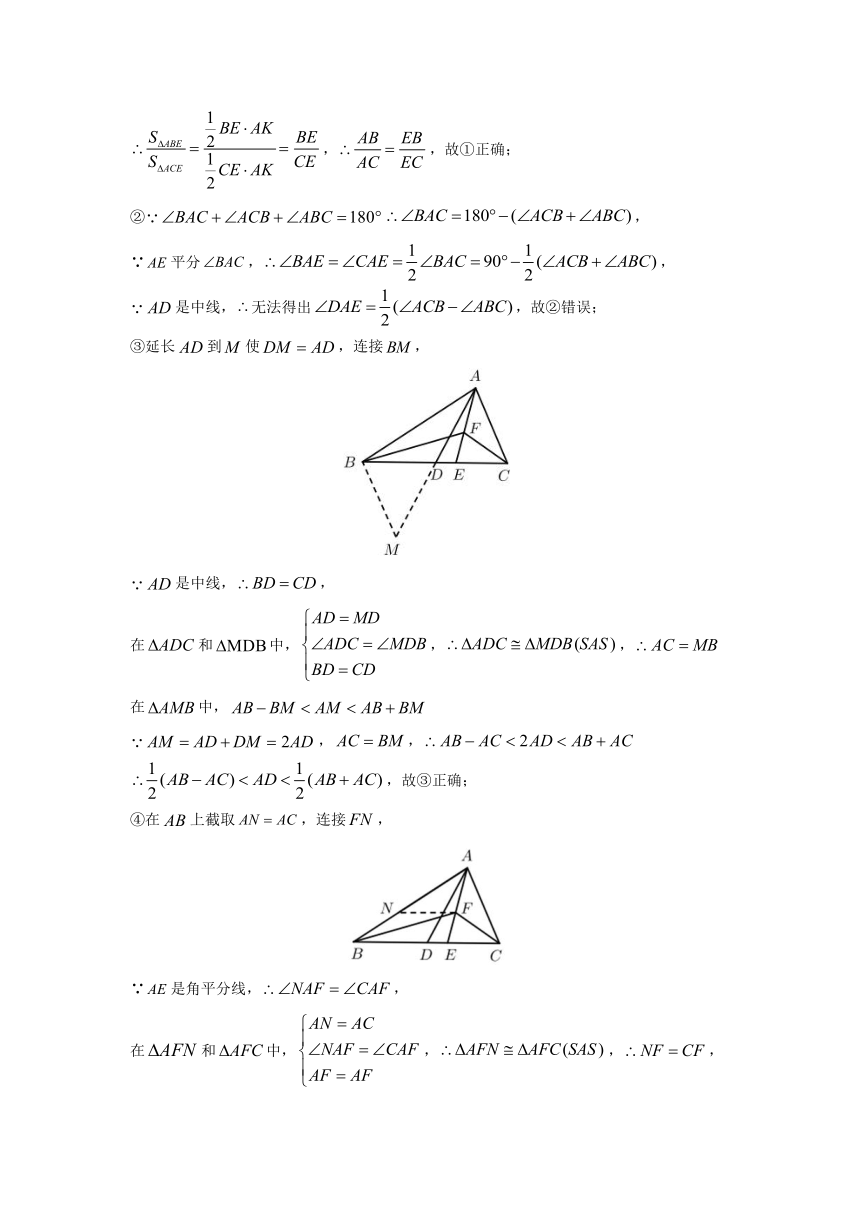
③延长false到false使false,连接false,
false是中线,false,
在false和false中,false,false,false
在false中,false
false,false,false
false,故③正确;
④在false上截取false,连接false,
false是角平分线,false,
在false和false中,false,false,false,
在false中,false,
false,false,
即false,故④正确;
综上①③④正确.故选B.
【小结】此题主要考查了三角形的中线,角平分线以及全等三角形的判定与性质,关键是正确画出辅助线.
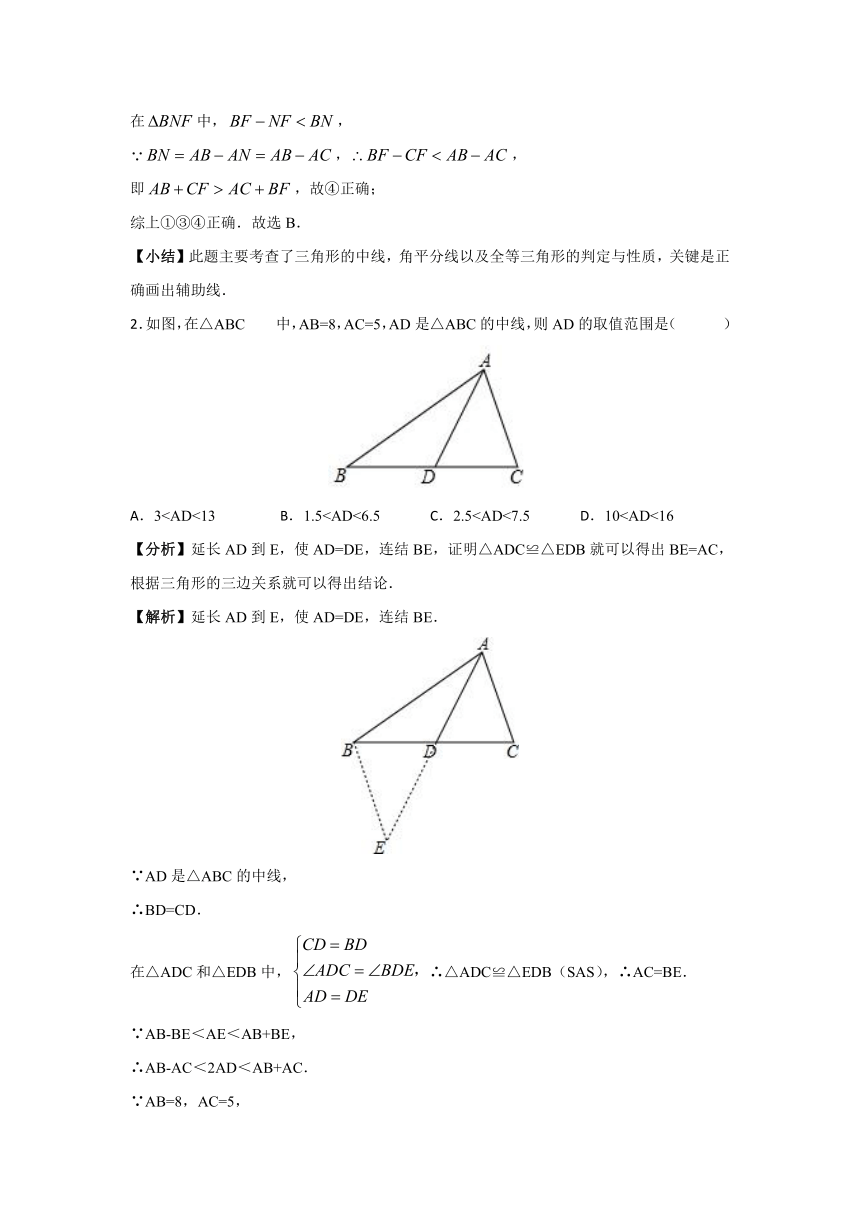
2.如图,在△ABC 中,AB=8,AC=5,AD是△ABC的中线,则AD的取值范围是( )
A.3【分析】延长AD到E,使AD=DE,连结BE,证明△ADC≌△EDB就可以得出BE=AC,根据三角形的三边关系就可以得出结论.
【解析】延长AD到E,使AD=DE,连结BE.
∵AD是△ABC的中线,
∴BD=CD.
在△ADC和△EDB中,false ∴△ADC≌△EDB(SAS),∴AC=BE.
∵AB-BE<AE<AB+BE,
∴AB-AC<2AD<AB+AC.
∵AB=8,AC=5,
∴1.5<AD<6.5.
故选:B
【小结】本题考查了全等三角形的判定及性质的运用,三角形的中线的性质的运用,三角形三边关系的性质的运用,解答时证明三角形全等是关键.
3.在△ABC中,AC=6,中线AD=5,则边AB的取值范围是( )
A.1<AB<11 B.4<AB<13 C.4<AB<16 D.11<AB<16
【分析】作出图形,延长AD至E,使DE=AD,然后利用“边角边”证明△ABD和△ECD全等,根据全等三角形对应边相等可得AB=CE,再利用三角形的任意两边之和大于第三边,三角形的任意两边之差小于第三边求出CE的取值范围,即为AB的取值范围.
【解析】如图,延长AD至E,使DE=AD,
∵AD是△ABC的中线,
∴BD=CD,
在△ABD和△ECD中,
BD=CD,∠ADB=∠EDC,AD=DE,
∴△ABD≌△ECD(SAS),
∴AB=CE,
∵AD=5,
∴AE=5+5=10,
∵10+6=16,10?6=4,
∴4<CE<16,
即4<AB<16.
故选:C.
【小结】本题考查了全等三角形的判定与性质,三角形的任意两边之和大于第三边,三角形的任意两边之差小于第三边,“遇中线,加倍延”构造出全等三角形是解题的关键.
4.在false中,false,false于点false,点false为false的中点,若false,则false的度数是( )
A.false B.false C.false D.false
【分析】连结CE,并延长CE,交BA的延长线于点N,根据已知条件和平行四边形的性质可证明△NAE≌△CFE,所以NE=CE,NA=CF,再由已知条件CD⊥AB于D,∠ADE=50°,即可求出∠B度数.
【解析】连结CE,并延长CE,交BA的延长线于点N,
∵四边形ABCF是平行四边形,
∴AB∥CF,AB=CF,∴∠NAE=∠F,
∵点E是的AF中点,∴AE=FE,
在△NAE和△CFE中,false ,∴△NAE≌△CFE(ASA),∴NE=CE,NA=CF,
∵AB=CF,∴NA=AB,即BN=2AB,
∵BC=2AB,∴BC=BN,∠N=∠NCB,
∵CD⊥AB于D,即∠NDC=90°且NE=CE,∴DE=falseNC=NE,
∴∠N=∠NDE=50°=∠NCB,∴∠B=80°.故选:D.
【小结】本题考查了平行四边形的性质,综合性较强,难度较大,解答本题的关键是正确作出辅助线,构造全等三角形,在利用等腰三角形的性质解答.
5.已知三角形的两边长分别为4和6,则第三边的中线长x的取值范围是_____.
【分析】由“SAS”可证△BDE≌△CDA,可得BE=AC=6,AE=2x,根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边,即可求解.
【解析】如图所示,AB=4,AC=6,延长AD至E,使AD=DE,连接BE、EC,设AD=x,
在△BDE与△CDA中,false,∴△BDE≌△CDA(SAS),∴BE=AC=6,AE=2x,
在△ABE中,BE﹣AB<AE<AB+BE,即6﹣4<2x<6+4,∴1<x<5,
【小结】考查全等三角形的判定与性质,解题的关键是根据题意构造全等三角形及三角形的三边关系.
6.如图,在矩形false中,false分别为边false,false的中点,false与false、false分别交于点false、false.已知false,false,则false的长为______________.
【分析】延长false,false交于false,已知false,false,则false,因为false为false中点,即可得false,通过false,根据对应边成比例可得FN、CN的长;同理延长false,false交于点false,即可求出CM的长,即可得MN.
【解析】延长false,false交于false,
∵四边形false为矩形,false,
∴false,false,false,
∵false为false中点,∴false,
在false中,false,由勾股定理得:false,
∵false,false,false为false中点,false,∴false,
在false与false中,false,∴,
∴,即,
∵,∴,∴,
∵,∴,,
延长,交于点,
∵为中点,∴,
在与中,,∴,∴,
∴,,
∴,∵,∴,
∴,∴,
∴,即的长度为.
【小结】本题考查全等三角形、相似三角形的判定与性质相结合,注意构造辅助线构造8字型全等及相似是解题的关键,属于中等偏难题型.
7.在中,是边上的中线,若,则长的取值范围是_________.
【分析】利用中线的性质,作辅助线AD=DE,构造全等三角形,再有全等三角形对应边相等的性质,解得,最后由三角形三边关系解题即可.
【解析】如图,AD为BC边上的中线,延长AD至点E,使得AD=DE
在△ADB和△EDC中,,,
故答案为:.
【小结】本题考查三角形三边的关系,其中涉及全等三角形的判定与性质等知识,是重要考点,掌握相关知识、正确作出辅助线是解题的关键.
8.在平行四边形中,为边的中点,且交射线于点,若,则的长度为________
【分析】延长AE交BC的延长线于点G,分两种情况:点F在线段BC上和点F在线段BC的延长线上,分情况讨论即可.
【解析】延长AE交BC的延长线于点G,分两种情况:
①如图
∵四边形ABCD是平行四边形,
∴.
,
,
.
点E为CD边的中点,,
在和中, ,, ,
,
;
②如图,
同理可得,,
,
,
;
综上所述,BF的长度为7或19,
故答案为:7或19.
【小结】本题主要考查平行四边形的性质和全等三角形的判定及性质,掌握这些性质并分情况讨论是解题的关键.
9.已知:在中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于CE于点F,交CD于点G(如图1),求证:AE=CG;
(2)直线AH垂直于CE,垂足为H,交CD的延长线于点M(如图2),求证:.
【分析】(1)运用等腰直角三角形性质,三线合一,可以得到△AEC和△CGB一组对应边、一组对应角相等,,;然后利用同角的余角相等,证得;两角及其夹边对应相等则两三角形全等.
(2)运用等腰直角三角形性质,三线合一,可以得到△BCE和△CAM一组对应边、一组对应角相等,,;然后利用同角的余角相等,证得;两角及其中一角的对边对应相等则两三角形全等.
【解析】(1)证明:∵点D是AB中点,AC=BC,∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,
∴∠CAD=∠CBD=45°,∴∠CAE=∠BCG,
又∵BF⊥CE,∴∠CBG+∠BCF=90°,
又∵∠ACE+∠BCF=90°,∴∠ACE=∠CBG,
在△AEC和△CGB中,,∴△AEC≌△CGB(ASA),∴AE=CG,
(2)证明:∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,∴∠CMA=∠BEC,
又∵∠ACM=∠CBE=45°,
在△BCE和△CAM中,,∴△BCE≌△CAM(AAS).
【小结】考查全等三角形判定定理,从题中找到对应边、角的信息,灵活运用三角形判定定理是解题关键.
10.已知,△ABC中,AC=BC,∠ACB=90°,CD为边AB上的中线,若E是线段CA上任意一点,DF⊥DE,交直线BC于F点.G为EF的中点,连接CG并延长交直线AB于点H.
(1)试说明:①AE=CF; ②CG=GD;
(2)若AE=6,CH=10,求边AC的长.
【分析】(1)①由题意易得AD=DC=DB,∠A=∠B=45°,CD⊥AB,进而可证△ADE≌△CDF,然后根据全等三角形的性质可得;②由直角三角形斜边中线定理可得,进而问题得证;
(2)由(1)可得AE=CF=6,由题意易得,则有EF=CH=10,然后根据勾股定理可求解.
【解析】(1)①AE=CF,理由如下:
∵AC=BC,∠ACB=90°,CD为边AB上的中线,
∴AD=DC=DB,∠A=∠B=45°,CD⊥AB,∴∠A=∠BCD=45°,
∵DF⊥DE,∴∠EDC+∠CDF=90°,
又∵∠ADE+∠EDC=90°,∴∠ADE=∠CDF,∴△ADE≌△CDF(ASA),∴AE=CF,
②CG=GD,理由如下:
∵∠ACB=90°,∠EDF=90°,EG=GF,∴,∴CG=GD;
(2)由(1)得:AE=CF=6,CG=GD,,∴∠GCD=∠GDC,
∵∠GCD+∠CHD=90°,∠GDC+∠GDH=90°,
∴∠CHD=∠GDH,∴GH=GD,∴,
∵CH=10,∴CH=EF=10,
在Rt△CEF中,,即,解得:CE=8,
∴AC=AE+CE=14.
【小结】本题主要考查等腰三角形的性质与判定、勾股定理及直角三角形斜边中线定理,熟练掌握等腰三角形的性质与判定、勾股定理及直角三角形斜边中线定理是解题的关键.
11.请阅读下列材料:
问题:在四边形ABCD中,M是BC边的中点,且∠AMD=90°
(1)如图1,若AB与CD不平行,试判断AB+CD与AD之间的数量关系;
小雪同学的思路是:延长DM至E使DM=ME,连接AE,BE,构造全等三角形,经过推理使问题得到解决请你参考小雪的思路,在图1中把图形补充完整,并直接写出上面问题AB+CD与AD之间的数量关系:
(2)如图2,若在原条件的基础上,增加AM平分∠BAD,(1)中结论还成立吗?若不成立,写出AB+CD与AD之间的数量关系,并证明.
【分析】(1)根据条件作出图形,利用DM=EM、BM=MC便可得到是四边形BECE是平行四边形,再结合EM=DM,且∠AMD=90°,得到等腰三角形,最后根据三角形三边关系求解.
(2)增加AM平分∠BAD,便可以得到点A.B.E必然共线,故(1)的结论不成立,通过(1)的分析,边可以证明其数量关系.
【解析】(1)AB与CD不平行
根据题意,延长DM使DM=EM,连接BE,AE,EC,BD
由于M是BC的中点,故BM=MC
∴四边形BECE是平行四边形
∴CD=BE
又 EM=DM,且∠AMD=90°
∴是等腰三角形
∴AD=AB
在中,
(2)若在原条件的基础上,增加AM平分∠BAD
则(1)的结论不成立
关系为:
证明:由于M是BC的中点,故BM=MC
∴四边形BECE是平行四边形
∴CD=BE
又 EM=DM,且∠AMD=90°
∴是等腰三角形
∴AD=AE
又AM平分∠BAD
∴点A.B.E必然共线
∴
【小结】本题比较综合,涉及到画图能力,平行四边形判定,等腰三角形性质应用,三角形三边关系等,解题的关键在于熟悉各个知识点的灵活运用.
12.如图,在△ABC中,AD是BC边上的中线.
(1)如果,,求证:△ABC是直角三角形.
(2)如果,,,,求BC的长.
【分析】(1)由于, 所以,故有,,由三角形内角和定理即可求解;
(2)延长AD到E使,可得,由勾股定理可得,再由勾股定理可求得CD的长,同时即可求解.
【解析】(1)∵,,
∴,
∴,,
∵,
∴,
即.
(2)延长AD到E使,连接CE,
在△ABD和△ECD中,,∴,
∴,,,
在△AEC中,,,,
∴,
∴,
由勾股定理得:,
∴.
【小结】主要考查三角形全等,利用倍长中线作出辅助线,由勾股定理证明是本题的解题关键.
13.如图,已知,点是的中点,且,求证:.
【分析】延长AE、BC交于点M,利用AAS证出△ADE≌△MCE,从而得出AD=MC,AE=ME,结合已知条件即可证出BM=AB,再利用SSS即可证出△BAE≌△BME,从而得出∠BEA=∠BEM,根据垂直定义即可证出结论.
【解析】延长AE、BC交于点M,如下图所示
∵点是的中点,∴DE=CE,
∵∴∠1=∠M
在△ADE和△MCE中,,∴△ADE≌△MCE,∴AD=MC,AE=ME
∵
∴MC+BC=AB,∴BM=AB
在△BAE和△BME中,,∴△BAE≌△BME,∴∠BEA=∠BEM
∵∠BEA+∠BEM=180°
∴∠BEA=∠BEM=90°
∴
【小结】此题考的是全等三角形的判定及性质、平行线的性质和垂直的定义,掌握全等三角形的判定及性质、平行线的性质和垂直的定义是解题关键.
14.如图,已知AD是的中线,过点B作BE⊥AD,垂足为E.若BE=6,求点C到AD的距离.
【分析】延长AD,过点C作于点F,证明,据全等性质得
【解析】如图,延长AD,过点C作于点F,
∵AD是的中线,∴,
∵,,∴,
在和中,,∴,
∴,即点C到AD的距离是6.
【小结】本题考查全等三角形的性质和判定,解题的关键是利用倍长中线的方法做辅助线构造全等三角形,利用全等三角形的性质求解.
15.△ ABC 中 D 是 BC 边上一点,连接 AD.
(1)如图1,AD 是中线,则 AB+AC 2AD(填 >,< 或 =);
(2)如图2,AD 是角平分线,求证 AB- AC > BD- CD.
【分析】(1)延长AD至E,使DE=AD,连接CE,利用“SAS”证明△CDE≌△ADB,再利用三角形的三边关系证明即可;
(2)在AB上截取AG=AC,连接DG,利用“SAS”证明△ADC△ADG,再根据三角形三边关系即可证明AB- AC > BD- CD.
【解析】(1)如图,延长AD至E,使DE=AD,连接CE,
在△CDE与△ADB中,,∴△CDE≌△ADB(SAS),∴AB=CE,
∴AB+AC=AC+CE>AE=2AD,即AB+AC>2AD;
(2)在AB上截取AG=AC,连接DG,
∵AD 是角平分线,∴∠1=∠2,
在△ADC和△ADG中,,∴△ADC△ADG(SAS),∴DC=DG,
∴AB- AC = AB- AG=BG > BD- DG = BD- CD.
【小结】本题主要考查了全等三角形的判定和性质,三角形三边的关系,添加辅助线构建全等三角形是解题的关键.
16.在ABC中,∠C=90°,AC>BC,D是AB的中点,E为直线AC上一动点,连接DE,过点D作DF⊥DE,交直线BC于点F,连接EF.
(1)如图1,当点E是线段AC的中点时,AE=2,BF=1,求EF的长;
(2)当点E在线段CA的延长线上时,依题意补全图形2,用等式表示AE,EF,BF之间的数量关系,并证明.
【分析】(1)由三角形的中位线定理得DE∥BC,DE=BC,进而证明四边形CEDF是矩形得DE=CF,得出CF,再根据勾股定理得结果;
(2)过点B作BM∥AC,与ED的延长线交于点M,连接MF,证明△ADE≌△BDM得AE=BM,DE=DM,由垂直平分线的判定定理得EF=MF,进而根据勾股定理得结论.
【解析】(1)∵D是AB的中点,E是线段AC的中点,
∴DE∥BC,DE=BC,
∵∠ACB=90°,
∴∠DEC=90°,
∵DF⊥DE,
∴∠EDF=90°,
∴四边形CEDF是矩形,
∴DE=CF=BC,
∴CF=BF=1,
∵CE=AE=2,
∴EF=;
(2)AE2+BF2=EF2.
证明:过点B作BM∥AC,与ED的延长线交于点M,连接MF,
则∠AED=∠BMD,∠CBM=∠ACB=90°,
∵D点是AB的中点,
∴AD=BD,
在△ADE和△BDM中,,∴△ADE≌△BDM(AAS),∴AE=BM,DE=DM,
∵DF⊥DE,
∴EF=MF,
∵BM2+BF2=MF2,
∴AE2+BF2=EF2.
【小结】本题主要考查了直角三角形的性质,全等三角形的性质与判定,勾股定理,垂直平分线的判定,关键在于构造全等三角形.
17.如图1,已知正方形和等腰,,,是线段上一点,取中点,连接、.
(1)探究与的数量与位置关系,并说明理由;
(2)如图2,将图1中的等腰绕点顺时针旋转,则(1)中的结论是否仍然成立?请说明理由;
(3)在(2)的条件下,若,求的最小值.
【分析】(1)首先根据正方形和等腰直角三角形的性质得出、、三点共线,然后利用直角三角形斜边中线的性质即可证明,然后利用等腰三角形的性质和三角形外角的性质即可得出,从而证明;
(2)延长至,使,连接交于,连接、,首先通过SAS证明,从而利用全等三角形的性质及平行线的判定证明,进而可利用正方形和等腰直角三角形的性质证明,从而可证明结论仍然成立;
(3)连接,首先根据题意确定当、、,在同一直线上时,有最小值,此时在上,然后根据平行四边形的判定及性质得出有最小值就是的长,最后利用勾股定理求解即可.
【解析】(1)且.
理由如下:如图1,连接.
∵正方形和等腰,
∴,
∴、、三点共线.
∵,为的中点,,
∴.
∴,.
∴,即,
∴.
(2)仍然成立.
理由如下:如图2,延长至,使,连接交于,连接、.
∵,,,∴,
∴,,∴.
∵是正方形,∴,.
∵是等腰直角三角形,
∴,,∴,
∴,,∴,∴为等腰直角三角形.
又∵,∴且.
(3)如下图,连接,
当、、,在同一直线上时,有最小值,此时在上,
∵,,
∴四边形是平行四边形,∴,由(2)知,∴,
即有最小值,就是的长,由勾股定理得.
【小结】本题主要考查四边形综合,掌握平行四边形的判定及性质,等腰三角形的性质,正方形的性质,全等三角形的判定及性质是解题的关键.
18.如图,在△ABC中,AB=AC,D为线段BC的延长线上一点,且DB=DA,BE⊥AD于点E,取BE的中点F,连接AF.
(1)若AC=,AE=,求BE的长;
(2)在(1)的条件下,如果∠D=45°,求△ABD的面积.
(3)若∠BAC=∠DAF,求证:2AF=AD;
【分析】(1)在Rt△AEB中,利用勾股定理即可解决问题;
(2)由∠D=45°可证得BE=DE,再利用三角的面积公式计算即可;
(3)如图,延长AF至M点,使AF=MF,连接BM,首先证明△AEF≌△MFB,再证明△ABM≌△ACD即可.
【解析】(1)解:∵AB=AC,AC=,
∴AB=,
∵BE⊥AD,AE=,
∴在Rt△AEB中,;
(2)解:∵BE⊥AD,∠D=45°,
∴∠EBD=∠D =45°,
∴BE=DE=,
∴AD=AE+DE=,
∴;
(3)证明:如图,延长AF至M点,使AF=MF,连接BM,
∵点F为BE的中点,
∴EF=BF,
在△AEF和△MBF中, ,∴△AEF≌△MBF(SAS),∴∠FAE=∠FMB,
∴AE∥MB,
∴∠EAB+∠ABM=180°,
∴∠ABM=180°﹣∠BAD,
又∵AB=AC,DB=DA,
∴∠ABC=∠ACB=∠BAD,
∴∠ACD=180°﹣∠ACB,
∴∠ABM=∠ACD.
又∵∠BAC=∠DAF,
∴∠BAC﹣∠MAC=∠DAF﹣∠MAC,
∴∠1=∠2.
在△ABM和△ACD中,,∴△ABM≌△ACD(ASA),∴AM=AD,
又∵AM=AF+MF=2AF,
∴2AF=AD.
【小结】本题考查全等三角形的判定和性质、等腰三角形的性质、勾股定理等知识,解题的关键是中线延长一倍,作出正确的辅助线构造全等三角形,属于常考题型.
19.阅读下面材料:
数学课上,老师给出了如下问题:
如图,AD为△ABC中线,点E在AC上,BE交AD于点F,AE=EF.求证:AC=BF.
经过讨论,同学们得到以下两种思路:
思路一如图①,添加辅助线后依据SAS可证得△ADC≌△GDB,再利用AE=EF可以进一步证得∠G=∠FAE=∠AFE=∠BFG,从而证明结论.
思路二如图②,添加辅助线后并利用AE=EF可证得∠G=∠BFG=∠AFE=∠FAE,再依据AAS可以进一步证得△ADC≌△GDB,从而证明结论.
完成下面问题:
(1)①思路一的辅助线的作法是: ;
②思路二的辅助线的作法是: .
(2)请你给出一种不同于以上两种思路的证明方法(要求:只写出辅助线的作法,并画出相应的图形,不需要写出证明过程).
【分析】(1)①依据SAS可证得△ADC≌△GDB,再利用AE=EF可以进一步证得∠G=∠FAE=∠AFE=∠BFG,从而证明结论.
②作BG=BF交AD的延长线于点G.利用AE=EF可证得∠G=∠BFG=∠AFE=∠FAE,再依据AAS可以进一步证得△ADC≌△GDB,从而证明结论.
(2)作BG∥AC交AD的延长线于G,证明△ADC≌△GDB(AAS),得出AC=BG,证出∠G=∠BFG,得出BG=BF,即可得出结论.
【解析】(1)①延长AD至点G,使DG=AD,连接BG,如图①,理由如下:
∵AD为△ABC中线,
∴BD=CD,
在△ADC和△GDB中,,∴△ADC≌△GDB(SAS),∴AC=BG,
∵AE=EF,∴∠CAD=∠EFA,
∵∠BFG=∠G,∠G=∠CAD,
∴∠G=∠BFG,
∴BG=BF,
∴AC=BF.
故答案为:延长AD至点G,使DG=AD,连接BG;
②作BG=BF交AD的延长线于点G,如图②.
理由如下:∵BG=BF,∴∠G=∠BFG,
∵AE=EF,∴∠EAF=∠EFA,又∵∠EFA=∠BFG,∴∠G=∠EAF,
在△ADC和△GDB中,,∴△ADC≌△GDB(AAS),∴AC=BG,∴AC=BF;
故答案为:作BG=BF交AD的延长线于点G;
(2)作BG∥AC交AD的延长线于G,如图③所示:则∠G=∠CAD,∵AD为△ABC中线,∴BD=CD,
在△ADC和△GDB中,,∴△ADC≌△GDB(AAS),∴AC=BG,
∵AE=EF,∴∠CAD=∠EFA,
∵∠BFG=∠EFA,∠G=∠CAD,∴∠G=∠BFG,∴BG=BF,∴AC=BF.
【小结】本题主要考查全等三角形的判定和性质、等腰三角形的性质、其中一般证明两个三角形全等共有四个定理:AAS、ASA、SAS、SSS,需要同学们灵活运用,解题的关键是学会做辅助线解决问题.
20.已知:如图,在中,,为的中点,、分别在、上,且于.求证:.
【分析】通过倍长线段,将、、转化到中,再证为直角三角形.
【解析】延长至,使,连结、,
,,
,
,,
,
,,
,
又,,
,
.
【小结】本题考查了全等三角形判定与性质,勾股定理,正确添加辅助线,熟练掌握相关知识是解题的关键.
21.如图所示,在中,为中线,,求的度数.
【分析】延长AD至E,使,连结,则,根据全等三角形的性质得EC=AB,,由AB=2AD可得EC=AE,可得△AEC是等腰直角三角形,即可得∠DAC的度数.
【解析】延长AD至E,使,连结,
∵BD=CD,∠ADB=∠EDC
∴,
∴EC=AB,,
∵AB=2AD,
∴AB=AE=EC
∴△AEC是等腰直角三角形,
∴∠DAC=45°.
故答案为45°.
【小结】本题考查全等三角形的判定与性质, 等腰直角三角形的性质,解题的关键是作辅助线构建全等三角形和等腰直角三角形.
1.如图,在false中,false,false是中线,false是角平分线,点false是false上任意一点(不与false,false重合),连接false、false.给出以下结论:①false;②false;③false;④false.其中一定正确的有( )
A.false个 B.false个 C.false个 D.false个
【分析】①根据面积法可得false,false,从而可得①正确;②由false是中线,无法得出false,故可判断②错误;③运用SAS证明false得false,在false中运用三角形三边关系可得结论,从而判断③;④在false上截取false,连接false,运用false证明false得false,在false中运用三角形三边关系可得结论,从而判断④.
【解析】①过false作false于false,false于false,过false作false于false,
false是false角平分线,false,false,
false,false,false,false,false
false,false,故①正确;
②falsefalse,
false平分false,false,
false是中线,false无法得出false,故②错误;
③延长false到false使false,连接false,
false是中线,false,
在false和false中,false,false,false
在false中,false
false,false,false
false,故③正确;
④在false上截取false,连接false,
false是角平分线,false,
在false和false中,false,false,false,
在false中,false,
false,false,
即false,故④正确;
综上①③④正确.故选B.
【小结】此题主要考查了三角形的中线,角平分线以及全等三角形的判定与性质,关键是正确画出辅助线.
2.如图,在△ABC 中,AB=8,AC=5,AD是△ABC的中线,则AD的取值范围是( )
A.3
【解析】延长AD到E,使AD=DE,连结BE.
∵AD是△ABC的中线,
∴BD=CD.
在△ADC和△EDB中,false ∴△ADC≌△EDB(SAS),∴AC=BE.
∵AB-BE<AE<AB+BE,
∴AB-AC<2AD<AB+AC.
∵AB=8,AC=5,
∴1.5<AD<6.5.
故选:B
【小结】本题考查了全等三角形的判定及性质的运用,三角形的中线的性质的运用,三角形三边关系的性质的运用,解答时证明三角形全等是关键.
3.在△ABC中,AC=6,中线AD=5,则边AB的取值范围是( )
A.1<AB<11 B.4<AB<13 C.4<AB<16 D.11<AB<16
【分析】作出图形,延长AD至E,使DE=AD,然后利用“边角边”证明△ABD和△ECD全等,根据全等三角形对应边相等可得AB=CE,再利用三角形的任意两边之和大于第三边,三角形的任意两边之差小于第三边求出CE的取值范围,即为AB的取值范围.
【解析】如图,延长AD至E,使DE=AD,
∵AD是△ABC的中线,
∴BD=CD,
在△ABD和△ECD中,
BD=CD,∠ADB=∠EDC,AD=DE,
∴△ABD≌△ECD(SAS),
∴AB=CE,
∵AD=5,
∴AE=5+5=10,
∵10+6=16,10?6=4,
∴4<CE<16,
即4<AB<16.
故选:C.
【小结】本题考查了全等三角形的判定与性质,三角形的任意两边之和大于第三边,三角形的任意两边之差小于第三边,“遇中线,加倍延”构造出全等三角形是解题的关键.
4.在false中,false,false于点false,点false为false的中点,若false,则false的度数是( )
A.false B.false C.false D.false
【分析】连结CE,并延长CE,交BA的延长线于点N,根据已知条件和平行四边形的性质可证明△NAE≌△CFE,所以NE=CE,NA=CF,再由已知条件CD⊥AB于D,∠ADE=50°,即可求出∠B度数.
【解析】连结CE,并延长CE,交BA的延长线于点N,
∵四边形ABCF是平行四边形,
∴AB∥CF,AB=CF,∴∠NAE=∠F,
∵点E是的AF中点,∴AE=FE,
在△NAE和△CFE中,false ,∴△NAE≌△CFE(ASA),∴NE=CE,NA=CF,
∵AB=CF,∴NA=AB,即BN=2AB,
∵BC=2AB,∴BC=BN,∠N=∠NCB,
∵CD⊥AB于D,即∠NDC=90°且NE=CE,∴DE=falseNC=NE,
∴∠N=∠NDE=50°=∠NCB,∴∠B=80°.故选:D.
【小结】本题考查了平行四边形的性质,综合性较强,难度较大,解答本题的关键是正确作出辅助线,构造全等三角形,在利用等腰三角形的性质解答.
5.已知三角形的两边长分别为4和6,则第三边的中线长x的取值范围是_____.
【分析】由“SAS”可证△BDE≌△CDA,可得BE=AC=6,AE=2x,根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边,即可求解.
【解析】如图所示,AB=4,AC=6,延长AD至E,使AD=DE,连接BE、EC,设AD=x,
在△BDE与△CDA中,false,∴△BDE≌△CDA(SAS),∴BE=AC=6,AE=2x,
在△ABE中,BE﹣AB<AE<AB+BE,即6﹣4<2x<6+4,∴1<x<5,
【小结】考查全等三角形的判定与性质,解题的关键是根据题意构造全等三角形及三角形的三边关系.
6.如图,在矩形false中,false分别为边false,false的中点,false与false、false分别交于点false、false.已知false,false,则false的长为______________.
【分析】延长false,false交于false,已知false,false,则false,因为false为false中点,即可得false,通过false,根据对应边成比例可得FN、CN的长;同理延长false,false交于点false,即可求出CM的长,即可得MN.
【解析】延长false,false交于false,
∵四边形false为矩形,false,
∴false,false,false,
∵false为false中点,∴false,
在false中,false,由勾股定理得:false,
∵false,false,false为false中点,false,∴false,
在false与false中,false,∴,
∴,即,
∵,∴,∴,
∵,∴,,
延长,交于点,
∵为中点,∴,
在与中,,∴,∴,
∴,,
∴,∵,∴,
∴,∴,
∴,即的长度为.
【小结】本题考查全等三角形、相似三角形的判定与性质相结合,注意构造辅助线构造8字型全等及相似是解题的关键,属于中等偏难题型.
7.在中,是边上的中线,若,则长的取值范围是_________.
【分析】利用中线的性质,作辅助线AD=DE,构造全等三角形,再有全等三角形对应边相等的性质,解得,最后由三角形三边关系解题即可.
【解析】如图,AD为BC边上的中线,延长AD至点E,使得AD=DE
在△ADB和△EDC中,,,
故答案为:.
【小结】本题考查三角形三边的关系,其中涉及全等三角形的判定与性质等知识,是重要考点,掌握相关知识、正确作出辅助线是解题的关键.
8.在平行四边形中,为边的中点,且交射线于点,若,则的长度为________
【分析】延长AE交BC的延长线于点G,分两种情况:点F在线段BC上和点F在线段BC的延长线上,分情况讨论即可.
【解析】延长AE交BC的延长线于点G,分两种情况:
①如图
∵四边形ABCD是平行四边形,
∴.
,
,
.
点E为CD边的中点,,
在和中, ,, ,
,
;
②如图,
同理可得,,
,
,
;
综上所述,BF的长度为7或19,
故答案为:7或19.
【小结】本题主要考查平行四边形的性质和全等三角形的判定及性质,掌握这些性质并分情况讨论是解题的关键.
9.已知:在中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于CE于点F,交CD于点G(如图1),求证:AE=CG;
(2)直线AH垂直于CE,垂足为H,交CD的延长线于点M(如图2),求证:.
【分析】(1)运用等腰直角三角形性质,三线合一,可以得到△AEC和△CGB一组对应边、一组对应角相等,,;然后利用同角的余角相等,证得;两角及其夹边对应相等则两三角形全等.
(2)运用等腰直角三角形性质,三线合一,可以得到△BCE和△CAM一组对应边、一组对应角相等,,;然后利用同角的余角相等,证得;两角及其中一角的对边对应相等则两三角形全等.
【解析】(1)证明:∵点D是AB中点,AC=BC,∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,
∴∠CAD=∠CBD=45°,∴∠CAE=∠BCG,
又∵BF⊥CE,∴∠CBG+∠BCF=90°,
又∵∠ACE+∠BCF=90°,∴∠ACE=∠CBG,
在△AEC和△CGB中,,∴△AEC≌△CGB(ASA),∴AE=CG,
(2)证明:∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,∴∠CMA=∠BEC,
又∵∠ACM=∠CBE=45°,
在△BCE和△CAM中,,∴△BCE≌△CAM(AAS).
【小结】考查全等三角形判定定理,从题中找到对应边、角的信息,灵活运用三角形判定定理是解题关键.
10.已知,△ABC中,AC=BC,∠ACB=90°,CD为边AB上的中线,若E是线段CA上任意一点,DF⊥DE,交直线BC于F点.G为EF的中点,连接CG并延长交直线AB于点H.
(1)试说明:①AE=CF; ②CG=GD;
(2)若AE=6,CH=10,求边AC的长.
【分析】(1)①由题意易得AD=DC=DB,∠A=∠B=45°,CD⊥AB,进而可证△ADE≌△CDF,然后根据全等三角形的性质可得;②由直角三角形斜边中线定理可得,进而问题得证;
(2)由(1)可得AE=CF=6,由题意易得,则有EF=CH=10,然后根据勾股定理可求解.
【解析】(1)①AE=CF,理由如下:
∵AC=BC,∠ACB=90°,CD为边AB上的中线,
∴AD=DC=DB,∠A=∠B=45°,CD⊥AB,∴∠A=∠BCD=45°,
∵DF⊥DE,∴∠EDC+∠CDF=90°,
又∵∠ADE+∠EDC=90°,∴∠ADE=∠CDF,∴△ADE≌△CDF(ASA),∴AE=CF,
②CG=GD,理由如下:
∵∠ACB=90°,∠EDF=90°,EG=GF,∴,∴CG=GD;
(2)由(1)得:AE=CF=6,CG=GD,,∴∠GCD=∠GDC,
∵∠GCD+∠CHD=90°,∠GDC+∠GDH=90°,
∴∠CHD=∠GDH,∴GH=GD,∴,
∵CH=10,∴CH=EF=10,
在Rt△CEF中,,即,解得:CE=8,
∴AC=AE+CE=14.
【小结】本题主要考查等腰三角形的性质与判定、勾股定理及直角三角形斜边中线定理,熟练掌握等腰三角形的性质与判定、勾股定理及直角三角形斜边中线定理是解题的关键.
11.请阅读下列材料:
问题:在四边形ABCD中,M是BC边的中点,且∠AMD=90°
(1)如图1,若AB与CD不平行,试判断AB+CD与AD之间的数量关系;
小雪同学的思路是:延长DM至E使DM=ME,连接AE,BE,构造全等三角形,经过推理使问题得到解决请你参考小雪的思路,在图1中把图形补充完整,并直接写出上面问题AB+CD与AD之间的数量关系:
(2)如图2,若在原条件的基础上,增加AM平分∠BAD,(1)中结论还成立吗?若不成立,写出AB+CD与AD之间的数量关系,并证明.
【分析】(1)根据条件作出图形,利用DM=EM、BM=MC便可得到是四边形BECE是平行四边形,再结合EM=DM,且∠AMD=90°,得到等腰三角形,最后根据三角形三边关系求解.
(2)增加AM平分∠BAD,便可以得到点A.B.E必然共线,故(1)的结论不成立,通过(1)的分析,边可以证明其数量关系.
【解析】(1)AB与CD不平行
根据题意,延长DM使DM=EM,连接BE,AE,EC,BD
由于M是BC的中点,故BM=MC
∴四边形BECE是平行四边形
∴CD=BE
又 EM=DM,且∠AMD=90°
∴是等腰三角形
∴AD=AB
在中,
(2)若在原条件的基础上,增加AM平分∠BAD
则(1)的结论不成立
关系为:
证明:由于M是BC的中点,故BM=MC
∴四边形BECE是平行四边形
∴CD=BE
又 EM=DM,且∠AMD=90°
∴是等腰三角形
∴AD=AE
又AM平分∠BAD
∴点A.B.E必然共线
∴
【小结】本题比较综合,涉及到画图能力,平行四边形判定,等腰三角形性质应用,三角形三边关系等,解题的关键在于熟悉各个知识点的灵活运用.
12.如图,在△ABC中,AD是BC边上的中线.
(1)如果,,求证:△ABC是直角三角形.
(2)如果,,,,求BC的长.
【分析】(1)由于, 所以,故有,,由三角形内角和定理即可求解;
(2)延长AD到E使,可得,由勾股定理可得,再由勾股定理可求得CD的长,同时即可求解.
【解析】(1)∵,,
∴,
∴,,
∵,
∴,
即.
(2)延长AD到E使,连接CE,
在△ABD和△ECD中,,∴,
∴,,,
在△AEC中,,,,
∴,
∴,
由勾股定理得:,
∴.
【小结】主要考查三角形全等,利用倍长中线作出辅助线,由勾股定理证明是本题的解题关键.
13.如图,已知,点是的中点,且,求证:.
【分析】延长AE、BC交于点M,利用AAS证出△ADE≌△MCE,从而得出AD=MC,AE=ME,结合已知条件即可证出BM=AB,再利用SSS即可证出△BAE≌△BME,从而得出∠BEA=∠BEM,根据垂直定义即可证出结论.
【解析】延长AE、BC交于点M,如下图所示
∵点是的中点,∴DE=CE,
∵∴∠1=∠M
在△ADE和△MCE中,,∴△ADE≌△MCE,∴AD=MC,AE=ME
∵
∴MC+BC=AB,∴BM=AB
在△BAE和△BME中,,∴△BAE≌△BME,∴∠BEA=∠BEM
∵∠BEA+∠BEM=180°
∴∠BEA=∠BEM=90°
∴
【小结】此题考的是全等三角形的判定及性质、平行线的性质和垂直的定义,掌握全等三角形的判定及性质、平行线的性质和垂直的定义是解题关键.
14.如图,已知AD是的中线,过点B作BE⊥AD,垂足为E.若BE=6,求点C到AD的距离.
【分析】延长AD,过点C作于点F,证明,据全等性质得
【解析】如图,延长AD,过点C作于点F,
∵AD是的中线,∴,
∵,,∴,
在和中,,∴,
∴,即点C到AD的距离是6.
【小结】本题考查全等三角形的性质和判定,解题的关键是利用倍长中线的方法做辅助线构造全等三角形,利用全等三角形的性质求解.
15.△ ABC 中 D 是 BC 边上一点,连接 AD.
(1)如图1,AD 是中线,则 AB+AC 2AD(填 >,< 或 =);
(2)如图2,AD 是角平分线,求证 AB- AC > BD- CD.
【分析】(1)延长AD至E,使DE=AD,连接CE,利用“SAS”证明△CDE≌△ADB,再利用三角形的三边关系证明即可;
(2)在AB上截取AG=AC,连接DG,利用“SAS”证明△ADC△ADG,再根据三角形三边关系即可证明AB- AC > BD- CD.
【解析】(1)如图,延长AD至E,使DE=AD,连接CE,
在△CDE与△ADB中,,∴△CDE≌△ADB(SAS),∴AB=CE,
∴AB+AC=AC+CE>AE=2AD,即AB+AC>2AD;
(2)在AB上截取AG=AC,连接DG,
∵AD 是角平分线,∴∠1=∠2,
在△ADC和△ADG中,,∴△ADC△ADG(SAS),∴DC=DG,
∴AB- AC = AB- AG=BG > BD- DG = BD- CD.
【小结】本题主要考查了全等三角形的判定和性质,三角形三边的关系,添加辅助线构建全等三角形是解题的关键.
16.在ABC中,∠C=90°,AC>BC,D是AB的中点,E为直线AC上一动点,连接DE,过点D作DF⊥DE,交直线BC于点F,连接EF.
(1)如图1,当点E是线段AC的中点时,AE=2,BF=1,求EF的长;
(2)当点E在线段CA的延长线上时,依题意补全图形2,用等式表示AE,EF,BF之间的数量关系,并证明.
【分析】(1)由三角形的中位线定理得DE∥BC,DE=BC,进而证明四边形CEDF是矩形得DE=CF,得出CF,再根据勾股定理得结果;
(2)过点B作BM∥AC,与ED的延长线交于点M,连接MF,证明△ADE≌△BDM得AE=BM,DE=DM,由垂直平分线的判定定理得EF=MF,进而根据勾股定理得结论.
【解析】(1)∵D是AB的中点,E是线段AC的中点,
∴DE∥BC,DE=BC,
∵∠ACB=90°,
∴∠DEC=90°,
∵DF⊥DE,
∴∠EDF=90°,
∴四边形CEDF是矩形,
∴DE=CF=BC,
∴CF=BF=1,
∵CE=AE=2,
∴EF=;
(2)AE2+BF2=EF2.
证明:过点B作BM∥AC,与ED的延长线交于点M,连接MF,
则∠AED=∠BMD,∠CBM=∠ACB=90°,
∵D点是AB的中点,
∴AD=BD,
在△ADE和△BDM中,,∴△ADE≌△BDM(AAS),∴AE=BM,DE=DM,
∵DF⊥DE,
∴EF=MF,
∵BM2+BF2=MF2,
∴AE2+BF2=EF2.
【小结】本题主要考查了直角三角形的性质,全等三角形的性质与判定,勾股定理,垂直平分线的判定,关键在于构造全等三角形.
17.如图1,已知正方形和等腰,,,是线段上一点,取中点,连接、.
(1)探究与的数量与位置关系,并说明理由;
(2)如图2,将图1中的等腰绕点顺时针旋转,则(1)中的结论是否仍然成立?请说明理由;
(3)在(2)的条件下,若,求的最小值.
【分析】(1)首先根据正方形和等腰直角三角形的性质得出、、三点共线,然后利用直角三角形斜边中线的性质即可证明,然后利用等腰三角形的性质和三角形外角的性质即可得出,从而证明;
(2)延长至,使,连接交于,连接、,首先通过SAS证明,从而利用全等三角形的性质及平行线的判定证明,进而可利用正方形和等腰直角三角形的性质证明,从而可证明结论仍然成立;
(3)连接,首先根据题意确定当、、,在同一直线上时,有最小值,此时在上,然后根据平行四边形的判定及性质得出有最小值就是的长,最后利用勾股定理求解即可.
【解析】(1)且.
理由如下:如图1,连接.
∵正方形和等腰,
∴,
∴、、三点共线.
∵,为的中点,,
∴.
∴,.
∴,即,
∴.
(2)仍然成立.
理由如下:如图2,延长至,使,连接交于,连接、.
∵,,,∴,
∴,,∴.
∵是正方形,∴,.
∵是等腰直角三角形,
∴,,∴,
∴,,∴,∴为等腰直角三角形.
又∵,∴且.
(3)如下图,连接,
当、、,在同一直线上时,有最小值,此时在上,
∵,,
∴四边形是平行四边形,∴,由(2)知,∴,
即有最小值,就是的长,由勾股定理得.
【小结】本题主要考查四边形综合,掌握平行四边形的判定及性质,等腰三角形的性质,正方形的性质,全等三角形的判定及性质是解题的关键.
18.如图,在△ABC中,AB=AC,D为线段BC的延长线上一点,且DB=DA,BE⊥AD于点E,取BE的中点F,连接AF.
(1)若AC=,AE=,求BE的长;
(2)在(1)的条件下,如果∠D=45°,求△ABD的面积.
(3)若∠BAC=∠DAF,求证:2AF=AD;
【分析】(1)在Rt△AEB中,利用勾股定理即可解决问题;
(2)由∠D=45°可证得BE=DE,再利用三角的面积公式计算即可;
(3)如图,延长AF至M点,使AF=MF,连接BM,首先证明△AEF≌△MFB,再证明△ABM≌△ACD即可.
【解析】(1)解:∵AB=AC,AC=,
∴AB=,
∵BE⊥AD,AE=,
∴在Rt△AEB中,;
(2)解:∵BE⊥AD,∠D=45°,
∴∠EBD=∠D =45°,
∴BE=DE=,
∴AD=AE+DE=,
∴;
(3)证明:如图,延长AF至M点,使AF=MF,连接BM,
∵点F为BE的中点,
∴EF=BF,
在△AEF和△MBF中, ,∴△AEF≌△MBF(SAS),∴∠FAE=∠FMB,
∴AE∥MB,
∴∠EAB+∠ABM=180°,
∴∠ABM=180°﹣∠BAD,
又∵AB=AC,DB=DA,
∴∠ABC=∠ACB=∠BAD,
∴∠ACD=180°﹣∠ACB,
∴∠ABM=∠ACD.
又∵∠BAC=∠DAF,
∴∠BAC﹣∠MAC=∠DAF﹣∠MAC,
∴∠1=∠2.
在△ABM和△ACD中,,∴△ABM≌△ACD(ASA),∴AM=AD,
又∵AM=AF+MF=2AF,
∴2AF=AD.
【小结】本题考查全等三角形的判定和性质、等腰三角形的性质、勾股定理等知识,解题的关键是中线延长一倍,作出正确的辅助线构造全等三角形,属于常考题型.
19.阅读下面材料:
数学课上,老师给出了如下问题:
如图,AD为△ABC中线,点E在AC上,BE交AD于点F,AE=EF.求证:AC=BF.
经过讨论,同学们得到以下两种思路:
思路一如图①,添加辅助线后依据SAS可证得△ADC≌△GDB,再利用AE=EF可以进一步证得∠G=∠FAE=∠AFE=∠BFG,从而证明结论.
思路二如图②,添加辅助线后并利用AE=EF可证得∠G=∠BFG=∠AFE=∠FAE,再依据AAS可以进一步证得△ADC≌△GDB,从而证明结论.
完成下面问题:
(1)①思路一的辅助线的作法是: ;
②思路二的辅助线的作法是: .
(2)请你给出一种不同于以上两种思路的证明方法(要求:只写出辅助线的作法,并画出相应的图形,不需要写出证明过程).
【分析】(1)①依据SAS可证得△ADC≌△GDB,再利用AE=EF可以进一步证得∠G=∠FAE=∠AFE=∠BFG,从而证明结论.
②作BG=BF交AD的延长线于点G.利用AE=EF可证得∠G=∠BFG=∠AFE=∠FAE,再依据AAS可以进一步证得△ADC≌△GDB,从而证明结论.
(2)作BG∥AC交AD的延长线于G,证明△ADC≌△GDB(AAS),得出AC=BG,证出∠G=∠BFG,得出BG=BF,即可得出结论.
【解析】(1)①延长AD至点G,使DG=AD,连接BG,如图①,理由如下:
∵AD为△ABC中线,
∴BD=CD,
在△ADC和△GDB中,,∴△ADC≌△GDB(SAS),∴AC=BG,
∵AE=EF,∴∠CAD=∠EFA,
∵∠BFG=∠G,∠G=∠CAD,
∴∠G=∠BFG,
∴BG=BF,
∴AC=BF.
故答案为:延长AD至点G,使DG=AD,连接BG;
②作BG=BF交AD的延长线于点G,如图②.
理由如下:∵BG=BF,∴∠G=∠BFG,
∵AE=EF,∴∠EAF=∠EFA,又∵∠EFA=∠BFG,∴∠G=∠EAF,
在△ADC和△GDB中,,∴△ADC≌△GDB(AAS),∴AC=BG,∴AC=BF;
故答案为:作BG=BF交AD的延长线于点G;
(2)作BG∥AC交AD的延长线于G,如图③所示:则∠G=∠CAD,∵AD为△ABC中线,∴BD=CD,
在△ADC和△GDB中,,∴△ADC≌△GDB(AAS),∴AC=BG,
∵AE=EF,∴∠CAD=∠EFA,
∵∠BFG=∠EFA,∠G=∠CAD,∴∠G=∠BFG,∴BG=BF,∴AC=BF.
【小结】本题主要考查全等三角形的判定和性质、等腰三角形的性质、其中一般证明两个三角形全等共有四个定理:AAS、ASA、SAS、SSS,需要同学们灵活运用,解题的关键是学会做辅助线解决问题.
20.已知:如图,在中,,为的中点,、分别在、上,且于.求证:.
【分析】通过倍长线段,将、、转化到中,再证为直角三角形.
【解析】延长至,使,连结、,
,,
,
,,
,
,,
,
又,,
,
.
【小结】本题考查了全等三角形判定与性质,勾股定理,正确添加辅助线,熟练掌握相关知识是解题的关键.
21.如图所示,在中,为中线,,求的度数.
【分析】延长AD至E,使,连结,则,根据全等三角形的性质得EC=AB,,由AB=2AD可得EC=AE,可得△AEC是等腰直角三角形,即可得∠DAC的度数.
【解析】延长AD至E,使,连结,
∵BD=CD,∠ADB=∠EDC
∴,
∴EC=AB,,
∵AB=2AD,
∴AB=AE=EC
∴△AEC是等腰直角三角形,
∴∠DAC=45°.
故答案为45°.
【小结】本题考查全等三角形的判定与性质, 等腰直角三角形的性质,解题的关键是作辅助线构建全等三角形和等腰直角三角形.
同课章节目录
