安徽省六安市示范高中2021届高三上学期期末教学质量检测数学(文)试题 Word版含答案
文档属性
| 名称 | 安徽省六安市示范高中2021届高三上学期期末教学质量检测数学(文)试题 Word版含答案 |

|
|
| 格式 | doc | ||
| 文件大小 | 851.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 00:00:00 | ||
图片预览



文档简介
2021年六安市省示范高中高三教学质量检测
文科数学试题
注意事项:
1.答题前,考生务必将自己的姓名、座位号等填写在答题卡和答题卷指定位置上.
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦于净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上,写在本试卷上无效
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知复数(i为虚数单位),则在复平面内对应的点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 已知集合,,则( )
A. B. C. D.
3. 设,,则( )
A. B. C. D.
4. 已知命题,,则p是q的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
5. 已知函数的部分图象如图所示,则的解析式可能为( )
A. B.
C. D.
6. 已知,,C在抛物线上,且到焦点距离为5,则的面积为( )
A. 4 B. 5 C. 8 D. 10
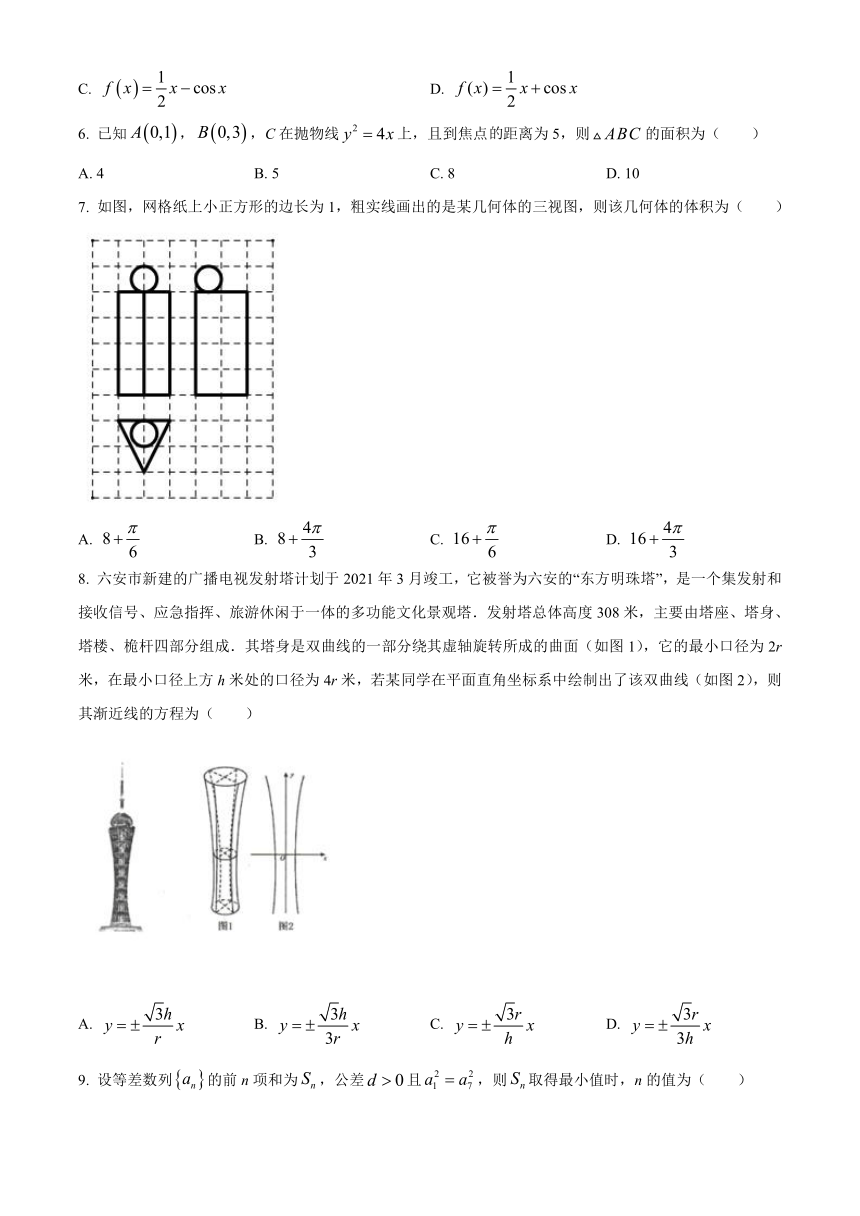
7. 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为( )
A. B. C. D.
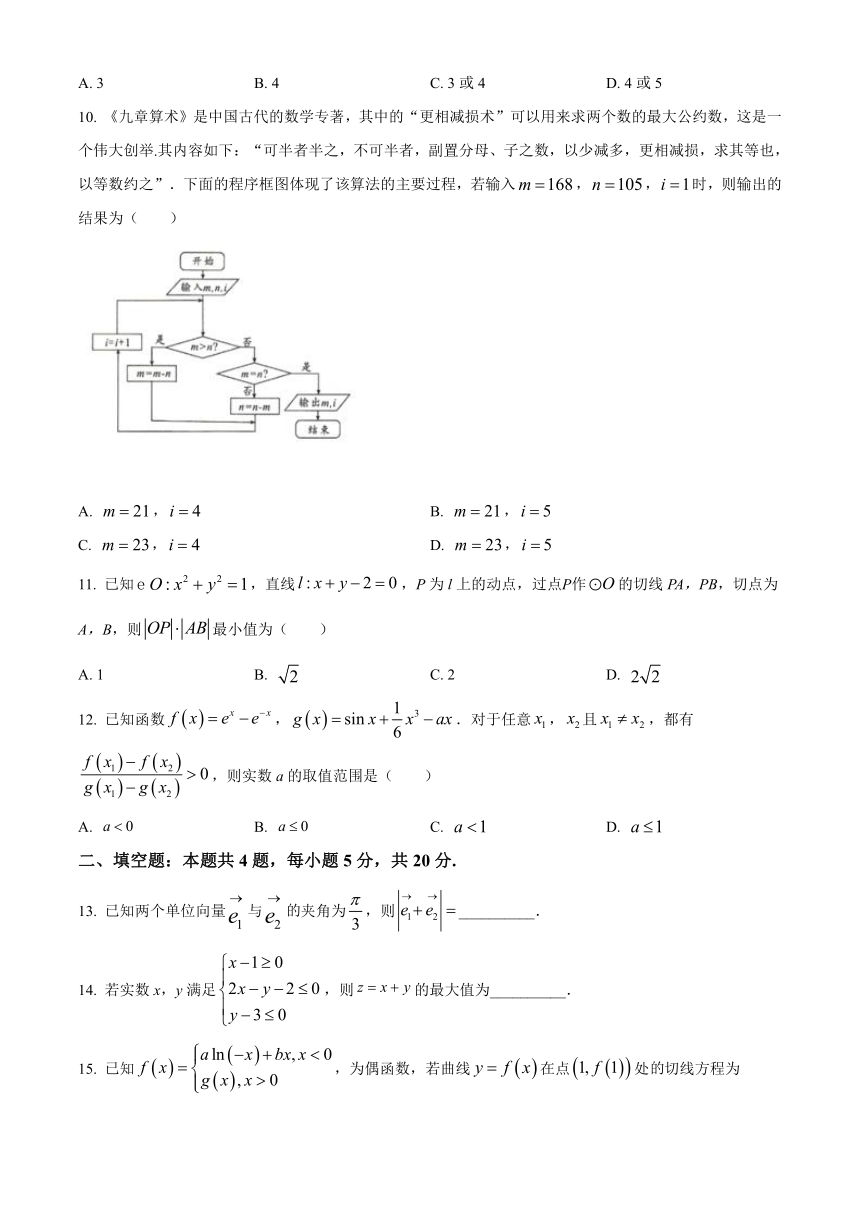
8. 六安市新建的广播电视发射塔计划于2021年3月竣工,它被誉为六安的“东方明珠塔”,是一个集发射和接收信号、应急指挥、旅游休闲于一体的多功能文化景观塔.发射塔总体高度308米,主要由塔座、塔身、塔楼、桅杆四部分组成.其塔身是双曲线的一部分绕其虚轴旋转所成的曲面(如图1),它的最小口径为2r米,在最小口径上方h米处的口径为4r米,若某同学在平面直角坐标系中绘制出了该双曲线(如图2),则其渐近线的方程为( )
A. B. C. D.
9. 设等差数列的前n项和为,公差且,则取得最小值时,n的值为( )
A. 3 B. 4 C. 3或4 D. 4或5
10. 《九章算术》是中国古代的数学专著,其中的“更相减损术”可以用来求两个数的最大公约数,这是一个伟大创举.其内容如下:“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也,以等数约之”.下面的程序框图体现了该算法的主要过程,若输入,,时,则输出的结果为( )
A. , B. ,
C. , D. ,
11. 已知,直线,P为l上的动点,过点Р作的切线PA,PB,切点为A,B,则最小值为( )
A. 1 B. C. 2 D.
12. 已知函数,.对于任意,且,都有,则实数a的取值范围是( )
A. B. C. D.
二、填空题:本题共4题,每小题5分,共20分.
13. 已知两个单位向量与夹角为,则__________.
14. 若实数x,y满足,则的最大值为__________.
15. 已知,为偶函数,若曲线在点处切线方程为,则__________.
16. 图,在中,,垂足为D,,垂足为E.现将沿AD折起,使得,若三棱锥外接球的球心为О,半径为1,则面积的最大值为___________.
三、解答题:本题共6小题,共70分.解答须写出文字说明、证明过程和演算步骤.
17. 从下列①②③选项中,选择其中一个作为条件进行解答:
①已知数列的前n项和;
②已知数列是等比数列,,;
③已知数列中,,且对任意的正整数m,n都有.
(1)求数列的通项公式;
(2)已知,求数列的前2021项的和.
18. 已知函数.
(1)求函数的单调递增区间;
(2)将函数图象上所有点的横坐标缩短到原来的倍(纵坐标不变),再把图象向右平移个单位长度,得到函数的图象,当时,求函数的值域.
.
19. 如图,在四棱锥中,平面ABCD.,,,E是PD的中点.
(1)证明:平面PBC;
(2)若,求三棱锥的体积.
20. 为积极响应国家对垃圾分类处理的号召,增强市民的环保意识,加快城市生态文明的建设,某市决定在A,B,C三个社区进行垃圾分类回收试点,现准备建造一座垃圾处理站D,集中处理三个社区的湿垃圾.如图,已知千米,千米,,.
(1)求垃圾处理站D与社区A之间距离;
(2)假设有大、小两种运输车,负责在各社区和垃圾处理站之间运输湿垃圾,车在运输期间都是直线行驶,每辆大车的行车费用为每千米a元,每辆小车的行车费用为每千米元().
现有两种运输湿垃圾的方案
方案一:用一辆大车运输,从D出发,依次经A,B,C,再由C返回到D;
方案二:用三辆小车运输,均从D出发.分别到A,B,C,再各自原路返回到D.
请从行车费用的角度比较哪种方案更合算,并说明理由.
21. 已知函数,
(1)若,的极大值是,求a的值;
(2)若,在上存在唯一零点,求b的值.
22. 已知椭圆的离心率为,短轴长为.
(1)求椭圆C的方程;
(2)设A,B分别为椭圆C的左、右顶点,若过点且斜率不为0的直线l与椭圆C交于M、N两点,直线AM与BN相交于点Q.证明:点Q在定直线上.
2021年六安市省示范高中高三教学质量检测
文科数学试题 答案
注意事项:
1.答题前,考生务必将自己的姓名、座位号等填写在答题卡和答题卷指定位置上.
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦于净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上,写在本试卷上无效
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知复数(i为虚数单位),则在复平面内对应的点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
【答案】D
2. 已知集合,,则( )
A. B. C. D.
【答案】C
3. 设,,则( )
A. B. C. D.
【答案】D
4. 已知命题,,则p是q的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】A
5. 已知函数的部分图象如图所示,则的解析式可能为( )
A. B.
C. D.
【答案】A
6. 已知,,C在抛物线上,且到焦点距离为5,则的面积为( )
A. 4 B. 5 C. 8 D. 10
【答案】A
7. 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为( )
A. B. C. D.
【答案】A
8. 六安市新建的广播电视发射塔计划于2021年3月竣工,它被誉为六安的“东方明珠塔”,是一个集发射和接收信号、应急指挥、旅游休闲于一体的多功能文化景观塔.发射塔总体高度308米,主要由塔座、塔身、塔楼、桅杆四部分组成.其塔身是双曲线的一部分绕其虚轴旋转所成的曲面(如图1),它的最小口径为2r米,在最小口径上方h米处的口径为4r米,若某同学在平面直角坐标系中绘制出了该双曲线(如图2),则其渐近线的方程为( )
A. B. C. D.
【答案】B
9. 设等差数列的前n项和为,公差且,则取得最小值时,n的值为( )
A. 3 B. 4 C. 3或4 D. 4或5
【答案】C
10. 《九章算术》是中国古代的数学专著,其中的“更相减损术”可以用来求两个数的最大公约数,这是一个伟大创举.其内容如下:“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也,以等数约之”.下面的程序框图体现了该算法的主要过程,若输入,,时,则输出的结果为( )
A. , B. ,
C. , D. ,
【答案】B
11. 已知,直线,P为l上的动点,过点Р作的切线PA,PB,切点为A,B,则最小值为( )
A. 1 B. C. 2 D.
【答案】C
12. 已知函数,.对于任意,且,都有,则实数a的取值范围是( )
A. B. C. D.
【答案】D
二、填空题:本题共4题,每小题5分,共20分.
13. 已知两个单位向量与夹角为,则__________.
【答案】
14. 若实数x,y满足,则的最大值为__________.
【答案】
15. 已知,为偶函数,若曲线在点处切线方程为,则__________.
【答案】3
16. 图,在中,,垂足为D,,垂足为E.现将沿AD折起,使得,若三棱锥外接球的球心为О,半径为1,则面积的最大值为___________.
【答案】
三、解答题:本题共6小题,共70分.解答须写出文字说明、证明过程和演算步骤.
17. 从下列①②③选项中,选择其中一个作为条件进行解答:
①已知数列的前n项和;
②已知数列是等比数列,,;
③已知数列中,,且对任意的正整数m,n都有.
(1)求数列的通项公式;
(2)已知,求数列的前2021项的和.
【答案】(1)条件选择见解析;;(2).
18. 已知函数.
(1)求函数的单调递增区间;
(2)将函数图象上所有点的横坐标缩短到原来的倍(纵坐标不变),再把图象向右平移个单位长度,得到函数的图象,当时,求函数的值域.
【答案】(1);(2).
19. 如图,在四棱锥中,平面ABCD.,,,E是PD的中点.
(1)证明:平面PBC;
(2)若,求三棱锥的体积.
【答案】(1)证明见解析;(2).
20. 为积极响应国家对垃圾分类处理的号召,增强市民的环保意识,加快城市生态文明的建设,某市决定在A,B,C三个社区进行垃圾分类回收试点,现准备建造一座垃圾处理站D,集中处理三个社区的湿垃圾.如图,已知千米,千米,,.
(1)求垃圾处理站D与社区A之间距离;
(2)假设有大、小两种运输车,负责在各社区和垃圾处理站之间运输湿垃圾,车在运输期间都是直线行驶,每辆大车的行车费用为每千米a元,每辆小车的行车费用为每千米元().
现有两种运输湿垃圾的方案
方案一:用一辆大车运输,从D出发,依次经A,B,C,再由C返回到D;
方案二:用三辆小车运输,均从D出发.分别到A,B,C,再各自原路返回到D.
请从行车费用的角度比较哪种方案更合算,并说明理由.
【答案】(1)2千米;(2)当时,方案一,方案二一样合算;当时,方案二合算;当时,方案一合算.
21. 已知函数,
(1)若,的极大值是,求a的值;
(2)若,在上存在唯一零点,求b的值.
【答案】(1);(2).
22. 已知椭圆的离心率为,短轴长为.
(1)求椭圆C的方程;
(2)设A,B分别为椭圆C的左、右顶点,若过点且斜率不为0的直线l与椭圆C交于M、N两点,直线AM与BN相交于点Q.证明:点Q在定直线上.
【答案】(1);(2)证明见解析.
文科数学试题
注意事项:
1.答题前,考生务必将自己的姓名、座位号等填写在答题卡和答题卷指定位置上.
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦于净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上,写在本试卷上无效
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知复数(i为虚数单位),则在复平面内对应的点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 已知集合,,则( )
A. B. C. D.
3. 设,,则( )
A. B. C. D.
4. 已知命题,,则p是q的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
5. 已知函数的部分图象如图所示,则的解析式可能为( )
A. B.
C. D.
6. 已知,,C在抛物线上,且到焦点距离为5,则的面积为( )
A. 4 B. 5 C. 8 D. 10
7. 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为( )
A. B. C. D.
8. 六安市新建的广播电视发射塔计划于2021年3月竣工,它被誉为六安的“东方明珠塔”,是一个集发射和接收信号、应急指挥、旅游休闲于一体的多功能文化景观塔.发射塔总体高度308米,主要由塔座、塔身、塔楼、桅杆四部分组成.其塔身是双曲线的一部分绕其虚轴旋转所成的曲面(如图1),它的最小口径为2r米,在最小口径上方h米处的口径为4r米,若某同学在平面直角坐标系中绘制出了该双曲线(如图2),则其渐近线的方程为( )
A. B. C. D.
9. 设等差数列的前n项和为,公差且,则取得最小值时,n的值为( )
A. 3 B. 4 C. 3或4 D. 4或5
10. 《九章算术》是中国古代的数学专著,其中的“更相减损术”可以用来求两个数的最大公约数,这是一个伟大创举.其内容如下:“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也,以等数约之”.下面的程序框图体现了该算法的主要过程,若输入,,时,则输出的结果为( )
A. , B. ,
C. , D. ,
11. 已知,直线,P为l上的动点,过点Р作的切线PA,PB,切点为A,B,则最小值为( )
A. 1 B. C. 2 D.
12. 已知函数,.对于任意,且,都有,则实数a的取值范围是( )
A. B. C. D.
二、填空题:本题共4题,每小题5分,共20分.
13. 已知两个单位向量与夹角为,则__________.
14. 若实数x,y满足,则的最大值为__________.
15. 已知,为偶函数,若曲线在点处切线方程为,则__________.
16. 图,在中,,垂足为D,,垂足为E.现将沿AD折起,使得,若三棱锥外接球的球心为О,半径为1,则面积的最大值为___________.
三、解答题:本题共6小题,共70分.解答须写出文字说明、证明过程和演算步骤.
17. 从下列①②③选项中,选择其中一个作为条件进行解答:
①已知数列的前n项和;
②已知数列是等比数列,,;
③已知数列中,,且对任意的正整数m,n都有.
(1)求数列的通项公式;
(2)已知,求数列的前2021项的和.
18. 已知函数.
(1)求函数的单调递增区间;
(2)将函数图象上所有点的横坐标缩短到原来的倍(纵坐标不变),再把图象向右平移个单位长度,得到函数的图象,当时,求函数的值域.
.
19. 如图,在四棱锥中,平面ABCD.,,,E是PD的中点.
(1)证明:平面PBC;
(2)若,求三棱锥的体积.
20. 为积极响应国家对垃圾分类处理的号召,增强市民的环保意识,加快城市生态文明的建设,某市决定在A,B,C三个社区进行垃圾分类回收试点,现准备建造一座垃圾处理站D,集中处理三个社区的湿垃圾.如图,已知千米,千米,,.
(1)求垃圾处理站D与社区A之间距离;
(2)假设有大、小两种运输车,负责在各社区和垃圾处理站之间运输湿垃圾,车在运输期间都是直线行驶,每辆大车的行车费用为每千米a元,每辆小车的行车费用为每千米元().
现有两种运输湿垃圾的方案
方案一:用一辆大车运输,从D出发,依次经A,B,C,再由C返回到D;
方案二:用三辆小车运输,均从D出发.分别到A,B,C,再各自原路返回到D.
请从行车费用的角度比较哪种方案更合算,并说明理由.
21. 已知函数,
(1)若,的极大值是,求a的值;
(2)若,在上存在唯一零点,求b的值.
22. 已知椭圆的离心率为,短轴长为.
(1)求椭圆C的方程;
(2)设A,B分别为椭圆C的左、右顶点,若过点且斜率不为0的直线l与椭圆C交于M、N两点,直线AM与BN相交于点Q.证明:点Q在定直线上.
2021年六安市省示范高中高三教学质量检测
文科数学试题 答案
注意事项:
1.答题前,考生务必将自己的姓名、座位号等填写在答题卡和答题卷指定位置上.
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦于净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上,写在本试卷上无效
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知复数(i为虚数单位),则在复平面内对应的点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
【答案】D
2. 已知集合,,则( )
A. B. C. D.
【答案】C
3. 设,,则( )
A. B. C. D.
【答案】D
4. 已知命题,,则p是q的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】A
5. 已知函数的部分图象如图所示,则的解析式可能为( )
A. B.
C. D.
【答案】A
6. 已知,,C在抛物线上,且到焦点距离为5,则的面积为( )
A. 4 B. 5 C. 8 D. 10
【答案】A
7. 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为( )
A. B. C. D.
【答案】A
8. 六安市新建的广播电视发射塔计划于2021年3月竣工,它被誉为六安的“东方明珠塔”,是一个集发射和接收信号、应急指挥、旅游休闲于一体的多功能文化景观塔.发射塔总体高度308米,主要由塔座、塔身、塔楼、桅杆四部分组成.其塔身是双曲线的一部分绕其虚轴旋转所成的曲面(如图1),它的最小口径为2r米,在最小口径上方h米处的口径为4r米,若某同学在平面直角坐标系中绘制出了该双曲线(如图2),则其渐近线的方程为( )
A. B. C. D.
【答案】B
9. 设等差数列的前n项和为,公差且,则取得最小值时,n的值为( )
A. 3 B. 4 C. 3或4 D. 4或5
【答案】C
10. 《九章算术》是中国古代的数学专著,其中的“更相减损术”可以用来求两个数的最大公约数,这是一个伟大创举.其内容如下:“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也,以等数约之”.下面的程序框图体现了该算法的主要过程,若输入,,时,则输出的结果为( )
A. , B. ,
C. , D. ,
【答案】B
11. 已知,直线,P为l上的动点,过点Р作的切线PA,PB,切点为A,B,则最小值为( )
A. 1 B. C. 2 D.
【答案】C
12. 已知函数,.对于任意,且,都有,则实数a的取值范围是( )
A. B. C. D.
【答案】D
二、填空题:本题共4题,每小题5分,共20分.
13. 已知两个单位向量与夹角为,则__________.
【答案】
14. 若实数x,y满足,则的最大值为__________.
【答案】
15. 已知,为偶函数,若曲线在点处切线方程为,则__________.
【答案】3
16. 图,在中,,垂足为D,,垂足为E.现将沿AD折起,使得,若三棱锥外接球的球心为О,半径为1,则面积的最大值为___________.
【答案】
三、解答题:本题共6小题,共70分.解答须写出文字说明、证明过程和演算步骤.
17. 从下列①②③选项中,选择其中一个作为条件进行解答:
①已知数列的前n项和;
②已知数列是等比数列,,;
③已知数列中,,且对任意的正整数m,n都有.
(1)求数列的通项公式;
(2)已知,求数列的前2021项的和.
【答案】(1)条件选择见解析;;(2).
18. 已知函数.
(1)求函数的单调递增区间;
(2)将函数图象上所有点的横坐标缩短到原来的倍(纵坐标不变),再把图象向右平移个单位长度,得到函数的图象,当时,求函数的值域.
【答案】(1);(2).
19. 如图,在四棱锥中,平面ABCD.,,,E是PD的中点.
(1)证明:平面PBC;
(2)若,求三棱锥的体积.
【答案】(1)证明见解析;(2).
20. 为积极响应国家对垃圾分类处理的号召,增强市民的环保意识,加快城市生态文明的建设,某市决定在A,B,C三个社区进行垃圾分类回收试点,现准备建造一座垃圾处理站D,集中处理三个社区的湿垃圾.如图,已知千米,千米,,.
(1)求垃圾处理站D与社区A之间距离;
(2)假设有大、小两种运输车,负责在各社区和垃圾处理站之间运输湿垃圾,车在运输期间都是直线行驶,每辆大车的行车费用为每千米a元,每辆小车的行车费用为每千米元().
现有两种运输湿垃圾的方案
方案一:用一辆大车运输,从D出发,依次经A,B,C,再由C返回到D;
方案二:用三辆小车运输,均从D出发.分别到A,B,C,再各自原路返回到D.
请从行车费用的角度比较哪种方案更合算,并说明理由.
【答案】(1)2千米;(2)当时,方案一,方案二一样合算;当时,方案二合算;当时,方案一合算.
21. 已知函数,
(1)若,的极大值是,求a的值;
(2)若,在上存在唯一零点,求b的值.
【答案】(1);(2).
22. 已知椭圆的离心率为,短轴长为.
(1)求椭圆C的方程;
(2)设A,B分别为椭圆C的左、右顶点,若过点且斜率不为0的直线l与椭圆C交于M、N两点,直线AM与BN相交于点Q.证明:点Q在定直线上.
【答案】(1);(2)证明见解析.
同课章节目录
