安徽省六安市示范高中2021届高三上学期期末教学质量检测数学(理)试题 Word版含答案
文档属性
| 名称 | 安徽省六安市示范高中2021届高三上学期期末教学质量检测数学(理)试题 Word版含答案 |

|
|
| 格式 | doc | ||
| 文件大小 | 973.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-20 00:00:00 | ||
图片预览




文档简介
2021年六安市省示范高中高三教学质量检测
理科数学试题
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知复数(为虚数单位),则在复平面内对应的点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 已知集合,,则( )
A. B. C. D.
3. 若平面向量与的夹角为,,,则( )
A. B. C. 18 D. 12
4. 已知函数的部分图象如图所示,则的解析式可能为( )
A. B.
C. D.
5. 设,,,则( )
A. B. C. D.
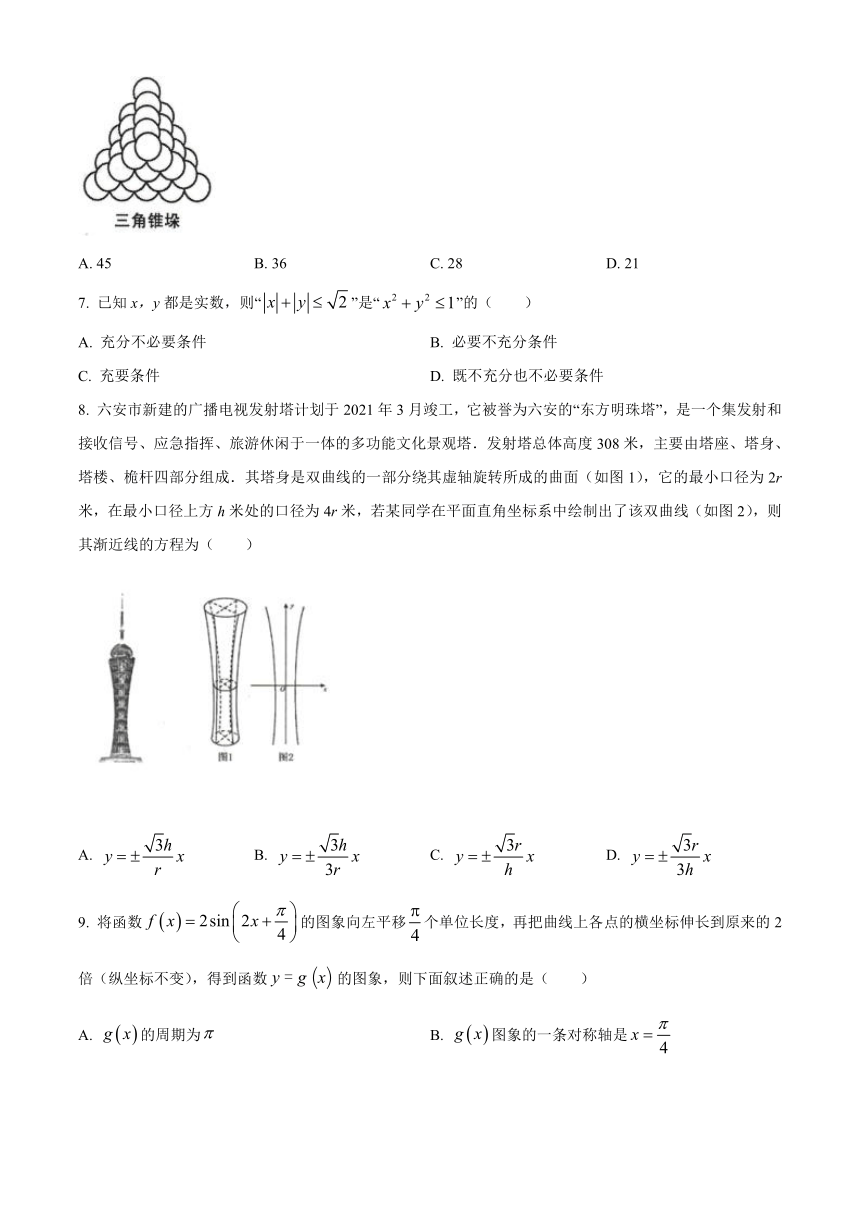
6. “垛积术”是我国古代数学重要成就之一,宋元时期数学家朱世杰在《四元玉鉴》中记载了“三角形垛”,其中的“落一形”堆垛就是每层为“三角形数”的三角锥的堆垛(俯视如图所示,顶上一层1个球,下一层3个球,再下一层6个球,…).若一“落一形”三角锥垛有6层,则该堆垛第6层的小球个数为( )
A. 45 B. 36 C. 28 D. 21
7. 已知x,y都是实数,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
8. 六安市新建的广播电视发射塔计划于2021年3月竣工,它被誉为六安的“东方明珠塔”,是一个集发射和接收信号、应急指挥、旅游休闲于一体的多功能文化景观塔.发射塔总体高度308米,主要由塔座、塔身、塔楼、桅杆四部分组成.其塔身是双曲线的一部分绕其虚轴旋转所成的曲面(如图1),它的最小口径为2r米,在最小口径上方h米处的口径为4r米,若某同学在平面直角坐标系中绘制出了该双曲线(如图2),则其渐近线的方程为( )
A. B. C. D.
9. 将函数的图象向左平移个单位长度,再把曲线上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数的图象,则下面叙述正确的是( )
A. 的周期为 B. 图象的一条对称轴是
C. 图象的一个对称中心为 D. 在上单调递减
10. 已知圆,过直线在第一象限内一动点P作圆O的两条切线,切点分别是A,B,直线AB与两坐标轴分别交于M,N两点,则面积的最小值为( )
A. B. 1 C. D. 2
11. 在棱长为1正方体中,E为棱CD上的动点(不含端点),过B,E,的截面与棱交于F,若截面在平面和平面上正投影的周长分别为,,则( )
A. 有最小值 B. 有最大值
C. 是定值 D. 是定值
12. 已知函数(其中e为自然对数的底数)有三个零点,则实数m的取值范围为( )
A. B.
C. D.
二、填空题:本题共4小题,每小题5分,共20分.
13. 若实数x,y满足,则的最大值为__________.
14. 已知,为偶函数,若曲线在点处的切线方程为,则__________.
15. 已知抛物线,F为焦点,直线与C交于A点,B为直线l上另一点(在A点上方),则角平分线所在直线方程为_____________.
16. 已知三棱锥,底面是边长为2的正三角形,平面平面ABC.,M为棱PC上一点,且,过M作三棱锥外接球的截面,则截面面积最小值为____________.
三、解答题:本题共6小题,共70分解答题应写出文字说明、证明过程和演算步骤.
17. 已知数列的前n项和为,且满足.
(1)求数列的通项公式;
(2)若,求数列前n项和.
.
18. 在中,角A,B,C所对的边分别为a,b,c,且.
(1)求角B的大小;
(2)若 ,,求的面积.
19. 如图,在平面四边形中,,,,,现把沿折起,使在平面上的射影为,连接、,且.
(1)证明:平面;
(2)求二面角的余弦值.
20. 已知函数,
(1)若,的极大值是,求a的值;
(2)若,在上存在唯一零点,求b的值.
.
21. 已知椭圆的离心率为,短轴长为.
(1)求椭圆C的方程;
(2)设不经过点且斜率存在的直线l与椭圆C交于M,N两点,直线PM与PN的斜率之和为,证明:直线l过定点.
22. 已知函数.
(1)若,求的单调区间;
(2)若在上有两个极值点, .
(i)求实数a的取值范围;
(ii)求证:.
2021年六安市省示范高中高三教学质量检测
理科数学试题 答案
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知复数(为虚数单位),则在复平面内对应的点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
【答案】D
2. 已知集合,,则( )
A. B. C. D.
【答案】C
3. 若平面向量与的夹角为,,,则( )
A. B. C. 18 D. 12
【答案】B
4. 已知函数的部分图象如图所示,则的解析式可能为( )
A. B.
C. D.
【答案】A
5. 设,,,则( )
A. B. C. D.
【答案】C
6. “垛积术”是我国古代数学重要成就之一,宋元时期数学家朱世杰在《四元玉鉴》中记载了“三角形垛”,其中的“落一形”堆垛就是每层为“三角形数”的三角锥的堆垛(俯视如图所示,顶上一层1个球,下一层3个球,再下一层6个球,…).若一“落一形”三角锥垛有6层,则该堆垛第6层的小球个数为( )
A. 45 B. 36 C. 28 D. 21
【答案】D
7. 已知x,y都是实数,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】B
8. 六安市新建的广播电视发射塔计划于2021年3月竣工,它被誉为六安的“东方明珠塔”,是一个集发射和接收信号、应急指挥、旅游休闲于一体的多功能文化景观塔.发射塔总体高度308米,主要由塔座、塔身、塔楼、桅杆四部分组成.其塔身是双曲线的一部分绕其虚轴旋转所成的曲面(如图1),它的最小口径为2r米,在最小口径上方h米处的口径为4r米,若某同学在平面直角坐标系中绘制出了该双曲线(如图2),则其渐近线的方程为( )
A. B. C. D.
【答案】B
9. 将函数的图象向左平移个单位长度,再把曲线上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数的图象,则下面叙述正确的是( )
A. 的周期为 B. 图象的一条对称轴是
C. 图象的一个对称中心为 D. 在上单调递减
【答案】D
10. 已知圆,过直线在第一象限内一动点P作圆O的两条切线,切点分别是A,B,直线AB与两坐标轴分别交于M,N两点,则面积的最小值为( )
A. B. 1 C. D. 2
【答案】B
11. 在棱长为1正方体中,E为棱CD上的动点(不含端点),过B,E,的截面与棱交于F,若截面在平面和平面上正投影的周长分别为,,则( )
A. 有最小值 B. 有最大值
C. 是定值 D. 是定值
【答案】A
12. 已知函数(其中e为自然对数的底数)有三个零点,则实数m的取值范围为( )
A. B.
C. D.
【答案】C
二、填空题:本题共4小题,每小题5分,共20分.
13. 若实数x,y满足,则的最大值为__________.
【答案】
14. 已知,为偶函数,若曲线在点处的切线方程为,则__________.
【答案】3
15. 已知抛物线,F为焦点,直线与C交于A点,B为直线l上另一点(在A点上方),则角平分线所在直线方程为_____________.
【答案】
16. 已知三棱锥,底面是边长为2的正三角形,平面平面ABC.,M为棱PC上一点,且,过M作三棱锥外接球的截面,则截面面积最小值为____________.
【答案】
三、解答题:本题共6小题,共70分解答题应写出文字说明、证明过程和演算步骤.
17. 已知数列的前n项和为,且满足.
(1)求数列的通项公式;
(2)若,求数列前n项和.
【答案】(1);(2).
18. 在中,角A,B,C所对的边分别为a,b,c,且.
(1)求角B的大小;
(2)若 ,,求的面积.
【答案】(1);(2).
19. 如图,在平面四边形中,,,,,现把沿折起,使在平面上的射影为,连接、,且.
(1)证明:平面;
(2)求二面角的余弦值.
【答案】(1)证明见解析;(2).
20. 已知函数,
(1)若,的极大值是,求a的值;
(2)若,在上存在唯一零点,求b的值.
【答案】(1);(2).
21. 已知椭圆的离心率为,短轴长为.
(1)求椭圆C的方程;
(2)设不经过点且斜率存在的直线l与椭圆C交于M,N两点,直线PM与PN的斜率之和为,证明:直线l过定点.
【答案】(1);(2)证明见解析
22. 已知函数.
(1)若,求的单调区间;
(2)若在上有两个极值点, .
(i)求实数a的取值范围;
(ii)求证:.
【答案】(1)递减区间,递增区间为;(2)(i),(ii)证明见解析.
理科数学试题
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知复数(为虚数单位),则在复平面内对应的点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 已知集合,,则( )
A. B. C. D.
3. 若平面向量与的夹角为,,,则( )
A. B. C. 18 D. 12
4. 已知函数的部分图象如图所示,则的解析式可能为( )
A. B.
C. D.
5. 设,,,则( )
A. B. C. D.
6. “垛积术”是我国古代数学重要成就之一,宋元时期数学家朱世杰在《四元玉鉴》中记载了“三角形垛”,其中的“落一形”堆垛就是每层为“三角形数”的三角锥的堆垛(俯视如图所示,顶上一层1个球,下一层3个球,再下一层6个球,…).若一“落一形”三角锥垛有6层,则该堆垛第6层的小球个数为( )
A. 45 B. 36 C. 28 D. 21
7. 已知x,y都是实数,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
8. 六安市新建的广播电视发射塔计划于2021年3月竣工,它被誉为六安的“东方明珠塔”,是一个集发射和接收信号、应急指挥、旅游休闲于一体的多功能文化景观塔.发射塔总体高度308米,主要由塔座、塔身、塔楼、桅杆四部分组成.其塔身是双曲线的一部分绕其虚轴旋转所成的曲面(如图1),它的最小口径为2r米,在最小口径上方h米处的口径为4r米,若某同学在平面直角坐标系中绘制出了该双曲线(如图2),则其渐近线的方程为( )
A. B. C. D.
9. 将函数的图象向左平移个单位长度,再把曲线上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数的图象,则下面叙述正确的是( )
A. 的周期为 B. 图象的一条对称轴是
C. 图象的一个对称中心为 D. 在上单调递减
10. 已知圆,过直线在第一象限内一动点P作圆O的两条切线,切点分别是A,B,直线AB与两坐标轴分别交于M,N两点,则面积的最小值为( )
A. B. 1 C. D. 2
11. 在棱长为1正方体中,E为棱CD上的动点(不含端点),过B,E,的截面与棱交于F,若截面在平面和平面上正投影的周长分别为,,则( )
A. 有最小值 B. 有最大值
C. 是定值 D. 是定值
12. 已知函数(其中e为自然对数的底数)有三个零点,则实数m的取值范围为( )
A. B.
C. D.
二、填空题:本题共4小题,每小题5分,共20分.
13. 若实数x,y满足,则的最大值为__________.
14. 已知,为偶函数,若曲线在点处的切线方程为,则__________.
15. 已知抛物线,F为焦点,直线与C交于A点,B为直线l上另一点(在A点上方),则角平分线所在直线方程为_____________.
16. 已知三棱锥,底面是边长为2的正三角形,平面平面ABC.,M为棱PC上一点,且,过M作三棱锥外接球的截面,则截面面积最小值为____________.
三、解答题:本题共6小题,共70分解答题应写出文字说明、证明过程和演算步骤.
17. 已知数列的前n项和为,且满足.
(1)求数列的通项公式;
(2)若,求数列前n项和.
.
18. 在中,角A,B,C所对的边分别为a,b,c,且.
(1)求角B的大小;
(2)若 ,,求的面积.
19. 如图,在平面四边形中,,,,,现把沿折起,使在平面上的射影为,连接、,且.
(1)证明:平面;
(2)求二面角的余弦值.
20. 已知函数,
(1)若,的极大值是,求a的值;
(2)若,在上存在唯一零点,求b的值.
.
21. 已知椭圆的离心率为,短轴长为.
(1)求椭圆C的方程;
(2)设不经过点且斜率存在的直线l与椭圆C交于M,N两点,直线PM与PN的斜率之和为,证明:直线l过定点.
22. 已知函数.
(1)若,求的单调区间;
(2)若在上有两个极值点, .
(i)求实数a的取值范围;
(ii)求证:.
2021年六安市省示范高中高三教学质量检测
理科数学试题 答案
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知复数(为虚数单位),则在复平面内对应的点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
【答案】D
2. 已知集合,,则( )
A. B. C. D.
【答案】C
3. 若平面向量与的夹角为,,,则( )
A. B. C. 18 D. 12
【答案】B
4. 已知函数的部分图象如图所示,则的解析式可能为( )
A. B.
C. D.
【答案】A
5. 设,,,则( )
A. B. C. D.
【答案】C
6. “垛积术”是我国古代数学重要成就之一,宋元时期数学家朱世杰在《四元玉鉴》中记载了“三角形垛”,其中的“落一形”堆垛就是每层为“三角形数”的三角锥的堆垛(俯视如图所示,顶上一层1个球,下一层3个球,再下一层6个球,…).若一“落一形”三角锥垛有6层,则该堆垛第6层的小球个数为( )
A. 45 B. 36 C. 28 D. 21
【答案】D
7. 已知x,y都是实数,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】B
8. 六安市新建的广播电视发射塔计划于2021年3月竣工,它被誉为六安的“东方明珠塔”,是一个集发射和接收信号、应急指挥、旅游休闲于一体的多功能文化景观塔.发射塔总体高度308米,主要由塔座、塔身、塔楼、桅杆四部分组成.其塔身是双曲线的一部分绕其虚轴旋转所成的曲面(如图1),它的最小口径为2r米,在最小口径上方h米处的口径为4r米,若某同学在平面直角坐标系中绘制出了该双曲线(如图2),则其渐近线的方程为( )
A. B. C. D.
【答案】B
9. 将函数的图象向左平移个单位长度,再把曲线上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数的图象,则下面叙述正确的是( )
A. 的周期为 B. 图象的一条对称轴是
C. 图象的一个对称中心为 D. 在上单调递减
【答案】D
10. 已知圆,过直线在第一象限内一动点P作圆O的两条切线,切点分别是A,B,直线AB与两坐标轴分别交于M,N两点,则面积的最小值为( )
A. B. 1 C. D. 2
【答案】B
11. 在棱长为1正方体中,E为棱CD上的动点(不含端点),过B,E,的截面与棱交于F,若截面在平面和平面上正投影的周长分别为,,则( )
A. 有最小值 B. 有最大值
C. 是定值 D. 是定值
【答案】A
12. 已知函数(其中e为自然对数的底数)有三个零点,则实数m的取值范围为( )
A. B.
C. D.
【答案】C
二、填空题:本题共4小题,每小题5分,共20分.
13. 若实数x,y满足,则的最大值为__________.
【答案】
14. 已知,为偶函数,若曲线在点处的切线方程为,则__________.
【答案】3
15. 已知抛物线,F为焦点,直线与C交于A点,B为直线l上另一点(在A点上方),则角平分线所在直线方程为_____________.
【答案】
16. 已知三棱锥,底面是边长为2的正三角形,平面平面ABC.,M为棱PC上一点,且,过M作三棱锥外接球的截面,则截面面积最小值为____________.
【答案】
三、解答题:本题共6小题,共70分解答题应写出文字说明、证明过程和演算步骤.
17. 已知数列的前n项和为,且满足.
(1)求数列的通项公式;
(2)若,求数列前n项和.
【答案】(1);(2).
18. 在中,角A,B,C所对的边分别为a,b,c,且.
(1)求角B的大小;
(2)若 ,,求的面积.
【答案】(1);(2).
19. 如图,在平面四边形中,,,,,现把沿折起,使在平面上的射影为,连接、,且.
(1)证明:平面;
(2)求二面角的余弦值.
【答案】(1)证明见解析;(2).
20. 已知函数,
(1)若,的极大值是,求a的值;
(2)若,在上存在唯一零点,求b的值.
【答案】(1);(2).
21. 已知椭圆的离心率为,短轴长为.
(1)求椭圆C的方程;
(2)设不经过点且斜率存在的直线l与椭圆C交于M,N两点,直线PM与PN的斜率之和为,证明:直线l过定点.
【答案】(1);(2)证明见解析
22. 已知函数.
(1)若,求的单调区间;
(2)若在上有两个极值点, .
(i)求实数a的取值范围;
(ii)求证:.
【答案】(1)递减区间,递增区间为;(2)(i),(ii)证明见解析.
同课章节目录
