2020-2021学年九年级数学人教版下册第27章 《相似 》章节培优训练(五)(Word版 含答案)
文档属性
| 名称 | 2020-2021学年九年级数学人教版下册第27章 《相似 》章节培优训练(五)(Word版 含答案) | 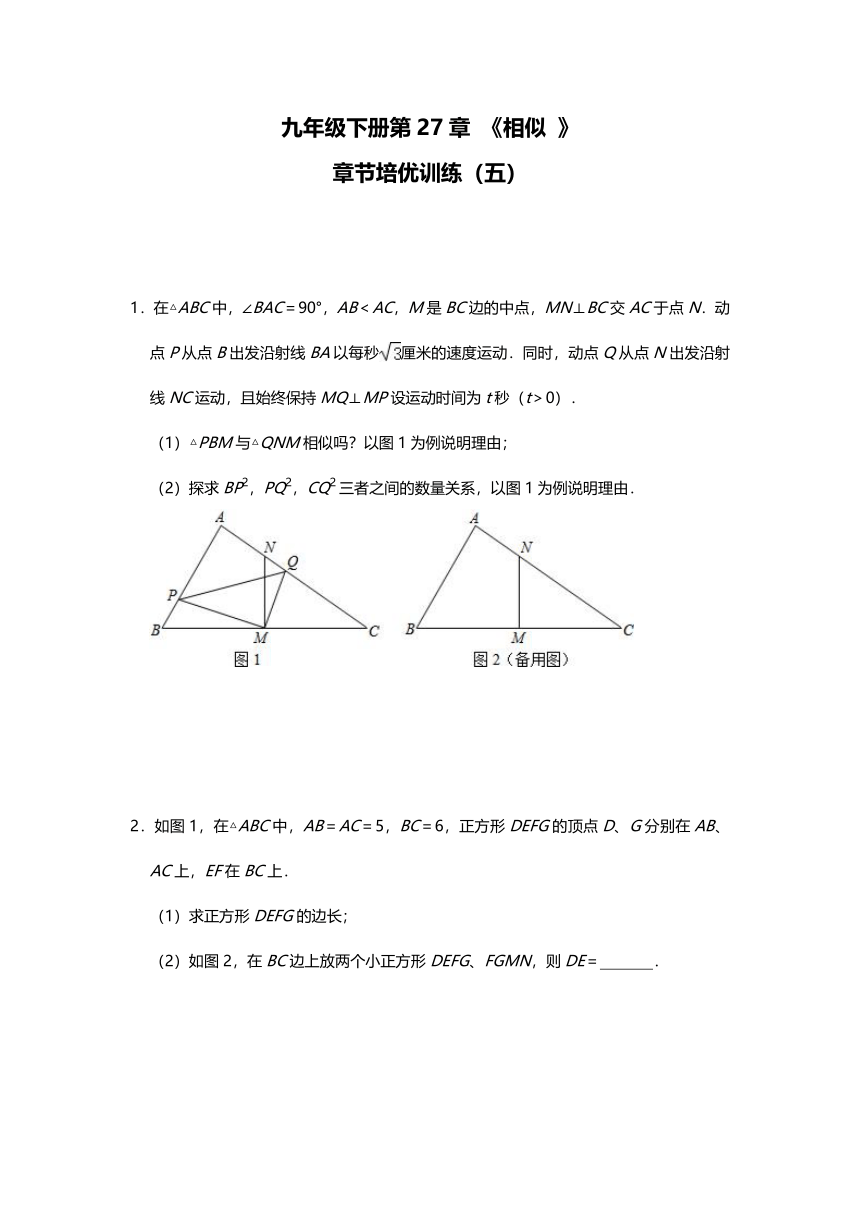 | |
| 格式 | zip | ||
| 文件大小 | 189.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 09:38:01 | ||
图片预览





文档简介
九年级下册第27章
《相似
》
章节培优训练(五)
1.在△ABC中,∠BAC=90°,AB<AC,M是BC边的中点,MN⊥BC交AC于点N.动点P从点B出发沿射线BA以每秒厘米的速度运动.同时,动点Q从点N出发沿射线NC运动,且始终保持MQ⊥MP设运动时间为t秒(t>0).
(1)△PBM与△QNM相似吗?以图1为例说明理由;
(2)探求BP2,PQ2,CQ2三者之间的数量关系,以图1为例说明理由.
2.如图1,在△ABC中,AB=AC=5,BC=6,正方形DEFG的顶点D、G分别在AB、AC上,EF在BC上.
(1)求正方形DEFG的边长;
(2)如图2,在BC边上放两个小正方形DEFG、FGMN,则DE=
.
3.为了测量校园水平地面上一棵树的高度,数学兴趣小组利用一根标杆、皮尺,设计如图所示的测量方案.已知测量同学眼睛A、标杆顶端F、树的顶端E在同一直线上,此同学眼睛距地面1.6米,标杆高为3.2米,且BC=2米,CD=6米,求树ED的高.
4.如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD.连接MF,NF.试说明:
(1)∠MBN=45°;
(2)△MFN∽△BDC.
5.在△ABC中,已知边BC=12,该边上的高线AD=8,同样大小的两个正方形FMNG与EFGH按如图所示方式叠放,其中顶点M、N在BC边上,E、H分别在AB、AC上,求正方形的边长.
6.在△ABC中,AB=AC,D为BC的中点,点E在AB上,点F在AC上,ED平分∠BEF,连接DF.
(1)如图1,求证:∠EDF+∠A=90°;
(2)如图2,当∠ABC=45°时,点P在DE上,连接AP、CP交DF于点Q且满足∠APC=90°,若AE:BE=1:3,请你探究线段FQ与FC之间的数量关系,并证明你的结论.
7.如图,在△ABC中,点Q,M在BC上,点P,N分别在AB,AC上,边BC=120毫米,高AD=80毫米,四边形PQMN为矩形,设△ABC的高AD与PN相交于点E.
(1)若这个矩形是正方形,则边长是多少?
(2)若这个矩形的长是宽的2倍,则长和宽各是多少?
8.如图,用下面的方法可以画△AOB的内接等边三角形,阅读后解答相应问题.
画法:①在△AOB内画等边三角形CDE,使点C在OA上,点D在OB上;②连接OE并延长,交AB于点E′,过点E′作E′C′∥EC,交OA于点C′,作E′D′∥ED,交OB于点D′;③连接C′D′,则△C′D′E′是△AOB的内接等边三角形.
(1)求证:△C′D′E′是等边三角形;
(2)求作:内接于已知△ABC的矩形DEFG,使它的边EF在BC上,顶点D,G分别在AB,AC上,且DE:EF=1:2.
9.如图,A,B两个村子在一条河的同侧,A,B两村到河岸的距离分别为AC=1km,BD=3km,其中CD=3km.现在要在河岸CD上建一个水厂,向A,B两个村庄输送自来水,请你在CD上选择水厂的位置O,使铺设的水管总长度最小?
10.如图,在△ABC中,AC=BC,F为边AB上的一点,BF:AF=m:n(m、n>0),取CF的中点D,连结AD并延长交BC于点E.
(1)求BE:EC的值;
(2)若BE=2EC,那么CF所在的直线与边AB有怎样的位置关系?证明你的结论.
(3)E点能否成为BC中点?若能,求出相应的m:n,若不能,证明你的结论.
参考答案
1.解:(1)△PBM∽△QNM.理由如下:
如图1,∵MQ⊥MP,MN⊥BC(已知),
∴∠PMB+∠PMN=90°,∠QMN+∠PMN=90°,
∴∠PMB=∠QMN(等量代换).
∵∠PBM+∠C=90°(直角三角形的两个锐角互余),∠QNM+∠C=90°(直角三角形的两个锐角互余),
∴∠PBM=∠QNM(等量代换).
∴△PBM∽△QNM;
(2)PQ2=BP2+CQ2.
证明如下:如图1,延长QM至点D,使MD=MQ.连接PD、BD,BQ,CD
∵BC、DQ互相平分,
∴四边形BDCQ为平行四边形,
∴BD∥CQ,BD=CQ(平行四边形的对边平行且相等);
又∵∠BAC=90°,
∴∠PBD=90°,
∴PD2=BP2+BD2=BP2+CQ2,
∵PM垂直平分DQ,
∴PQ=PD,
∴PQ2=BP2+CQ2.
2.解:过点作AM⊥BC于点M,
∵AB=AC=5,BC=6,
∴BM=BC=3,
在Rt△ABM中,AM==4,
∵四边形DEFG是矩形,
∴DG∥EF,DE⊥BC,
∴AN⊥DG,四边形EDMN是矩形,
∴MN=DE,
设MN=DE=x,
∵DG∥EF,
∴△ADG∽△ABC,
∴DG:BC=AN:AM,
∴,
解得:DG=﹣x+6,
∵四边形DEFG为正方形,
∴DE=DG,即x=﹣x+6,
解得x=,
∴正方形DEFG的边长为;
(2)由题意得:DN=2DE,
由(1)知:,
∴DE=.
故答案为:.
3.解:如图,过A作AH垂直ED,垂足为H,交线段FC与G,
由题知,∵FG∥EH,
∴△AFG∽△AEH,
∴=,
又因为AG=BC=2,AH=BD=2+6=8,FG=FC﹣GC=3.2﹣1.6=1.6,
所以=,
解得:EH=6.4,
则ED=EH+HD=6.4+1.6=8(m).
答:树ED的高为8米.
4.证明:(1)∵AB=AC,点M是BC的中点,
∴AM⊥BC,AM平分∠BAC,
∵BN平分∠ABE,
∴∠EBN=∠ABN,
∵AC⊥BD,
∴∠AEB=90°,
∴∠EAB+∠EBA=90°,
∴∠MNB=∠NAB+∠ABN=(∠EAB+∠EBA)=45°,
∴∠MBN=45°;
(2)∵点F,M分别是AB,BC的中点,
∴FM∥AC,FM=AC,
∵AC=BD,
∴FM=BD,即=,
由(1)知△BMN是等腰直角三角形,
∴MN=BM=BC,即=,
∴=,
∵AM⊥BC,
∴∠NMF+∠FMB=90°,
∵FM∥AC,
∴∠ACB=∠FMB,
∵∠CEB=90°,
∴∠ACB+∠CBD=90°,
∴∠CBD+∠FMB=90°,
∴∠NMF=∠CBD,
∴△MFN∽△BDC.
5.解:设正方形EFGH的边长HG=x,
∵EH∥BC,
∴△AEH∽△ABC,
∴=,
解得,x=3,
答:正方形的边长为3.
6.证明:(1)连接AD,过D作DM⊥AB于M,DN⊥EF于N,DK⊥AC于K,
∵AB=AC,
∴AD平分∠BAC,
∴DM=DK,
∵ED平分∠BEF,
∴DM=DN,
∴DM=DN=DK,
∴DF平分∠EFC,
∵∠AEF+∠AFE=180°﹣∠A,
∴∠DEF+∠DFE=[360°﹣(∠AEF+∠AFE)]=180°﹣(180°﹣∠A)=90°+A,
∴∠EDF=90°﹣∠A,
∴∠EDF+∠A=90°;
(2)连接AD,过D作DM⊥AB于M,DN⊥AC于N,过E作EK⊥AD于K,
∵AB=AC,
∴∠ABC=∠ACB=45°,
∴∠BAC=90°,
∵D为BC的中点,
∴∠BAD=∠CAD,
∴DM=DN,
∴四边形AMDN是正方形,AM=AB,
∵AE:BE=1:3,
∴AE=AB,
∴AE=EM,由(1)证得∠EDF+∠A=90°,
∵∠BAC=90°,
∴∠EDF=45°,
∵∠ADN=45°,
∴∠3=∠2,
∵∠APC=∠ADC=90°,
∴A,P,D,C四点共圆,
∴∠1=∠3,∠DPC=∠DAC=45°,
∴DF⊥PC,∴∠1=∠2=∠3,
∴sin∠1=sin∠3,
即=,
设EK=AK=a,则AE=a,AM=2a,AD=4a,
∴KD=3a,ED=a,
∴==.
7.解:(1)设正方形的边长为x毫米,
∵四边形PQMN为正方形,
∴PN∥QM,
∴△APN∽△ABC,
∴,即,
解得x=48,
∴正方形的边长是48mm;
(2)设长方形的宽为y毫米,由(1)得△APN∽△ABC,
∴,即,或,
解得y=30或y=,
∴长方形的宽为30mm,长为60mm或宽为
mm,长为
mm.
8.(1)证明:∵E′C′∥EC,E′D′∥ED,
∴△OCE∽△OC′E′,△ODE∽△OD′E′,
∴CE:C′E′=OE:OE′,DE:D′E′=OE:OE′,∠CEO=∠C′E′O,∠DEO=∠D′E′O,
∴CE:C′E′=DE:D′E′,∠CED=∠C′E′D′,
∴△CDE∽△C′D′E′,
∵△CDE是等边三角形,
∴△C′D′E′是等边三角形;
(2)解:画法:①在△ABC内画矩形D′E′F′G′,使点D′在AB上,点G′在AC上,且D′E′:D′G′=1:2;
②连接AE′并延长,交BC于点E,连接AF′并延长交BC于点F,过点E作ED∥E′D′交AB于点D,过点F作FG∥F′G′,交AC于点G;
③连接DG,则矩形DEFG是△ABC的内接四边形.
9.解:作点A关于CD的对称点E,连结BE交CD于点O,如图,
∵点A关于CD的对称点E,
∴OA=OE,AC=CE=1,
∴OA+OB=OE+OB=BE,
∴此时点O使OA+OB最小,
设OC=xkm,则OD=(3﹣x)km,
∵CE∥BD,
∴△ECO∽△BDO,
∴=,即=,解得x=0.75(km).
答:在CD上选择在离C处0.75km的地方建水厂,使铺设的水管总长度最小.
10.解:(1)如图,过点F作FG∥BC交AE于G,
则∠DFG=∠DCE,∠DGF=∠DEC,
∵D是CF的中点,
∴CD=DF,
在△DCE和△DFG中,
,
∴△DCE≌△DFG(ASA),
∴EC=GF,
∵BF:AF=m:n,
∴=,
∵FG∥BC,
∴△AFG∽△ABE,
∴==,
∴BE:EC=;
(2)若BE=2EC,则BE:EC=2,
由(1)知,=2,
解得m=n,
∴点F是AB的中点,
∵AC=BC,
∴CF⊥AB;
(3)不能.
理由如下:假设点E能成为BC中点,
则BE=EC,
∴BE:EC=1,
由(1)知=1,
解得m=0,
这与m、n>0相矛盾,
所以,点E不能成为BC中点.
《相似
》
章节培优训练(五)
1.在△ABC中,∠BAC=90°,AB<AC,M是BC边的中点,MN⊥BC交AC于点N.动点P从点B出发沿射线BA以每秒厘米的速度运动.同时,动点Q从点N出发沿射线NC运动,且始终保持MQ⊥MP设运动时间为t秒(t>0).
(1)△PBM与△QNM相似吗?以图1为例说明理由;
(2)探求BP2,PQ2,CQ2三者之间的数量关系,以图1为例说明理由.
2.如图1,在△ABC中,AB=AC=5,BC=6,正方形DEFG的顶点D、G分别在AB、AC上,EF在BC上.
(1)求正方形DEFG的边长;
(2)如图2,在BC边上放两个小正方形DEFG、FGMN,则DE=
.
3.为了测量校园水平地面上一棵树的高度,数学兴趣小组利用一根标杆、皮尺,设计如图所示的测量方案.已知测量同学眼睛A、标杆顶端F、树的顶端E在同一直线上,此同学眼睛距地面1.6米,标杆高为3.2米,且BC=2米,CD=6米,求树ED的高.
4.如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD.连接MF,NF.试说明:
(1)∠MBN=45°;
(2)△MFN∽△BDC.
5.在△ABC中,已知边BC=12,该边上的高线AD=8,同样大小的两个正方形FMNG与EFGH按如图所示方式叠放,其中顶点M、N在BC边上,E、H分别在AB、AC上,求正方形的边长.
6.在△ABC中,AB=AC,D为BC的中点,点E在AB上,点F在AC上,ED平分∠BEF,连接DF.
(1)如图1,求证:∠EDF+∠A=90°;
(2)如图2,当∠ABC=45°时,点P在DE上,连接AP、CP交DF于点Q且满足∠APC=90°,若AE:BE=1:3,请你探究线段FQ与FC之间的数量关系,并证明你的结论.
7.如图,在△ABC中,点Q,M在BC上,点P,N分别在AB,AC上,边BC=120毫米,高AD=80毫米,四边形PQMN为矩形,设△ABC的高AD与PN相交于点E.
(1)若这个矩形是正方形,则边长是多少?
(2)若这个矩形的长是宽的2倍,则长和宽各是多少?
8.如图,用下面的方法可以画△AOB的内接等边三角形,阅读后解答相应问题.
画法:①在△AOB内画等边三角形CDE,使点C在OA上,点D在OB上;②连接OE并延长,交AB于点E′,过点E′作E′C′∥EC,交OA于点C′,作E′D′∥ED,交OB于点D′;③连接C′D′,则△C′D′E′是△AOB的内接等边三角形.
(1)求证:△C′D′E′是等边三角形;
(2)求作:内接于已知△ABC的矩形DEFG,使它的边EF在BC上,顶点D,G分别在AB,AC上,且DE:EF=1:2.
9.如图,A,B两个村子在一条河的同侧,A,B两村到河岸的距离分别为AC=1km,BD=3km,其中CD=3km.现在要在河岸CD上建一个水厂,向A,B两个村庄输送自来水,请你在CD上选择水厂的位置O,使铺设的水管总长度最小?
10.如图,在△ABC中,AC=BC,F为边AB上的一点,BF:AF=m:n(m、n>0),取CF的中点D,连结AD并延长交BC于点E.
(1)求BE:EC的值;
(2)若BE=2EC,那么CF所在的直线与边AB有怎样的位置关系?证明你的结论.
(3)E点能否成为BC中点?若能,求出相应的m:n,若不能,证明你的结论.
参考答案
1.解:(1)△PBM∽△QNM.理由如下:
如图1,∵MQ⊥MP,MN⊥BC(已知),
∴∠PMB+∠PMN=90°,∠QMN+∠PMN=90°,
∴∠PMB=∠QMN(等量代换).
∵∠PBM+∠C=90°(直角三角形的两个锐角互余),∠QNM+∠C=90°(直角三角形的两个锐角互余),
∴∠PBM=∠QNM(等量代换).
∴△PBM∽△QNM;
(2)PQ2=BP2+CQ2.
证明如下:如图1,延长QM至点D,使MD=MQ.连接PD、BD,BQ,CD
∵BC、DQ互相平分,
∴四边形BDCQ为平行四边形,
∴BD∥CQ,BD=CQ(平行四边形的对边平行且相等);
又∵∠BAC=90°,
∴∠PBD=90°,
∴PD2=BP2+BD2=BP2+CQ2,
∵PM垂直平分DQ,
∴PQ=PD,
∴PQ2=BP2+CQ2.
2.解:过点作AM⊥BC于点M,
∵AB=AC=5,BC=6,
∴BM=BC=3,
在Rt△ABM中,AM==4,
∵四边形DEFG是矩形,
∴DG∥EF,DE⊥BC,
∴AN⊥DG,四边形EDMN是矩形,
∴MN=DE,
设MN=DE=x,
∵DG∥EF,
∴△ADG∽△ABC,
∴DG:BC=AN:AM,
∴,
解得:DG=﹣x+6,
∵四边形DEFG为正方形,
∴DE=DG,即x=﹣x+6,
解得x=,
∴正方形DEFG的边长为;
(2)由题意得:DN=2DE,
由(1)知:,
∴DE=.
故答案为:.
3.解:如图,过A作AH垂直ED,垂足为H,交线段FC与G,
由题知,∵FG∥EH,
∴△AFG∽△AEH,
∴=,
又因为AG=BC=2,AH=BD=2+6=8,FG=FC﹣GC=3.2﹣1.6=1.6,
所以=,
解得:EH=6.4,
则ED=EH+HD=6.4+1.6=8(m).
答:树ED的高为8米.
4.证明:(1)∵AB=AC,点M是BC的中点,
∴AM⊥BC,AM平分∠BAC,
∵BN平分∠ABE,
∴∠EBN=∠ABN,
∵AC⊥BD,
∴∠AEB=90°,
∴∠EAB+∠EBA=90°,
∴∠MNB=∠NAB+∠ABN=(∠EAB+∠EBA)=45°,
∴∠MBN=45°;
(2)∵点F,M分别是AB,BC的中点,
∴FM∥AC,FM=AC,
∵AC=BD,
∴FM=BD,即=,
由(1)知△BMN是等腰直角三角形,
∴MN=BM=BC,即=,
∴=,
∵AM⊥BC,
∴∠NMF+∠FMB=90°,
∵FM∥AC,
∴∠ACB=∠FMB,
∵∠CEB=90°,
∴∠ACB+∠CBD=90°,
∴∠CBD+∠FMB=90°,
∴∠NMF=∠CBD,
∴△MFN∽△BDC.
5.解:设正方形EFGH的边长HG=x,
∵EH∥BC,
∴△AEH∽△ABC,
∴=,
解得,x=3,
答:正方形的边长为3.
6.证明:(1)连接AD,过D作DM⊥AB于M,DN⊥EF于N,DK⊥AC于K,
∵AB=AC,
∴AD平分∠BAC,
∴DM=DK,
∵ED平分∠BEF,
∴DM=DN,
∴DM=DN=DK,
∴DF平分∠EFC,
∵∠AEF+∠AFE=180°﹣∠A,
∴∠DEF+∠DFE=[360°﹣(∠AEF+∠AFE)]=180°﹣(180°﹣∠A)=90°+A,
∴∠EDF=90°﹣∠A,
∴∠EDF+∠A=90°;
(2)连接AD,过D作DM⊥AB于M,DN⊥AC于N,过E作EK⊥AD于K,
∵AB=AC,
∴∠ABC=∠ACB=45°,
∴∠BAC=90°,
∵D为BC的中点,
∴∠BAD=∠CAD,
∴DM=DN,
∴四边形AMDN是正方形,AM=AB,
∵AE:BE=1:3,
∴AE=AB,
∴AE=EM,由(1)证得∠EDF+∠A=90°,
∵∠BAC=90°,
∴∠EDF=45°,
∵∠ADN=45°,
∴∠3=∠2,
∵∠APC=∠ADC=90°,
∴A,P,D,C四点共圆,
∴∠1=∠3,∠DPC=∠DAC=45°,
∴DF⊥PC,∴∠1=∠2=∠3,
∴sin∠1=sin∠3,
即=,
设EK=AK=a,则AE=a,AM=2a,AD=4a,
∴KD=3a,ED=a,
∴==.
7.解:(1)设正方形的边长为x毫米,
∵四边形PQMN为正方形,
∴PN∥QM,
∴△APN∽△ABC,
∴,即,
解得x=48,
∴正方形的边长是48mm;
(2)设长方形的宽为y毫米,由(1)得△APN∽△ABC,
∴,即,或,
解得y=30或y=,
∴长方形的宽为30mm,长为60mm或宽为
mm,长为
mm.
8.(1)证明:∵E′C′∥EC,E′D′∥ED,
∴△OCE∽△OC′E′,△ODE∽△OD′E′,
∴CE:C′E′=OE:OE′,DE:D′E′=OE:OE′,∠CEO=∠C′E′O,∠DEO=∠D′E′O,
∴CE:C′E′=DE:D′E′,∠CED=∠C′E′D′,
∴△CDE∽△C′D′E′,
∵△CDE是等边三角形,
∴△C′D′E′是等边三角形;
(2)解:画法:①在△ABC内画矩形D′E′F′G′,使点D′在AB上,点G′在AC上,且D′E′:D′G′=1:2;
②连接AE′并延长,交BC于点E,连接AF′并延长交BC于点F,过点E作ED∥E′D′交AB于点D,过点F作FG∥F′G′,交AC于点G;
③连接DG,则矩形DEFG是△ABC的内接四边形.
9.解:作点A关于CD的对称点E,连结BE交CD于点O,如图,
∵点A关于CD的对称点E,
∴OA=OE,AC=CE=1,
∴OA+OB=OE+OB=BE,
∴此时点O使OA+OB最小,
设OC=xkm,则OD=(3﹣x)km,
∵CE∥BD,
∴△ECO∽△BDO,
∴=,即=,解得x=0.75(km).
答:在CD上选择在离C处0.75km的地方建水厂,使铺设的水管总长度最小.
10.解:(1)如图,过点F作FG∥BC交AE于G,
则∠DFG=∠DCE,∠DGF=∠DEC,
∵D是CF的中点,
∴CD=DF,
在△DCE和△DFG中,
,
∴△DCE≌△DFG(ASA),
∴EC=GF,
∵BF:AF=m:n,
∴=,
∵FG∥BC,
∴△AFG∽△ABE,
∴==,
∴BE:EC=;
(2)若BE=2EC,则BE:EC=2,
由(1)知,=2,
解得m=n,
∴点F是AB的中点,
∵AC=BC,
∴CF⊥AB;
(3)不能.
理由如下:假设点E能成为BC中点,
则BE=EC,
∴BE:EC=1,
由(1)知=1,
解得m=0,
这与m、n>0相矛盾,
所以,点E不能成为BC中点.
