2020-2021学年九年级数学人教版下册第二十七章《相似》综合练习题(word版,含答案)
文档属性
| 名称 | 2020-2021学年九年级数学人教版下册第二十七章《相似》综合练习题(word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 515.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 09:30:20 | ||
图片预览



文档简介
人教版九年级数学下册
第二十七章
相似
综合练习题2
一、选择题
1.如图,在平面直角坐标系xOy中,半径为2的⊙O与x轴的正半轴交于点,点是上一动点,点为弦的中点,直线与x轴、y轴分别交于点,则面积的最小值为( )
A.2
B.2.5
C.
D.
2.如图,AB是的弦(非直径),点C是弦AB上的动点(不与点A,B重合),过点C作垂直于OC的弦DE.设的半径为r,弦AB的长为a,,则弦DE的长( )
A.与r,a,m的值均有关
B.只与r,a的值有关
C.只与r,m的值有关
D.只与a,m的值有关:
3.如图,在平面直角坐标系xOy中,已知△ABO的两个顶点分别为A(﹣8,4),B(﹣2,﹣2),以原点O为位似中心画△,使它与△ABO位似,且相似比为,则点A的对应点的坐标为( )
A.(4,2)
B.(1,1)
C.(﹣4,2)
D.(4,﹣2)
4.点B把线段AC分成两部分,如果=k,那么k的值为(
)
A.
B.
C.+1
D.-1
5.如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平后再次折叠,使点A落在EF上的点A'
处,得到折痕BM,且BM与EF相交于点N,若直线BA'交直线CD于点O,BC
=
,EN
=,则OD的长为(
)
A.
B.1
C.
D.
6.如图,矩形ABCD中,AD=2,
AB=4,
AE平分∠DAC,AE交CD于点F,CE⊥AE,垂足为E,EG⊥CD,垂足为点G,则以下结论:①△EFC∽△ECA;②△ABC≌△AEC;③CE=AF;④;⑤,其中正确的的结论有(
)
A.2个
B.3个
C.4个
D.5个
7.如图,已知A点的坐标为(﹣2,0),⊙B的圆心坐标为(0,﹣1),半径为1,若C是⊙B上的一个动点,射线AC与y轴交于点D(0,b),则b的取值范围是( )
A.
B.b<0
C.﹣2≤b≤0
D.﹣2<b<0
8.如图1,在正方形ABCD中,点F为对角线BD上一点,FE⊥AB于点E,将△EBF绕点B逆时针旋转到图2所示的位置,连接AE、DF,则在图2中,有以下说法:①FD=AE;②∠AEB=
135°;③=1:2;④AE∥BF,其中正确结论的序号是( )
A.①②
B.①③
C.②③
D.③④
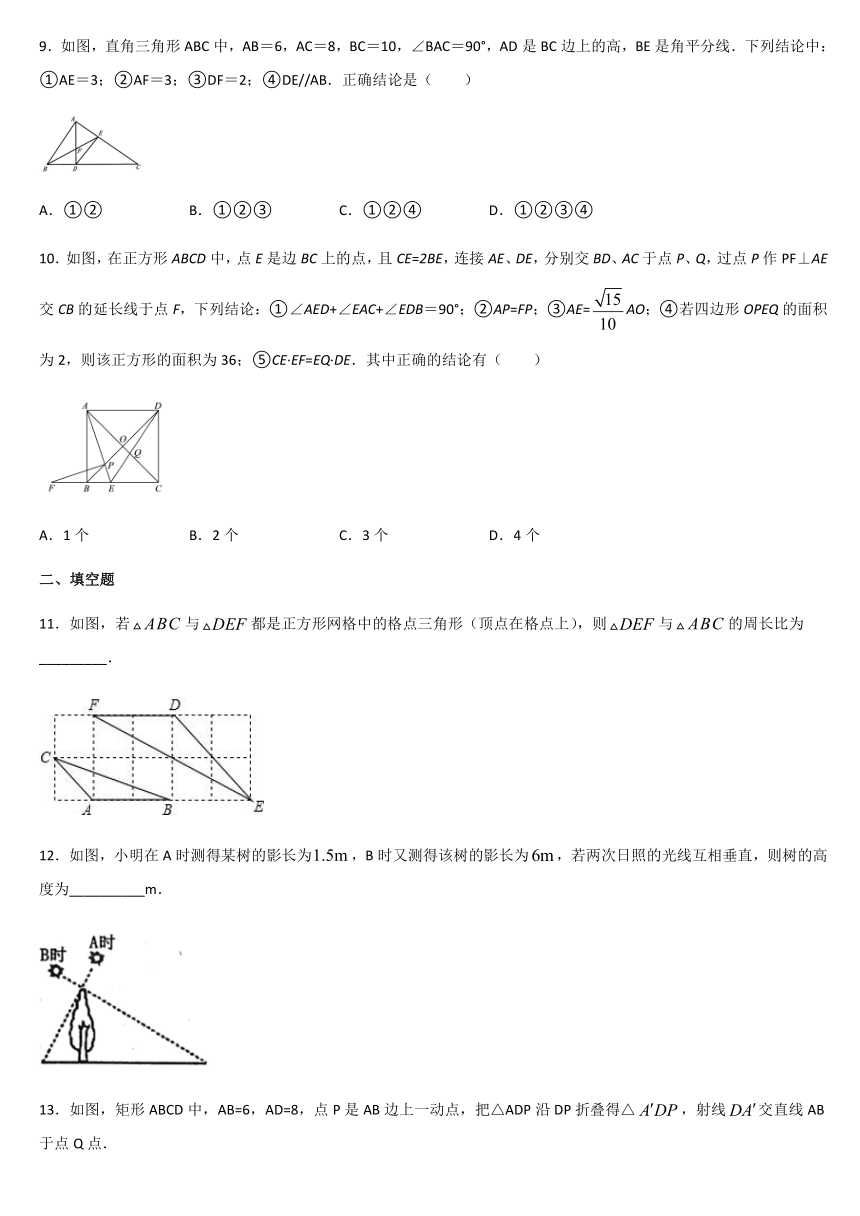
9.如图,直角三角形ABC中,AB=6,AC=8,BC=10,∠BAC=90°,AD是BC边上的高,BE是角平分线.下列结论中:①AE=3;②AF=3;③DF=2;④DE//AB.正确结论是(
)
A.①②
B.①②③
C.①②④
D.①②③④
10.如图,在正方形ABCD中,点E是边BC上的点,且CE=2BE,连接AE、DE,分别交BD、AC于点P、Q,过点P作PF⊥AE交CB的延长线于点F,下列结论:①∠AED+∠EAC+∠EDB=90°;②AP=FP;③AE=AO;④若四边形OPEQ的面积为2,则该正方形的面积为36;⑤CE·EF=EQ·DE.其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
二、填空题
11.如图,若与都是正方形网格中的格点三角形(顶点在格点上),则与的周长比为_________.
12.如图,小明在A时测得某树的影长为,B时又测得该树的影长为,若两次日照的光线互相垂直,则树的高度为__________m.
13.如图,矩形ABCD中,AB=6,AD=8,点P是AB边上一动点,把△ADP沿DP折叠得△,射线交直线AB于点Q点.
(1)当Q点和B点重合时,PQ长为___________;
(2)当△为等腰三角形时,DQ长为____________.
14.如图,在平面直角坐标系xOy中,点A,B在反比例函数y=的图象上(点A在第一象限),且线段AB经过点O,将线段AB绕点A逆时针旋转60°得到线段AC,线段AC交x轴于点D,若,则点C的坐标是_____.
15.如图,在巾,,,,为对角线、的交点,是一条过点且绕点旋转的动直线,过点作于点.则点到直线的距离的最小值为________.
三、解答题
16.如图,已知四边形是矩形,点E在的延长线上,.连与相交于点F,,若,求的值.
17.锐角中,,,两动点M,N分别在边,上滑动,且,以为边向下作正方形,设其边长为x,正方形与公共部分的面积为
(1)中边上高_______;
(2)当恰好落在边上时,求x的值(如图1);
(3)当在外部时(如图2),求y关于x的函数关系式(注明x的取值范围),并求出x为何值时y最大,最大值是多少?
18.已知抛物线y=ax2+bx+3的图象与x轴相交于点A和点B(1,0),与y轴交于点C连接AC,有一动点D在线段AC上运动,过点D作轴的垂线,交抛物线于点E,交轴于点F,AB=4,设点D的横坐标为m.
(1)求抛物线的解析式.
(2)连接AE、CE,当△ACE的面积最大时,求点D的坐标.
(3)当m为何值时,△CDE是等腰三角形.
(4)连接BC,当∠EAD=∠OCB时,请直接写出此时点D的坐标.
19.如果三角形的两个内角与满足=90°,那么我们称这样的三角形为“准互余三角形”.
(1)若△ABC是“准互余三角形”,∠C>90°,∠A=60°,求∠B的度数;
(2)如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5,若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.
20.如图,在平面直角坐标系中,已知矩形的三个顶点,以A为顶点的抛物线过点C.动点P从点A出发,沿线段向点B运动,同时动点Q从点C出发,沿线段向点D运动.点的运动速度均为每秒1个单位,运动时间为t秒.过点P作交于点E.
(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)过点E作于F,交抛物线于点G,当t为何值时,的面积最大?最大值为多少?
(3)在动点运动的过程中,当t为何值时,在矩形ABCD内(包括边界)存在点H,使以C,Q,E,H为顶点的四边形为菱形?请直接写出t的值.
21.如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象相交于点,点A的坐标为,点B的横坐标为6.
(1)求反比例函数与一次函数的解析式;
(2)连结,求的面积;
(3)若点C在x轴上,D点在坐标平面内,是否存在点C,使得以为顶点的四边形是矩形,若存在,求出点D的坐标;求出点的坐标;若不存在,请说明理由.
22.如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)试探究t为何值时,△BPQ是等腰三角形;
(3)试探究t为何值时,CP=CQ;
(4)连接AQ,CP,若AQ⊥CP,求t的值.
23.如图1,两等腰直角三角形和有一条边与在同一直线上,,.设,点在线段上,.
(1)当时,
;
(2)如图2,当时,绕点逆时针旋转,求的值;
(3)如图3,当时,绕点逆时针旋转度,原题中其它条件不变.请直接写出的值(用含的代数式表示)
【参考答案】
1.A
2.D
3.D
4.B
5.B
6.C
7.A
8.B
9.A
10.B
11.
12.3
13.
或
14.()
15.
16..
17.(1)3;(2);(3).;当时,y有最大值,最大值是3.
18.(1);(2);(3)m=-2或-1或;(4).
19.(1)∠B=15°;(2)存在,BE=.
20.(1),;(2)当t=2时,S△ACG的最大值为1;(3)或
21.(1),;(2)8;(3)(,-2)或(,2)或(5,4)或(3,4)
22.(1)1或;(2)或或;(3);(4).
23.(1);(2);(3)
第二十七章
相似
综合练习题2
一、选择题
1.如图,在平面直角坐标系xOy中,半径为2的⊙O与x轴的正半轴交于点,点是上一动点,点为弦的中点,直线与x轴、y轴分别交于点,则面积的最小值为( )
A.2
B.2.5
C.
D.
2.如图,AB是的弦(非直径),点C是弦AB上的动点(不与点A,B重合),过点C作垂直于OC的弦DE.设的半径为r,弦AB的长为a,,则弦DE的长( )
A.与r,a,m的值均有关
B.只与r,a的值有关
C.只与r,m的值有关
D.只与a,m的值有关:
3.如图,在平面直角坐标系xOy中,已知△ABO的两个顶点分别为A(﹣8,4),B(﹣2,﹣2),以原点O为位似中心画△,使它与△ABO位似,且相似比为,则点A的对应点的坐标为( )
A.(4,2)
B.(1,1)
C.(﹣4,2)
D.(4,﹣2)
4.点B把线段AC分成两部分,如果=k,那么k的值为(
)
A.
B.
C.+1
D.-1
5.如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平后再次折叠,使点A落在EF上的点A'
处,得到折痕BM,且BM与EF相交于点N,若直线BA'交直线CD于点O,BC
=
,EN
=,则OD的长为(
)
A.
B.1
C.
D.
6.如图,矩形ABCD中,AD=2,
AB=4,
AE平分∠DAC,AE交CD于点F,CE⊥AE,垂足为E,EG⊥CD,垂足为点G,则以下结论:①△EFC∽△ECA;②△ABC≌△AEC;③CE=AF;④;⑤,其中正确的的结论有(
)
A.2个
B.3个
C.4个
D.5个
7.如图,已知A点的坐标为(﹣2,0),⊙B的圆心坐标为(0,﹣1),半径为1,若C是⊙B上的一个动点,射线AC与y轴交于点D(0,b),则b的取值范围是( )
A.
B.b<0
C.﹣2≤b≤0
D.﹣2<b<0
8.如图1,在正方形ABCD中,点F为对角线BD上一点,FE⊥AB于点E,将△EBF绕点B逆时针旋转到图2所示的位置,连接AE、DF,则在图2中,有以下说法:①FD=AE;②∠AEB=
135°;③=1:2;④AE∥BF,其中正确结论的序号是( )
A.①②
B.①③
C.②③
D.③④
9.如图,直角三角形ABC中,AB=6,AC=8,BC=10,∠BAC=90°,AD是BC边上的高,BE是角平分线.下列结论中:①AE=3;②AF=3;③DF=2;④DE//AB.正确结论是(
)
A.①②
B.①②③
C.①②④
D.①②③④
10.如图,在正方形ABCD中,点E是边BC上的点,且CE=2BE,连接AE、DE,分别交BD、AC于点P、Q,过点P作PF⊥AE交CB的延长线于点F,下列结论:①∠AED+∠EAC+∠EDB=90°;②AP=FP;③AE=AO;④若四边形OPEQ的面积为2,则该正方形的面积为36;⑤CE·EF=EQ·DE.其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
二、填空题
11.如图,若与都是正方形网格中的格点三角形(顶点在格点上),则与的周长比为_________.
12.如图,小明在A时测得某树的影长为,B时又测得该树的影长为,若两次日照的光线互相垂直,则树的高度为__________m.
13.如图,矩形ABCD中,AB=6,AD=8,点P是AB边上一动点,把△ADP沿DP折叠得△,射线交直线AB于点Q点.
(1)当Q点和B点重合时,PQ长为___________;
(2)当△为等腰三角形时,DQ长为____________.
14.如图,在平面直角坐标系xOy中,点A,B在反比例函数y=的图象上(点A在第一象限),且线段AB经过点O,将线段AB绕点A逆时针旋转60°得到线段AC,线段AC交x轴于点D,若,则点C的坐标是_____.
15.如图,在巾,,,,为对角线、的交点,是一条过点且绕点旋转的动直线,过点作于点.则点到直线的距离的最小值为________.
三、解答题
16.如图,已知四边形是矩形,点E在的延长线上,.连与相交于点F,,若,求的值.
17.锐角中,,,两动点M,N分别在边,上滑动,且,以为边向下作正方形,设其边长为x,正方形与公共部分的面积为
(1)中边上高_______;
(2)当恰好落在边上时,求x的值(如图1);
(3)当在外部时(如图2),求y关于x的函数关系式(注明x的取值范围),并求出x为何值时y最大,最大值是多少?
18.已知抛物线y=ax2+bx+3的图象与x轴相交于点A和点B(1,0),与y轴交于点C连接AC,有一动点D在线段AC上运动,过点D作轴的垂线,交抛物线于点E,交轴于点F,AB=4,设点D的横坐标为m.
(1)求抛物线的解析式.
(2)连接AE、CE,当△ACE的面积最大时,求点D的坐标.
(3)当m为何值时,△CDE是等腰三角形.
(4)连接BC,当∠EAD=∠OCB时,请直接写出此时点D的坐标.
19.如果三角形的两个内角与满足=90°,那么我们称这样的三角形为“准互余三角形”.
(1)若△ABC是“准互余三角形”,∠C>90°,∠A=60°,求∠B的度数;
(2)如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5,若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.
20.如图,在平面直角坐标系中,已知矩形的三个顶点,以A为顶点的抛物线过点C.动点P从点A出发,沿线段向点B运动,同时动点Q从点C出发,沿线段向点D运动.点的运动速度均为每秒1个单位,运动时间为t秒.过点P作交于点E.
(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)过点E作于F,交抛物线于点G,当t为何值时,的面积最大?最大值为多少?
(3)在动点运动的过程中,当t为何值时,在矩形ABCD内(包括边界)存在点H,使以C,Q,E,H为顶点的四边形为菱形?请直接写出t的值.
21.如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象相交于点,点A的坐标为,点B的横坐标为6.
(1)求反比例函数与一次函数的解析式;
(2)连结,求的面积;
(3)若点C在x轴上,D点在坐标平面内,是否存在点C,使得以为顶点的四边形是矩形,若存在,求出点D的坐标;求出点的坐标;若不存在,请说明理由.
22.如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)试探究t为何值时,△BPQ是等腰三角形;
(3)试探究t为何值时,CP=CQ;
(4)连接AQ,CP,若AQ⊥CP,求t的值.
23.如图1,两等腰直角三角形和有一条边与在同一直线上,,.设,点在线段上,.
(1)当时,
;
(2)如图2,当时,绕点逆时针旋转,求的值;
(3)如图3,当时,绕点逆时针旋转度,原题中其它条件不变.请直接写出的值(用含的代数式表示)
【参考答案】
1.A
2.D
3.D
4.B
5.B
6.C
7.A
8.B
9.A
10.B
11.
12.3
13.
或
14.()
15.
16..
17.(1)3;(2);(3).;当时,y有最大值,最大值是3.
18.(1);(2);(3)m=-2或-1或;(4).
19.(1)∠B=15°;(2)存在,BE=.
20.(1),;(2)当t=2时,S△ACG的最大值为1;(3)或
21.(1),;(2)8;(3)(,-2)或(,2)或(5,4)或(3,4)
22.(1)1或;(2)或或;(3);(4).
23.(1);(2);(3)
