湘教版八年级数学下册 1.3直角三角形全等的判定(Word版 含答案)
文档属性
| 名称 | 湘教版八年级数学下册 1.3直角三角形全等的判定(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 189.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 10:59:19 | ||
图片预览


文档简介
1.3直角三角形全等的判定
1.如图,∠B=∠E=90°,AB=DE,AC=DF,则△ABC≌△DEF的理由是( )
A.SAS B.ASA
C.AAS D.HL
2.如图,OD⊥AB于点D,OP⊥AC于点P,且OD=OP,则△AOD与△AOP全等的理由是( )
A.SSS B.ASA C.SSA D.HL
3.如图,在△ABC中,∠C=90°,ED⊥AB于点D,BD=BC,若AC=6 cm,则AE+DE等于( )
A.4 cm B.5 cm C.6 cm D.7 cm
4.如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加的一个条件是( )
A.AE=DF B.∠A=∠D
C.∠B=∠C D.AB=DC
【点拨】添加条件AB=DC.
理由:∵AE⊥BC,DF⊥BC,∴∠AEB=∠CFD=90°.
在Rt△ABE和Rt△DCF中,
∴Rt△ABE≌Rt△DCF(HL),故选D.
5.下列条件中,不能判定两个直角三角形全等的是( )
A.两条直角边对应相等
B.两个锐角对应相等
C.一个锐角和一条直角边对应相等
D.斜边和一条直角边对应相等
6.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC
C.∠BCA=∠DCA D.∠B=∠D=90°
7.如图,CD⊥AB,BE⊥AC,垂足分别为点D,E,BE与CD相交于点O,且∠1=∠2,则下列结论正确的个数为( )
①∠B=∠C;
②△ADO≌△AEO;
③△BOD≌△COE;
④图中有4对三角形全等.
A.1个 B.2个 C.3个 D.4个
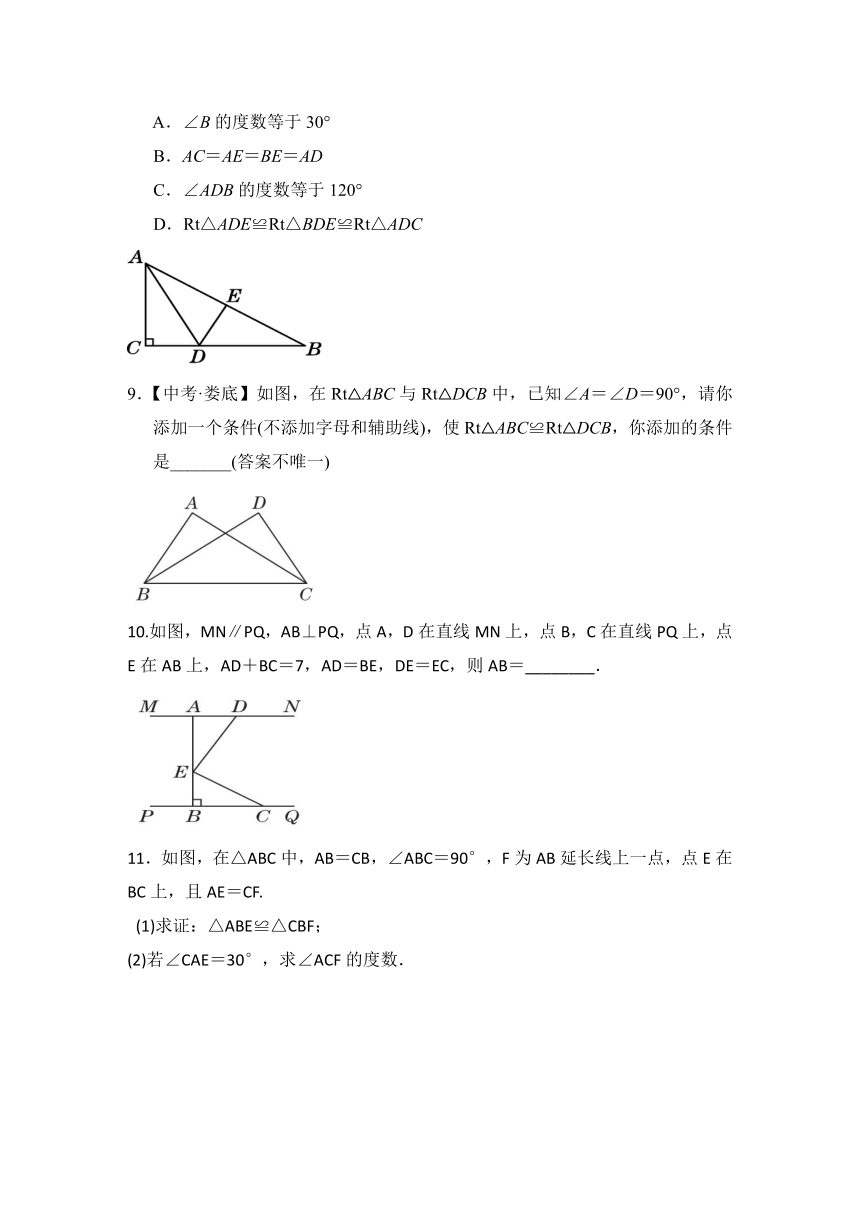
8.如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线交BC于点D,交AB于点E,AD平分∠BAC,则下列结论不正确的是( )
A.∠B的度数等于30°
B.AC=AE=BE=AD
C.∠ADB的度数等于120°
D.Rt△ADE≌Rt△BDE≌Rt△ADC
9.【中考·娄底】如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,请你添加一个条件(不添加字母和辅助线),使Rt△ABC≌Rt△DCB,你添加的条件是_______(答案不唯一)
10.如图,MN∥PQ,AB⊥PQ,点A,D在直线MN上,点B,C在直线PQ上,点E在AB上,AD+BC=7,AD=BE,DE=EC,则AB=________.
11.如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
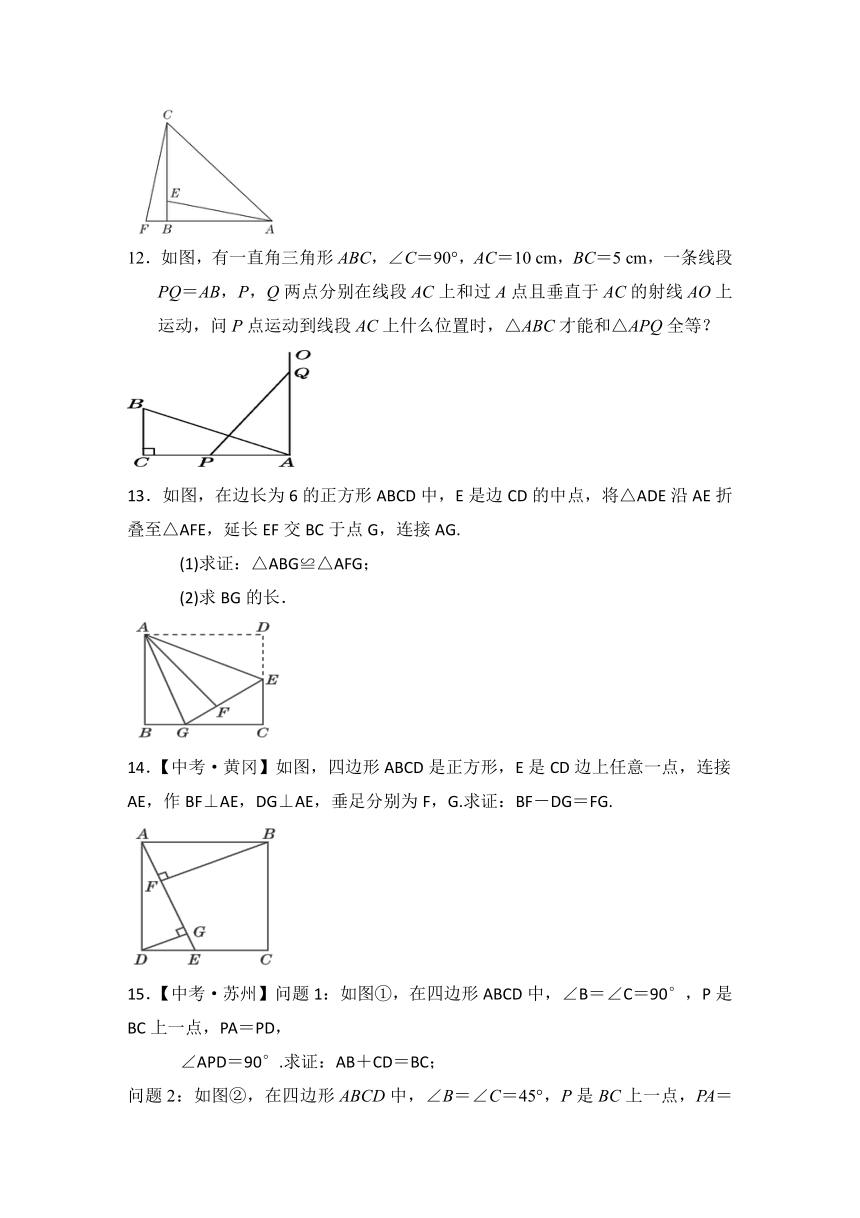
12.如图,有一直角三角形ABC,∠C=90°,AC=10 cm,BC=5 cm,一条线段PQ=AB,P,Q两点分别在线段AC上和过A点且垂直于AC的射线AO上运动,问P点运动到线段AC上什么位置时,△ABC才能和△APQ全等?
13.如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE折叠至△AFE,延长EF交BC于点G,连接AG.
(1)求证:△ABG≌△AFG;
(2)求BG的长.
14.【中考·黄冈】如图,四边形ABCD是正方形,E是CD边上任意一点,连接AE,作BF⊥AE,DG⊥AE,垂足分别为F,G.求证:BF-DG=FG.
15.【中考·苏州】问题1:如图①,在四边形ABCD中,∠B=∠C=90°,P是BC上一点,PA=PD,
∠APD=90°.求证:AB+CD=BC;
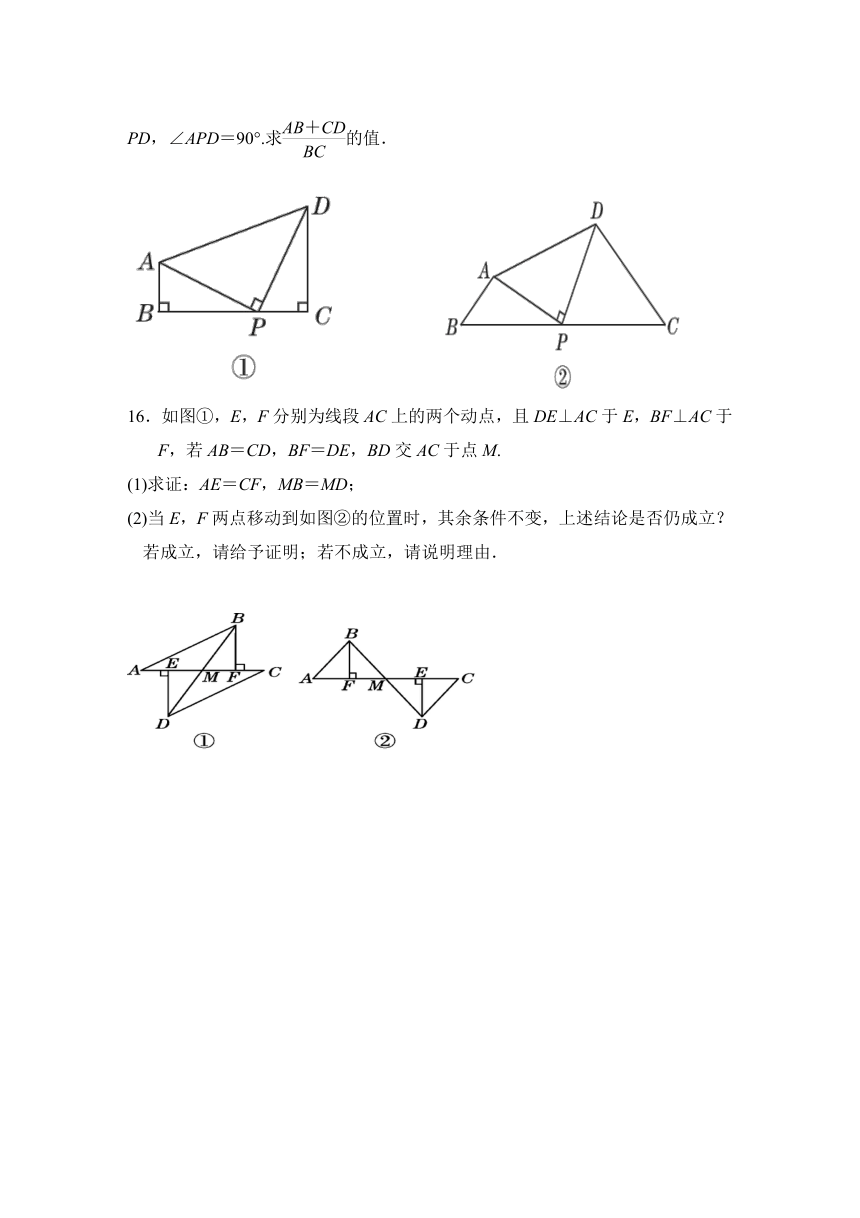
问题2:如图②,在四边形ABCD中,∠B=∠C=45°,P是BC上一点,PA=PD,∠APD=90°.求的值.
16.如图①,E,F分别为线段AC上的两个动点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,BF=DE,BD交AC于点M.
(1)求证:AE=CF,MB=MD;
(2)当E,F两点移动到如图②的位置时,其余条件不变,上述结论是否仍成立?若成立,请给予证明;若不成立,请说明理由.
1.3直角三角形全等的判定
1.如图,∠B=∠E=90°,AB=DE,AC=DF,则△ABC≌△DEF的理由是( D )
A.SAS B.ASA
C.AAS D.HL
2.如图,OD⊥AB于点D,OP⊥AC于点P,且OD=OP,则△AOD与△AOP全等的理由是(D )
A.SSS B.ASA C.SSA D.HL
3.如图,在△ABC中,∠C=90°,ED⊥AB于点D,BD=BC,若AC=6 cm,则AE+DE等于( C )
A.4 cm B.5 cm C.6 cm D.7 cm
4.如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加的一个条件是( D )
A.AE=DF B.∠A=∠D
C.∠B=∠C D.AB=DC
【点拨】添加条件AB=DC.
理由:∵AE⊥BC,DF⊥BC,∴∠AEB=∠CFD=90°.
在Rt△ABE和Rt△DCF中,
∴Rt△ABE≌Rt△DCF(HL),故选D.
5.下列条件中,不能判定两个直角三角形全等的是( B )
A.两条直角边对应相等
B.两个锐角对应相等
C.一个锐角和一条直角边对应相等
D.斜边和一条直角边对应相等
6.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( C )
A.CB=CD B.∠BAC=∠DAC
C.∠BCA=∠DCA D.∠B=∠D=90°
7.如图,CD⊥AB,BE⊥AC,垂足分别为点D,E,BE与CD相交于点O,且∠1=∠2,则下列结论正确的个数为( D )
①∠B=∠C;
②△ADO≌△AEO;
③△BOD≌△COE;
④图中有4对三角形全等.
A.1个 B.2个 C.3个 D.4个
8.如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线交BC于点D,交AB于点E,AD平分∠BAC,则下列结论不正确的是( B )
A.∠B的度数等于30°
B.AC=AE=BE=AD
C.∠ADB的度数等于120°
D.Rt△ADE≌Rt△BDE≌Rt△ADC
9.【中考·娄底】如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,请你添加一个条件(不添加字母和辅助线),使Rt△ABC≌Rt△DCB,你添加的条件是___AB=CD____(答案不唯一)
10.如图,MN∥PQ,AB⊥PQ,点A,D在直线MN上,点B,C在直线PQ上,点E在AB上,AD+BC=7,AD=BE,DE=EC,则AB=__7______.
【点拨】易证△ADE≌△BEC,得AE=BC.
又AD=BE,故AB=AE+BE=BC+AD=7.
11.如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
证明:(1)∵∠ABC=90°,
∴∠CBF=∠ABE=90°.
在Rt△ABE和Rt△CBF中,
∴Rt△ABE≌Rt△CBF(HL).
(2)∵AB=BC,∠ABC=90°,
∴∠CAB=∠ACB=45°.
∴∠BAE=∠CAB-∠CAE=45°-30°=15°.
由(1)知Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=15°,
∴∠ACF=∠BCF+∠ACB=15°+45°=60°.
12.如图,有一直角三角形ABC,∠C=90°,AC=10 cm,BC=5 cm,一条线段PQ=AB,P,Q两点分别在线段AC上和过A点且垂直于AC的射线AO上运动,问P点运动到线段AC上什么位置时,△ABC才能和△APQ全等?
解:①当AP=BC时,易知AP=CP=5 cm,∠C=∠QAP=90°.
在Rt△ABC与Rt△QPA中,
∵AB=PQ,BC=AP,∴Rt△ABC≌Rt△QPA(HL).
②当P点与C点重合时,AP=AC.
在Rt△QAP与Rt△BCA中,
∵PQ=AB,AP=CA,∴Rt△QAP≌Rt△BCA(HL).
综上,当P点运动到线段AC的中点或与C点重合时△ABC才能和△APQ全等.
13.如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE折叠至△AFE,延长EF交BC于点G,连接AG.
(1)求证:△ABG≌△AFG;
(2)求BG的长.
证明:(1)在正方形ABCD中,AD=AB,∠D=∠B=90°.
∵将△ADE沿AE折叠至△AFE,
∴AD=AF,DE=EF,∠D=∠AFE=90°.
∴AB=AF,∠B=∠AFG=90°.
在Rt△ABG与Rt△AFG中,
∴Rt△ABG≌Rt△AFG(HL).
(2):由(1)知Rt△ABG≌Rt△AFG,∴BG=FG.
设BG=FG=x(x>0),则GC=6-x,
∵E为CD的中点,∴CE=DE=EF=3,∴EG=3+x.
在Rt△CEG中,CE2+GC2=EG2,
即32+(6-x)2=(3+x)2,解得x=2.∴BG=2.
14.【中考·黄冈】如图,四边形ABCD是正方形,E是CD边上任意一点,连接AE,作BF⊥AE,DG⊥AE,垂足分别为F,G.求证:BF-DG=FG.
证明:∵四边形ABCD为正方形,
∴∠DAB=90°,AD=AB.
∵BF⊥AE,DG⊥AE,∴∠AFB=∠DGA=90°.
∴∠DAG+∠FAB=∠DAG+∠ADG=90°,
∴∠FAB=∠GDA.∴△ABF≌△DAG(AAS).
∴BF=AG,AF=DG.
∴BF-DG=AG-AF=FG.
15.【中考·苏州】问题1:如图①,在四边形ABCD中,∠B=∠C=90°,P是BC上一点,PA=PD,
∠APD=90°.求证:AB+CD=BC;
问题2:如图②,在四边形ABCD中,∠B=∠C=45°,P是BC上一点,PA=PD,∠APD=90°.求的值.
证明:(1)∵∠B=90°,∠APD=90°,∴∠BAP+∠APB=90°,
∠APB+∠CPD=90°,∴∠BAP=∠CPD.
又PA=DP,∠B=∠C=90°,∴△BAP≌△CPD(AAS),∴BP=CD,AB=PC,∴BC=PC+BP=AB+CD,即AB+CD=BC.
(2):如图,过点A作AE⊥BC于点E,过点D作DF⊥BC于点F,由问题1可知,EF=AE+DF,∵∠B=∠C=45°,AE⊥BC,DF⊥BC,∴∠BAE=45°=∠B,∠CDF=45°=∠C,∴BE=AE,CF=DF,∴BC=BE+EF+CF=2(AE+DF),在Rt△ABE中,AB2=BE2+AE2=2AE2,
∴AB=AE,同理CD=DF,
∴==.
16.如图①,E,F分别为线段AC上的两个动点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,BF=DE,BD交AC于点M.
(1)求证:AE=CF,MB=MD;
(2)当E,F两点移动到如图②的位置时,其余条件不变,上述结论是否仍成立?若成立,请给予证明;若不成立,请说明理由.
证明:(1)∵DE⊥AC,BF⊥AC,∴∠CED=∠BFA=90°.
在Rt△ABF和Rt△CDE中,
∴Rt△ABF≌Rt△CDE(HL),
∴AF=CE,∴AF-EF=CE-EF,即AE=CF.
在△DEM和△BFM中,
∴△DEM≌△BFM(AAS),∴MB=MD.
解:AE=CF,MB=MD仍成立.
证明如下:在Rt△ABF和Rt△CDE中,
∴Rt△ABF≌Rt△CDE(HL),∴AF=CE,
∴AF+EF=CE+EF,即AE=CF.
在△DEM和△BFM中,
∴△DEM≌△BFM(AAS),∴MB=MD.
1.如图,∠B=∠E=90°,AB=DE,AC=DF,则△ABC≌△DEF的理由是( )
A.SAS B.ASA
C.AAS D.HL
2.如图,OD⊥AB于点D,OP⊥AC于点P,且OD=OP,则△AOD与△AOP全等的理由是( )
A.SSS B.ASA C.SSA D.HL
3.如图,在△ABC中,∠C=90°,ED⊥AB于点D,BD=BC,若AC=6 cm,则AE+DE等于( )
A.4 cm B.5 cm C.6 cm D.7 cm
4.如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加的一个条件是( )
A.AE=DF B.∠A=∠D
C.∠B=∠C D.AB=DC
【点拨】添加条件AB=DC.
理由:∵AE⊥BC,DF⊥BC,∴∠AEB=∠CFD=90°.
在Rt△ABE和Rt△DCF中,
∴Rt△ABE≌Rt△DCF(HL),故选D.
5.下列条件中,不能判定两个直角三角形全等的是( )
A.两条直角边对应相等
B.两个锐角对应相等
C.一个锐角和一条直角边对应相等
D.斜边和一条直角边对应相等
6.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC
C.∠BCA=∠DCA D.∠B=∠D=90°
7.如图,CD⊥AB,BE⊥AC,垂足分别为点D,E,BE与CD相交于点O,且∠1=∠2,则下列结论正确的个数为( )
①∠B=∠C;
②△ADO≌△AEO;
③△BOD≌△COE;
④图中有4对三角形全等.
A.1个 B.2个 C.3个 D.4个
8.如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线交BC于点D,交AB于点E,AD平分∠BAC,则下列结论不正确的是( )
A.∠B的度数等于30°
B.AC=AE=BE=AD
C.∠ADB的度数等于120°
D.Rt△ADE≌Rt△BDE≌Rt△ADC
9.【中考·娄底】如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,请你添加一个条件(不添加字母和辅助线),使Rt△ABC≌Rt△DCB,你添加的条件是_______(答案不唯一)
10.如图,MN∥PQ,AB⊥PQ,点A,D在直线MN上,点B,C在直线PQ上,点E在AB上,AD+BC=7,AD=BE,DE=EC,则AB=________.
11.如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
12.如图,有一直角三角形ABC,∠C=90°,AC=10 cm,BC=5 cm,一条线段PQ=AB,P,Q两点分别在线段AC上和过A点且垂直于AC的射线AO上运动,问P点运动到线段AC上什么位置时,△ABC才能和△APQ全等?
13.如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE折叠至△AFE,延长EF交BC于点G,连接AG.
(1)求证:△ABG≌△AFG;
(2)求BG的长.
14.【中考·黄冈】如图,四边形ABCD是正方形,E是CD边上任意一点,连接AE,作BF⊥AE,DG⊥AE,垂足分别为F,G.求证:BF-DG=FG.
15.【中考·苏州】问题1:如图①,在四边形ABCD中,∠B=∠C=90°,P是BC上一点,PA=PD,
∠APD=90°.求证:AB+CD=BC;
问题2:如图②,在四边形ABCD中,∠B=∠C=45°,P是BC上一点,PA=PD,∠APD=90°.求的值.
16.如图①,E,F分别为线段AC上的两个动点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,BF=DE,BD交AC于点M.
(1)求证:AE=CF,MB=MD;
(2)当E,F两点移动到如图②的位置时,其余条件不变,上述结论是否仍成立?若成立,请给予证明;若不成立,请说明理由.
1.3直角三角形全等的判定
1.如图,∠B=∠E=90°,AB=DE,AC=DF,则△ABC≌△DEF的理由是( D )
A.SAS B.ASA
C.AAS D.HL
2.如图,OD⊥AB于点D,OP⊥AC于点P,且OD=OP,则△AOD与△AOP全等的理由是(D )
A.SSS B.ASA C.SSA D.HL
3.如图,在△ABC中,∠C=90°,ED⊥AB于点D,BD=BC,若AC=6 cm,则AE+DE等于( C )
A.4 cm B.5 cm C.6 cm D.7 cm
4.如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加的一个条件是( D )
A.AE=DF B.∠A=∠D
C.∠B=∠C D.AB=DC
【点拨】添加条件AB=DC.
理由:∵AE⊥BC,DF⊥BC,∴∠AEB=∠CFD=90°.
在Rt△ABE和Rt△DCF中,
∴Rt△ABE≌Rt△DCF(HL),故选D.
5.下列条件中,不能判定两个直角三角形全等的是( B )
A.两条直角边对应相等
B.两个锐角对应相等
C.一个锐角和一条直角边对应相等
D.斜边和一条直角边对应相等
6.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( C )
A.CB=CD B.∠BAC=∠DAC
C.∠BCA=∠DCA D.∠B=∠D=90°
7.如图,CD⊥AB,BE⊥AC,垂足分别为点D,E,BE与CD相交于点O,且∠1=∠2,则下列结论正确的个数为( D )
①∠B=∠C;
②△ADO≌△AEO;
③△BOD≌△COE;
④图中有4对三角形全等.
A.1个 B.2个 C.3个 D.4个
8.如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线交BC于点D,交AB于点E,AD平分∠BAC,则下列结论不正确的是( B )
A.∠B的度数等于30°
B.AC=AE=BE=AD
C.∠ADB的度数等于120°
D.Rt△ADE≌Rt△BDE≌Rt△ADC
9.【中考·娄底】如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,请你添加一个条件(不添加字母和辅助线),使Rt△ABC≌Rt△DCB,你添加的条件是___AB=CD____(答案不唯一)
10.如图,MN∥PQ,AB⊥PQ,点A,D在直线MN上,点B,C在直线PQ上,点E在AB上,AD+BC=7,AD=BE,DE=EC,则AB=__7______.
【点拨】易证△ADE≌△BEC,得AE=BC.
又AD=BE,故AB=AE+BE=BC+AD=7.
11.如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
证明:(1)∵∠ABC=90°,
∴∠CBF=∠ABE=90°.
在Rt△ABE和Rt△CBF中,
∴Rt△ABE≌Rt△CBF(HL).
(2)∵AB=BC,∠ABC=90°,
∴∠CAB=∠ACB=45°.
∴∠BAE=∠CAB-∠CAE=45°-30°=15°.
由(1)知Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=15°,
∴∠ACF=∠BCF+∠ACB=15°+45°=60°.
12.如图,有一直角三角形ABC,∠C=90°,AC=10 cm,BC=5 cm,一条线段PQ=AB,P,Q两点分别在线段AC上和过A点且垂直于AC的射线AO上运动,问P点运动到线段AC上什么位置时,△ABC才能和△APQ全等?
解:①当AP=BC时,易知AP=CP=5 cm,∠C=∠QAP=90°.
在Rt△ABC与Rt△QPA中,
∵AB=PQ,BC=AP,∴Rt△ABC≌Rt△QPA(HL).
②当P点与C点重合时,AP=AC.
在Rt△QAP与Rt△BCA中,
∵PQ=AB,AP=CA,∴Rt△QAP≌Rt△BCA(HL).
综上,当P点运动到线段AC的中点或与C点重合时△ABC才能和△APQ全等.
13.如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE折叠至△AFE,延长EF交BC于点G,连接AG.
(1)求证:△ABG≌△AFG;
(2)求BG的长.
证明:(1)在正方形ABCD中,AD=AB,∠D=∠B=90°.
∵将△ADE沿AE折叠至△AFE,
∴AD=AF,DE=EF,∠D=∠AFE=90°.
∴AB=AF,∠B=∠AFG=90°.
在Rt△ABG与Rt△AFG中,
∴Rt△ABG≌Rt△AFG(HL).
(2):由(1)知Rt△ABG≌Rt△AFG,∴BG=FG.
设BG=FG=x(x>0),则GC=6-x,
∵E为CD的中点,∴CE=DE=EF=3,∴EG=3+x.
在Rt△CEG中,CE2+GC2=EG2,
即32+(6-x)2=(3+x)2,解得x=2.∴BG=2.
14.【中考·黄冈】如图,四边形ABCD是正方形,E是CD边上任意一点,连接AE,作BF⊥AE,DG⊥AE,垂足分别为F,G.求证:BF-DG=FG.
证明:∵四边形ABCD为正方形,
∴∠DAB=90°,AD=AB.
∵BF⊥AE,DG⊥AE,∴∠AFB=∠DGA=90°.
∴∠DAG+∠FAB=∠DAG+∠ADG=90°,
∴∠FAB=∠GDA.∴△ABF≌△DAG(AAS).
∴BF=AG,AF=DG.
∴BF-DG=AG-AF=FG.
15.【中考·苏州】问题1:如图①,在四边形ABCD中,∠B=∠C=90°,P是BC上一点,PA=PD,
∠APD=90°.求证:AB+CD=BC;
问题2:如图②,在四边形ABCD中,∠B=∠C=45°,P是BC上一点,PA=PD,∠APD=90°.求的值.
证明:(1)∵∠B=90°,∠APD=90°,∴∠BAP+∠APB=90°,
∠APB+∠CPD=90°,∴∠BAP=∠CPD.
又PA=DP,∠B=∠C=90°,∴△BAP≌△CPD(AAS),∴BP=CD,AB=PC,∴BC=PC+BP=AB+CD,即AB+CD=BC.
(2):如图,过点A作AE⊥BC于点E,过点D作DF⊥BC于点F,由问题1可知,EF=AE+DF,∵∠B=∠C=45°,AE⊥BC,DF⊥BC,∴∠BAE=45°=∠B,∠CDF=45°=∠C,∴BE=AE,CF=DF,∴BC=BE+EF+CF=2(AE+DF),在Rt△ABE中,AB2=BE2+AE2=2AE2,
∴AB=AE,同理CD=DF,
∴==.
16.如图①,E,F分别为线段AC上的两个动点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,BF=DE,BD交AC于点M.
(1)求证:AE=CF,MB=MD;
(2)当E,F两点移动到如图②的位置时,其余条件不变,上述结论是否仍成立?若成立,请给予证明;若不成立,请说明理由.
证明:(1)∵DE⊥AC,BF⊥AC,∴∠CED=∠BFA=90°.
在Rt△ABF和Rt△CDE中,
∴Rt△ABF≌Rt△CDE(HL),
∴AF=CE,∴AF-EF=CE-EF,即AE=CF.
在△DEM和△BFM中,
∴△DEM≌△BFM(AAS),∴MB=MD.
解:AE=CF,MB=MD仍成立.
证明如下:在Rt△ABF和Rt△CDE中,
∴Rt△ABF≌Rt△CDE(HL),∴AF=CE,
∴AF+EF=CE+EF,即AE=CF.
在△DEM和△BFM中,
∴△DEM≌△BFM(AAS),∴MB=MD.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
