湘教版八年级数学下册 1.4.1 角平分线的性质与判定(Word版 含答案)
文档属性
| 名称 | 湘教版八年级数学下册 1.4.1 角平分线的性质与判定(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 240.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 11:00:18 | ||
图片预览



文档简介
1.4.1 角平分线的性质与判定
1.如图,已知BG是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,DE=6,则DF的长度是( )
A.2 B.3
C.4 D.6
2.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B,连接AB.下列结论中不一定成立的是( )
A.PA=PB
B.PO平分∠APB
C.OA=OB
D.AB垂直平分OP
3.如图,已知BD是∠ABC的平分线,ED是BC的垂直平分线,∠BAC=90°,AD=3,则CE的长为( D )
A.6 B.5
C.4 D.3
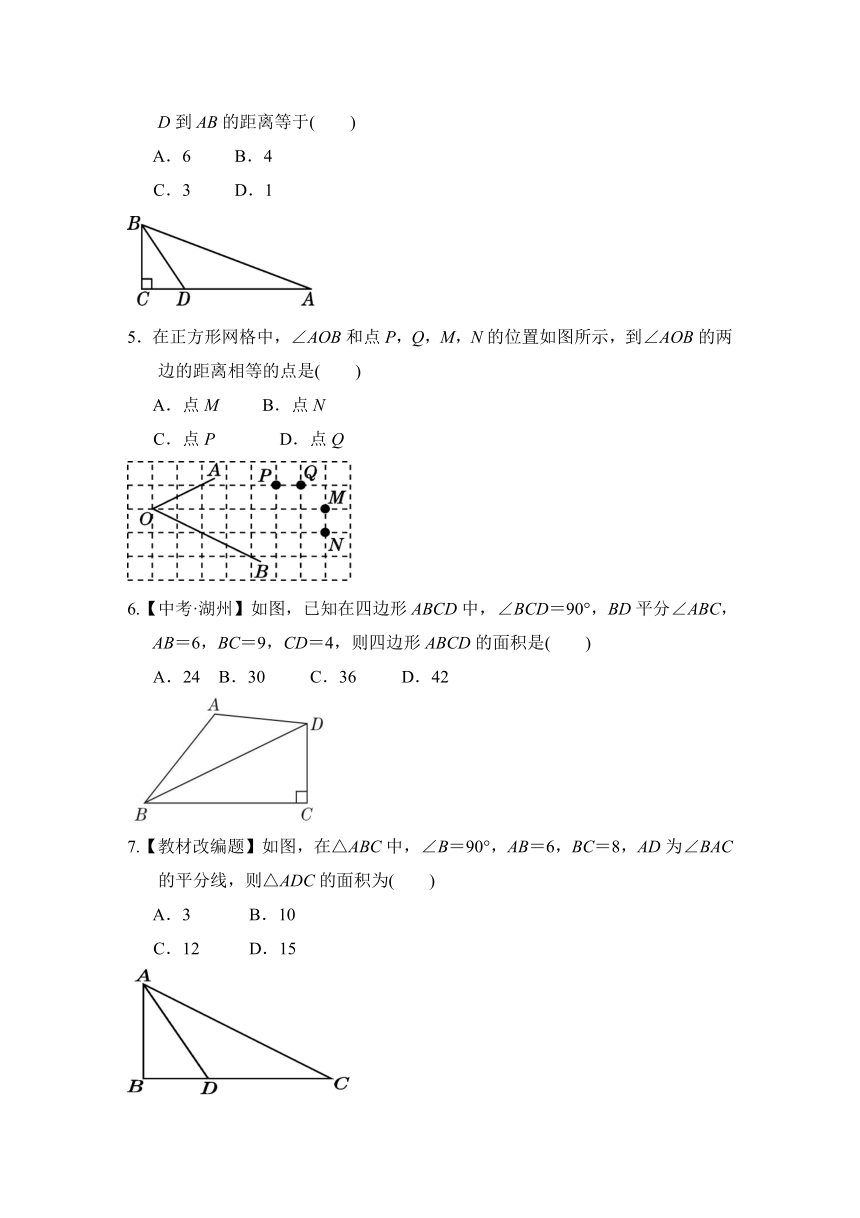
4.如图,在△ABC中,∠C=90°,AC=12,DC=AD,BD平分∠ABC,则点D到AB的距离等于( )
A.6 B.4
C.3 D.1
5.在正方形网格中,∠AOB和点P,Q,M,N的位置如图所示,到∠AOB的两边的距离相等的点是( )
A.点M B.点N
C.点P D.点Q
6.【中考·湖州】如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是( )
A.24 B.30 C.36 D.42
7.【教材改编题】如图,在△ABC中,∠B=90°,AB=6,BC=8,AD为∠BAC的平分线,则△ADC的面积为( )
A.3 B.10
C.12 D.15
8.如图,AB=AC,BE⊥AC于E,CF⊥AB于F,BE与CF相交于D,则①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.正确的结论是( )
A.①②③ B.②③
C.①③ D.①
9.【中考·永州】如图,已知∠AOB=60°,OC是∠AOB的平分线,点D为OC上一点,过D作直线DE⊥OA,垂足为点E,且直线DE交OB于点F.若DE=2,则DF=________.
10.如图,已知BD⊥AE于点B,DC⊥AF于点C,且DB=DC,∠BAC=40°,∠ADG=130°,则∠DGF=_______.
11.【中考·湘潭】如图,点P是∠AOC的平分线上一点,PD⊥OA,垂足为点D,且PD=3,点M是射线OC上一动点,则PM的最小值为________.
12.【中考·福建】如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,求作∠ABC的平分线,分别交AD,AC于P,Q两点,并证明AP=AQ.(要求:尺规作图,保留作图痕迹,不写作法)
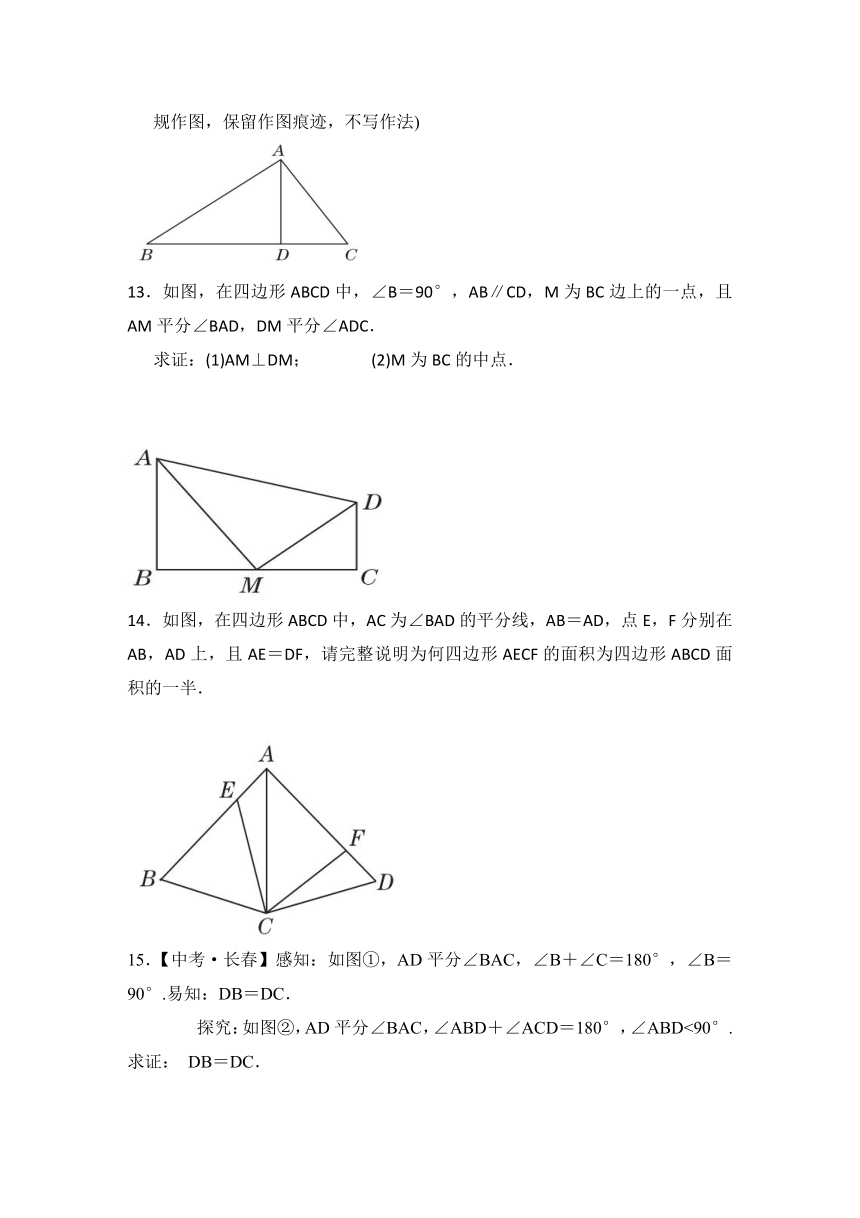
如图,在四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.
求证:(1)AM⊥DM; (2)M为BC的中点.
14.如图,在四边形ABCD中,AC为∠BAD的平分线,AB=AD,点E,F分别在AB,AD上,且AE=DF,请完整说明为何四边形AECF的面积为四边形ABCD面积的一半.
15.【中考·长春】感知:如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°.易知:DB=DC.
探究:如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°.求证: DB=DC.
已知∠MAN=120°,AC平分∠MAN,点B,D分别在AN,AM上.
(1)如图①,若∠ABC=∠ADC=90°,请你探索线段AD,AB,AC之间的数量关系,并证明;
(2)如图②,若∠ABC+∠ADC=180°,则(1)中的结论是否仍成立?若成立,请给出证明;若不成立,请说明理由.
1.4.1 角平分线的性质与判定
1.如图,已知BG是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,DE=6,则DF的长度是( D )
A.2 B.3
C.4 D.6
【点拨】∵BG是∠ABC的平分线,DE⊥AB,DF⊥BC,∴DF=DE=6.
2.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B,连接AB.下列结论中不一定成立的是( D )
A.PA=PB
B.PO平分∠APB
C.OA=OB
D.AB垂直平分OP
3.如图,已知BD是∠ABC的平分线,ED是BC的垂直平分线,∠BAC=90°,AD=3,则CE的长为( D )
A.6 B.5
C.4 D.3
【点拨】∵ED是BC的垂直平分线,
∴DB=DC,∴∠C=∠DBC.
∵BD是∠ABC的平分线,DE⊥BC,AB⊥AC,
∴∠ABD=∠DBC,DE=AD=3.
又∵∠BAC=90°,∴∠C=∠DBC=∠ABD=30°,
∴CD=2DE=6,∴CE==3 .
4.如图,在△ABC中,∠C=90°,AC=12,DC=AD,BD平分∠ABC,则点D到AB的距离等于( C )
A.6 B.4
C.3 D.1
【点拨】如图,过点D作DE⊥AB于E,
∵AC=12,DC=AD,
∴CD=12×=3.
∵CD⊥BC,ED⊥BE,BD平分∠ABC,
∴DE=CD=3,即点D到AB的距离为3.
5.在正方形网格中,∠AOB和点P,Q,M,N的位置如图所示,到∠AOB的两边的距离相等的点是( A )
A.点M B.点N
C.点P D.点Q
6.【中考·湖州】如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是( B )
A.24 B.30 C.36 D.42
【点拨】如图,过D作DH⊥AB交BA的延长线于H.
∵BD平分∠ABC,∠BCD=90°,∴DH=CD=4,
∴四边形ABCD的面积=S△ABD+S△BCD=AB·DH+BC·CD=×6×4+×9×4=30.
7.【教材改编题】如图,在△ABC中,∠B=90°,AB=6,BC=8,AD为∠BAC的平分线,则△ADC的面积为( D )
A.3 B.10
C.12 D.15
【点拨】过点D作DH⊥AC于H,如图.
∵在△ABC中,∠B=90°,AB=6,BC=8,
∴AC==10.
∵AD为∠BAC的平分线,AB⊥BD,DH⊥AC,∴DB=DH,
∵S△ADC=AB·CD=DH·AC,
∴6(8-DH)=10DH,解得DH=3,∴S△ADC=×10×3=15.
8.如图,AB=AC,BE⊥AC于E,CF⊥AB于F,BE与CF相交于D,则①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.正确的结论是( A )
A.①②③ B.②③
C.①③ D.①
9.【中考·永州】如图,已知∠AOB=60°,OC是∠AOB的平分线,点D为OC上一点,过D作直线DE⊥OA,垂足为点E,且直线DE交OB于点F.若DE=2,则DF=___4_____.
【点拨】过D作DN⊥OB于点N.
∵∠AOB=60°,OC是∠AOB的平分线,DE⊥OA,DN⊥OB,∴∠AOC=∠COB=30°,DN=DE=2.
∵DE⊥OA,∴∠DFO=90°-60°=30°,∴DF=2DN=4.
10.如图,已知BD⊥AE于点B,DC⊥AF于点C,且DB=DC,∠BAC=40°,∠ADG=130°,则∠DGF=__150°._____.
【点拨】∵BD⊥AE于点B,DC⊥AF于点C,且DB=DC,
∴AD是∠BAC的平分线.
∵∠BAC=40°,∴∠CAD=∠BAC=20°,
∴∠DGF=∠CAD+∠ADG=20°+130°=150°.
11.【中考·湘潭】如图,点P是∠AOC的平分线上一点,PD⊥OA,垂足为点D,且PD=3,点M是射线OC上一动点,则PM的最小值为___3_____.
12.【中考·福建】如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,求作∠ABC的平分线,分别交AD,AC于P,Q两点,并证明AP=AQ.(要求:尺规作图,保留作图痕迹,不写作法)
解:如图,BQ就是∠ABC的平分线.
证明如下:过点A作AM⊥PQ于点M,则∠AMP=∠AMQ=90°.∵AD⊥BC,∴∠ADB=90°.∴∠BPD+∠PBD=90°.∵∠BAC=90°,
∴∠AQM+∠ABQ=90°.∵∠ABQ=∠PBD,∴∠BPD=∠AQM.
∵∠BPD=∠APM,∴∠APM=∠AQM.在△APM和△AQM中,∴△APM≌△AQM(AAS).∴AP=AQ.
如图,在四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.
求证:(1)AM⊥DM; (2)M为BC的中点.
证明:(1)∵AB∥CD,
∴∠BAD+∠ADC=180°.
∵AM平分∠BAD,DM平分∠ADC,
∴2∠MAD+2∠ADM=180°.
∴∠MAD+∠ADM=90°.
∴∠AMD=90°,即AM⊥DM.
(2):如图,过M作MN⊥AD交AD于点N,
∵∠B=90°,AB∥CD,∴BM⊥AB,CM⊥CD.
又∵AM平分∠BAD,DM平分∠ADC,
∴BM=MN,MN=CM,
∴BM=CM,即M为BC的中点.
14.如图,在四边形ABCD中,AC为∠BAD的平分线,AB=AD,点E,F分别在AB,AD上,且AE=DF,请完整说明为何四边形AECF的面积为四边形ABCD面积的一半.
【点拨】本题利用角平分线的性质,
证S△ABC=S△ACD,S△AEC=S△CDF,从而得到结论.
解:如图,过点C作CG⊥AB于点G,CH⊥AD于点H.
∵AC为∠BAD的平分线,∴CG=CH.∵AB=AD,
∴S△ABC=S△ACD=S四边形ABCD.又∵AE=DF,∴S△AEC=S△CDF.
∴S四边形AECF=S△AEC+S△ACF=S△CDF+S△ACF=S△ACD=S四边形ABCD,
即四边形AECF的面积为四边形ABCD面积的一半.
15.【中考·长春】感知:如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°.易知:DB=DC.
探究:如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°.求证: DB=DC.
【点拨】本题根据∠ACD与∠FCD是邻补角及
∠ABD+∠ACD=180°得出∠B=∠FCD,再根据全等三角形的判定与性质得出结论.
证明:如图,过点D分别作DE⊥AB于点E,DF⊥AC交AC的延长线于点F.∵AD平分∠BAC,DE⊥AB,DF⊥AC,∴DE=DF.∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD.
在△DFC和△DEB中,
∴△DFC≌△DEB(AAS).∴DB=DC.
已知∠MAN=120°,AC平分∠MAN,点B,D分别在AN,AM上.
(1)如图①,若∠ABC=∠ADC=90°,请你探索线段AD,AB,AC之间的数量关系,并证明;
(2)如图②,若∠ABC+∠ADC=180°,则(1)中的结论是否仍成立?若成立,请给出证明;若不成立,请说明理由.
解:关系是AD+AB=AC.
证明:∵AC平分∠MAN,∠MAN=120°,
∴∠CAD=∠CAB=60°.
又∠ADC=∠ABC=90°,
∴∠ACD=∠ACB=30°.
∴AD=AB=AC. ∴AD+AB=AC.
(2):仍成立.
证明:如图,过点C作CE⊥AM于E,
CF⊥AN于F.
∵AC平分∠MAN,CE⊥AM,CF⊥AN,
∴CE=CF.
∵∠ABC+∠ADC=180°,∠ADC+∠CDE=180°,
∴∠CDE=∠ABC.
又∵∠CED=∠CFB=90°,
∴△CED≌△CFB.
∴ED=FB,∴AD+AB=AE-ED+AF+FB=AE+AF.
由(1)易知AE+AF=AC. ∴AD+AB=AC.
1.如图,已知BG是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,DE=6,则DF的长度是( )
A.2 B.3
C.4 D.6
2.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B,连接AB.下列结论中不一定成立的是( )
A.PA=PB
B.PO平分∠APB
C.OA=OB
D.AB垂直平分OP
3.如图,已知BD是∠ABC的平分线,ED是BC的垂直平分线,∠BAC=90°,AD=3,则CE的长为( D )
A.6 B.5
C.4 D.3
4.如图,在△ABC中,∠C=90°,AC=12,DC=AD,BD平分∠ABC,则点D到AB的距离等于( )
A.6 B.4
C.3 D.1
5.在正方形网格中,∠AOB和点P,Q,M,N的位置如图所示,到∠AOB的两边的距离相等的点是( )
A.点M B.点N
C.点P D.点Q
6.【中考·湖州】如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是( )
A.24 B.30 C.36 D.42
7.【教材改编题】如图,在△ABC中,∠B=90°,AB=6,BC=8,AD为∠BAC的平分线,则△ADC的面积为( )
A.3 B.10
C.12 D.15
8.如图,AB=AC,BE⊥AC于E,CF⊥AB于F,BE与CF相交于D,则①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.正确的结论是( )
A.①②③ B.②③
C.①③ D.①
9.【中考·永州】如图,已知∠AOB=60°,OC是∠AOB的平分线,点D为OC上一点,过D作直线DE⊥OA,垂足为点E,且直线DE交OB于点F.若DE=2,则DF=________.
10.如图,已知BD⊥AE于点B,DC⊥AF于点C,且DB=DC,∠BAC=40°,∠ADG=130°,则∠DGF=_______.
11.【中考·湘潭】如图,点P是∠AOC的平分线上一点,PD⊥OA,垂足为点D,且PD=3,点M是射线OC上一动点,则PM的最小值为________.
12.【中考·福建】如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,求作∠ABC的平分线,分别交AD,AC于P,Q两点,并证明AP=AQ.(要求:尺规作图,保留作图痕迹,不写作法)
如图,在四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.
求证:(1)AM⊥DM; (2)M为BC的中点.
14.如图,在四边形ABCD中,AC为∠BAD的平分线,AB=AD,点E,F分别在AB,AD上,且AE=DF,请完整说明为何四边形AECF的面积为四边形ABCD面积的一半.
15.【中考·长春】感知:如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°.易知:DB=DC.
探究:如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°.求证: DB=DC.
已知∠MAN=120°,AC平分∠MAN,点B,D分别在AN,AM上.
(1)如图①,若∠ABC=∠ADC=90°,请你探索线段AD,AB,AC之间的数量关系,并证明;
(2)如图②,若∠ABC+∠ADC=180°,则(1)中的结论是否仍成立?若成立,请给出证明;若不成立,请说明理由.
1.4.1 角平分线的性质与判定
1.如图,已知BG是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,DE=6,则DF的长度是( D )
A.2 B.3
C.4 D.6
【点拨】∵BG是∠ABC的平分线,DE⊥AB,DF⊥BC,∴DF=DE=6.
2.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B,连接AB.下列结论中不一定成立的是( D )
A.PA=PB
B.PO平分∠APB
C.OA=OB
D.AB垂直平分OP
3.如图,已知BD是∠ABC的平分线,ED是BC的垂直平分线,∠BAC=90°,AD=3,则CE的长为( D )
A.6 B.5
C.4 D.3
【点拨】∵ED是BC的垂直平分线,
∴DB=DC,∴∠C=∠DBC.
∵BD是∠ABC的平分线,DE⊥BC,AB⊥AC,
∴∠ABD=∠DBC,DE=AD=3.
又∵∠BAC=90°,∴∠C=∠DBC=∠ABD=30°,
∴CD=2DE=6,∴CE==3 .
4.如图,在△ABC中,∠C=90°,AC=12,DC=AD,BD平分∠ABC,则点D到AB的距离等于( C )
A.6 B.4
C.3 D.1
【点拨】如图,过点D作DE⊥AB于E,
∵AC=12,DC=AD,
∴CD=12×=3.
∵CD⊥BC,ED⊥BE,BD平分∠ABC,
∴DE=CD=3,即点D到AB的距离为3.
5.在正方形网格中,∠AOB和点P,Q,M,N的位置如图所示,到∠AOB的两边的距离相等的点是( A )
A.点M B.点N
C.点P D.点Q
6.【中考·湖州】如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是( B )
A.24 B.30 C.36 D.42
【点拨】如图,过D作DH⊥AB交BA的延长线于H.
∵BD平分∠ABC,∠BCD=90°,∴DH=CD=4,
∴四边形ABCD的面积=S△ABD+S△BCD=AB·DH+BC·CD=×6×4+×9×4=30.
7.【教材改编题】如图,在△ABC中,∠B=90°,AB=6,BC=8,AD为∠BAC的平分线,则△ADC的面积为( D )
A.3 B.10
C.12 D.15
【点拨】过点D作DH⊥AC于H,如图.
∵在△ABC中,∠B=90°,AB=6,BC=8,
∴AC==10.
∵AD为∠BAC的平分线,AB⊥BD,DH⊥AC,∴DB=DH,
∵S△ADC=AB·CD=DH·AC,
∴6(8-DH)=10DH,解得DH=3,∴S△ADC=×10×3=15.
8.如图,AB=AC,BE⊥AC于E,CF⊥AB于F,BE与CF相交于D,则①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.正确的结论是( A )
A.①②③ B.②③
C.①③ D.①
9.【中考·永州】如图,已知∠AOB=60°,OC是∠AOB的平分线,点D为OC上一点,过D作直线DE⊥OA,垂足为点E,且直线DE交OB于点F.若DE=2,则DF=___4_____.
【点拨】过D作DN⊥OB于点N.
∵∠AOB=60°,OC是∠AOB的平分线,DE⊥OA,DN⊥OB,∴∠AOC=∠COB=30°,DN=DE=2.
∵DE⊥OA,∴∠DFO=90°-60°=30°,∴DF=2DN=4.
10.如图,已知BD⊥AE于点B,DC⊥AF于点C,且DB=DC,∠BAC=40°,∠ADG=130°,则∠DGF=__150°._____.
【点拨】∵BD⊥AE于点B,DC⊥AF于点C,且DB=DC,
∴AD是∠BAC的平分线.
∵∠BAC=40°,∴∠CAD=∠BAC=20°,
∴∠DGF=∠CAD+∠ADG=20°+130°=150°.
11.【中考·湘潭】如图,点P是∠AOC的平分线上一点,PD⊥OA,垂足为点D,且PD=3,点M是射线OC上一动点,则PM的最小值为___3_____.
12.【中考·福建】如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,求作∠ABC的平分线,分别交AD,AC于P,Q两点,并证明AP=AQ.(要求:尺规作图,保留作图痕迹,不写作法)
解:如图,BQ就是∠ABC的平分线.
证明如下:过点A作AM⊥PQ于点M,则∠AMP=∠AMQ=90°.∵AD⊥BC,∴∠ADB=90°.∴∠BPD+∠PBD=90°.∵∠BAC=90°,
∴∠AQM+∠ABQ=90°.∵∠ABQ=∠PBD,∴∠BPD=∠AQM.
∵∠BPD=∠APM,∴∠APM=∠AQM.在△APM和△AQM中,∴△APM≌△AQM(AAS).∴AP=AQ.
如图,在四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.
求证:(1)AM⊥DM; (2)M为BC的中点.
证明:(1)∵AB∥CD,
∴∠BAD+∠ADC=180°.
∵AM平分∠BAD,DM平分∠ADC,
∴2∠MAD+2∠ADM=180°.
∴∠MAD+∠ADM=90°.
∴∠AMD=90°,即AM⊥DM.
(2):如图,过M作MN⊥AD交AD于点N,
∵∠B=90°,AB∥CD,∴BM⊥AB,CM⊥CD.
又∵AM平分∠BAD,DM平分∠ADC,
∴BM=MN,MN=CM,
∴BM=CM,即M为BC的中点.
14.如图,在四边形ABCD中,AC为∠BAD的平分线,AB=AD,点E,F分别在AB,AD上,且AE=DF,请完整说明为何四边形AECF的面积为四边形ABCD面积的一半.
【点拨】本题利用角平分线的性质,
证S△ABC=S△ACD,S△AEC=S△CDF,从而得到结论.
解:如图,过点C作CG⊥AB于点G,CH⊥AD于点H.
∵AC为∠BAD的平分线,∴CG=CH.∵AB=AD,
∴S△ABC=S△ACD=S四边形ABCD.又∵AE=DF,∴S△AEC=S△CDF.
∴S四边形AECF=S△AEC+S△ACF=S△CDF+S△ACF=S△ACD=S四边形ABCD,
即四边形AECF的面积为四边形ABCD面积的一半.
15.【中考·长春】感知:如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°.易知:DB=DC.
探究:如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°.求证: DB=DC.
【点拨】本题根据∠ACD与∠FCD是邻补角及
∠ABD+∠ACD=180°得出∠B=∠FCD,再根据全等三角形的判定与性质得出结论.
证明:如图,过点D分别作DE⊥AB于点E,DF⊥AC交AC的延长线于点F.∵AD平分∠BAC,DE⊥AB,DF⊥AC,∴DE=DF.∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD.
在△DFC和△DEB中,
∴△DFC≌△DEB(AAS).∴DB=DC.
已知∠MAN=120°,AC平分∠MAN,点B,D分别在AN,AM上.
(1)如图①,若∠ABC=∠ADC=90°,请你探索线段AD,AB,AC之间的数量关系,并证明;
(2)如图②,若∠ABC+∠ADC=180°,则(1)中的结论是否仍成立?若成立,请给出证明;若不成立,请说明理由.
解:关系是AD+AB=AC.
证明:∵AC平分∠MAN,∠MAN=120°,
∴∠CAD=∠CAB=60°.
又∠ADC=∠ABC=90°,
∴∠ACD=∠ACB=30°.
∴AD=AB=AC. ∴AD+AB=AC.
(2):仍成立.
证明:如图,过点C作CE⊥AM于E,
CF⊥AN于F.
∵AC平分∠MAN,CE⊥AM,CF⊥AN,
∴CE=CF.
∵∠ABC+∠ADC=180°,∠ADC+∠CDE=180°,
∴∠CDE=∠ABC.
又∵∠CED=∠CFB=90°,
∴△CED≌△CFB.
∴ED=FB,∴AD+AB=AE-ED+AF+FB=AE+AF.
由(1)易知AE+AF=AC. ∴AD+AB=AC.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
