2020-2021学年八年级下学期数学北师大版 1.2.1直角三角形(第一课时)课件(20张)
文档属性
| 名称 | 2020-2021学年八年级下学期数学北师大版 1.2.1直角三角形(第一课时)课件(20张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 11:03:39 | ||
图片预览






文档简介
北师大版八年级(下)
1.2直角三角形
第一章 三角形的证明
第1回 直角三角形的性质及判定
学习目标
1.能证明直角三角形的性质定理和判定定理.
2.了解逆命题的概念和互逆命题的知识.
3.进一步掌握推理证明的方法,提高演绎推理能力.
知识回顾!
①直角三角形的两个锐角互余.
1 什么是直角三角形?
有一个角是直角的三角形叫直角三角形.
2 我们已经探究出了直角三角形的哪些性质?
②在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
③在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°.
忆直角,性质判定忒多,颇为烧脑!
④勾股定理
探索新知!
想一想
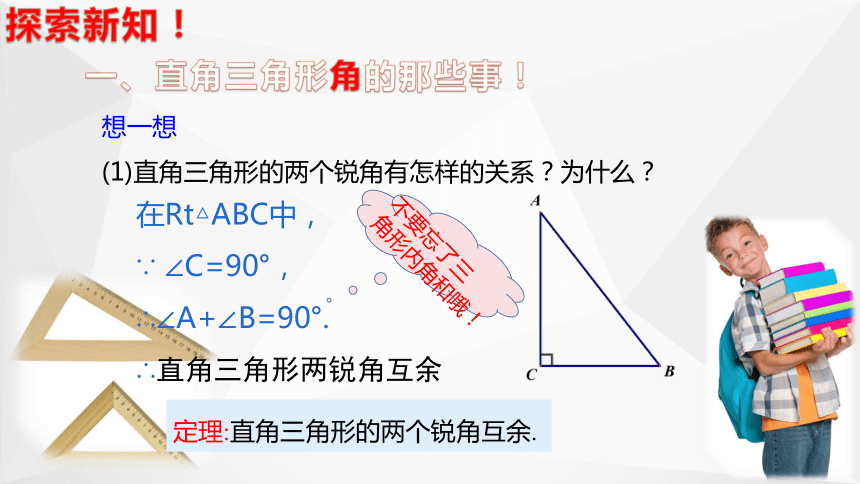
(1) 直角三角形的两个锐角有怎样的关系?为什么?
如果一个三角形有两个角互余,那么这个三角形
是直角三角形吗?为 什么?
一、直角三角形角的那些事!
如何证明呢?
探索新知!
想一想
(1) 直角三角形的两个锐角有怎样的关系?为什么?
一、直角三角形角的那些事!
在Rt△ABC中,
∵ ∠C=90°,
∴∠A+∠B=90°.
∴直角三角形两锐角互余
不要忘了三
角形内角和哦!
定理:直角三角形的两个锐角互余.
探索新知!
想一想
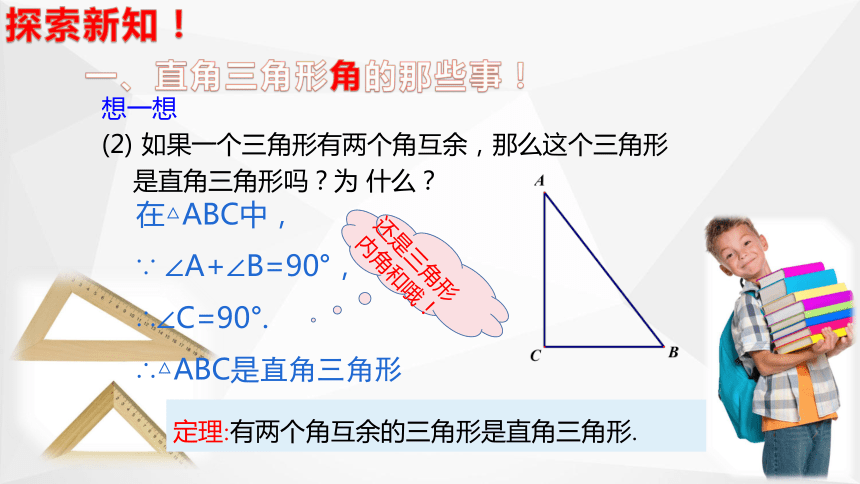
如果一个三角形有两个角互余,那么这个三角形
是直角三角形吗?为 什么?
一、直角三角形角的那些事!
在△ABC中,
∵ ∠A+∠B=90°,
∴∠C=90°.
∴△ABC是直角三角形
还是三角形
内角和哦!
定理:有两个角互余的三角形是直角三角形.
探索新知!
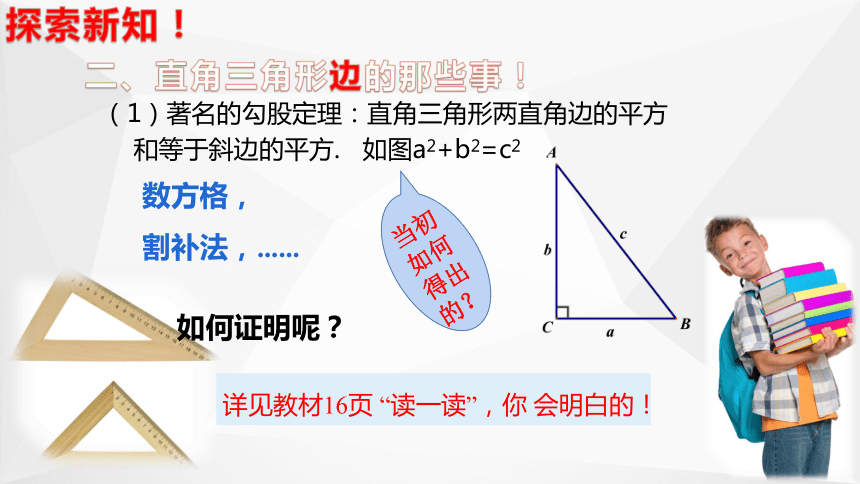
(1)著名的勾股定理:直角三角形两直角边的平方和等于斜边的平方. 如图a2+b2=c2
二、直角三角形边的那些事!
数方格,
割补法,......
详见教材16页 “读一读”,你 会明白的!
当初如何得出的?
如何证明呢?
如果一个三角形两边的平方和等于第三边的平方,
那么这个三角形是直角三角形.
想一想:把勾股定理的条件和结论互换,会得到怎样一个命题呢?
这个命题是真命题吗?为什么?
探索新知!
二、直角三角形边的那些事!
有点烧脑哦!
看老师表演吧!
已知:如图,在△ABC 中, AB2+AC2=BC2.
求证: △ABC是直角三角形 .
证明:如图(2),作Rt △A′B′C′ ,使∠A′=90° A′B′=AB, A′C′=AC,
则A′B′ 2+A′C′ 2 =B′C′ 2(勾股定理).
∵AB2+AC2=BC2 ,
∴BC2 = B′C′ 2.
∴BC = B′C′.
∴△ABC≌ △A′B′C′ (SSS).
∴ ∠A=∠A′=90°(全等三角形的对应角相等).
∴△ABC是直角三角形.
探索新知!
探索新知!
(1)著名的勾股定理:直角三角形两直角边的平方和等于斜边的平方. 如图a2+b2=c2
二、直角三角形边的那些事!
(2)直角三角形判定定理:如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
a2+b2=c2
a2+b2=c2
+
知识小结!
(1)直角三角形两个锐角互余
(2)勾股定理:直角三角形两直角边的平方和等于斜边的平方. 如图a2+b2=c2
直角三角形的性质
(1)有两个角互余的三角形是直角三角形
(2)如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
直角三角形的判定
议一议:观察下面三组命题,它们的条件和结论之间有怎样的关系?
如果两个角是对顶角,那么它们相等;
如果两个角相等,那么它们是对顶角.
如果小明患了新冠肺炎,那么他一定会发烧;
如果小明发烧,那么他一定患了新冠肺炎.
条件和结论互换了位置
新知再探!
两直线平行,内错角相等;
内错角相等,两直线平行.
在两个命题中,如果第一个命题的条件和结论,分别是另一个命题的结论和条件,那么这两个命题叫做互逆命题.
新知再探!
在两个命题中,如果第一个命题的条件和结论,分别是另一个命题的结论和条件,那么这两个命题叫做互逆命题.
一个命题是真命题,它的逆命题不一定是真命题哦!
原命题:如果两个角是对顶角,那么它们相等;
逆命题:如果两个角相等,那么它们是对顶角.
真
假
议一议:观察下面两组定理,它们是互逆命题吗?
定理:直角三角形的两个锐角互余.
定理:有两个角互余的三角形是直角三角形.
定理:直角三角形两条直角边的平方和等于斜边的平方.
定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
新知再探!
如果一个定理的逆命题也是定理,那么这两个定理叫做互逆定理,其中的一个定理叫做另一个定理的逆定理.
实战演练!
1.在△ABC中,已知∠A=∠B=45°,BC =3,求AB的长.
2.已知:在△ABC中,AB=13㎝,BC =10㎝,BC边上的中线AD=12㎝.求证:AB=AC.
3.说出下列命题的逆命题,并判断每对命题的真假:
(1) 四边形是多边形;
(2)两直线平行,同旁内角互补;
(3)如果ab=0,那么a=0,b=0.
请同学们先独立思考完成,然后进行交流展示!
提高练习!
2.如图,在直角△ABC中,D为斜边AB的中点,DE⊥DF,而E、F分别在AC和BC上,连接EF,请问AE、EF、BF能否组成直角三角形,给出你的结论并说明理由.
中点
垂直
倍长“类中线”
提高练习!
2.如图,在直角△ABC中,D为斜边AB的中点,DE⊥DF,而E、F分别在AC和BC上,连接EF,请问AE、EF、BF能否组成直角三角形,给出你的结论并说明理由.
剩下的证明过程,相信你能搞定哦!
直角三角形
角的性质
边的性质
勾股定理:直角三角形两条直角边的平方和等于斜边的平方;
逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
定理1:直角三角形的两个锐角互余;
定理2:有两个角互余的三角形是直角三角形
既是互逆命题又是互逆定理
我的收获!
1.教材习题1.5
2.对应练习册
课后练习
宝宝不哭,作业不会太多哦!
1.2直角三角形
第一章 三角形的证明
第1回 直角三角形的性质及判定
学习目标
1.能证明直角三角形的性质定理和判定定理.
2.了解逆命题的概念和互逆命题的知识.
3.进一步掌握推理证明的方法,提高演绎推理能力.
知识回顾!
①直角三角形的两个锐角互余.
1 什么是直角三角形?
有一个角是直角的三角形叫直角三角形.
2 我们已经探究出了直角三角形的哪些性质?
②在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
③在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°.
忆直角,性质判定忒多,颇为烧脑!
④勾股定理
探索新知!
想一想
(1) 直角三角形的两个锐角有怎样的关系?为什么?
如果一个三角形有两个角互余,那么这个三角形
是直角三角形吗?为 什么?
一、直角三角形角的那些事!
如何证明呢?
探索新知!
想一想
(1) 直角三角形的两个锐角有怎样的关系?为什么?
一、直角三角形角的那些事!
在Rt△ABC中,
∵ ∠C=90°,
∴∠A+∠B=90°.
∴直角三角形两锐角互余
不要忘了三
角形内角和哦!
定理:直角三角形的两个锐角互余.
探索新知!
想一想
如果一个三角形有两个角互余,那么这个三角形
是直角三角形吗?为 什么?
一、直角三角形角的那些事!
在△ABC中,
∵ ∠A+∠B=90°,
∴∠C=90°.
∴△ABC是直角三角形
还是三角形
内角和哦!
定理:有两个角互余的三角形是直角三角形.
探索新知!
(1)著名的勾股定理:直角三角形两直角边的平方和等于斜边的平方. 如图a2+b2=c2
二、直角三角形边的那些事!
数方格,
割补法,......
详见教材16页 “读一读”,你 会明白的!
当初如何得出的?
如何证明呢?
如果一个三角形两边的平方和等于第三边的平方,
那么这个三角形是直角三角形.
想一想:把勾股定理的条件和结论互换,会得到怎样一个命题呢?
这个命题是真命题吗?为什么?
探索新知!
二、直角三角形边的那些事!
有点烧脑哦!
看老师表演吧!
已知:如图,在△ABC 中, AB2+AC2=BC2.
求证: △ABC是直角三角形 .
证明:如图(2),作Rt △A′B′C′ ,使∠A′=90° A′B′=AB, A′C′=AC,
则A′B′ 2+A′C′ 2 =B′C′ 2(勾股定理).
∵AB2+AC2=BC2 ,
∴BC2 = B′C′ 2.
∴BC = B′C′.
∴△ABC≌ △A′B′C′ (SSS).
∴ ∠A=∠A′=90°(全等三角形的对应角相等).
∴△ABC是直角三角形.
探索新知!
探索新知!
(1)著名的勾股定理:直角三角形两直角边的平方和等于斜边的平方. 如图a2+b2=c2
二、直角三角形边的那些事!
(2)直角三角形判定定理:如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
a2+b2=c2
a2+b2=c2
+
知识小结!
(1)直角三角形两个锐角互余
(2)勾股定理:直角三角形两直角边的平方和等于斜边的平方. 如图a2+b2=c2
直角三角形的性质
(1)有两个角互余的三角形是直角三角形
(2)如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
直角三角形的判定
议一议:观察下面三组命题,它们的条件和结论之间有怎样的关系?
如果两个角是对顶角,那么它们相等;
如果两个角相等,那么它们是对顶角.
如果小明患了新冠肺炎,那么他一定会发烧;
如果小明发烧,那么他一定患了新冠肺炎.
条件和结论互换了位置
新知再探!
两直线平行,内错角相等;
内错角相等,两直线平行.
在两个命题中,如果第一个命题的条件和结论,分别是另一个命题的结论和条件,那么这两个命题叫做互逆命题.
新知再探!
在两个命题中,如果第一个命题的条件和结论,分别是另一个命题的结论和条件,那么这两个命题叫做互逆命题.
一个命题是真命题,它的逆命题不一定是真命题哦!
原命题:如果两个角是对顶角,那么它们相等;
逆命题:如果两个角相等,那么它们是对顶角.
真
假
议一议:观察下面两组定理,它们是互逆命题吗?
定理:直角三角形的两个锐角互余.
定理:有两个角互余的三角形是直角三角形.
定理:直角三角形两条直角边的平方和等于斜边的平方.
定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
新知再探!
如果一个定理的逆命题也是定理,那么这两个定理叫做互逆定理,其中的一个定理叫做另一个定理的逆定理.
实战演练!
1.在△ABC中,已知∠A=∠B=45°,BC =3,求AB的长.
2.已知:在△ABC中,AB=13㎝,BC =10㎝,BC边上的中线AD=12㎝.求证:AB=AC.
3.说出下列命题的逆命题,并判断每对命题的真假:
(1) 四边形是多边形;
(2)两直线平行,同旁内角互补;
(3)如果ab=0,那么a=0,b=0.
请同学们先独立思考完成,然后进行交流展示!
提高练习!
2.如图,在直角△ABC中,D为斜边AB的中点,DE⊥DF,而E、F分别在AC和BC上,连接EF,请问AE、EF、BF能否组成直角三角形,给出你的结论并说明理由.
中点
垂直
倍长“类中线”
提高练习!
2.如图,在直角△ABC中,D为斜边AB的中点,DE⊥DF,而E、F分别在AC和BC上,连接EF,请问AE、EF、BF能否组成直角三角形,给出你的结论并说明理由.
剩下的证明过程,相信你能搞定哦!
直角三角形
角的性质
边的性质
勾股定理:直角三角形两条直角边的平方和等于斜边的平方;
逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
定理1:直角三角形的两个锐角互余;
定理2:有两个角互余的三角形是直角三角形
既是互逆命题又是互逆定理
我的收获!
1.教材习题1.5
2.对应练习册
课后练习
宝宝不哭,作业不会太多哦!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
