5.1.2 垂线同步练习(含答案)
图片预览




文档简介
人教版七年级下册5.1.2垂线同步练习
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020秋?德惠市期末)如图,OA⊥OB,若∠1=55°16′,则∠2的度数是( )
A.35°44′ B.34°84′ C.34°74′ D.34°44′
2.(2020?陕西)如图,AC⊥BC,直线EF经过点C,若∠1=35°,则∠2的大小为( )
A.65° B.55° C.45° D.35°
3.(2020春?丛台区校级月考)如果直线ON⊥直线a,直线OM⊥直线a,那么OM与ON重合(即O,M,N三点共线),其理由是( )
A.两点确定一条直线
B.在同一平面内,过两点有且只有一条直线与已知直线垂直
C.在同一平面内,过一点有且只有一条直线与已知直线垂直
D.两点之间,线段最短
4.(2020春?孝义市期末)下列各图中,过直线l外的点P画直线l的垂线,三角尺操作正确的是( )
A. B.
C. D.
5.(2020春?江汉区月考)如图,AD⊥AC交BC的延长线于点D,AE⊥BC交BC的延长线于点E,CF⊥AB于点F,则图中能表示点A到直线BC的距离的是( )
A.AD的长度 B.AE的长度 C.AC的长度 D.CF的长度
6.(2020春?河西区期中)如图所示,在△ABC中,AE⊥BD,点A到直线BD的距离指( )
A.线段AB的长 B.线段AD的长 C.线段ED的长 D.线段AE的长
7.(2020春?长安区校级月考)下列说法:
①两点之间的所有连线中,线段最短;
②在同一平面内,过一点有且只有一条直线与已知直线垂直;
③连接直线外一点与直线上各点的所有线段中,垂线段最短;
④直线外一点到这条直线的垂线段叫做点到直线的距离,其中正确的个数有( )
A.4个 B.3个 C.2个 D.1个
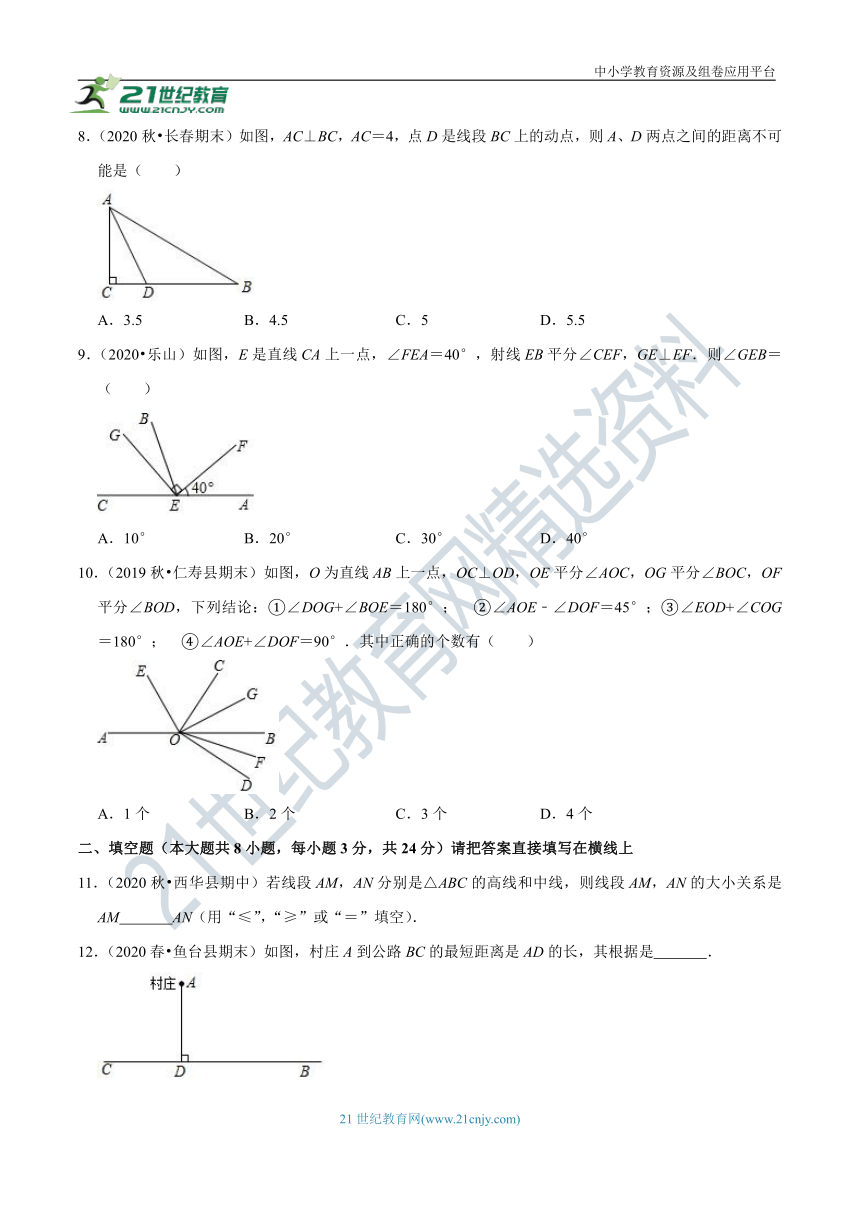
8.(2020秋?长春期末)如图,AC⊥BC,AC=4,点D是线段BC上的动点,则A、D两点之间的距离不可能是( )
A.3.5 B.4.5 C.5 D.5.5
9.(2020?乐山)如图,E是直线CA上一点,∠FEA=40°,射线EB平分∠CEF,GE⊥EF.则∠GEB=( )
A.10° B.20° C.30° D.40°
10.(2019秋?仁寿县期末)如图,O为直线AB上一点,OC⊥OD,OE平分∠AOC,OG平分∠BOC,OF平分∠BOD,下列结论:①∠DOG+∠BOE=180°; ②∠AOE﹣∠DOF=45°;③∠EOD+∠COG=180°; ④∠AOE+∠DOF=90°.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020秋?西华县期中)若线段AM,AN分别是△ABC的高线和中线,则线段AM,AN的大小关系是AM AN(用“≤”,“≥”或“=”填空).
12.(2020春?鱼台县期末)如图,村庄A到公路BC的最短距离是AD的长,其根据是 .
13.(2020秋?绿园区期末)如图,AB⊥l1,AC⊥l2,已知AB=4,BC=3,AC=5,则点A到直线l1的距离是 .
14.(2020春?东城区校级期末)如图,∠C=90°,线段AB=15cm,线段AD=12cm,线段AC=9cm,则点A到BC的距离为 cm.
15.(2020春?岳阳期末)如图,在三角形ABC中,∠ABC=90°,BD⊥AC,垂足为点D,AB=5,BC=12,AC=13,下列结论正确的是 .(写出所有正确结论的序号)
①∠ADB=90°;
②∠A=∠DBC;
③点C到直线BD的距离为线段CB的长度;
④点B到直线AC的距离为6013.
16.(2020春?顺庆区校级月考)如图所示,∠BAC=90°,AD⊥BC,则下列结论中,正确的为 (填序号).
①点A到BC的距离是线段AD的长度;
②线段AB的长度是点B到AC的距离;
③点C到AB的垂线段是线段AB.
17.(2020秋?绿园区期末)如图,直线AB、CD相交于点O,OE⊥AB于点O,且∠COE=48°,则∠AOD为 .
18.(2020秋?南岗区校级期中)已知,∠AOB和∠BOC互为邻补角,且∠BOC:∠AOB=4:1,射线OD平分∠AOB,射线OE⊥OD,则∠BOE= .
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020春?赣州期末)如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
20.(2020春?孟村县期中)如图,AB、CD、NE相交于点O,OM平分∠BOD,∠MON=90°,∠AOC=50°
(1)线段 的长度表示点M到NE的距离;
(2)比较MN与MO的大小(用“<”号连接): ,并说明理由: ;
(3)求∠AON的度数.
21.(2020秋?长春期末)如图,直线AB与直线MN相交,交点为O,OC⊥AB,OA平分∠MOD,若∠BON=20°,求∠COD的度数.
22.(2019秋?海曙区期末)如图,直线AB,CD相交于点O,OD平分∠BOE,OF平分∠AOE.
(1)证明:OD⊥OF.
(2)若∠BOD=28°,找出∠BOD的补角,并求出∠BOF的度数.
23.(2019秋?姜堰区期末)如图,直线AB、CD相交于点O,OM⊥AB,∠1=∠2.
(1)求∠NOD的度数;
(2)若∠AOD=3∠1,求∠AOC和∠MOD的度数.
24.(2019秋?市中区期末)将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起.
(1)如图(1),若∠BOD=35°,则∠AOC= ;若∠AOC=135°,则∠BOD= ;(直接写出结论即可)
(2)如图(2),若∠AOC=140°,则∠BOD= ;(直接写出结论即可)
(3)猜想∠AOC与∠BOD的大小关系,并结合图(1)说明理由;
(4)三角尺AOB不动,将三角尺COD的OD边与OA边重合,然后绕点O按顺时针或逆时针方向任意转动一个角度,当锐角∠AOD等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠AOD角度所有可能的值,不用说明理由.
答案
一、选择题
1.D.2.B.3.C.4.C.5.B.6.D.7.B.8.A.9.B.10.C.
二、填空题
11.≤.
12.垂线段最短.
13.4.
14.9.
15.①②④.
16.①②.
17.138°.
18.72°或108°.
三、解答题
19.【解析】如图所示
(1)沿AB走,两点之间线段最短;
(2)沿AC走,垂线段最短;
(3)沿BD走,垂线段最短.
20.【解析】(1)线段MO的长度表示点M到NE的距离;
(2)比较MN与MO的大小为:MO<MN,是因为垂线段最短;
(3)∵∠BOD=∠AOC=50°,OM平分∠BOD,
∴∠BOM=25°,
∴∠AON=180°﹣∠BOM﹣∠MON=180°﹣25°﹣90°=65°.
故答案为:MO;MO<MN;垂线段最短.
21.【解析】∵∠BON=20°,
∴∠AOM=20°,
∵OA平分∠MOD,
∴∠AOD=∠MOA=20°,
∵OC⊥AB,
∴∠AOC=90°,
∴∠COD=90°﹣20°=70°.
22.【解析】证明:(1)∵OD平分∠BOE,OF平分∠AOE,
∴∠EOF=12∠AOE,∠EOD=12∠EOB,
∵∠AOE+∠EOB=180°,
∴∠FOD=∠EOF+∠EOD=90°,
∴OD⊥OF;
(2)∵∠BOD=28°,
∴∠AOD=180°﹣∠BOD=180°﹣28°=152°,
∵OD平分∠BOE,
∴∠EOD=∠BOD,
∴∠COE=180°﹣∠EOD=180°﹣28°=152°,
∴∠BOD的补角是∠COE和∠AOD,
∵∠FOD=90°,
∴∠BOF=∠DOF+∠BOD=90°+28°=118°.
23.【解析】证明:(1)∵OM⊥AB,
∴∠AOM=∠BOM=90°,
∴∠1+∠AOC=90°,
∵∠1=∠2,
∴∠2+∠AOC=90°,
即∠CON=90°,
∴∠NOD=180°﹣∠CON=180°﹣90°=90°;
(2)∵∠AOD=3∠1,
∴∠NOD=2∠1=90°,
解得:∠1=45°,
∴∠AOC=∠AOM﹣∠1=90°﹣45°=45°;
∴∠BOD=90°﹣45°=45°,
∴∠MOD=∠BOD+∠BOM=45°+90°=135°.
故答案为:(1)90°; (2)45°,135°.
24.【解析】(1)若∠BOD=35°,
∵∠AOB=∠COD=90°,
∴∠AOC=∠AOB+∠COD﹣∠BOD=90°+90°﹣35°=145°,
若∠AOC=135°,
则∠BOD=∠AOB+∠COD﹣∠AOC=90°+90°﹣135°=45°;
故答案为:145°;45°;
(2)如图2,若∠AOC=140°,
则∠BOD=360°﹣∠AOC﹣∠AOB﹣∠COD
=360°﹣140°﹣90°﹣90°
=40°;
故答案为:40°;
(3)∠AOC与∠BOD互补.
∵∠AOB=∠COD=90°,
∴∠AOD+∠BOD+∠BOD+∠BOC=180°.
∵∠AOD+∠BOD+∠BOC=∠AOC,
∴∠AOC+∠BOD=180°,
即∠AOC与∠BOD互补.
(4)OD⊥AB时,∠AOD=30°,
CD⊥OB时,∠AOD=45°,
CD⊥AB时,∠AOD=75°,
OC⊥AB时,∠AOD=60°,
即∠AOD角度所有可能的值为:30°、45°、60°、75°.
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020秋?德惠市期末)如图,OA⊥OB,若∠1=55°16′,则∠2的度数是( )
A.35°44′ B.34°84′ C.34°74′ D.34°44′
2.(2020?陕西)如图,AC⊥BC,直线EF经过点C,若∠1=35°,则∠2的大小为( )
A.65° B.55° C.45° D.35°
3.(2020春?丛台区校级月考)如果直线ON⊥直线a,直线OM⊥直线a,那么OM与ON重合(即O,M,N三点共线),其理由是( )
A.两点确定一条直线
B.在同一平面内,过两点有且只有一条直线与已知直线垂直
C.在同一平面内,过一点有且只有一条直线与已知直线垂直
D.两点之间,线段最短
4.(2020春?孝义市期末)下列各图中,过直线l外的点P画直线l的垂线,三角尺操作正确的是( )
A. B.
C. D.
5.(2020春?江汉区月考)如图,AD⊥AC交BC的延长线于点D,AE⊥BC交BC的延长线于点E,CF⊥AB于点F,则图中能表示点A到直线BC的距离的是( )
A.AD的长度 B.AE的长度 C.AC的长度 D.CF的长度
6.(2020春?河西区期中)如图所示,在△ABC中,AE⊥BD,点A到直线BD的距离指( )
A.线段AB的长 B.线段AD的长 C.线段ED的长 D.线段AE的长
7.(2020春?长安区校级月考)下列说法:
①两点之间的所有连线中,线段最短;
②在同一平面内,过一点有且只有一条直线与已知直线垂直;
③连接直线外一点与直线上各点的所有线段中,垂线段最短;
④直线外一点到这条直线的垂线段叫做点到直线的距离,其中正确的个数有( )
A.4个 B.3个 C.2个 D.1个
8.(2020秋?长春期末)如图,AC⊥BC,AC=4,点D是线段BC上的动点,则A、D两点之间的距离不可能是( )
A.3.5 B.4.5 C.5 D.5.5
9.(2020?乐山)如图,E是直线CA上一点,∠FEA=40°,射线EB平分∠CEF,GE⊥EF.则∠GEB=( )
A.10° B.20° C.30° D.40°
10.(2019秋?仁寿县期末)如图,O为直线AB上一点,OC⊥OD,OE平分∠AOC,OG平分∠BOC,OF平分∠BOD,下列结论:①∠DOG+∠BOE=180°; ②∠AOE﹣∠DOF=45°;③∠EOD+∠COG=180°; ④∠AOE+∠DOF=90°.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020秋?西华县期中)若线段AM,AN分别是△ABC的高线和中线,则线段AM,AN的大小关系是AM AN(用“≤”,“≥”或“=”填空).
12.(2020春?鱼台县期末)如图,村庄A到公路BC的最短距离是AD的长,其根据是 .
13.(2020秋?绿园区期末)如图,AB⊥l1,AC⊥l2,已知AB=4,BC=3,AC=5,则点A到直线l1的距离是 .
14.(2020春?东城区校级期末)如图,∠C=90°,线段AB=15cm,线段AD=12cm,线段AC=9cm,则点A到BC的距离为 cm.
15.(2020春?岳阳期末)如图,在三角形ABC中,∠ABC=90°,BD⊥AC,垂足为点D,AB=5,BC=12,AC=13,下列结论正确的是 .(写出所有正确结论的序号)
①∠ADB=90°;
②∠A=∠DBC;
③点C到直线BD的距离为线段CB的长度;
④点B到直线AC的距离为6013.
16.(2020春?顺庆区校级月考)如图所示,∠BAC=90°,AD⊥BC,则下列结论中,正确的为 (填序号).
①点A到BC的距离是线段AD的长度;
②线段AB的长度是点B到AC的距离;
③点C到AB的垂线段是线段AB.
17.(2020秋?绿园区期末)如图,直线AB、CD相交于点O,OE⊥AB于点O,且∠COE=48°,则∠AOD为 .
18.(2020秋?南岗区校级期中)已知,∠AOB和∠BOC互为邻补角,且∠BOC:∠AOB=4:1,射线OD平分∠AOB,射线OE⊥OD,则∠BOE= .
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020春?赣州期末)如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
20.(2020春?孟村县期中)如图,AB、CD、NE相交于点O,OM平分∠BOD,∠MON=90°,∠AOC=50°
(1)线段 的长度表示点M到NE的距离;
(2)比较MN与MO的大小(用“<”号连接): ,并说明理由: ;
(3)求∠AON的度数.
21.(2020秋?长春期末)如图,直线AB与直线MN相交,交点为O,OC⊥AB,OA平分∠MOD,若∠BON=20°,求∠COD的度数.
22.(2019秋?海曙区期末)如图,直线AB,CD相交于点O,OD平分∠BOE,OF平分∠AOE.
(1)证明:OD⊥OF.
(2)若∠BOD=28°,找出∠BOD的补角,并求出∠BOF的度数.
23.(2019秋?姜堰区期末)如图,直线AB、CD相交于点O,OM⊥AB,∠1=∠2.
(1)求∠NOD的度数;
(2)若∠AOD=3∠1,求∠AOC和∠MOD的度数.
24.(2019秋?市中区期末)将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起.
(1)如图(1),若∠BOD=35°,则∠AOC= ;若∠AOC=135°,则∠BOD= ;(直接写出结论即可)
(2)如图(2),若∠AOC=140°,则∠BOD= ;(直接写出结论即可)
(3)猜想∠AOC与∠BOD的大小关系,并结合图(1)说明理由;
(4)三角尺AOB不动,将三角尺COD的OD边与OA边重合,然后绕点O按顺时针或逆时针方向任意转动一个角度,当锐角∠AOD等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠AOD角度所有可能的值,不用说明理由.
答案
一、选择题
1.D.2.B.3.C.4.C.5.B.6.D.7.B.8.A.9.B.10.C.
二、填空题
11.≤.
12.垂线段最短.
13.4.
14.9.
15.①②④.
16.①②.
17.138°.
18.72°或108°.
三、解答题
19.【解析】如图所示
(1)沿AB走,两点之间线段最短;
(2)沿AC走,垂线段最短;
(3)沿BD走,垂线段最短.
20.【解析】(1)线段MO的长度表示点M到NE的距离;
(2)比较MN与MO的大小为:MO<MN,是因为垂线段最短;
(3)∵∠BOD=∠AOC=50°,OM平分∠BOD,
∴∠BOM=25°,
∴∠AON=180°﹣∠BOM﹣∠MON=180°﹣25°﹣90°=65°.
故答案为:MO;MO<MN;垂线段最短.
21.【解析】∵∠BON=20°,
∴∠AOM=20°,
∵OA平分∠MOD,
∴∠AOD=∠MOA=20°,
∵OC⊥AB,
∴∠AOC=90°,
∴∠COD=90°﹣20°=70°.
22.【解析】证明:(1)∵OD平分∠BOE,OF平分∠AOE,
∴∠EOF=12∠AOE,∠EOD=12∠EOB,
∵∠AOE+∠EOB=180°,
∴∠FOD=∠EOF+∠EOD=90°,
∴OD⊥OF;
(2)∵∠BOD=28°,
∴∠AOD=180°﹣∠BOD=180°﹣28°=152°,
∵OD平分∠BOE,
∴∠EOD=∠BOD,
∴∠COE=180°﹣∠EOD=180°﹣28°=152°,
∴∠BOD的补角是∠COE和∠AOD,
∵∠FOD=90°,
∴∠BOF=∠DOF+∠BOD=90°+28°=118°.
23.【解析】证明:(1)∵OM⊥AB,
∴∠AOM=∠BOM=90°,
∴∠1+∠AOC=90°,
∵∠1=∠2,
∴∠2+∠AOC=90°,
即∠CON=90°,
∴∠NOD=180°﹣∠CON=180°﹣90°=90°;
(2)∵∠AOD=3∠1,
∴∠NOD=2∠1=90°,
解得:∠1=45°,
∴∠AOC=∠AOM﹣∠1=90°﹣45°=45°;
∴∠BOD=90°﹣45°=45°,
∴∠MOD=∠BOD+∠BOM=45°+90°=135°.
故答案为:(1)90°; (2)45°,135°.
24.【解析】(1)若∠BOD=35°,
∵∠AOB=∠COD=90°,
∴∠AOC=∠AOB+∠COD﹣∠BOD=90°+90°﹣35°=145°,
若∠AOC=135°,
则∠BOD=∠AOB+∠COD﹣∠AOC=90°+90°﹣135°=45°;
故答案为:145°;45°;
(2)如图2,若∠AOC=140°,
则∠BOD=360°﹣∠AOC﹣∠AOB﹣∠COD
=360°﹣140°﹣90°﹣90°
=40°;
故答案为:40°;
(3)∠AOC与∠BOD互补.
∵∠AOB=∠COD=90°,
∴∠AOD+∠BOD+∠BOD+∠BOC=180°.
∵∠AOD+∠BOD+∠BOC=∠AOC,
∴∠AOC+∠BOD=180°,
即∠AOC与∠BOD互补.
(4)OD⊥AB时,∠AOD=30°,
CD⊥OB时,∠AOD=45°,
CD⊥AB时,∠AOD=75°,
OC⊥AB时,∠AOD=60°,
即∠AOD角度所有可能的值为:30°、45°、60°、75°.
