2020-2021学年 苏科版九年级数学下册 第七章 锐角三角函数 单元检测试题(word有答案)
文档属性
| 名称 | 2020-2021学年 苏科版九年级数学下册 第七章 锐角三角函数 单元检测试题(word有答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 148.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 00:00:00 | ||
图片预览



文档简介
1031240010337800第七章 锐角三角函数 单元检测试题
班级:_____________姓名:_____________
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
1. 在Rt△ABC中,∠C=90?,AB=5,BC=3,则sinA的值为(? ? ? ? )
A.34 B.43 C.35 D.45?
2. 如图,在Rt△ABC中,∠BAC=90?,延长斜边BC到点D,使CD=12BC,连接AD,若sinB=45,则tan∠CAD的值(? ? ? ? )
A.33 B. 32 C.13 D. 14 ?
3. 如图,小正方形的边长均为1,有格点△ABC,则sinC=( )
A.23 B.55 C.12 D.22
4. 在Rt△ABC中,∠C=90?,下列式子中最大的一个是( )
A.tanA+cotA B.sinA+cosA C.tanA+cosA D.cotA+sinA
5. 已知∠A为锐角,且cosA=1213,则sinA等于( )
A.1312 B.513 C.512 D.125?
6. 若斜坡的坡比为1:33,则斜坡的坡角等于( )
A.30? B.45? C.50? D.60?
?7. 在Rt△ABC中,∠C=90?,cosA=35,则sinB的值为(? ? ? ? )
A.54 B.45 C.53 D.35?
8. 如图所示,渔船在A处看到灯塔C在北偏东60?方向上,渔船正向东方向航行了12海里到达B处,在B处看到灯塔C在正北方向上,这时渔船与灯塔C的距离是( )
A.123海里 B.63海里 C.6海里 D.43海里?
9. 已知BD是△ABC的中线,AC=6,且∠ADB=45?,∠C=30?,则AB=( )
A.6 B.23 C.32 D.6?
10. 如图,已知△ABC中,∠B=90?,AB=3,BC=3,OA=OC=6,则∠OAB的度数为( )
A.10? B.15? C.20? D.25?
二、 填空题 (本题共计 11 小题 ,每题 3 分 ,共计33分 , ) ?
11. 已知三角形的两条边长分别是3cm和4cm,一个内角为40?,那么满足这一条件且彼此不全等的三角形共有________个. ?
12. 在△ABC中, ∠C=90?,若sinB=513,则cosA=________.
13. 如果∠A为锐角,且cosA=14,那么∠A的范围是________.
?
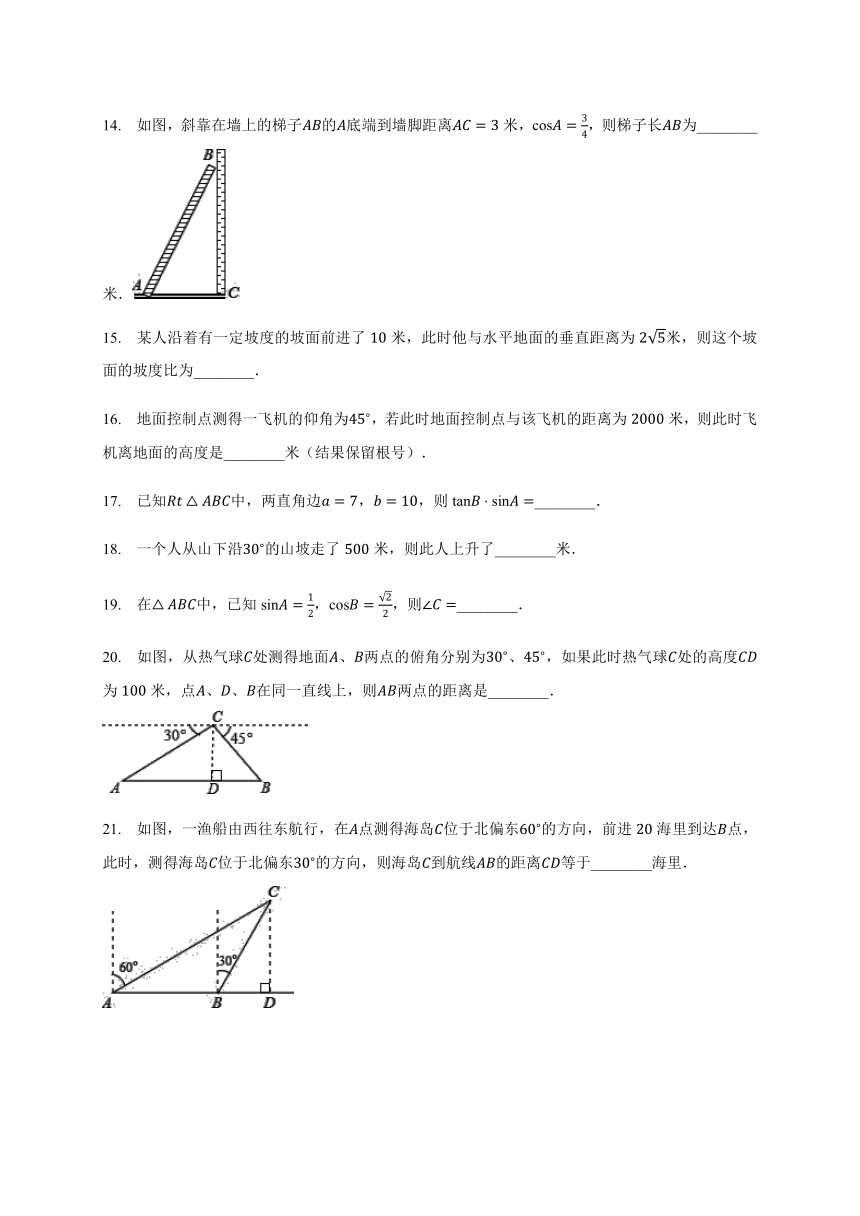
14. 如图,斜靠在墙上的梯子AB的A底端到墙脚距离AC=3米,cosA=34,则梯子长AB为________米. ?
15. 某人沿着有一定坡度的坡面前进了10米,此时他与水平地面的垂直距离为25米,则这个坡面的坡度比为________.
16. 地面控制点测得一飞机的仰角为45?,若此时地面控制点与该飞机的距离为2000米,则此时飞机离地面的高度是________米(结果保留根号). ?
17. 已知Rt△ABC中,两直角边a=7,b=10,则tanB?sinA=________. ?
18. 一个人从山下沿30?的山坡走了500米,则此人上升了________米.
19. 在△ABC中,已知sinA=12,cosB=22,则∠C=________.
20. 如图,从热气球C处测得地面A、B两点的俯角分别为30?、45?,如果此时热气球C处的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是________.
21. 如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60?的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30?的方向,则海岛C到航线AB的距离CD等于________海里.
三、 解答题 (本题共计 5 小题 ,共计57分 , ) ?
22. 化简下列各式:
(1)cos228?-2cos28?+1+|sin60?-cos28?|.
(2)sin45?1+sin60?-cos45?1-sin60?+2(sin30?-cos30?)2.
?
23. 在Rt△ABC中,∠C=90?,BC=5,sinA=513,求AC的长.
?
24. 如图,甲、乙两栋高楼的水平距离BD为90米,从甲楼顶部C点测得乙楼顶部A点的仰角α为30?,测得乙楼底部B点的俯角β为60?,求甲、乙两栋高楼各有多高?(计算过程和结果都不取近似值)
?
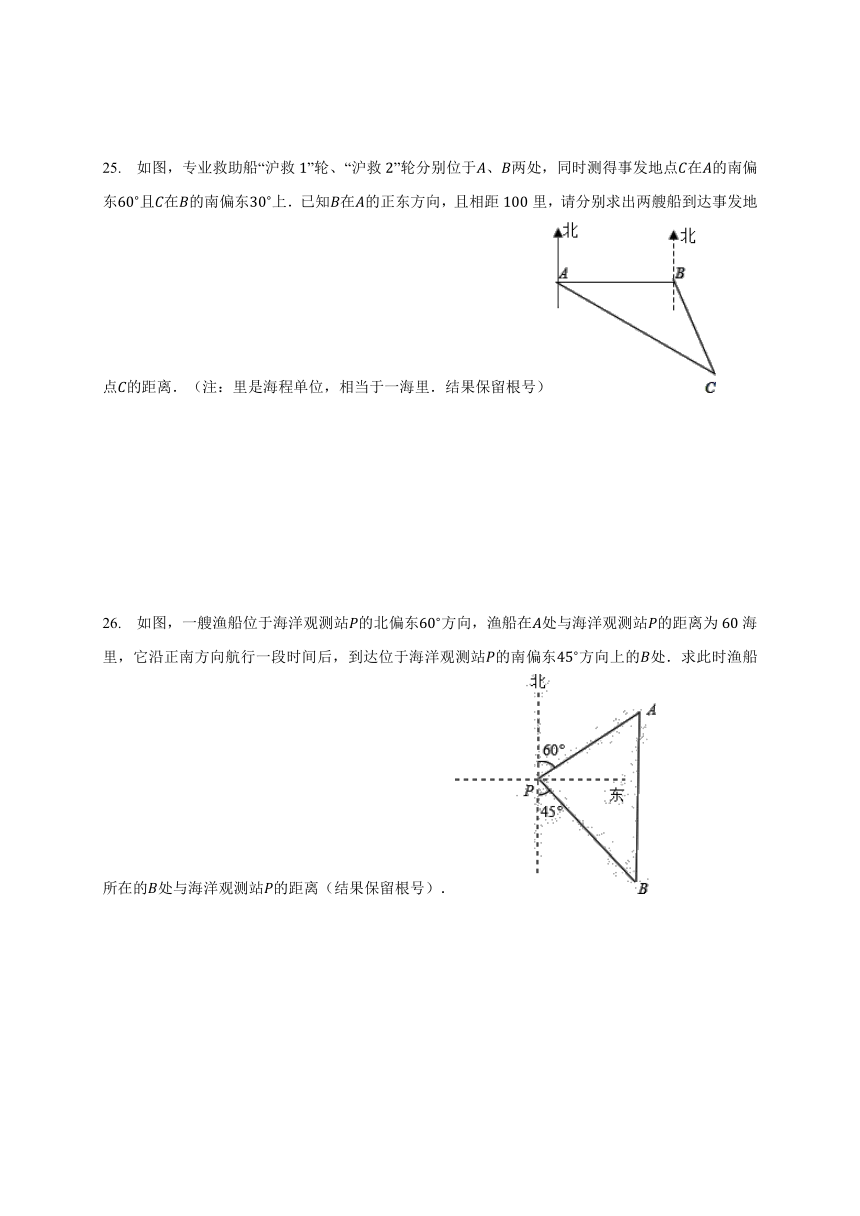
25. 如图,专业救助船“沪救1”轮、“沪救2”轮分别位于A、B两处,同时测得事发地点C在A的南偏东60?且C在B的南偏东30?上.已知B在A的正东方向,且相距100里,请分别求出两艘船到达事发地点C的距离.(注:里是海程单位,相当于一海里.结果保留根号)
?
26. 如图,一艘渔船位于海洋观测站P的北偏东60?方向,渔船在A处与海洋观测站P的距离为60海里,它沿正南方向航行一段时间后,到达位于海洋观测站P的南偏东45?方向上的B处.求此时渔船所在的B处与海洋观测站P的距离(结果保留根号).
参考答案与试题解析
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
【解答】
解:在Rt△ABC中,∠C=90?,AB=5,BC=3,如图:
则sinA=BCAB=35.
故选C.
2.
【答案】
D
【解答】
解:如图,延长AC,过点D作DE⊥CE,垂足为E,
∵ sinB=45,即ACBC=45,
∴ 设AC=4x,则BC=5x,
∵ ∠ACB=∠ECD,∠ABC=∠EDC,
∴ △CDE∽△CBA,
∴ CEAC=DEAB=CDBC=12,
∴ DE=32x,CE=2x,
∴ AE=6x,
∴ tan∠CAD=EDAE=14.
故选D.
3.
【答案】
B
【解答】
解:如图,连接BD,
由正方形的性质可知,∠CDB=90?,BD=2,BC=10,
则sinC=BDBC=55,
故选:B.
4.
【答案】
A
【解答】
解:∵ 在Rt△ABC中,∠C=90?,
∴ 0?<∠A<90?,
∵ tanA=sinAcosA,
0∴ tanA>sinA,
∵ cotA=cosAsinA,
∴ cotA>cosA,
故:tanA+cotA>sinA+cosA,tanA+cotA>tanA+cosA,tanA+cotA>cotA+sinA,
则式子中最大的一个是tanA+cotA.
故选:A.
5.
【答案】
B
【解答】
解:由cosA=1213知,
如果设b=12x,则c=13x,结合a2+b2=c2得a=5x;
∴ sinA=ac=5x13x=513.
故sinA=513,
故选B.
6.
【答案】
D
【解答】
∵ 斜坡的坡比为1:33,设坡角为α,
∴ tanα=133=3,
∴ α=60?.
7.
【答案】
D
【解答】
解:在Rt△ABC中,∠C=90?,cosA=35,
则sinB=cosA=35.
故选D.
8.
【答案】
D
【解答】
解:由已知得:∠BAC=90?-60?=30?,
在直角三角形ABC中,
BC=AB?tan30?
=12×33
=43(海里).
故选:D.
9.
【答案】
C
【解答】
过点B作BE⊥AC交AC于点E.如下图
设BE=x,
∵ ∠BDA=45?,∠C=30?,
∴ DE=x,BC=2x,
∵ tan∠C=BECE,
∴ x3+x=tan30?,
∴ 3x=(3+x)3,解得x=3+332,
在Rt△ABE中,AE=DE-AD=3+332-3=33-32,
由勾股定理得:AB2=BE2+AE2,AB=(3+332)2+(33-32)2=32.
10.
【答案】
B
【解答】
解:∵ AC2=AB2+BC2=32+(3)2=12,
AO2+CO2=(6)2+(6)2=12,
∴ AC2=AO2+OC2,
∴ ∠O=90?,
∵ OA=OC,
∴ ∠OAC=45?,
在Rt△ACB中,
∵ tan∠BAC=33,
∴ ∠BAC=30?,
∴ ∠OAB=45?-30?=15?,
故选B.
二、 填空题 (本题共计 11 小题 ,每题 3 分 ,共计33分 )
11.
【答案】
4
【解答】
解:如图满足这样条件的三角形有4个,分别是:
a=3,b=4,∠C=40?;a=3,∠B=40?b=4;a=3,b=4,∠A=40?有2解.
先画一条直线,确定一点A作40?的角,取4cm,得到C,以C为圆心,3cm为半径,交直线于2点,B和B1,符合条件三角形有2个△ABC和△AB1C.
故答案为:4.
12.
【答案】
513
【解答】
解:在△ABC中,∠C=90?,
所以∠A+∠B=90?,
则cosA=sinB=513.
故答案为:513.
13.
【答案】
60?<∠A<90?
【解答】
解:∵ cos60?=12,
14<12,
而锐角的余弦随角度的增大而减小,
故锐角A的范围是60?<∠A<90?.
故答案为:60?<∠A<90?.
14.
【答案】
4
【解答】
解:∵ AC=3米,cosA=34,∠C=90?,
∴ cosA=ACAB=34=3AB,
解得:AB=4,
即梯子长AB为4米.
故答案为:4.
15.
【答案】
1:2
【解答】
解:∵ 某人沿着有一定坡度的坡面前进了10米.此时他与水平地面的垂直距离为25米,
根据勾股定理可以求出他前进的水平距离为45米.
所以这个坡面的坡度比为25:45=1:2.
16.
【答案】
10002
【解答】
解:如图所示:
由题意得,∠CAB=45?,AC=2000m,
则BC=ACsin∠CAB=2000×22=10002m;
即飞机离地面的高度是10002米.
故答案为:10002.
17.
【答案】
10149149
【解答】
解:∵ 在Rt△ABC中,两直角边a=7,b=10
∴ 斜边c=a2+b2=72+102=49+100=149
∴ tanB=ba=107,sinA=ac=7149=7149149
∴ tanB?sinA=107×7149149=10149149
18.
【答案】
250
【解答】
解:由30?所对的直角边是斜边的一半,得此人上升的高度=500÷2=250m.
故答案为250.
19.
【答案】
105?
【解答】
解:∵ sinA=12,cosB=22,
∴ ∠A=30?,∠B=45?,
∴ ∠C=180?-30?-45?=105?.
故答案为:105?.
20.
【答案】
100(3+1)米
【解答】
∵ 从热气球C处测得地面A、B两点的俯角分别为30?、45?,
∴ ∠BCD=90?-45?=45?,∠ACD=90?-30?=60?,
∵ CD⊥AB,CD=100m,
∴ △BCD是等腰直角三角形,
∴ BD=CD=100m,
在Rt△ACD中,
∵ CD=100m,∠ACD=60?,
∴ AD=CD?tan60?=100×3=1003m,
∴ AB=AD+BD=1003+100=100(3+1)m.
21.
【答案】
103
【解答】
根据题意可知∠CAD=30?,∠CBD=60?,
∵ ∠CBD=∠CAD+∠ACB,
∴ ∠CAD=30?=∠ACB,
∴ AB=BC=20海里,
在Rt△CBD中,∠BDC=90?,∠DBC=60?,sin∠DBC=CDBC,
∴ sin60?=CDBC,
∴ CD=20×sin60?=20×32=103海里,
三、 解答题 (本题共计 5 小题 ,每题 10 分 ,共计50分 )
22.
【答案】
解:(1)cos228?-2cos28?+1+|sin60?-cos28?|
=(cs28?-1)2+cos28?-sin60?
=1-cos28?+cos28?-sin60?
=1+32;
(2)sin45?1+sin60?-cos45?1-sin60?+2(sin30?-cos30?)2
=221+32-221-32+2(12-32)2
=22+3-22-3+2(32-12)
=2(2-3)-2(2+3)-62+22
=-562+22.
【解答】
解:(1)cos228?-2cos28?+1+|sin60?-cos28?|
=(cs28?-1)2+cos28?-sin60?
=1-cos28?+cos28?-sin60?
=1+32;
(2)sin45?1+sin60?-cos45?1-sin60?+2(sin30?-cos30?)2
=221+32-221-32+2(12-32)2
=22+3-22-3+2(32-12)
=2(2-3)-2(2+3)-62+22
=-562+22.
23.
【答案】
解:∵ sinA=BCAB=513,BC=5,
∴ AB=13,
根据勾股定理,AC=AB2-BC2=12.
【解答】
解:∵ sinA=BCAB=513,BC=5,
∴ AB=13,
根据勾股定理,AC=AB2-BC2=12.
24.
【答案】
甲楼高为903米,乙楼高为1203米.
【解答】
解:作CE⊥AB于点E.
∵ CE?//?DB,CD?//?AB,且∠CDB=90?,
∴ 四边形BECD是矩形.
∴ CD=BE,CE=BD.
在Rt△BCE中,β=60?,CE=BD=90米.
∵ tanβ=BECE,
∴ BE=CE?tanβ=90×tan60?=903(米).
∴ CD=BE=903(米).
在Rt△ACE中,α=30?,CE=90米.
∵ tanα=AECE,
∴ AE=CE?tanα=90×tan30?=90×33=303(米).
∴ AB=AE+BE=303+903=1203(米).
25.
【答案】
A船到达事发地点C的距离是1003里,B船到达事发地点C的距离是100里.
【解答】
解:作BG⊥AC于G,
∵ 点C在A的南偏东60?,
∴ ∠A=90?-60?=30?,
∵ C在B的南偏东30?,
∴ ∠ABC=120?,
∴ ∠C=30?,
∴ BC=AB=100里,
∴ BG=BC?sin30?=50里,
CG=BC?cos30?=503里,
∴ AC=2CG=1003里.
26.
【答案】
当渔船位于P南偏东45?方向时,渔船与P的距离是306海里.
【解答】
解:过点P作PC⊥AB,垂足为C,
根据题意可得出:∠APC=30?,∠BPC=45?,AP=60,
在Rt△APC中,∵ cos∠APC=PCPA,
∴ PC=PA?cos∠APC=303,
在Rt△PCB中,∵ cos∠BPC=PCPB,
∴ PB=PCcos∠BPC=303cos45?=306.
班级:_____________姓名:_____________
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
1. 在Rt△ABC中,∠C=90?,AB=5,BC=3,则sinA的值为(? ? ? ? )
A.34 B.43 C.35 D.45?
2. 如图,在Rt△ABC中,∠BAC=90?,延长斜边BC到点D,使CD=12BC,连接AD,若sinB=45,则tan∠CAD的值(? ? ? ? )
A.33 B. 32 C.13 D. 14 ?
3. 如图,小正方形的边长均为1,有格点△ABC,则sinC=( )
A.23 B.55 C.12 D.22
4. 在Rt△ABC中,∠C=90?,下列式子中最大的一个是( )
A.tanA+cotA B.sinA+cosA C.tanA+cosA D.cotA+sinA
5. 已知∠A为锐角,且cosA=1213,则sinA等于( )
A.1312 B.513 C.512 D.125?
6. 若斜坡的坡比为1:33,则斜坡的坡角等于( )
A.30? B.45? C.50? D.60?
?7. 在Rt△ABC中,∠C=90?,cosA=35,则sinB的值为(? ? ? ? )
A.54 B.45 C.53 D.35?
8. 如图所示,渔船在A处看到灯塔C在北偏东60?方向上,渔船正向东方向航行了12海里到达B处,在B处看到灯塔C在正北方向上,这时渔船与灯塔C的距离是( )
A.123海里 B.63海里 C.6海里 D.43海里?
9. 已知BD是△ABC的中线,AC=6,且∠ADB=45?,∠C=30?,则AB=( )
A.6 B.23 C.32 D.6?
10. 如图,已知△ABC中,∠B=90?,AB=3,BC=3,OA=OC=6,则∠OAB的度数为( )
A.10? B.15? C.20? D.25?
二、 填空题 (本题共计 11 小题 ,每题 3 分 ,共计33分 , ) ?
11. 已知三角形的两条边长分别是3cm和4cm,一个内角为40?,那么满足这一条件且彼此不全等的三角形共有________个. ?
12. 在△ABC中, ∠C=90?,若sinB=513,则cosA=________.
13. 如果∠A为锐角,且cosA=14,那么∠A的范围是________.
?
14. 如图,斜靠在墙上的梯子AB的A底端到墙脚距离AC=3米,cosA=34,则梯子长AB为________米. ?
15. 某人沿着有一定坡度的坡面前进了10米,此时他与水平地面的垂直距离为25米,则这个坡面的坡度比为________.
16. 地面控制点测得一飞机的仰角为45?,若此时地面控制点与该飞机的距离为2000米,则此时飞机离地面的高度是________米(结果保留根号). ?
17. 已知Rt△ABC中,两直角边a=7,b=10,则tanB?sinA=________. ?
18. 一个人从山下沿30?的山坡走了500米,则此人上升了________米.
19. 在△ABC中,已知sinA=12,cosB=22,则∠C=________.
20. 如图,从热气球C处测得地面A、B两点的俯角分别为30?、45?,如果此时热气球C处的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是________.
21. 如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60?的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30?的方向,则海岛C到航线AB的距离CD等于________海里.
三、 解答题 (本题共计 5 小题 ,共计57分 , ) ?
22. 化简下列各式:
(1)cos228?-2cos28?+1+|sin60?-cos28?|.
(2)sin45?1+sin60?-cos45?1-sin60?+2(sin30?-cos30?)2.
?
23. 在Rt△ABC中,∠C=90?,BC=5,sinA=513,求AC的长.
?
24. 如图,甲、乙两栋高楼的水平距离BD为90米,从甲楼顶部C点测得乙楼顶部A点的仰角α为30?,测得乙楼底部B点的俯角β为60?,求甲、乙两栋高楼各有多高?(计算过程和结果都不取近似值)
?
25. 如图,专业救助船“沪救1”轮、“沪救2”轮分别位于A、B两处,同时测得事发地点C在A的南偏东60?且C在B的南偏东30?上.已知B在A的正东方向,且相距100里,请分别求出两艘船到达事发地点C的距离.(注:里是海程单位,相当于一海里.结果保留根号)
?
26. 如图,一艘渔船位于海洋观测站P的北偏东60?方向,渔船在A处与海洋观测站P的距离为60海里,它沿正南方向航行一段时间后,到达位于海洋观测站P的南偏东45?方向上的B处.求此时渔船所在的B处与海洋观测站P的距离(结果保留根号).
参考答案与试题解析
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
【解答】
解:在Rt△ABC中,∠C=90?,AB=5,BC=3,如图:
则sinA=BCAB=35.
故选C.
2.
【答案】
D
【解答】
解:如图,延长AC,过点D作DE⊥CE,垂足为E,
∵ sinB=45,即ACBC=45,
∴ 设AC=4x,则BC=5x,
∵ ∠ACB=∠ECD,∠ABC=∠EDC,
∴ △CDE∽△CBA,
∴ CEAC=DEAB=CDBC=12,
∴ DE=32x,CE=2x,
∴ AE=6x,
∴ tan∠CAD=EDAE=14.
故选D.
3.
【答案】
B
【解答】
解:如图,连接BD,
由正方形的性质可知,∠CDB=90?,BD=2,BC=10,
则sinC=BDBC=55,
故选:B.
4.
【答案】
A
【解答】
解:∵ 在Rt△ABC中,∠C=90?,
∴ 0?<∠A<90?,
∵ tanA=sinAcosA,
0
∵ cotA=cosAsinA,
∴ cotA>cosA,
故:tanA+cotA>sinA+cosA,tanA+cotA>tanA+cosA,tanA+cotA>cotA+sinA,
则式子中最大的一个是tanA+cotA.
故选:A.
5.
【答案】
B
【解答】
解:由cosA=1213知,
如果设b=12x,则c=13x,结合a2+b2=c2得a=5x;
∴ sinA=ac=5x13x=513.
故sinA=513,
故选B.
6.
【答案】
D
【解答】
∵ 斜坡的坡比为1:33,设坡角为α,
∴ tanα=133=3,
∴ α=60?.
7.
【答案】
D
【解答】
解:在Rt△ABC中,∠C=90?,cosA=35,
则sinB=cosA=35.
故选D.
8.
【答案】
D
【解答】
解:由已知得:∠BAC=90?-60?=30?,
在直角三角形ABC中,
BC=AB?tan30?
=12×33
=43(海里).
故选:D.
9.
【答案】
C
【解答】
过点B作BE⊥AC交AC于点E.如下图
设BE=x,
∵ ∠BDA=45?,∠C=30?,
∴ DE=x,BC=2x,
∵ tan∠C=BECE,
∴ x3+x=tan30?,
∴ 3x=(3+x)3,解得x=3+332,
在Rt△ABE中,AE=DE-AD=3+332-3=33-32,
由勾股定理得:AB2=BE2+AE2,AB=(3+332)2+(33-32)2=32.
10.
【答案】
B
【解答】
解:∵ AC2=AB2+BC2=32+(3)2=12,
AO2+CO2=(6)2+(6)2=12,
∴ AC2=AO2+OC2,
∴ ∠O=90?,
∵ OA=OC,
∴ ∠OAC=45?,
在Rt△ACB中,
∵ tan∠BAC=33,
∴ ∠BAC=30?,
∴ ∠OAB=45?-30?=15?,
故选B.
二、 填空题 (本题共计 11 小题 ,每题 3 分 ,共计33分 )
11.
【答案】
4
【解答】
解:如图满足这样条件的三角形有4个,分别是:
a=3,b=4,∠C=40?;a=3,∠B=40?b=4;a=3,b=4,∠A=40?有2解.
先画一条直线,确定一点A作40?的角,取4cm,得到C,以C为圆心,3cm为半径,交直线于2点,B和B1,符合条件三角形有2个△ABC和△AB1C.
故答案为:4.
12.
【答案】
513
【解答】
解:在△ABC中,∠C=90?,
所以∠A+∠B=90?,
则cosA=sinB=513.
故答案为:513.
13.
【答案】
60?<∠A<90?
【解答】
解:∵ cos60?=12,
14<12,
而锐角的余弦随角度的增大而减小,
故锐角A的范围是60?<∠A<90?.
故答案为:60?<∠A<90?.
14.
【答案】
4
【解答】
解:∵ AC=3米,cosA=34,∠C=90?,
∴ cosA=ACAB=34=3AB,
解得:AB=4,
即梯子长AB为4米.
故答案为:4.
15.
【答案】
1:2
【解答】
解:∵ 某人沿着有一定坡度的坡面前进了10米.此时他与水平地面的垂直距离为25米,
根据勾股定理可以求出他前进的水平距离为45米.
所以这个坡面的坡度比为25:45=1:2.
16.
【答案】
10002
【解答】
解:如图所示:
由题意得,∠CAB=45?,AC=2000m,
则BC=ACsin∠CAB=2000×22=10002m;
即飞机离地面的高度是10002米.
故答案为:10002.
17.
【答案】
10149149
【解答】
解:∵ 在Rt△ABC中,两直角边a=7,b=10
∴ 斜边c=a2+b2=72+102=49+100=149
∴ tanB=ba=107,sinA=ac=7149=7149149
∴ tanB?sinA=107×7149149=10149149
18.
【答案】
250
【解答】
解:由30?所对的直角边是斜边的一半,得此人上升的高度=500÷2=250m.
故答案为250.
19.
【答案】
105?
【解答】
解:∵ sinA=12,cosB=22,
∴ ∠A=30?,∠B=45?,
∴ ∠C=180?-30?-45?=105?.
故答案为:105?.
20.
【答案】
100(3+1)米
【解答】
∵ 从热气球C处测得地面A、B两点的俯角分别为30?、45?,
∴ ∠BCD=90?-45?=45?,∠ACD=90?-30?=60?,
∵ CD⊥AB,CD=100m,
∴ △BCD是等腰直角三角形,
∴ BD=CD=100m,
在Rt△ACD中,
∵ CD=100m,∠ACD=60?,
∴ AD=CD?tan60?=100×3=1003m,
∴ AB=AD+BD=1003+100=100(3+1)m.
21.
【答案】
103
【解答】
根据题意可知∠CAD=30?,∠CBD=60?,
∵ ∠CBD=∠CAD+∠ACB,
∴ ∠CAD=30?=∠ACB,
∴ AB=BC=20海里,
在Rt△CBD中,∠BDC=90?,∠DBC=60?,sin∠DBC=CDBC,
∴ sin60?=CDBC,
∴ CD=20×sin60?=20×32=103海里,
三、 解答题 (本题共计 5 小题 ,每题 10 分 ,共计50分 )
22.
【答案】
解:(1)cos228?-2cos28?+1+|sin60?-cos28?|
=(cs28?-1)2+cos28?-sin60?
=1-cos28?+cos28?-sin60?
=1+32;
(2)sin45?1+sin60?-cos45?1-sin60?+2(sin30?-cos30?)2
=221+32-221-32+2(12-32)2
=22+3-22-3+2(32-12)
=2(2-3)-2(2+3)-62+22
=-562+22.
【解答】
解:(1)cos228?-2cos28?+1+|sin60?-cos28?|
=(cs28?-1)2+cos28?-sin60?
=1-cos28?+cos28?-sin60?
=1+32;
(2)sin45?1+sin60?-cos45?1-sin60?+2(sin30?-cos30?)2
=221+32-221-32+2(12-32)2
=22+3-22-3+2(32-12)
=2(2-3)-2(2+3)-62+22
=-562+22.
23.
【答案】
解:∵ sinA=BCAB=513,BC=5,
∴ AB=13,
根据勾股定理,AC=AB2-BC2=12.
【解答】
解:∵ sinA=BCAB=513,BC=5,
∴ AB=13,
根据勾股定理,AC=AB2-BC2=12.
24.
【答案】
甲楼高为903米,乙楼高为1203米.
【解答】
解:作CE⊥AB于点E.
∵ CE?//?DB,CD?//?AB,且∠CDB=90?,
∴ 四边形BECD是矩形.
∴ CD=BE,CE=BD.
在Rt△BCE中,β=60?,CE=BD=90米.
∵ tanβ=BECE,
∴ BE=CE?tanβ=90×tan60?=903(米).
∴ CD=BE=903(米).
在Rt△ACE中,α=30?,CE=90米.
∵ tanα=AECE,
∴ AE=CE?tanα=90×tan30?=90×33=303(米).
∴ AB=AE+BE=303+903=1203(米).
25.
【答案】
A船到达事发地点C的距离是1003里,B船到达事发地点C的距离是100里.
【解答】
解:作BG⊥AC于G,
∵ 点C在A的南偏东60?,
∴ ∠A=90?-60?=30?,
∵ C在B的南偏东30?,
∴ ∠ABC=120?,
∴ ∠C=30?,
∴ BC=AB=100里,
∴ BG=BC?sin30?=50里,
CG=BC?cos30?=503里,
∴ AC=2CG=1003里.
26.
【答案】
当渔船位于P南偏东45?方向时,渔船与P的距离是306海里.
【解答】
解:过点P作PC⊥AB,垂足为C,
根据题意可得出:∠APC=30?,∠BPC=45?,AP=60,
在Rt△APC中,∵ cos∠APC=PCPA,
∴ PC=PA?cos∠APC=303,
在Rt△PCB中,∵ cos∠BPC=PCPB,
∴ PB=PCcos∠BPC=303cos45?=306.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
