2020-2021学年九年级数学人教版下册 第27章:相似 精选提升练习(一)(Word版 含解析)
文档属性
| 名称 | 2020-2021学年九年级数学人教版下册 第27章:相似 精选提升练习(一)(Word版 含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 151.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 00:00:00 | ||
图片预览



文档简介
2020-2021学年人教版九年级数学下册
第27章:相似
精选提升练习(一)
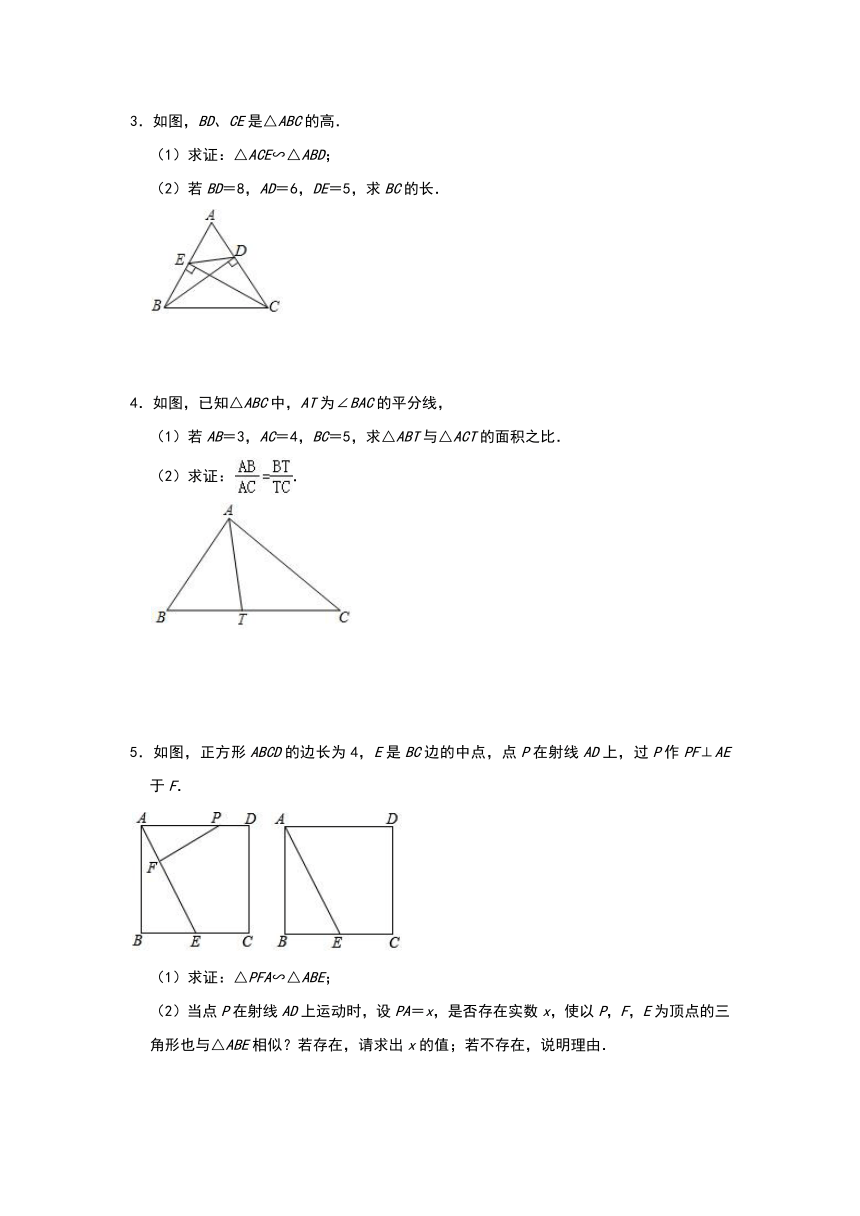
1.在Rt△ABC中,∠ABC=90°,P是线段AC的中点.
(1)如图①,当∠A=30°,且点M,N分别在线段AB,BC上时,∠MPN=90°,写出线段PM与PN的比值,并给予证明;
(2)如图②,当∠A=30°,且点M,N分别在线段AB,BC的延长线上时,∠MPN=90°,线段PM与PN的比值等于
.
2.如图,在△ABC中,点D在边AB上,点E、点F在边AC上,且DE∥BC,=.
(1)求证:DF∥BE;
(2)如果AF=2,EF=4,AB=6,求的值.
3.如图,BD、CE是△ABC的高.
(1)求证:△ACE∽△ABD;
(2)若BD=8,AD=6,DE=5,求BC的长.
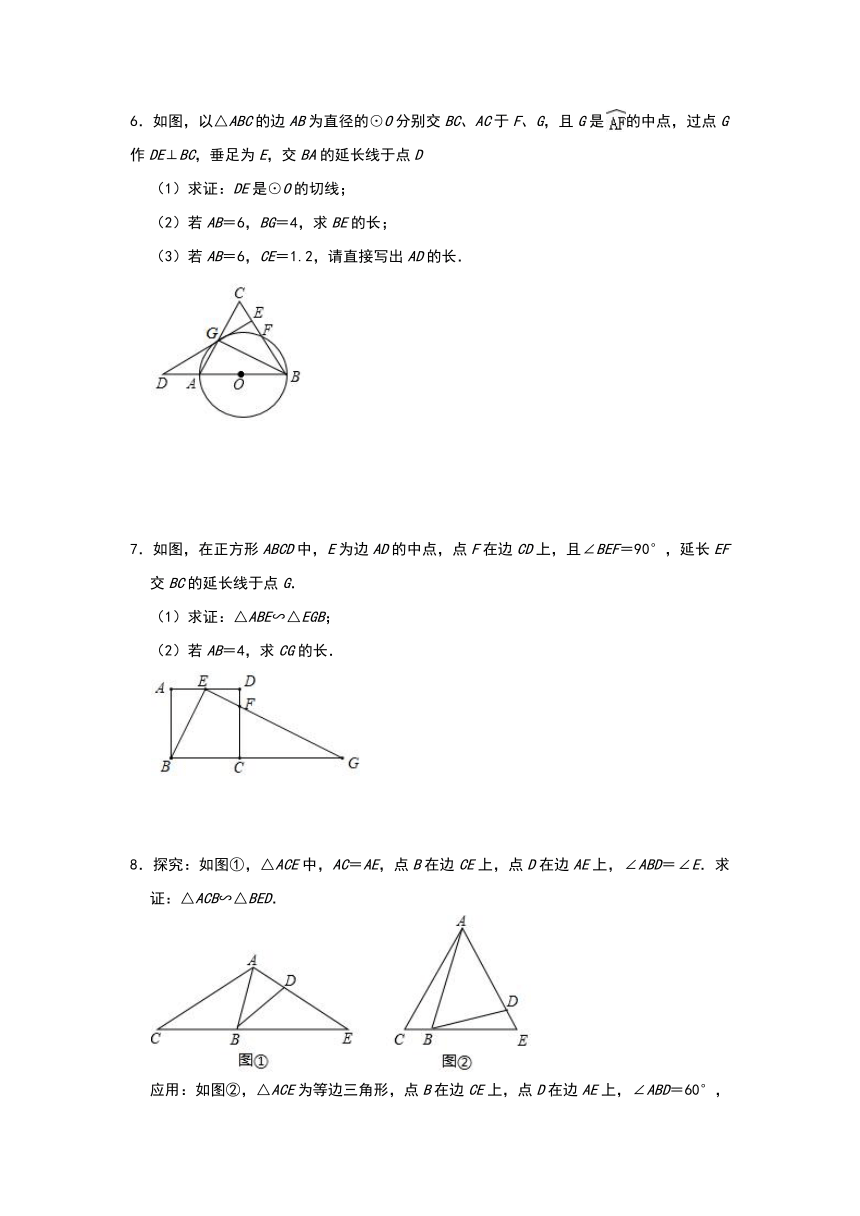
4.如图,已知△ABC中,AT为∠BAC的平分线,
(1)若AB=3,AC=4,BC=5,求△ABT与△ACT的面积之比.
(2)求证:.
5.如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F.
(1)求证:△PFA∽△ABE;
(2)当点P在射线AD上运动时,设PA=x,是否存在实数x,使以P,F,E为顶点的三角形也与△ABE相似?若存在,请求出x的值;若不存在,说明理由.
6.如图,以△ABC的边AB为直径的⊙O分别交BC、AC于F、G,且G是的中点,过点G作DE⊥BC,垂足为E,交BA的延长线于点D
(1)求证:DE是⊙O的切线;
(2)若AB=6,BG=4,求BE的长;
(3)若AB=6,CE=1.2,请直接写出AD的长.
7.如图,在正方形ABCD中,E为边AD的中点,点F在边CD上,且∠BEF=90°,延长EF交BC的延长线于点G.
(1)求证:△ABE∽△EGB;
(2)若AB=4,求CG的长.
8.探究:如图①,△ACE中,AC=AE,点B在边CE上,点D在边AE上,∠ABD=∠E.求证:△ACB∽△BED.
应用:如图②,△ACE为等边三角形,点B在边CE上,点D在边AE上,∠ABD=60°,BC=BE,则△ABD与△BDE的面积比为
.
9.如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s的速度向点C移动,同时动点Q从C出发以1cm/s的速度向点A移动,设它们的运动时间为t.
(1)t为何值时,△CPQ的面积等于△ABC面积的?
(2)运动几秒时,△CPQ与△CBA相似?
(3)在运动过程中,PQ的长度能否为1cm?试说明理由.
10.如图,在正方形ABCD中,E为边AD上的点,点F在边CD上,且CF=3FD,∠BEF=90°
(1)求证:△ABE∽△DEF;
(2)若AB=4,延长EF交BC的延长线于点G,求BG的长
参考答案
1.解:(1).
证明:如图1,过点P作PE⊥AB于点E,PF⊥BC
于点F,
∵∠ABC=90°,
∴PE∥BC,PF∥AB,
∴四边形PEBF是矩形,
∴∠EPF=90°,
∵P是AC的中点,
∴E,F分别是线段AB,BC的中点,
∴PE=BC,PF=AB,
∵∠A=30°,
∴
∵∠MPN=90°,∠EPF=90°,
∴∠MPE=∠NPF,
∴△PEM∽△PNF,
∴,
(2)如图2,过点P作PD⊥AB于点D,PQ⊥BC于点Q,
则四边形PDBQ是矩形,
∴∠PDM=∠PQN=90°,
∵AP=PC,
∴AD=BD=PQ,DP=BQ=QC,
∵∠DPQ=∠MPN=90°,
∴∠DPM=∠QPN,
∴△MDP∽△NQP,
∴,
∵=,
∴.
故答案为:.
2.(1)证明:∵DE∥BC,
∴=,
∵=,
∴=,
∴DF∥BE;
(2)解:∵AF=2,EF=4,
∴AE=AF+EF=6,==,
∴=,
∴AD=AB=2,BD=2AD=4,
∴==,
∵==,
∴=,
又∵∠A=∠A,
∴△ADE∽△AEB,
∴==.
3.解:(1)证明:∵BD、CE是△ABC的高,
∴∠ADB=∠AEC=90°,
∵∠A=∠A,
∴△ACE∽△ABD;
(2)在Rt△ABD中,BD=8,AD=6,
根据勾股定理,得
AB==10,
∵△ACE∽△ABD,
∴=,
∵∠A=∠A,
∴△AED∽△ACB,
∴=,
∵DE=5,
∴BC==.
4.解:(1)过T作TD⊥AB,TE⊥AC,垂足分别为D,E,
∵AT为∠BAC的平分线,
∴TD=TE,
∵S△ABT=AB?TD,S△ACT=AC?TE,AB=3,AC=4,
∴S△ABT:S△ACT=AB:AC=3:4;
(2)设△ABC中BC边上的高为h,
则S△ABT=BT?h,S△ACT=TC?h,
∴S△ABT:S△ACT=BT:TC,
由(1)知S△ABT:S△ACT=AB:AC,
∴.
5.(1)证明:∵AD∥BC,
∴∠PAF=∠AEB.
∵∠PFA=∠ABE=90°,
∴△PFA∽△ABE.
(2)若△EFP∽△ABE,则∠PEF=∠EAB.
∴PE∥AB.
∴四边形ABEP为矩形.
∴PA=EB=2,即x=2.
若△PFE∽△ABE,则∠PEF=∠AEB.
∵∠PAF=∠AEB,
∴∠PEF=∠PAF.
∴PE=PA.
∵PF⊥AE,
∴点F为AE的中点.
∵AE=,
∴EF=AE=.
∵,即,
∴PE=5,即x=5.
∴满足条件的x的值为2或5.
6.证明:(1)如图,连接OG,GB,
∵G是弧AF的中点,
∴∠GBF=∠GBA,
∵OB=OG,
∴∠OBG=∠OGB,
∴∠GBF=∠OGB,
∴OG∥BC,
∴∠OGD=∠GEB,
∵DE⊥CB,
∴∠GEB=90°,
∴∠OGD=90°,
即OG⊥DE且G为半径外端,
∴DE为⊙O切线;
(2)∵AB为⊙O直径,
∴∠AGB=90°,
∴∠AGB=∠GEB,且∠GBA=∠GBE,
∴△GBA∽△EBG,
∴,
∴;
(3)AD=2,根据SAS可知△AGB≌△CGB,
则BC=AB=6,
∴BE=4.8,
∵OG∥BE,
∴,即,
解得:AD=2.
7.(1)证明:∵四边形ABCD为正方形,且∠BEG=90°,
∴∠A=∠BEG,
∵∠ABE+∠EBG=90°,∠G+∠EBG=90°,
∴∠ABE=∠G,
∴△ABE∽△EGB;
(2)∵AB=AD=4,E为AD的中点,
∴AE=DE=2,
在Rt△ABE中,BE===2,
由(1)知,△ABE∽△EGB,
∴=,即:=,
∴BG=10,
∴CG=BG﹣BC=10﹣4=6.
8.证明:(1)∵AC=AE,
∴∠C=∠E,
∵∠ABD=∠E,
∴∠ABD=∠C,
∵∠C+∠CBA+∠CAB=180°,∠CBA+∠ABD+∠DBE=180°,
∴∠BAC=∠DBE,
∴△ACB∽△BED;
(2)∵△ACE是等边三角形,
∴∠E=∠C=60°,
∴∠CAB+∠ABC=120°
∵∠ADB=60°,
∴∠ABC+∠DBE=120°,
∴∠DBE=∠CAB,
又∵∠E=∠C=60°,
∴△ABC∽△DBE,
∵BC=BE,
∴,
∴,
∴,
∴,
∴△ABD与△BDE的面积比为:13:3;
故答案为:13:3.
9.解:(1)经过t秒后,PC=4﹣2t,CQ=t,
当△CPQ的面积等于△ABC面积的时,
即(4﹣2t)?t=××3×4,
解得;t=或t=;
∴经过或秒后,△CPQ的面积等于△ABC面积的;
(2)设经过t秒后两三角形相似,则可分下列两种情况进行求解,
①若Rt△ABC∽Rt△QPC则=,即=,解之得t=1.2;
②若Rt△ABC∽Rt△PQC则=,=,解之得t=;
由P点在BC边上的运动速度为2cm/s,Q点在AC边上的速度为1cm/s,可求出t的取值范围应该为0<t<2,
验证可知①②两种情况下所求的t均满足条件.所以可知要使△CPQ与△CBA相似,所需要的时间为1.2或秒;
(3)∵∠C=90°,
∴(4﹣2t)2+t2=1,
∵此方程无实数解,
∴在运动过程中,PQ的长度不能为1cm.
10.(1)证明:∵四边形ABCD为正方形,
∴∠A=∠D=90°,AB=BC=CD=AD,AD∥BC,
∵∠BEF=90°,
∴∠AEB+∠DEF=90°,
∵∠ABE+∠AEB=∠DEF+∠EBA=90°,
∴∠ABE=∠DEF,
∴△ABE∽△DEF;
(2)解:∵AB=BC=CD=AD=4,CF=3FD,
∴DF=1,CF=3,
∵△ABE∽△DEF,
∴=,即=,
解得:DE=2,
∵AD∥BC,
∴△EDF∽△GCF,
∴=,即=,
∴CG=6,
∴BG=BC+CG=4+6=10.
第27章:相似
精选提升练习(一)
1.在Rt△ABC中,∠ABC=90°,P是线段AC的中点.
(1)如图①,当∠A=30°,且点M,N分别在线段AB,BC上时,∠MPN=90°,写出线段PM与PN的比值,并给予证明;
(2)如图②,当∠A=30°,且点M,N分别在线段AB,BC的延长线上时,∠MPN=90°,线段PM与PN的比值等于
.
2.如图,在△ABC中,点D在边AB上,点E、点F在边AC上,且DE∥BC,=.
(1)求证:DF∥BE;
(2)如果AF=2,EF=4,AB=6,求的值.
3.如图,BD、CE是△ABC的高.
(1)求证:△ACE∽△ABD;
(2)若BD=8,AD=6,DE=5,求BC的长.
4.如图,已知△ABC中,AT为∠BAC的平分线,
(1)若AB=3,AC=4,BC=5,求△ABT与△ACT的面积之比.
(2)求证:.
5.如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F.
(1)求证:△PFA∽△ABE;
(2)当点P在射线AD上运动时,设PA=x,是否存在实数x,使以P,F,E为顶点的三角形也与△ABE相似?若存在,请求出x的值;若不存在,说明理由.
6.如图,以△ABC的边AB为直径的⊙O分别交BC、AC于F、G,且G是的中点,过点G作DE⊥BC,垂足为E,交BA的延长线于点D
(1)求证:DE是⊙O的切线;
(2)若AB=6,BG=4,求BE的长;
(3)若AB=6,CE=1.2,请直接写出AD的长.
7.如图,在正方形ABCD中,E为边AD的中点,点F在边CD上,且∠BEF=90°,延长EF交BC的延长线于点G.
(1)求证:△ABE∽△EGB;
(2)若AB=4,求CG的长.
8.探究:如图①,△ACE中,AC=AE,点B在边CE上,点D在边AE上,∠ABD=∠E.求证:△ACB∽△BED.
应用:如图②,△ACE为等边三角形,点B在边CE上,点D在边AE上,∠ABD=60°,BC=BE,则△ABD与△BDE的面积比为
.
9.如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s的速度向点C移动,同时动点Q从C出发以1cm/s的速度向点A移动,设它们的运动时间为t.
(1)t为何值时,△CPQ的面积等于△ABC面积的?
(2)运动几秒时,△CPQ与△CBA相似?
(3)在运动过程中,PQ的长度能否为1cm?试说明理由.
10.如图,在正方形ABCD中,E为边AD上的点,点F在边CD上,且CF=3FD,∠BEF=90°
(1)求证:△ABE∽△DEF;
(2)若AB=4,延长EF交BC的延长线于点G,求BG的长
参考答案
1.解:(1).
证明:如图1,过点P作PE⊥AB于点E,PF⊥BC
于点F,
∵∠ABC=90°,
∴PE∥BC,PF∥AB,
∴四边形PEBF是矩形,
∴∠EPF=90°,
∵P是AC的中点,
∴E,F分别是线段AB,BC的中点,
∴PE=BC,PF=AB,
∵∠A=30°,
∴
∵∠MPN=90°,∠EPF=90°,
∴∠MPE=∠NPF,
∴△PEM∽△PNF,
∴,
(2)如图2,过点P作PD⊥AB于点D,PQ⊥BC于点Q,
则四边形PDBQ是矩形,
∴∠PDM=∠PQN=90°,
∵AP=PC,
∴AD=BD=PQ,DP=BQ=QC,
∵∠DPQ=∠MPN=90°,
∴∠DPM=∠QPN,
∴△MDP∽△NQP,
∴,
∵=,
∴.
故答案为:.
2.(1)证明:∵DE∥BC,
∴=,
∵=,
∴=,
∴DF∥BE;
(2)解:∵AF=2,EF=4,
∴AE=AF+EF=6,==,
∴=,
∴AD=AB=2,BD=2AD=4,
∴==,
∵==,
∴=,
又∵∠A=∠A,
∴△ADE∽△AEB,
∴==.
3.解:(1)证明:∵BD、CE是△ABC的高,
∴∠ADB=∠AEC=90°,
∵∠A=∠A,
∴△ACE∽△ABD;
(2)在Rt△ABD中,BD=8,AD=6,
根据勾股定理,得
AB==10,
∵△ACE∽△ABD,
∴=,
∵∠A=∠A,
∴△AED∽△ACB,
∴=,
∵DE=5,
∴BC==.
4.解:(1)过T作TD⊥AB,TE⊥AC,垂足分别为D,E,
∵AT为∠BAC的平分线,
∴TD=TE,
∵S△ABT=AB?TD,S△ACT=AC?TE,AB=3,AC=4,
∴S△ABT:S△ACT=AB:AC=3:4;
(2)设△ABC中BC边上的高为h,
则S△ABT=BT?h,S△ACT=TC?h,
∴S△ABT:S△ACT=BT:TC,
由(1)知S△ABT:S△ACT=AB:AC,
∴.
5.(1)证明:∵AD∥BC,
∴∠PAF=∠AEB.
∵∠PFA=∠ABE=90°,
∴△PFA∽△ABE.
(2)若△EFP∽△ABE,则∠PEF=∠EAB.
∴PE∥AB.
∴四边形ABEP为矩形.
∴PA=EB=2,即x=2.
若△PFE∽△ABE,则∠PEF=∠AEB.
∵∠PAF=∠AEB,
∴∠PEF=∠PAF.
∴PE=PA.
∵PF⊥AE,
∴点F为AE的中点.
∵AE=,
∴EF=AE=.
∵,即,
∴PE=5,即x=5.
∴满足条件的x的值为2或5.
6.证明:(1)如图,连接OG,GB,
∵G是弧AF的中点,
∴∠GBF=∠GBA,
∵OB=OG,
∴∠OBG=∠OGB,
∴∠GBF=∠OGB,
∴OG∥BC,
∴∠OGD=∠GEB,
∵DE⊥CB,
∴∠GEB=90°,
∴∠OGD=90°,
即OG⊥DE且G为半径外端,
∴DE为⊙O切线;
(2)∵AB为⊙O直径,
∴∠AGB=90°,
∴∠AGB=∠GEB,且∠GBA=∠GBE,
∴△GBA∽△EBG,
∴,
∴;
(3)AD=2,根据SAS可知△AGB≌△CGB,
则BC=AB=6,
∴BE=4.8,
∵OG∥BE,
∴,即,
解得:AD=2.
7.(1)证明:∵四边形ABCD为正方形,且∠BEG=90°,
∴∠A=∠BEG,
∵∠ABE+∠EBG=90°,∠G+∠EBG=90°,
∴∠ABE=∠G,
∴△ABE∽△EGB;
(2)∵AB=AD=4,E为AD的中点,
∴AE=DE=2,
在Rt△ABE中,BE===2,
由(1)知,△ABE∽△EGB,
∴=,即:=,
∴BG=10,
∴CG=BG﹣BC=10﹣4=6.
8.证明:(1)∵AC=AE,
∴∠C=∠E,
∵∠ABD=∠E,
∴∠ABD=∠C,
∵∠C+∠CBA+∠CAB=180°,∠CBA+∠ABD+∠DBE=180°,
∴∠BAC=∠DBE,
∴△ACB∽△BED;
(2)∵△ACE是等边三角形,
∴∠E=∠C=60°,
∴∠CAB+∠ABC=120°
∵∠ADB=60°,
∴∠ABC+∠DBE=120°,
∴∠DBE=∠CAB,
又∵∠E=∠C=60°,
∴△ABC∽△DBE,
∵BC=BE,
∴,
∴,
∴,
∴,
∴△ABD与△BDE的面积比为:13:3;
故答案为:13:3.
9.解:(1)经过t秒后,PC=4﹣2t,CQ=t,
当△CPQ的面积等于△ABC面积的时,
即(4﹣2t)?t=××3×4,
解得;t=或t=;
∴经过或秒后,△CPQ的面积等于△ABC面积的;
(2)设经过t秒后两三角形相似,则可分下列两种情况进行求解,
①若Rt△ABC∽Rt△QPC则=,即=,解之得t=1.2;
②若Rt△ABC∽Rt△PQC则=,=,解之得t=;
由P点在BC边上的运动速度为2cm/s,Q点在AC边上的速度为1cm/s,可求出t的取值范围应该为0<t<2,
验证可知①②两种情况下所求的t均满足条件.所以可知要使△CPQ与△CBA相似,所需要的时间为1.2或秒;
(3)∵∠C=90°,
∴(4﹣2t)2+t2=1,
∵此方程无实数解,
∴在运动过程中,PQ的长度不能为1cm.
10.(1)证明:∵四边形ABCD为正方形,
∴∠A=∠D=90°,AB=BC=CD=AD,AD∥BC,
∵∠BEF=90°,
∴∠AEB+∠DEF=90°,
∵∠ABE+∠AEB=∠DEF+∠EBA=90°,
∴∠ABE=∠DEF,
∴△ABE∽△DEF;
(2)解:∵AB=BC=CD=AD=4,CF=3FD,
∴DF=1,CF=3,
∵△ABE∽△DEF,
∴=,即=,
解得:DE=2,
∵AD∥BC,
∴△EDF∽△GCF,
∴=,即=,
∴CG=6,
∴BG=BC+CG=4+6=10.
