2020-2021学年九年级数学人教版下册第27章 《相似 》章节培优训练(四)(Word版 含答案)
文档属性
| 名称 | 2020-2021学年九年级数学人教版下册第27章 《相似 》章节培优训练(四)(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 175.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 11:05:32 | ||
图片预览



文档简介
九年级下册第27章
《相似
》
章节培优训练(四)
1.如图所示,在等腰△ABC中,AB=AC=5cm,BC=8cm,点P由点A出发沿AB方向向点B匀速运动,同时点Q由点B出发沿BC方向向点C匀速运动,它们的速度均为1cm/s.连接PQ,设运动时间为t(s)(0<t<5),解答下列问题:
(1)当t为何值时,△BPQ的面积为cm2;
(2)在点P,Q的运动中,是否存在时间t,使△BPQ为等腰三角形.若存在,请求出对应的时间t;若不存在,请说明理由.
2.已知:如图,AD∥BC,∠ABD=∠C,AE⊥BD,DF⊥BC,点E、F分别为垂足.
(1)求证:=;
(2)联结EF,如果∠ADB=∠BDF,求证:DF?DC=EF?BC.
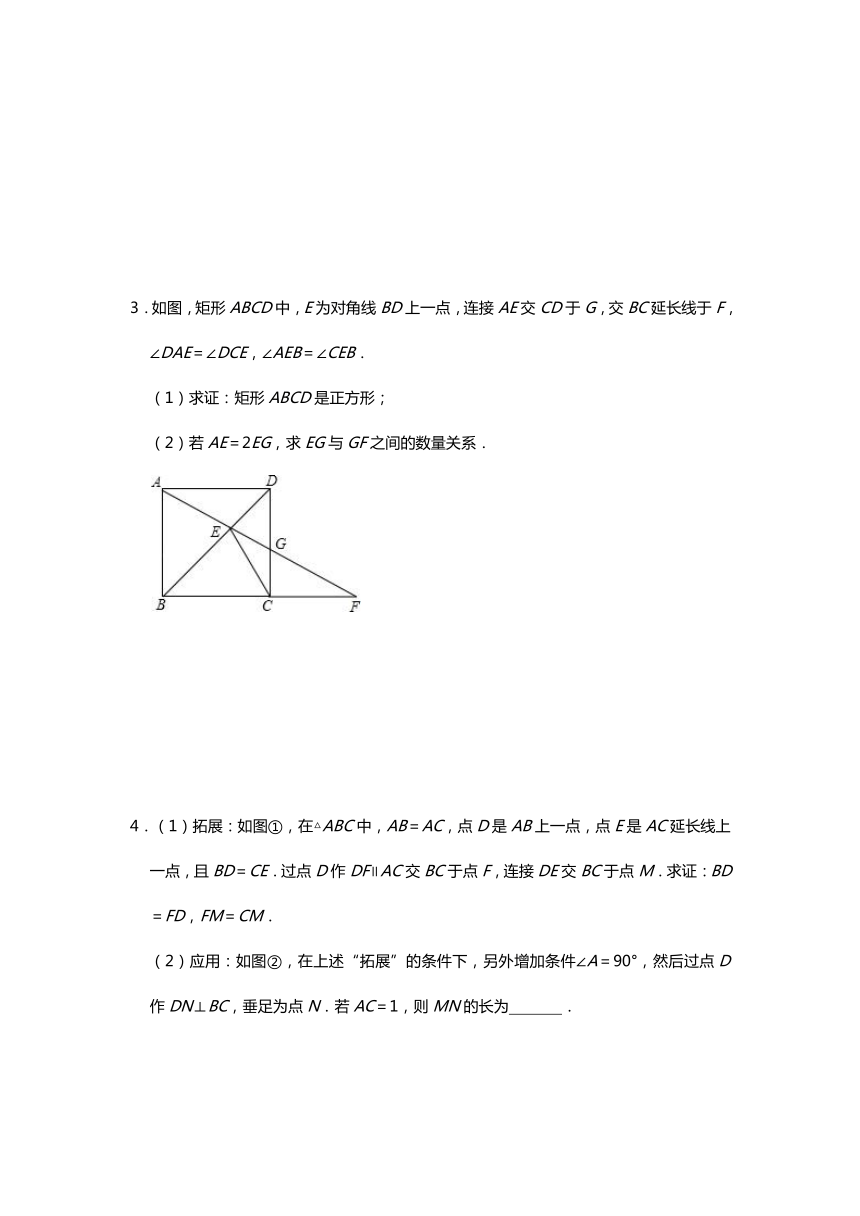
3.如图,矩形ABCD中,E为对角线BD上一点,连接AE交CD于G,交BC延长线于F,∠DAE=∠DCE,∠AEB=∠CEB.
(1)求证:矩形ABCD是正方形;
(2)若AE=2EG,求EG与GF之间的数量关系.
4.(1)拓展:如图①,在△ABC中,AB=AC,点D是AB上一点,点E是AC延长线上一点,且BD=CE.过点D作DF∥AC交BC于点F,连接DE交BC于点M.求证:BD=FD,FM=CM.
(2)应用:如图②,在上述“拓展”的条件下,另外增加条件∠A=90°,然后过点D作DN⊥BC,垂足为点N.若AC=1,则MN的长为
.
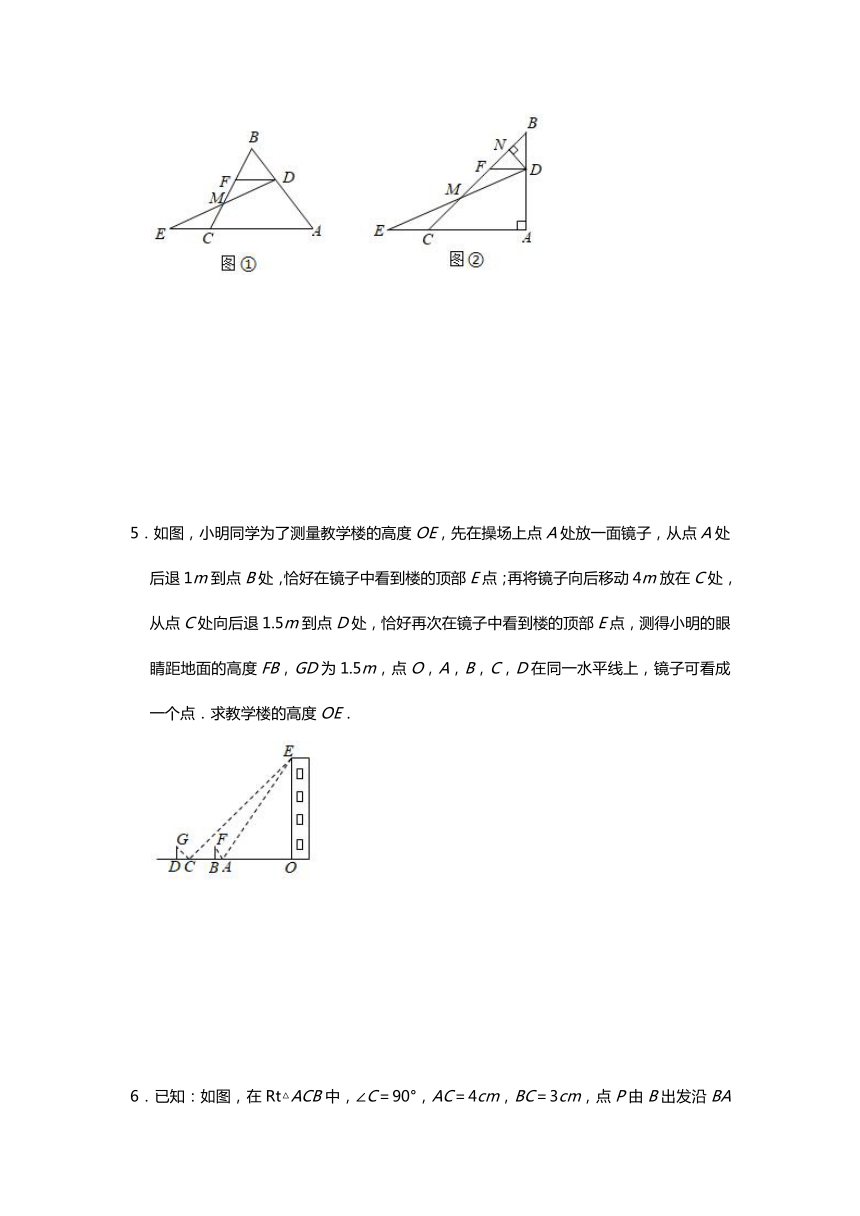
5.如图,小明同学为了测量教学楼的高度OE,先在操场上点A处放一面镜子,从点A处后退1m到点B处,恰好在镜子中看到楼的顶部E点;再将镜子向后移动4m放在C处,从点C处向后退1.5m到点D处,恰好再次在镜子中看到楼的顶部E点,测得小明的眼睛距地面的高度FB,GD为1.5m,点O,A,B,C,D在同一水平线上,镜子可看成一个点.求教学楼的高度OE.
6.已知:如图,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2),当t为何值时,以A、P、Q为顶点的三角形与△ABC相似?
7.如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,交AB的延长线于点E,AC平分∠DAB.且OA=3,AC=.
(1)求证:AD⊥DE;
(2)若点P为线段CE上一动点,当△PBE与△ACE相似时,求EP的长.
8.如图,在△ABC中,AB=AC,△ADE∽△ABC,连接BD,CE.
(1)判断BD与CE的数量关系,并证明你的结论;
(2)若AB=3,AD=3,∠BAC=105°,∠CAD=30°.
①BD的长为
;
②点P,Q分别为BC,DE的中点,连接PQ,写出求PQ长的思路.
9.新型冠状病毒感染引发“疫情就是命令,现场就是战场”.家住武汉火神山医院旁的小华,目睹这与时间赛跑的建设场面,在家里的小华从离窗台A水平距离2m的M点望去,通过窗台A处刚好俯瞰到远处医院箱式板房顶部远端E点,小华又向窗户方向前进0.8m到Q点,恰好通过窗台A处看到板房顶部近处D点,已知AB、CD、EF、MN都垂直于地面BC,N、F在直线BC上,MQ、DE都平行于地面BC,BC长300m,请你帮助小华计算DE的长度.
10.如图,平面直角坐标系中三点A(3,0),B(0,2),P(x,0)(x<0),连结BP,过点P作PC⊥PB交过点A的直线x=3于点C(3,y)
(1)试把y用含x的代数式来表示;
(2)当x=﹣1时,求BC与PA的交点Q的坐标.
参考答案
1.解:(1)如图,过点A作AE⊥BC于E,过点P作PF⊥BC于F,
∵AB=AC=5cm,BC=8cm,AE⊥BC,
∴BE=EC=4cm,
∴AE===3cm,
∵∠PFB=∠AEB=90°,∠B=∠B,
∴△AEB∽△PFB,
∴=,
∴=,
∴PF=cm,BF=cm,
∵△BPQ的面积为cm2,
∴×BQ×PF=,
∴×t×=,
∴t1=1,t2=4,
∴当t为1或4时,△BPQ的面积为cm2;
(2)当BP=BQ时,则5﹣t=t,
∴t=,
当BQ=PQ时,∵PQ2=PF2+QF2,
∴t2=[]2+[﹣t]2,
∴t1=5(不合题意),t2=,
当BP=PQ时,则点P在BF的垂直平分线上,
∴=,
∴t=,
综上所述:t的值为或或时,△BPQ为等腰三角形.
2.(1)证明:∵AE⊥BD,DF⊥BC,
∴∠AEB=∠DFC=90°,
∵∠ABD=∠C,
∴△ABE∽△DCF,
∴,
∵AD∥BC,
∴∠ADB=∠DBC,
∴△ABD∽△DCB,
∴,
∴;
(2)证明:∵∠ADB=∠DBF,∠ADB=∠BDF,∠BFD=90°,
∴∠DBF=∠BDF,
∴∠DBF=ADE=45°,
∴△AED和△BFD都是等腰直角三角形,
∴,
又∵∠ADE=∠BDF,
∴△ADB∽△EDF,
∴∠ABD=∠EFD,
∵∠ABD=∠C,
∴∠EFD=∠C,
∵∠EDF=∠DBC,
∴△EDF∽△DBC,
∴,
∴DF?DC=EF?BC.
3.证明:(1)∵∠AEB=∠CEB,∠ADE=∠CDE,
∴∠DAE=∠DCE,
在△ADE和△CDE中,,
∴△ADE≌△CDE(AAS),
∴AD=CD,
∴矩形ABCD是正方形;
(2)GF=3EG;
∵△ADE≌△CDE,
∴AE=CE,
∵四边形ABCD是矩形,
∴AD∥BF,∴∠DAE=∠F,
∵∠DAE=∠DCE,
∴∠DCE=∠F,
又∵∠GEC=∠CEF,
∴△ECG∽△EFC,
∴,
∵AE=2EG,
∴CE=2EG,
∴,
∴EF=4EG,
∴GF=3EG.
4.(1)证明:方法一:
∵AB=AC,
∴∠B=∠BCA,
∵DF∥AC,
∴∠BFD=∠BCA,∠FDM=∠CEM,
∴∠B=∠BFD,
∴BD=FD,
方法二:
∵DF∥AC,
∴△BFD∽△BCA,
∵AB=AC,
∴BD=FD;
∵BD=CE,
∴DF=CE,
在△FDM和△CEM中,
,
∴△FDM≌△CEM(AAS),
∴FM=CM;
(2)解:∵BD=DF,DN⊥BC,
∴BN=FN,
∵FM=CM,
∴BC=BF+CF=2FN+2FM=2MN,
∵AB=AC=1,
∴BC===,
∴MN=BC=.
故答案为:.
5.解:由已知得,AB=1m,CD=1.5m,AC=4m,FB=GD=1.5m,∠AOE=∠ABF=∠CDG=90°,∠BAF=∠OAE,∠DCG=∠OCE.
∵∠BAF=∠OAE,∠ABF=∠AOE,
∴△BAF∽△OAE,
∴=,即=,
∴OE=1.5OA,
∵∠DCG=∠OCE,∠CDG=∠COE,
∴△GDC∽△EOC,
∴=,即=,
∴OE=OA+4,
∴OE=1.5OA,
∴1.5OA=OA+4,
∴OA=8m,OE=12m.
答:教学楼的高度OE为12m.
6.解:∵∠C=90°,AC=4cm,BC=3cm,
∴AB==5,
则BP=t,AQ=2t,AP=5﹣t,
∵∠PAQ=∠BAC,
当=时,△APQ∽△ABC,即=,解得t=;
当=时,△APQ∽△ACB,即=,解得t=;
答:t为s或s时,以A、P、Q为顶点的三角形与△ABC相似.
7.(1)证明:连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
又∵AC平分∠DAB,
∴∠DAC=∠OAC,
∴∠DAC=∠OCA,
∴OC∥AD,
又∵DE是⊙O的切线,
∴OC⊥DE,
∴AD⊥DE;
(2)解:连接BC,
∵AB为⊙O直径,
∴∠ACB=90°,
又∵AB=2OA=6,AC=,
∴cos∠BAC=,
∴∠BAC=30°,BC=3,
∴△BCO为等边三角形,
∴∠ECB=30°,∠BEC=30°,
∴EC=AC=,BE=BC=BO=AO=3,
①当BP∥AC时,△BPE∽△ACE,
∴,
即,
∴PE=;
②当点P与点C重合时,△PBE∽△ACE,
∴PE=CE=;
综上:当△PBE与△ACE相似时,EP=或.
8.解:(1)结论:BD=CE,
理由:∵△ADE∽△ABC,
∴∠BAC=∠DAE,
∴∠BAC+∠CAD=∠CAD+∠DAE,
即∠BAD=∠CAE,
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE;
(2)①如图1中,作DH⊥BA交BA的延长线于H.
∵∠BAD=∠BAC+∠DAC=135°,
∴∠DAH=45°,
∵∠H=90°,AD=3,
∴AH=DH=3,
在Rt△BDH中,BD===3,
故答案为:3;
(2)如图2中,连接PQ,AQ,AP,作QH⊥PA交PA的延长线于H.
在Rt△ABP中,AP=AB?sin37.5°,
在Rt△AQD中,AQ=AD?sin37.5°,
在Rt△AHQ中,根据∠HAQ=45°,可得AH=HQ=AQ,
求出HQ,PH,根据PQ=计算即可.
9.解:延长ED交AB于H,延长MQ交BA的延长线于T.
由题意MT=2m,MQ=0.8m,
∴QT=MT﹣MQ=2﹣0.8=1.2(m),
∵四边形BCDH是矩形,
∴DH=BC=300(m),
∵QT∥DH,
∴===,
∵MT∥DE,
∴=,
∴=,
∴EH=500(m),
∴DE=500﹣300=200(m)
10.解:(1)∵PC⊥PB,BO⊥PO
∴∠CPA+∠OPB=90°,∠PBO+∠OPB=90°
∴∠CPA=∠PBO
∵A(2,0),C(2,y)在直线x=3上
∴∠BOP=∠PAC=90°
∴△BOP∽△PAC
∴=,
∴=,
∵x<0,y<0,
∴=
∴y=﹣x2+x.
(2)当x=﹣1时,y=﹣2,
∴C点的坐标为(3,﹣2);
设直线BC的解析式为y=kx+2,将C点坐标代入后可得:
3k+2=﹣2,k=﹣,
因此直线BC的解析式为y=﹣x+2.
当y=0时,0=﹣x+2,x=.
因此Q点的坐标为(,0).
《相似
》
章节培优训练(四)
1.如图所示,在等腰△ABC中,AB=AC=5cm,BC=8cm,点P由点A出发沿AB方向向点B匀速运动,同时点Q由点B出发沿BC方向向点C匀速运动,它们的速度均为1cm/s.连接PQ,设运动时间为t(s)(0<t<5),解答下列问题:
(1)当t为何值时,△BPQ的面积为cm2;
(2)在点P,Q的运动中,是否存在时间t,使△BPQ为等腰三角形.若存在,请求出对应的时间t;若不存在,请说明理由.
2.已知:如图,AD∥BC,∠ABD=∠C,AE⊥BD,DF⊥BC,点E、F分别为垂足.
(1)求证:=;
(2)联结EF,如果∠ADB=∠BDF,求证:DF?DC=EF?BC.
3.如图,矩形ABCD中,E为对角线BD上一点,连接AE交CD于G,交BC延长线于F,∠DAE=∠DCE,∠AEB=∠CEB.
(1)求证:矩形ABCD是正方形;
(2)若AE=2EG,求EG与GF之间的数量关系.
4.(1)拓展:如图①,在△ABC中,AB=AC,点D是AB上一点,点E是AC延长线上一点,且BD=CE.过点D作DF∥AC交BC于点F,连接DE交BC于点M.求证:BD=FD,FM=CM.
(2)应用:如图②,在上述“拓展”的条件下,另外增加条件∠A=90°,然后过点D作DN⊥BC,垂足为点N.若AC=1,则MN的长为
.
5.如图,小明同学为了测量教学楼的高度OE,先在操场上点A处放一面镜子,从点A处后退1m到点B处,恰好在镜子中看到楼的顶部E点;再将镜子向后移动4m放在C处,从点C处向后退1.5m到点D处,恰好再次在镜子中看到楼的顶部E点,测得小明的眼睛距地面的高度FB,GD为1.5m,点O,A,B,C,D在同一水平线上,镜子可看成一个点.求教学楼的高度OE.
6.已知:如图,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2),当t为何值时,以A、P、Q为顶点的三角形与△ABC相似?
7.如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,交AB的延长线于点E,AC平分∠DAB.且OA=3,AC=.
(1)求证:AD⊥DE;
(2)若点P为线段CE上一动点,当△PBE与△ACE相似时,求EP的长.
8.如图,在△ABC中,AB=AC,△ADE∽△ABC,连接BD,CE.
(1)判断BD与CE的数量关系,并证明你的结论;
(2)若AB=3,AD=3,∠BAC=105°,∠CAD=30°.
①BD的长为
;
②点P,Q分别为BC,DE的中点,连接PQ,写出求PQ长的思路.
9.新型冠状病毒感染引发“疫情就是命令,现场就是战场”.家住武汉火神山医院旁的小华,目睹这与时间赛跑的建设场面,在家里的小华从离窗台A水平距离2m的M点望去,通过窗台A处刚好俯瞰到远处医院箱式板房顶部远端E点,小华又向窗户方向前进0.8m到Q点,恰好通过窗台A处看到板房顶部近处D点,已知AB、CD、EF、MN都垂直于地面BC,N、F在直线BC上,MQ、DE都平行于地面BC,BC长300m,请你帮助小华计算DE的长度.
10.如图,平面直角坐标系中三点A(3,0),B(0,2),P(x,0)(x<0),连结BP,过点P作PC⊥PB交过点A的直线x=3于点C(3,y)
(1)试把y用含x的代数式来表示;
(2)当x=﹣1时,求BC与PA的交点Q的坐标.
参考答案
1.解:(1)如图,过点A作AE⊥BC于E,过点P作PF⊥BC于F,
∵AB=AC=5cm,BC=8cm,AE⊥BC,
∴BE=EC=4cm,
∴AE===3cm,
∵∠PFB=∠AEB=90°,∠B=∠B,
∴△AEB∽△PFB,
∴=,
∴=,
∴PF=cm,BF=cm,
∵△BPQ的面积为cm2,
∴×BQ×PF=,
∴×t×=,
∴t1=1,t2=4,
∴当t为1或4时,△BPQ的面积为cm2;
(2)当BP=BQ时,则5﹣t=t,
∴t=,
当BQ=PQ时,∵PQ2=PF2+QF2,
∴t2=[]2+[﹣t]2,
∴t1=5(不合题意),t2=,
当BP=PQ时,则点P在BF的垂直平分线上,
∴=,
∴t=,
综上所述:t的值为或或时,△BPQ为等腰三角形.
2.(1)证明:∵AE⊥BD,DF⊥BC,
∴∠AEB=∠DFC=90°,
∵∠ABD=∠C,
∴△ABE∽△DCF,
∴,
∵AD∥BC,
∴∠ADB=∠DBC,
∴△ABD∽△DCB,
∴,
∴;
(2)证明:∵∠ADB=∠DBF,∠ADB=∠BDF,∠BFD=90°,
∴∠DBF=∠BDF,
∴∠DBF=ADE=45°,
∴△AED和△BFD都是等腰直角三角形,
∴,
又∵∠ADE=∠BDF,
∴△ADB∽△EDF,
∴∠ABD=∠EFD,
∵∠ABD=∠C,
∴∠EFD=∠C,
∵∠EDF=∠DBC,
∴△EDF∽△DBC,
∴,
∴DF?DC=EF?BC.
3.证明:(1)∵∠AEB=∠CEB,∠ADE=∠CDE,
∴∠DAE=∠DCE,
在△ADE和△CDE中,,
∴△ADE≌△CDE(AAS),
∴AD=CD,
∴矩形ABCD是正方形;
(2)GF=3EG;
∵△ADE≌△CDE,
∴AE=CE,
∵四边形ABCD是矩形,
∴AD∥BF,∴∠DAE=∠F,
∵∠DAE=∠DCE,
∴∠DCE=∠F,
又∵∠GEC=∠CEF,
∴△ECG∽△EFC,
∴,
∵AE=2EG,
∴CE=2EG,
∴,
∴EF=4EG,
∴GF=3EG.
4.(1)证明:方法一:
∵AB=AC,
∴∠B=∠BCA,
∵DF∥AC,
∴∠BFD=∠BCA,∠FDM=∠CEM,
∴∠B=∠BFD,
∴BD=FD,
方法二:
∵DF∥AC,
∴△BFD∽△BCA,
∵AB=AC,
∴BD=FD;
∵BD=CE,
∴DF=CE,
在△FDM和△CEM中,
,
∴△FDM≌△CEM(AAS),
∴FM=CM;
(2)解:∵BD=DF,DN⊥BC,
∴BN=FN,
∵FM=CM,
∴BC=BF+CF=2FN+2FM=2MN,
∵AB=AC=1,
∴BC===,
∴MN=BC=.
故答案为:.
5.解:由已知得,AB=1m,CD=1.5m,AC=4m,FB=GD=1.5m,∠AOE=∠ABF=∠CDG=90°,∠BAF=∠OAE,∠DCG=∠OCE.
∵∠BAF=∠OAE,∠ABF=∠AOE,
∴△BAF∽△OAE,
∴=,即=,
∴OE=1.5OA,
∵∠DCG=∠OCE,∠CDG=∠COE,
∴△GDC∽△EOC,
∴=,即=,
∴OE=OA+4,
∴OE=1.5OA,
∴1.5OA=OA+4,
∴OA=8m,OE=12m.
答:教学楼的高度OE为12m.
6.解:∵∠C=90°,AC=4cm,BC=3cm,
∴AB==5,
则BP=t,AQ=2t,AP=5﹣t,
∵∠PAQ=∠BAC,
当=时,△APQ∽△ABC,即=,解得t=;
当=时,△APQ∽△ACB,即=,解得t=;
答:t为s或s时,以A、P、Q为顶点的三角形与△ABC相似.
7.(1)证明:连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
又∵AC平分∠DAB,
∴∠DAC=∠OAC,
∴∠DAC=∠OCA,
∴OC∥AD,
又∵DE是⊙O的切线,
∴OC⊥DE,
∴AD⊥DE;
(2)解:连接BC,
∵AB为⊙O直径,
∴∠ACB=90°,
又∵AB=2OA=6,AC=,
∴cos∠BAC=,
∴∠BAC=30°,BC=3,
∴△BCO为等边三角形,
∴∠ECB=30°,∠BEC=30°,
∴EC=AC=,BE=BC=BO=AO=3,
①当BP∥AC时,△BPE∽△ACE,
∴,
即,
∴PE=;
②当点P与点C重合时,△PBE∽△ACE,
∴PE=CE=;
综上:当△PBE与△ACE相似时,EP=或.
8.解:(1)结论:BD=CE,
理由:∵△ADE∽△ABC,
∴∠BAC=∠DAE,
∴∠BAC+∠CAD=∠CAD+∠DAE,
即∠BAD=∠CAE,
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE;
(2)①如图1中,作DH⊥BA交BA的延长线于H.
∵∠BAD=∠BAC+∠DAC=135°,
∴∠DAH=45°,
∵∠H=90°,AD=3,
∴AH=DH=3,
在Rt△BDH中,BD===3,
故答案为:3;
(2)如图2中,连接PQ,AQ,AP,作QH⊥PA交PA的延长线于H.
在Rt△ABP中,AP=AB?sin37.5°,
在Rt△AQD中,AQ=AD?sin37.5°,
在Rt△AHQ中,根据∠HAQ=45°,可得AH=HQ=AQ,
求出HQ,PH,根据PQ=计算即可.
9.解:延长ED交AB于H,延长MQ交BA的延长线于T.
由题意MT=2m,MQ=0.8m,
∴QT=MT﹣MQ=2﹣0.8=1.2(m),
∵四边形BCDH是矩形,
∴DH=BC=300(m),
∵QT∥DH,
∴===,
∵MT∥DE,
∴=,
∴=,
∴EH=500(m),
∴DE=500﹣300=200(m)
10.解:(1)∵PC⊥PB,BO⊥PO
∴∠CPA+∠OPB=90°,∠PBO+∠OPB=90°
∴∠CPA=∠PBO
∵A(2,0),C(2,y)在直线x=3上
∴∠BOP=∠PAC=90°
∴△BOP∽△PAC
∴=,
∴=,
∵x<0,y<0,
∴=
∴y=﹣x2+x.
(2)当x=﹣1时,y=﹣2,
∴C点的坐标为(3,﹣2);
设直线BC的解析式为y=kx+2,将C点坐标代入后可得:
3k+2=﹣2,k=﹣,
因此直线BC的解析式为y=﹣x+2.
当y=0时,0=﹣x+2,x=.
因此Q点的坐标为(,0).
