2020-2021学年九年级数学人教版下册第27章 《相似 》章节培优训练(一)(Word版 含答案)
文档属性
| 名称 | 2020-2021学年九年级数学人教版下册第27章 《相似 》章节培优训练(一)(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 134.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 11:07:56 | ||
图片预览


文档简介
九年级下册第27章
《相似
》
章节培优训练(一)
1.已知:如图,D、E分别是△ABC的边AB、AC上的点,且∠AED=∠ABC,联结BE、CD相交于点F.
(1)求证:∠ABE=∠ACD;
(2)如果ED=EC,求证:.
2.如图,在△ABC中,点D在边AB上,点E、点F在边AC上,且DE∥BC,=.
(1)求证:DF∥BE;
(2)如果AF=2,EF=4,AB=6,求的值.
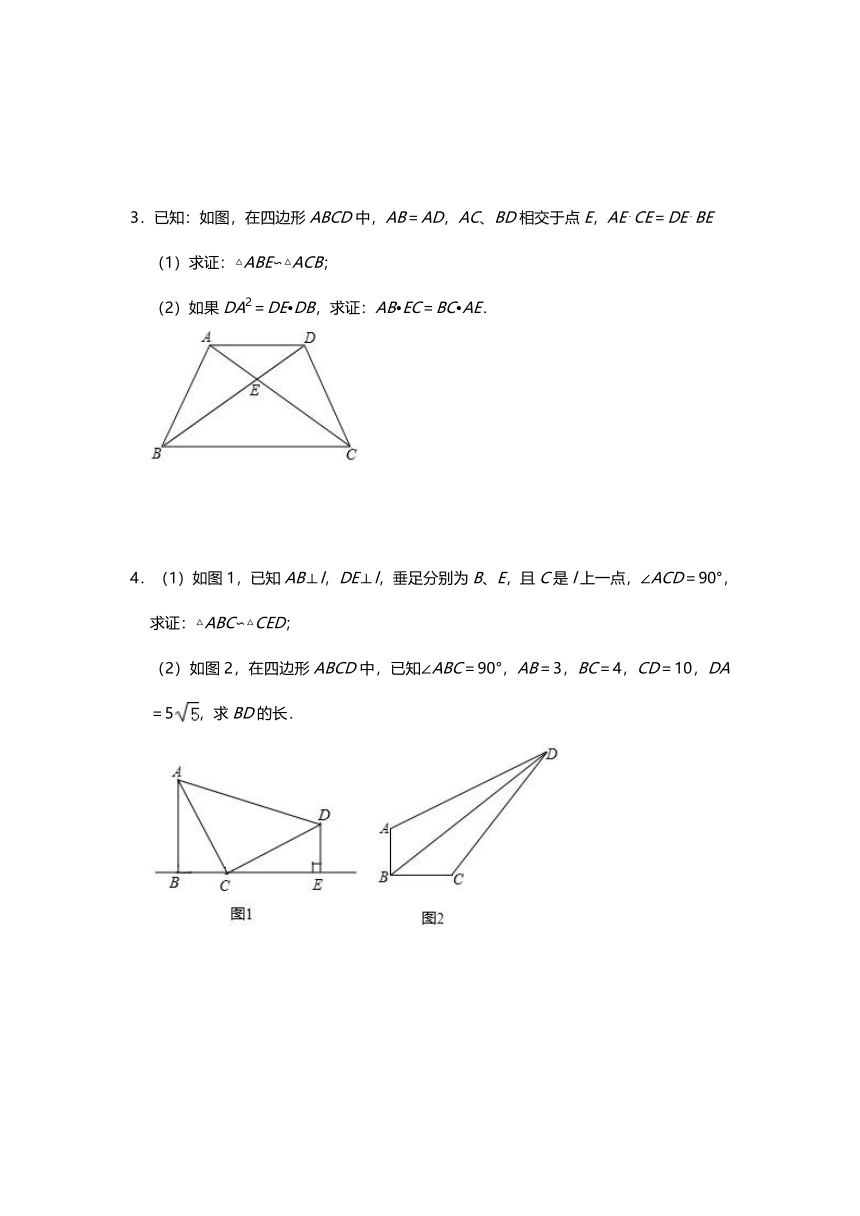
3.已知:如图,在四边形ABCD中,AB=AD,AC、BD相交于点E,AE?CE=DE?BE
(1)求证:△ABE∽△ACB;
(2)如果DA2=DE?DB,求证:AB?EC=BC?AE.
4.(1)如图1,已知AB⊥l,DE⊥l,垂足分别为B、E,且C是l上一点,∠ACD=90°,求证:△ABC∽△CED;
(2)如图2,在四边形ABCD中,已知∠ABC=90°,AB=3,BC=4,CD=10,DA=5,求BD的长.
5.如图,在正方形ABCD中,E是AD的中点,点F在CD上,且CF=3FD.
(1)求证:△ABE∽△DEF;
(2)△ABE与△BEF相似吗?为什么?
6.如图,AB为⊙O的直径,D是弧BC的中点,DE⊥AC交AC的延长线于E,⊙O的切线BF交AD的延长线于F.
(1)求证:DE是⊙O的切线;
(2)若DE=4,⊙O的半径为5.求BF的长.
7.如图,点E是正方形ABCD的对角线AC上的一个动点(不与A、C重合),作EF⊥AC交边BC于点F,连接AF、BE交于点G.
(1)求证:△CAF∽△CBE;
(2)若AF平分∠BAC,求证:AC2=2AG?AF.
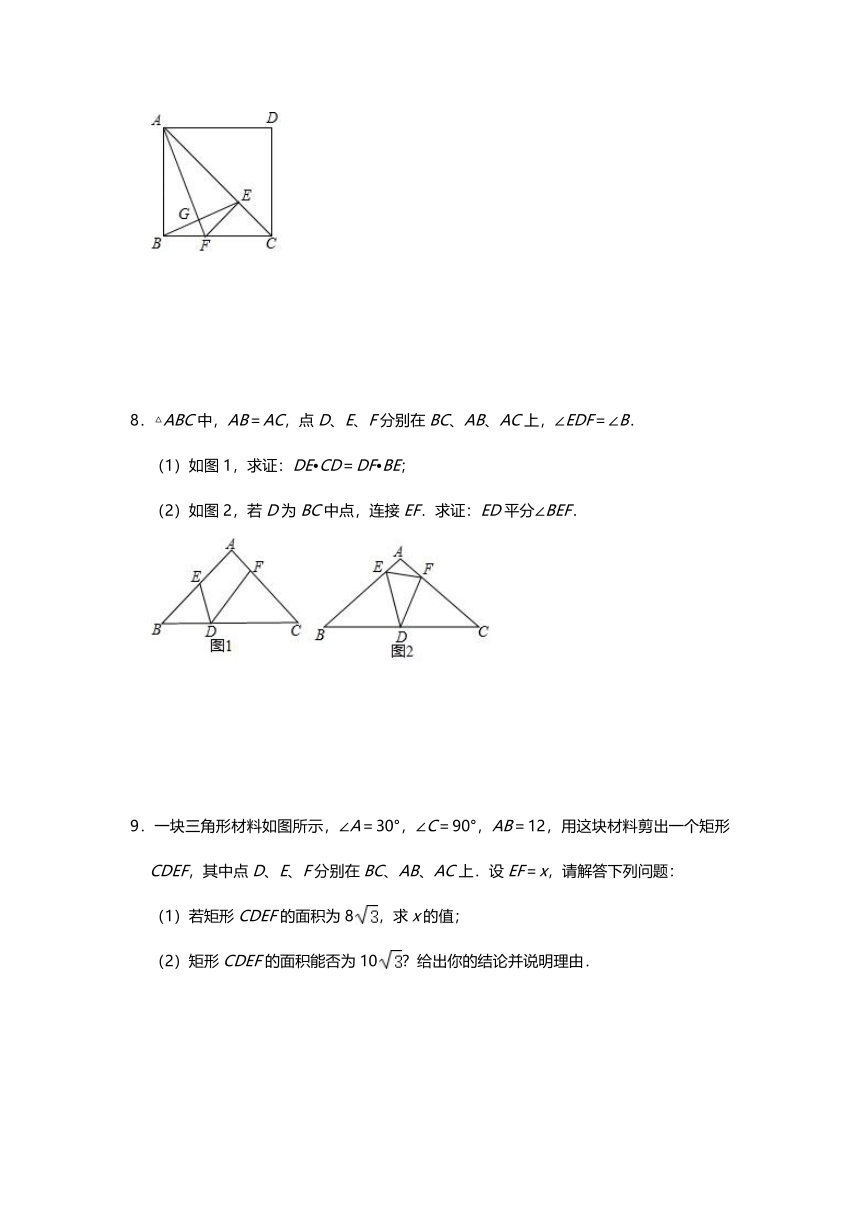
8.△ABC中,AB=AC,点D、E、F分别在BC、AB、AC上,∠EDF=∠B.
(1)如图1,求证:DE?CD=DF?BE;
(2)如图2,若D为BC中点,连接EF.求证:ED平分∠BEF.
9.一块三角形材料如图所示,∠A=30°,∠C=90°,AB=12,用这块材料剪出一个矩形CDEF,其中点D、E、F分别在BC、AB、AC上.设EF=x,请解答下列问题:
(1)若矩形CDEF的面积为8,求x的值;
(2)矩形CDEF的面积能否为10?给出你的结论并说明理由.
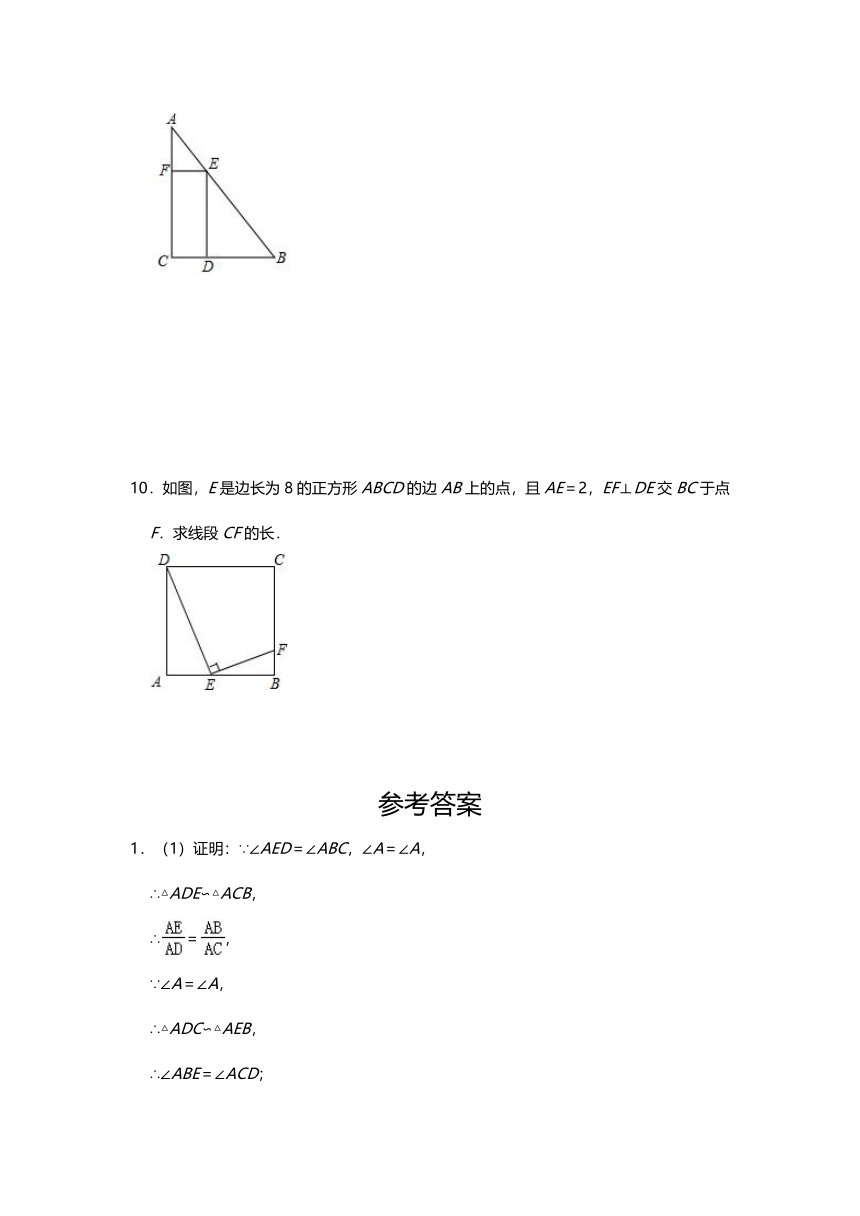
10.如图,E是边长为8的正方形ABCD的边AB上的点,且AE=2,EF⊥DE交BC于点F.求线段CF的长.
参考答案
1.(1)证明:∵∠AED=∠ABC,∠A=∠A,
∴△ADE∽△ACB,
∴=,
∵∠A=∠A,
∴△ADC∽△AEB,
∴∠ABE=∠ACD;
(2)证明:∵ED=EC,
∴∠EDC=∠ECD,
∴∠EDC=∠EBD,
∵∠DEF=∠DEB,
∴△EDF∽△EBD,
∴==,
()2=?,
∴.
2.(1)证明:∵DE∥BC,
∴=,
∵=,
∴=,
∴DF∥BE;
(2)解:∵AF=2,EF=4,
∴AE=AF+EF=6,==,
∴=,
∴AD=AB=2,BD=2AD=4,
∴==,
∵==,
∴=,
又∵∠A=∠A,
∴△ADE∽△AEB,
∴==.
3.证明:(1)∵AE?CE=DE?BE,∠AED=∠BEC,
∴△ADE∽△CBE,
∴∠DAE=∠CBE,∠ADE=∠BCE,
∵AB=AD,
∴∠ADB=∠ABE,
∴∠ABE=∠ACB,
∵∠BAE=∠CAB,
∴△ABE∽△ACB;
(2)∵DA2=DE?DB,∠ADB=∠ADE,
∴△ADB∽△ADE,
∴=,
∵△ABE∽△ACB,
∴=,
∴AD=,
∴==,
∴AB?EC=BC?AE.
4.证明:(1)∵AB⊥l,DE⊥l,
∴∠ABC=∠CED=90°,∠ACB+∠BAC=90°,
∵∠ACD=90°,
∴∠ACB+∠DCE=90°,
∴∠BAC=∠DCE,
∴△ABC∽△CED;
(2)如图,连接AC,
∵∠ABC=90°,
∴AC=,
∵AD=5,CD=10,
∴△ACD满足AC2+CD2=AD2,
∴∠ACD=90°,
如图,过点D作DE⊥BC延长线于点E,
由(1)得此时△ABC∽△CED,
∴,
∴CE=6,DE=8,
在Rt△BDE中,BD=.
5.证明:(1)∵四边形ABCD为正方形,
∴∠A=∠D=90°,AB=AD=CD,
设AB=AD=CD=4a,
∵E为边AD的中点,CF=3FD,
∴AE=DE=2a,DF=a,
∴,
∴
又∵∠A=∠D=90°
∴△ABE∽△DEF.
(2)∵△ABE∽△DEF,
∴
∴∠AEB=∠DFE∠ABE=∠DEF
∵∠AEB+∠ABE=90°,
∴∠BEF=90°
又∵,∠A=90°
∴,∠A=∠BEF=90°
∴△ABE∽△EBF.
6.证明:(1)连接OD,BC,OD与BC相交于点G,
∵D是弧BC的中点,
∴OD垂直平分BC,
∵AB为⊙O的直径,
∴AC⊥BC,
∴OD∥AE,
∵DE⊥AC,
∴OD⊥DE,
∵OD为⊙O的半径,
∴DE是⊙O的切线;
(2)由(1)知:OD⊥BC,AC⊥BC,DE⊥AC,
∴四边形DECG为矩形,
∴CG=DE=4,
∴BC=8,
∵⊙O的半径为5,
∴AB=10,
∴AC==6,
OG=AC=3,GD=2,在矩形GDEC中
CE=GD=2,
∴AE=8.
∵D为弧BC的中点,
∴∠EAD=∠FAB,
∵BF切⊙O于B,
∴∠FBA=90°.
又∵DE⊥AC于E,
∴∠E=90°,
∴∠FBA=∠E,
∴△AED∽△ABF,
∴,
∴
∴BF=5.
7.(1)证明:∵四边形ABCD是正方形,
∴∠ABC=90°,
∵EF⊥AC,
∴∠FEC=90°=∠ABC,
又∵∠FCE=∠ACB,
∴△CEF∽△CBA,
∴=,
又∵∠ACF=∠BCE,
∴△CAF∽△CBE;
(2)∵△CAF∽△CBE,
∴∠CAF=∠CBE,
∵AF平分∠BAC,
∴∠BAF=∠CAF,
∴∠BAF=∠CBE,
∴∠BAF+∠AFB=∠CBE+∠AFB=90°,
即∠ABF=∠BGA=90°,
∵∠BAG=∠BAF,
∴△ABF∽△AGB,
∴=,
∴AB2=AG?AF,
∵正方形ABCD中,AC2=2AB2,
∴AC2=2AG?AF
8.证明:(1)∵△ABC中,AB=AC,
∴∠B=∠C,
∵∠B+∠BDE+∠DEB=180°,∠BDE+∠EDF+∠FDC=180°,∠EDF=∠B,
∴∠FDC=∠DEB,
∴△BDE∽△CFD,
∴,
即DE?CD=DF?BE;
(2)由(1)可得:△BDE∽△CFD,
∴,
∵D为BC中点,
∴BD=CD,
∴,
∵∠B=∠EDF,
∴△BDE∽△DFE,
∴∠BED=∠DEF,
∴ED平分∠BEF.
9.解:(1)∵∠A=30°,∠C=90°,AB=12,EF=x,四边形CDEF为矩形,
∴∠AFE=90°,AE=2x,AF==x,
同理:AC=6,
∴CF=6﹣x,
∵矩形CDEF的面积为8,
∴x(6﹣x)=8,
解得:x=2或4;
故x的值为2或4;
(2)不能,
理由是:由(1)知:S矩形CDEF=x(6﹣x)
若S矩形CDEF=10,即x(6﹣x)=10,
即x2﹣6x+10=0,
∵△=62﹣4×1×10=﹣4<0,
∴此方程无解,
故矩形面积不能为10.
10.解:∵ABCD是正方形,
∴∠A=∠B=90°,
∴∠ADE+∠DEA=90°,
又EF⊥DE,
∴∠AED+∠FEB=90°,
∴∠ADE=∠FEB,
∴△ADE∽△BEF.
∴=,
∴=,
∴BF=
∵BC=8,
∴CF=BC﹣BF=.
《相似
》
章节培优训练(一)
1.已知:如图,D、E分别是△ABC的边AB、AC上的点,且∠AED=∠ABC,联结BE、CD相交于点F.
(1)求证:∠ABE=∠ACD;
(2)如果ED=EC,求证:.
2.如图,在△ABC中,点D在边AB上,点E、点F在边AC上,且DE∥BC,=.
(1)求证:DF∥BE;
(2)如果AF=2,EF=4,AB=6,求的值.
3.已知:如图,在四边形ABCD中,AB=AD,AC、BD相交于点E,AE?CE=DE?BE
(1)求证:△ABE∽△ACB;
(2)如果DA2=DE?DB,求证:AB?EC=BC?AE.
4.(1)如图1,已知AB⊥l,DE⊥l,垂足分别为B、E,且C是l上一点,∠ACD=90°,求证:△ABC∽△CED;
(2)如图2,在四边形ABCD中,已知∠ABC=90°,AB=3,BC=4,CD=10,DA=5,求BD的长.
5.如图,在正方形ABCD中,E是AD的中点,点F在CD上,且CF=3FD.
(1)求证:△ABE∽△DEF;
(2)△ABE与△BEF相似吗?为什么?
6.如图,AB为⊙O的直径,D是弧BC的中点,DE⊥AC交AC的延长线于E,⊙O的切线BF交AD的延长线于F.
(1)求证:DE是⊙O的切线;
(2)若DE=4,⊙O的半径为5.求BF的长.
7.如图,点E是正方形ABCD的对角线AC上的一个动点(不与A、C重合),作EF⊥AC交边BC于点F,连接AF、BE交于点G.
(1)求证:△CAF∽△CBE;
(2)若AF平分∠BAC,求证:AC2=2AG?AF.
8.△ABC中,AB=AC,点D、E、F分别在BC、AB、AC上,∠EDF=∠B.
(1)如图1,求证:DE?CD=DF?BE;
(2)如图2,若D为BC中点,连接EF.求证:ED平分∠BEF.
9.一块三角形材料如图所示,∠A=30°,∠C=90°,AB=12,用这块材料剪出一个矩形CDEF,其中点D、E、F分别在BC、AB、AC上.设EF=x,请解答下列问题:
(1)若矩形CDEF的面积为8,求x的值;
(2)矩形CDEF的面积能否为10?给出你的结论并说明理由.
10.如图,E是边长为8的正方形ABCD的边AB上的点,且AE=2,EF⊥DE交BC于点F.求线段CF的长.
参考答案
1.(1)证明:∵∠AED=∠ABC,∠A=∠A,
∴△ADE∽△ACB,
∴=,
∵∠A=∠A,
∴△ADC∽△AEB,
∴∠ABE=∠ACD;
(2)证明:∵ED=EC,
∴∠EDC=∠ECD,
∴∠EDC=∠EBD,
∵∠DEF=∠DEB,
∴△EDF∽△EBD,
∴==,
()2=?,
∴.
2.(1)证明:∵DE∥BC,
∴=,
∵=,
∴=,
∴DF∥BE;
(2)解:∵AF=2,EF=4,
∴AE=AF+EF=6,==,
∴=,
∴AD=AB=2,BD=2AD=4,
∴==,
∵==,
∴=,
又∵∠A=∠A,
∴△ADE∽△AEB,
∴==.
3.证明:(1)∵AE?CE=DE?BE,∠AED=∠BEC,
∴△ADE∽△CBE,
∴∠DAE=∠CBE,∠ADE=∠BCE,
∵AB=AD,
∴∠ADB=∠ABE,
∴∠ABE=∠ACB,
∵∠BAE=∠CAB,
∴△ABE∽△ACB;
(2)∵DA2=DE?DB,∠ADB=∠ADE,
∴△ADB∽△ADE,
∴=,
∵△ABE∽△ACB,
∴=,
∴AD=,
∴==,
∴AB?EC=BC?AE.
4.证明:(1)∵AB⊥l,DE⊥l,
∴∠ABC=∠CED=90°,∠ACB+∠BAC=90°,
∵∠ACD=90°,
∴∠ACB+∠DCE=90°,
∴∠BAC=∠DCE,
∴△ABC∽△CED;
(2)如图,连接AC,
∵∠ABC=90°,
∴AC=,
∵AD=5,CD=10,
∴△ACD满足AC2+CD2=AD2,
∴∠ACD=90°,
如图,过点D作DE⊥BC延长线于点E,
由(1)得此时△ABC∽△CED,
∴,
∴CE=6,DE=8,
在Rt△BDE中,BD=.
5.证明:(1)∵四边形ABCD为正方形,
∴∠A=∠D=90°,AB=AD=CD,
设AB=AD=CD=4a,
∵E为边AD的中点,CF=3FD,
∴AE=DE=2a,DF=a,
∴,
∴
又∵∠A=∠D=90°
∴△ABE∽△DEF.
(2)∵△ABE∽△DEF,
∴
∴∠AEB=∠DFE∠ABE=∠DEF
∵∠AEB+∠ABE=90°,
∴∠BEF=90°
又∵,∠A=90°
∴,∠A=∠BEF=90°
∴△ABE∽△EBF.
6.证明:(1)连接OD,BC,OD与BC相交于点G,
∵D是弧BC的中点,
∴OD垂直平分BC,
∵AB为⊙O的直径,
∴AC⊥BC,
∴OD∥AE,
∵DE⊥AC,
∴OD⊥DE,
∵OD为⊙O的半径,
∴DE是⊙O的切线;
(2)由(1)知:OD⊥BC,AC⊥BC,DE⊥AC,
∴四边形DECG为矩形,
∴CG=DE=4,
∴BC=8,
∵⊙O的半径为5,
∴AB=10,
∴AC==6,
OG=AC=3,GD=2,在矩形GDEC中
CE=GD=2,
∴AE=8.
∵D为弧BC的中点,
∴∠EAD=∠FAB,
∵BF切⊙O于B,
∴∠FBA=90°.
又∵DE⊥AC于E,
∴∠E=90°,
∴∠FBA=∠E,
∴△AED∽△ABF,
∴,
∴
∴BF=5.
7.(1)证明:∵四边形ABCD是正方形,
∴∠ABC=90°,
∵EF⊥AC,
∴∠FEC=90°=∠ABC,
又∵∠FCE=∠ACB,
∴△CEF∽△CBA,
∴=,
又∵∠ACF=∠BCE,
∴△CAF∽△CBE;
(2)∵△CAF∽△CBE,
∴∠CAF=∠CBE,
∵AF平分∠BAC,
∴∠BAF=∠CAF,
∴∠BAF=∠CBE,
∴∠BAF+∠AFB=∠CBE+∠AFB=90°,
即∠ABF=∠BGA=90°,
∵∠BAG=∠BAF,
∴△ABF∽△AGB,
∴=,
∴AB2=AG?AF,
∵正方形ABCD中,AC2=2AB2,
∴AC2=2AG?AF
8.证明:(1)∵△ABC中,AB=AC,
∴∠B=∠C,
∵∠B+∠BDE+∠DEB=180°,∠BDE+∠EDF+∠FDC=180°,∠EDF=∠B,
∴∠FDC=∠DEB,
∴△BDE∽△CFD,
∴,
即DE?CD=DF?BE;
(2)由(1)可得:△BDE∽△CFD,
∴,
∵D为BC中点,
∴BD=CD,
∴,
∵∠B=∠EDF,
∴△BDE∽△DFE,
∴∠BED=∠DEF,
∴ED平分∠BEF.
9.解:(1)∵∠A=30°,∠C=90°,AB=12,EF=x,四边形CDEF为矩形,
∴∠AFE=90°,AE=2x,AF==x,
同理:AC=6,
∴CF=6﹣x,
∵矩形CDEF的面积为8,
∴x(6﹣x)=8,
解得:x=2或4;
故x的值为2或4;
(2)不能,
理由是:由(1)知:S矩形CDEF=x(6﹣x)
若S矩形CDEF=10,即x(6﹣x)=10,
即x2﹣6x+10=0,
∵△=62﹣4×1×10=﹣4<0,
∴此方程无解,
故矩形面积不能为10.
10.解:∵ABCD是正方形,
∴∠A=∠B=90°,
∴∠ADE+∠DEA=90°,
又EF⊥DE,
∴∠AED+∠FEB=90°,
∴∠ADE=∠FEB,
∴△ADE∽△BEF.
∴=,
∴=,
∴BF=
∵BC=8,
∴CF=BC﹣BF=.
