2020-2021学年人教版数学九年级下册第27章 《相似 》章节 训练(二)(Word版 含答案)
文档属性
| 名称 | 2020-2021学年人教版数学九年级下册第27章 《相似 》章节 训练(二)(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 132.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 00:00:00 | ||
图片预览




文档简介
九年级下册第27章
《相似
》
章节培优训练(二)
1.如图1,△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE.
(1)求证:BD=CE;
(2)若点M,N分别是BD,CE的中点,如图2,连接AM,AN,MN
①求证:△AMN∽△ABC;
②若AC=6,AE=4,∠EAC=60°,求AN的长.
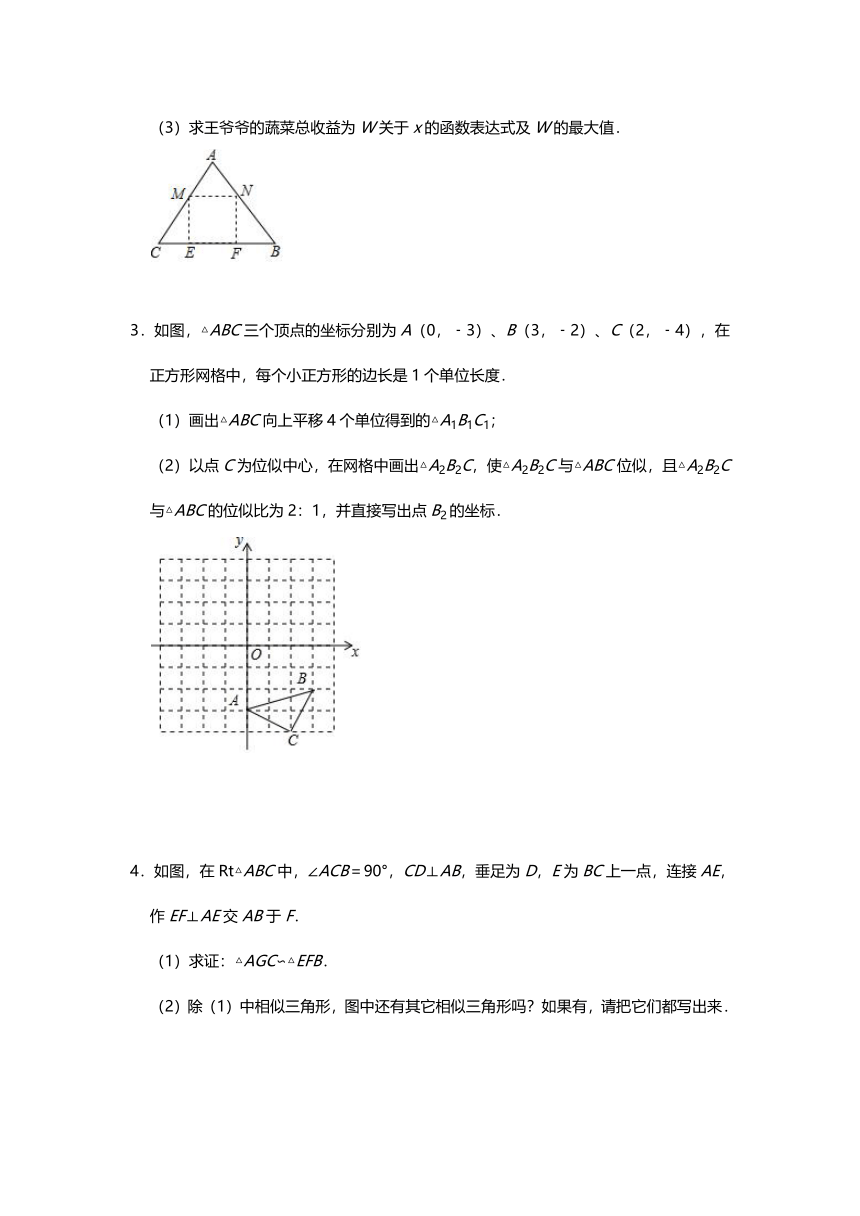
2.如图,王爷爷家院子里有一块三角形田地ABC,AB=AC=5米,BC=6米,现打算把它开垦出一个矩形MNFE区域种植韭菜,△AMN区域种植芹菜,△CME和△BNF区域种植青菜(开垦土地面积损耗均忽略不计),其中点M,N分别在AC,AB上,点E,F在BC上,已知韭菜每平方米收益100元,芹菜每平方米收益60元,青菜每平方米收益40元,设CM=5x米,王爷爷的蔬菜总收益为W元.
(1)当矩形MNFE恰好为正方形时,求韭菜种植区域矩形MNFE的面积.
(2)若种植韭菜的收益等于另两种蔬菜收益之和的2倍,求这时x的值.
(3)求王爷爷的蔬菜总收益为W关于x的函数表达式及W的最大值.
3.如图,△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),在正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移4个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C,使△A2B2C与△ABC位似,且△A2B2C与△ABC的位似比为2:1,并直接写出点B2的坐标.
4.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,E为BC上一点,连接AE,作EF⊥AE交AB于F.
(1)求证:△AGC∽△EFB.
(2)除(1)中相似三角形,图中还有其它相似三角形吗?如果有,请把它们都写出来.
5.如图,在△ABC中,D为AB边上一点,E为AC边上一点,且
(1)求证:△ADE∽△ABC;
(2)求△ADE与四边形DBCE的面积比.
6.如图,AC是?ABCD的对角线,在AD边上取一点F,连接BF交AC于点E,并延长BF交CD的延长线于点G.
(1)若∠ABF=∠ACF,求证:CE2=EF?EG;
(2)若DG=DC,BE=6,求EF的长.
7.已知:如图,在平行四边形ABCD中,AC为对角线,E是边AD上一点,BE⊥AC交AC于点F,BE、CD的延长线交于点G,且∠ABE=∠CAD.
(1)求证:四边形ABCD是矩形;
(2)如果AE=EG,求证:AC2=BC?BG.
8.如图,已知在梯形ABCD中,AD∥BC,∠A=90°,AB=AD,点E在边AB上,且DE⊥CD,DF平分∠EDC,交BC于点F,联结CE、EF.
(1)求证:DE=DC;
(2)如果BE2=BF?BC,求证:∠BEF=∠CEF.
9.在△ABC中,BC=2,BC边上的高AD=1,P是BC上任一点,PE∥AB交AC于E,PF∥AC交AB于F.
(1)设BP=x,将S△PEF用x表示;
(2)当P在BC边上什么位置时,S值最大.
10.如图,在Rt△ABC中,∠B=90°,AB=9cm,BC=2cm,点M,N分别从A,B同时出发,M在AB边上沿AB方向以每秒2cm的速度匀速运动,N在BC边上沿BC方向以每秒1cm的速度匀速运动(当点N运动到点C时,两点同时停止运动).设运动时间为x秒,△MBN的面积为ycm2.
(1)求y与x之间的函数关系式,并直接写出自变量x的取值范围;
(2)求△MBN的面积的最大值.
参考答案
1.解:(1)∵∠BAC=∠DAE,
∴∠BAC﹣∠BAE=∠DAE﹣∠BAE,
∴∠EAC=∠DAB,
∵AB=AC、AD=AE,
∴△CAE≌△BAD,
∴BD=CE;
(2)①由△CAE≌△BAD知∠ACE=∠ABD,
∵点M、N分别是BD、CE的中点,CE=BD,
∴CN=BM,
∴△CAN≌△BAM,
∴AN=AM、∠CAN=∠BAM,
∴∠CAN+∠BAN=∠BAM+∠BAN,即∠CAB=∠NAM,
∵AC=AB、AN=AM,
∴=,
∴△AMN∽△ABC;
②取AC的中点F,连接FN,过点N作NG⊥AC于点G,
∵N是CE的中点,
∴NF∥AE,NF=AE=2,
∴∠GFN=∠EAC=60°,
∴∠FNG=30°,
∴FG=FN=1,
∴AG=1+3=4,NG==,
在Rt△ANG中,由勾股定理可得AN==.
2.解:(1)作AH⊥BC于H,交MN于D.
∵AB=AC,AH⊥BC,
∴CH=HB=3,
在Rt△ACH中,AH==4,
∵ME∥AH,
∴==,
∴CE=3x,EM=EF=4x,
易证△MEC≌△NFB,
∴CE=BF=3x,
∴3x+4x+3x=6,
∴x=,
∴EM=,
∴矩形MNFE的面积为平方米.
(2)由题意:100×4x?(6﹣6x)=2?[60××(6﹣6x)?(4﹣4x)+40×4x×3x],
解得x=或.
(3)由题意W=100×4x?(6﹣6x)+60××(6﹣6x)?(4﹣4x)+40×4x×3x=﹣1200x2+960x+720=﹣1200(x﹣)2+912,
,∵﹣1200<0,
∴x=时,W有最大值,最大值为912元.
3.解:(1)如图所示,△A1B1C1为所求的三角形;
(2)如图所示,△A2B2C为所求三角形,点B2的坐标为(4,0).
4.(1)证明
∵CD⊥AB,EF⊥AE
∴∠FDG=∠FEG=90°
∴∠DGE+∠DFE=360°﹣90°﹣90°=180°
又∠BFE+∠DFE=180°,
∴∠BFE=∠DGE,
又∠DGE=∠AGC
∴∠AGC=∠BFE,
又∠ACB=∠FEG=90°
∴∠AEC+∠BEF=180°﹣90°=90°,∠AEC+∠EAC=90°,
∴∠EAC=∠BEF,
∴△AGC∽△EFB;
(2)有.
∵∠GAD=∠FAE,∠ADG=∠AEF=90°,
∴△AGD∽△AFE;
∴∠CAD=∠BAC,
∴△ACD∽△ABC,
同理得△BCD∽△BAC,
∴△ACD∽△CBD,
即△ACD∽△ABC∽△CBD,
5.(1)证明:∵,
∴==,
∵∠A=∠A,
∴△ADE∽△ABC;
(2)解:∵△ADE∽△ABC,=,
∴=()2=,
∴△ADE与四边形DBCE的面积比是4:5.
6.解:(1)∵AB∥CG,
∴∠ABF=∠G,
又∵∠ABF=∠ACF,
∴∠ECF=∠G,
又∵∠CEF=∠CEG,
∴△ECF∽△EGC,
∴,即CE2=EF?EG;
(2)∵平行四边形ABCD中,AB=CD,
又∵DG=DC,
∴AB=CD=DG,
∴AB:CG=1:2,
∵AB∥CG,
∴,
即,
∴EG=12,BG=18,
∵AB∥DG,
∴,
∴BF=BG=9,
∴EF=BF﹣BE=9﹣6=3.
7.解:
(1)证明:
∵BE⊥AC,
∴∠AFB=90°.
∴∠ABE+∠BAF=90°.
∵∠ABE=∠CAD.
∴∠CAD+∠BAF=90°.
即∠BAD=90°.
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形;
(2)连接AG.
∵AE=EG,
∴∠EAG=∠EGA.
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC.
∴∠ABG=∠BGC.
∴∠CAD=∠BGC.
∴∠AGC=∠GAC.
∴CA=CG.
∵AD∥BC,
∴∠CAD=∠ACB.
∴∠ACB=∠BGC.
∵四边形ABCD是矩形,
∴∠BCG=90°.
∴∠BCG=∠ABC,
∴△BCG∽△ABC.
∴.
∴AC2=BC?BG.
8.(1)证明:过D作DG⊥BC于G,
∵AD∥BC,∠A=90°,
∴∠B=90°,
∴四边形ABGD是矩形,
∴∠ADG=90°,DG=AB,
∵∠EDC=90°,
∴∠ADE=∠CDG,
在△AED与△GCD中,
,
∴△AED≌△GCD,
∴DE=CD;
(2)由(1)知:DE=CD,
∵DF平分∠EDC,
∴DF⊥CE,
∴EF=CF,
∴∠FEC=∠FCE,
∵BE2=BF?BC,
∴=,∵∠B=∠B,
∴△EFB∽△CEB,
∴∠BEF=∠FCE,
∴∠BEF=∠CEF.
9.解:(1)∵BC=2,BC边上的高AD=1,
∴S△ABC=×2×1=1,
∵BP=x,
∴PC=2﹣x,
∵PE∥AB,
∴△CEP与△CAB相似,
∴=()2,
∴S△CEP=1﹣x+,
同理,得到S△BPF=,
∵四边形AEPF为平行四边形,
∴S△PEF=S?AEPF=(S△ABC﹣S△CEP﹣S△BPF)
=﹣x2+x(0<x<2).
S△PEF=﹣x2+x(0<x<2).
(2)由(1)知S△PEF=﹣x2+x=﹣(x﹣1)2+,
∵0<x<2,
∴当x=1时,面积有最大值.
10.解:(1)设运动时间为x秒,△MBN的面积为ycm2,
则AM=2x,BM=9﹣2x,BN=x,
根据题意得:y=BM?BN=(9﹣2x)x,
∴y=﹣x2+x,(0<x≤2);
(2)由(1)得,y=﹣x2+x,
对称轴为;x=>2,
∵当x,y随x的增大而增大,
又∵0<x≤2,
∴当x=2时,y最大=5,
∴△MBN的面积的最大值是5.
《相似
》
章节培优训练(二)
1.如图1,△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE.
(1)求证:BD=CE;
(2)若点M,N分别是BD,CE的中点,如图2,连接AM,AN,MN
①求证:△AMN∽△ABC;
②若AC=6,AE=4,∠EAC=60°,求AN的长.
2.如图,王爷爷家院子里有一块三角形田地ABC,AB=AC=5米,BC=6米,现打算把它开垦出一个矩形MNFE区域种植韭菜,△AMN区域种植芹菜,△CME和△BNF区域种植青菜(开垦土地面积损耗均忽略不计),其中点M,N分别在AC,AB上,点E,F在BC上,已知韭菜每平方米收益100元,芹菜每平方米收益60元,青菜每平方米收益40元,设CM=5x米,王爷爷的蔬菜总收益为W元.
(1)当矩形MNFE恰好为正方形时,求韭菜种植区域矩形MNFE的面积.
(2)若种植韭菜的收益等于另两种蔬菜收益之和的2倍,求这时x的值.
(3)求王爷爷的蔬菜总收益为W关于x的函数表达式及W的最大值.
3.如图,△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),在正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移4个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C,使△A2B2C与△ABC位似,且△A2B2C与△ABC的位似比为2:1,并直接写出点B2的坐标.
4.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,E为BC上一点,连接AE,作EF⊥AE交AB于F.
(1)求证:△AGC∽△EFB.
(2)除(1)中相似三角形,图中还有其它相似三角形吗?如果有,请把它们都写出来.
5.如图,在△ABC中,D为AB边上一点,E为AC边上一点,且
(1)求证:△ADE∽△ABC;
(2)求△ADE与四边形DBCE的面积比.
6.如图,AC是?ABCD的对角线,在AD边上取一点F,连接BF交AC于点E,并延长BF交CD的延长线于点G.
(1)若∠ABF=∠ACF,求证:CE2=EF?EG;
(2)若DG=DC,BE=6,求EF的长.
7.已知:如图,在平行四边形ABCD中,AC为对角线,E是边AD上一点,BE⊥AC交AC于点F,BE、CD的延长线交于点G,且∠ABE=∠CAD.
(1)求证:四边形ABCD是矩形;
(2)如果AE=EG,求证:AC2=BC?BG.
8.如图,已知在梯形ABCD中,AD∥BC,∠A=90°,AB=AD,点E在边AB上,且DE⊥CD,DF平分∠EDC,交BC于点F,联结CE、EF.
(1)求证:DE=DC;
(2)如果BE2=BF?BC,求证:∠BEF=∠CEF.
9.在△ABC中,BC=2,BC边上的高AD=1,P是BC上任一点,PE∥AB交AC于E,PF∥AC交AB于F.
(1)设BP=x,将S△PEF用x表示;
(2)当P在BC边上什么位置时,S值最大.
10.如图,在Rt△ABC中,∠B=90°,AB=9cm,BC=2cm,点M,N分别从A,B同时出发,M在AB边上沿AB方向以每秒2cm的速度匀速运动,N在BC边上沿BC方向以每秒1cm的速度匀速运动(当点N运动到点C时,两点同时停止运动).设运动时间为x秒,△MBN的面积为ycm2.
(1)求y与x之间的函数关系式,并直接写出自变量x的取值范围;
(2)求△MBN的面积的最大值.
参考答案
1.解:(1)∵∠BAC=∠DAE,
∴∠BAC﹣∠BAE=∠DAE﹣∠BAE,
∴∠EAC=∠DAB,
∵AB=AC、AD=AE,
∴△CAE≌△BAD,
∴BD=CE;
(2)①由△CAE≌△BAD知∠ACE=∠ABD,
∵点M、N分别是BD、CE的中点,CE=BD,
∴CN=BM,
∴△CAN≌△BAM,
∴AN=AM、∠CAN=∠BAM,
∴∠CAN+∠BAN=∠BAM+∠BAN,即∠CAB=∠NAM,
∵AC=AB、AN=AM,
∴=,
∴△AMN∽△ABC;
②取AC的中点F,连接FN,过点N作NG⊥AC于点G,
∵N是CE的中点,
∴NF∥AE,NF=AE=2,
∴∠GFN=∠EAC=60°,
∴∠FNG=30°,
∴FG=FN=1,
∴AG=1+3=4,NG==,
在Rt△ANG中,由勾股定理可得AN==.
2.解:(1)作AH⊥BC于H,交MN于D.
∵AB=AC,AH⊥BC,
∴CH=HB=3,
在Rt△ACH中,AH==4,
∵ME∥AH,
∴==,
∴CE=3x,EM=EF=4x,
易证△MEC≌△NFB,
∴CE=BF=3x,
∴3x+4x+3x=6,
∴x=,
∴EM=,
∴矩形MNFE的面积为平方米.
(2)由题意:100×4x?(6﹣6x)=2?[60××(6﹣6x)?(4﹣4x)+40×4x×3x],
解得x=或.
(3)由题意W=100×4x?(6﹣6x)+60××(6﹣6x)?(4﹣4x)+40×4x×3x=﹣1200x2+960x+720=﹣1200(x﹣)2+912,
,∵﹣1200<0,
∴x=时,W有最大值,最大值为912元.
3.解:(1)如图所示,△A1B1C1为所求的三角形;
(2)如图所示,△A2B2C为所求三角形,点B2的坐标为(4,0).
4.(1)证明
∵CD⊥AB,EF⊥AE
∴∠FDG=∠FEG=90°
∴∠DGE+∠DFE=360°﹣90°﹣90°=180°
又∠BFE+∠DFE=180°,
∴∠BFE=∠DGE,
又∠DGE=∠AGC
∴∠AGC=∠BFE,
又∠ACB=∠FEG=90°
∴∠AEC+∠BEF=180°﹣90°=90°,∠AEC+∠EAC=90°,
∴∠EAC=∠BEF,
∴△AGC∽△EFB;
(2)有.
∵∠GAD=∠FAE,∠ADG=∠AEF=90°,
∴△AGD∽△AFE;
∴∠CAD=∠BAC,
∴△ACD∽△ABC,
同理得△BCD∽△BAC,
∴△ACD∽△CBD,
即△ACD∽△ABC∽△CBD,
5.(1)证明:∵,
∴==,
∵∠A=∠A,
∴△ADE∽△ABC;
(2)解:∵△ADE∽△ABC,=,
∴=()2=,
∴△ADE与四边形DBCE的面积比是4:5.
6.解:(1)∵AB∥CG,
∴∠ABF=∠G,
又∵∠ABF=∠ACF,
∴∠ECF=∠G,
又∵∠CEF=∠CEG,
∴△ECF∽△EGC,
∴,即CE2=EF?EG;
(2)∵平行四边形ABCD中,AB=CD,
又∵DG=DC,
∴AB=CD=DG,
∴AB:CG=1:2,
∵AB∥CG,
∴,
即,
∴EG=12,BG=18,
∵AB∥DG,
∴,
∴BF=BG=9,
∴EF=BF﹣BE=9﹣6=3.
7.解:
(1)证明:
∵BE⊥AC,
∴∠AFB=90°.
∴∠ABE+∠BAF=90°.
∵∠ABE=∠CAD.
∴∠CAD+∠BAF=90°.
即∠BAD=90°.
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形;
(2)连接AG.
∵AE=EG,
∴∠EAG=∠EGA.
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC.
∴∠ABG=∠BGC.
∴∠CAD=∠BGC.
∴∠AGC=∠GAC.
∴CA=CG.
∵AD∥BC,
∴∠CAD=∠ACB.
∴∠ACB=∠BGC.
∵四边形ABCD是矩形,
∴∠BCG=90°.
∴∠BCG=∠ABC,
∴△BCG∽△ABC.
∴.
∴AC2=BC?BG.
8.(1)证明:过D作DG⊥BC于G,
∵AD∥BC,∠A=90°,
∴∠B=90°,
∴四边形ABGD是矩形,
∴∠ADG=90°,DG=AB,
∵∠EDC=90°,
∴∠ADE=∠CDG,
在△AED与△GCD中,
,
∴△AED≌△GCD,
∴DE=CD;
(2)由(1)知:DE=CD,
∵DF平分∠EDC,
∴DF⊥CE,
∴EF=CF,
∴∠FEC=∠FCE,
∵BE2=BF?BC,
∴=,∵∠B=∠B,
∴△EFB∽△CEB,
∴∠BEF=∠FCE,
∴∠BEF=∠CEF.
9.解:(1)∵BC=2,BC边上的高AD=1,
∴S△ABC=×2×1=1,
∵BP=x,
∴PC=2﹣x,
∵PE∥AB,
∴△CEP与△CAB相似,
∴=()2,
∴S△CEP=1﹣x+,
同理,得到S△BPF=,
∵四边形AEPF为平行四边形,
∴S△PEF=S?AEPF=(S△ABC﹣S△CEP﹣S△BPF)
=﹣x2+x(0<x<2).
S△PEF=﹣x2+x(0<x<2).
(2)由(1)知S△PEF=﹣x2+x=﹣(x﹣1)2+,
∵0<x<2,
∴当x=1时,面积有最大值.
10.解:(1)设运动时间为x秒,△MBN的面积为ycm2,
则AM=2x,BM=9﹣2x,BN=x,
根据题意得:y=BM?BN=(9﹣2x)x,
∴y=﹣x2+x,(0<x≤2);
(2)由(1)得,y=﹣x2+x,
对称轴为;x=>2,
∵当x,y随x的增大而增大,
又∵0<x≤2,
∴当x=2时,y最大=5,
∴△MBN的面积的最大值是5.
