6.4 密度知识的应用—-苏科版八年级物理下册课件28张
文档属性
| 名称 | 6.4 密度知识的应用—-苏科版八年级物理下册课件28张 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-02-21 09:22:54 | ||
图片预览








文档简介
6、4密度知识应用课件
学习目标
1、知道密度的意义,单位,能熟练的进行单位间的换算
2、知道密度公式的意义,能对公式进行变形,并能运用公式进行计算
3、知道密度知识的应用,能联系实际应用密度知识解决实际问题。
4、会测量固体和液体的密度。
物体质量与体积的比叫做组成这种物质的密度
二.密度的计算公式:
一、密度的定义:
质量
密度=————
体积
密度-ρ 质量-m 体积-V
m
则公式就为: ρ =——
V
换算关系:
常见的单位:克/厘米3 (g/cm3)
三.密度的单位:千克/米3 (kg/m3)
质量的单位:千克/kg
体积的单位:立方米/m3
密度的单位:千克/米3 (kg/m3)
水的密度为1.0x103千克/米3,表示的意思是?
1立方米水的质量为1.0x103千克
注:密度是物质的一种特性,通常可以用来鉴别一些物质。但会受一些外界因素的影响(如温度.压强.状态等)。在温度变化不大时由于固体和液体的热胀冷缩不大,我们可以认为密度不变(但气体影响明显)。
密度是物质的一种特性,同种物质的密度是相同的。
四、密度公式的应用:
1.计算物质的密度: ρ=m/V
计算密度.鉴别物质
2.计算物体的体积: V=m/ ρ
可以计算一些体积难以测量的物体
(如沙子、等一些形状不规则的物体)
3.计算物体的质量: m=ρV
(一)实验:测固体和液体的密度
实验原理:
实验器材:
用天平和量筒测出物体的质量和体积,
根据公式 算出物质密度。
ρ=
m
V
托盘天平、量筒、烧杯、水、待测物体
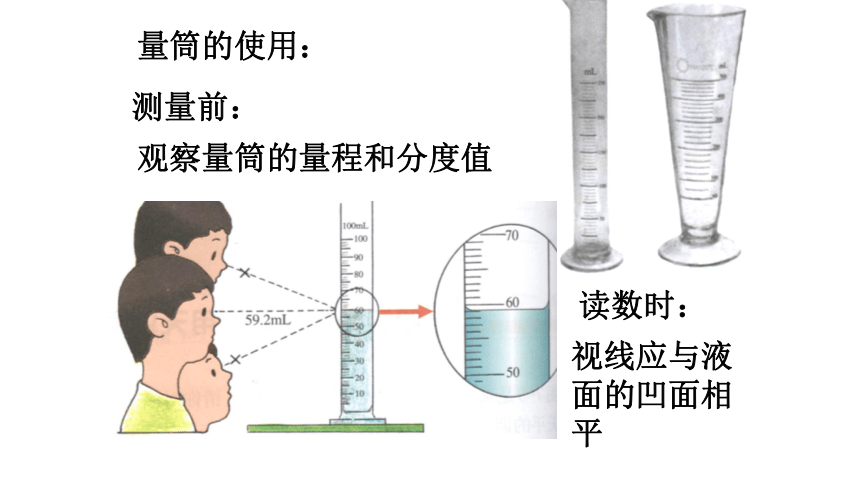
量筒的使用:
测量前:
读数时:
观察量筒的量程和分度值
视线应与液面的凹面相平
1、实验如何测固体(如小石块)的密度
1.用调好的天平测出石块的质量m
2.在量筒内倒入适量的水,测出水的体积V1
3.将石块浸没在量筒的水中,读出水面到达刻度V2
实验步骤:
4.石块的密度:
小石块的质量m(g)
水的体积V1
(m3)
水和石块的总体积V2
(m3)
石块的
体积V
(cm3)
石块的
密度ρ
(g/cm3)
实验表格:
测定盐水的密度
2、如何测液体的密度
1.用调好的天平测出烧杯和液体的总质量m1
2.将部分液体倒入量筒,测出液体的体积V
3.用天平测出烧杯和剩余液体的质量m2
实验步骤:
4.液体的密度:
V
m1-
V
m
=
r
m2
=
实验表格:
烧杯和酒精的总质量m1(g)
烧杯和剩余酒精的质量m2(g)
酒精的
质量
m(g)
量筒中酒精的体积V(m3)
酒精的
密度ρ
(g/cm3)
(二)密度公式的应用:
1.计算物质的密度: ρ=m/V
例:有一枚第十一届亚运会纪念币,它的质量为16 .1g,体积为1 .8cm3,试求制成这枚纪念币的金属密度,是何种金属?
计算密度.鉴别物质
2.计算物体的体积: V=m/ ρ
例:用天平称得一捆细铜丝的质量是445克,已知铜的密度是8.9×103千克/米3,这捆细铜丝的体积是多少?
可以计算一些体积难以测量的物体
(如沙子、等一些形状不规则的物体)
3.计算物体的质量: m=ρV
例:矗立在天安门广场的人民英雄纪念碑,它的碑心石是一块巨大的花岗岩,在长14.7m,宽2.9m,厚1m的碑心石上刻着“人民英雄永垂不朽”。怎样知道它的质量?
可以计算质量难以测量的物体
(如金字塔、人民英雄纪念碑等)
例2 一只铁球质量是3kg,体积是0.5dm3 试判断此铁球是空心的还是实心的.(已知铁的密度是 ρ=7.8×103kg/m3)
4、判断金属球是否为空心
经典命题训练
1、由铜、铁、铝、木四种材料做成的四个小球,测得其质量相等,体积也相等,则:( )
A、铜球一定是空心的 B、铁球可能是实心的C、铝球可能是实心的 D、木球一定是实心的
2、用铜和铝两种材料制成的导线.如果它们的质量和横截面积都相同.则这两条导线的长度之比等于(A )
A.27:89 B.89:27 C.1:3 D.3:1
3、分别用铝和铁做成一个实心球.在下列四种情况中,哪一种措施是不可能的?( )
A.铝球的体积和质量都比铁球小 B.铝球的体积和质量都比铁球大
C.铝球的体积大于铁球,但质量小于铁球 D.铝球的体积小于铁球,质量大于铁球
4、有甲、乙两个质量相等的实心正方体,甲的棱长是乙棱长的2倍,则甲的密度是乙密度的( )
A.2倍 B.8倍 C.1/2 倍 D.1/8倍
5、有两种材料制成的体积相同的甲乙两种实心球,在天平右盘里放2个甲球,在左盘中放3个乙球,天平恰好平衡,则 为( )
A.3:2 B.2:3 C.1:1 D.9:4
9、在用天平和量筒测量某种食油的密度时,以下操作步骤中,不必要且不合理的是()
A.用天平称出空烧杯的质量 B.取适量的油倒入烧杯,用天平测出杯和油的总质量
C.将烧杯中的油倒入量筒中,测出倒入量筒中油的体积 D.用天平称出烧杯和剩余油的总质量
10、小桅同学在实验室里将一金属块放在酒精灯上加热了一段时间,此时金属块的密度将_______(选填“变大”、“变小”或“不变”)。
11、1立方米的水结成冰后,体积增大了 ____________立方米。
12、小明在实验室里测量一块形状不规则、体积较大的矿石的密度,操作如下:
(1)用调节好的天平测量矿石的质量.当天平平衡时,右盘中砝码和游码的位置如图a所示,矿石的质量是_________ g.
(2)因矿石体积较大,放不进量筒,因此他利用了一只烧杯,按图b所示方法进行测量,矿石的体积是________ cm3.
(3)矿石的密度是_______ kg/m3,从图b中A到B的操作引起的密度测量值比它的真实值 __________ (选填“偏大”、“偏小”、“不变”) .
13、某同学在“测液体的密度”的实验中,测得的数据如右下表。
⑴该液体的密度是 _________kg/m3 ⑵表中的m值是 ______ g。
{5940675A-B579-460E-94D1-54222C63F5DA}液体和容器的总质量(g)
22
38
m
液体的体积(cm3)
15
35
40
14、小永同学为了测量永春老醋的密度,进行以下实验: 如图甲所示
(1)把天平放在_______,将游码移至零刻度处,然后调节_______,使天平横梁平衡。
(2)接下来进行以下3项操作:
A.用天平测量烧杯和剩余老醋的总质量m1;
B.将待测老醋倒入烧杯中,用天平测出烧杯和老醋的总质量m2;
C.将烧杯中老醋的一部分倒入量筒,测出这部分老醋的体积V;
以上操作的正确顺序是:_______________(填字母代号)。
(3)由图乙可知老醋的体积为_______㎝3,老醋的密度是_______g/㎝3 =_______㎏/m3。
一、质量相等问题:
1、三只完全相同的杯子中分别装有质量相等的水、煤油、硫酸,则液面最高的是 ________.
2、一块体积为100厘米3的冰块熔化成水后,体积多大?
计算典型专项练习册
二、体积相等问题:
1、某空瓶的质量为300 g,装满水后总质量为800g,若用该瓶装满某液体后总质量为850g,求瓶的容积与液体的密度。
2、某工程师为了减轻飞机的重量,将一钢制零件改成铝制零件,使其质量减少1.56Kg,则所需铝的质量为多少?(钢的密度为7.9×103Kg/cm3,铝的密度为2.7×103Kg/cm3)
三、密度相等问题:
1、地质队员测得一块巨石的体积为20m3,现从巨石上取得20cm3的样品,测得样品的质量为52g,求这块巨石的质量。
2、某同学在“测液体的密度”的实验中,
测得的数据如右下表。
⑴该液体的密度是 ________ kg/m3
⑵表中的m值是 _________ g。
{5940675A-B579-460E-94D1-54222C63F5DA}液体和容器的总质量(g)
22
38
m
液体的体积(cm3)
15
35
40
四、判断物体是空心还是实心问题
1、有一体积为30 cm3的空心铜球,它的质量为178g,铜的=8.9g/ cm3求(1)空心部分体积(2)若在空心部分装满水,求该球的总质量。
2、有一件标称纯金的工艺品,其质量100g,体积为6cm3,请你用两种方法判断它是否由纯金(不含有其他常见金属)制成的?
五、合金问题
1、用盐水选种需用密度是1.1×103kg/m3的盐水,现要配制500cm3的盐水,称得它的质量为600g,这样的盐水是否符合要求:如果不符合要求,需加盐还是加水?应该加多少?
2、为测定黄河水的含沙量,某校课外活动小组取了10dm3的黄河水,称其质量是10.18kg.已知沙子的密度沙=2.5×103kg/m3,问黄河水的含沙量是多少?(即每立方米黄河水中含沙多少千克)
3、按照行业规定:白酒的度数是指气温在20℃时,100ml酒中所含酒精的毫升数。请你根据行业规定计算白酒厂生产的每瓶“500ml 45°”的鲁源白酒的密度和质量分别是多少?(粗略认为白酒由纯水和酒精混合而成,不考虑混合时的体积变化)
学习目标
1、知道密度的意义,单位,能熟练的进行单位间的换算
2、知道密度公式的意义,能对公式进行变形,并能运用公式进行计算
3、知道密度知识的应用,能联系实际应用密度知识解决实际问题。
4、会测量固体和液体的密度。
物体质量与体积的比叫做组成这种物质的密度
二.密度的计算公式:
一、密度的定义:
质量
密度=————
体积
密度-ρ 质量-m 体积-V
m
则公式就为: ρ =——
V
换算关系:
常见的单位:克/厘米3 (g/cm3)
三.密度的单位:千克/米3 (kg/m3)
质量的单位:千克/kg
体积的单位:立方米/m3
密度的单位:千克/米3 (kg/m3)
水的密度为1.0x103千克/米3,表示的意思是?
1立方米水的质量为1.0x103千克
注:密度是物质的一种特性,通常可以用来鉴别一些物质。但会受一些外界因素的影响(如温度.压强.状态等)。在温度变化不大时由于固体和液体的热胀冷缩不大,我们可以认为密度不变(但气体影响明显)。
密度是物质的一种特性,同种物质的密度是相同的。
四、密度公式的应用:
1.计算物质的密度: ρ=m/V
计算密度.鉴别物质
2.计算物体的体积: V=m/ ρ
可以计算一些体积难以测量的物体
(如沙子、等一些形状不规则的物体)
3.计算物体的质量: m=ρV
(一)实验:测固体和液体的密度
实验原理:
实验器材:
用天平和量筒测出物体的质量和体积,
根据公式 算出物质密度。
ρ=
m
V
托盘天平、量筒、烧杯、水、待测物体
量筒的使用:
测量前:
读数时:
观察量筒的量程和分度值
视线应与液面的凹面相平
1、实验如何测固体(如小石块)的密度
1.用调好的天平测出石块的质量m
2.在量筒内倒入适量的水,测出水的体积V1
3.将石块浸没在量筒的水中,读出水面到达刻度V2
实验步骤:
4.石块的密度:
小石块的质量m(g)
水的体积V1
(m3)
水和石块的总体积V2
(m3)
石块的
体积V
(cm3)
石块的
密度ρ
(g/cm3)
实验表格:
测定盐水的密度
2、如何测液体的密度
1.用调好的天平测出烧杯和液体的总质量m1
2.将部分液体倒入量筒,测出液体的体积V
3.用天平测出烧杯和剩余液体的质量m2
实验步骤:
4.液体的密度:
V
m1-
V
m
=
r
m2
=
实验表格:
烧杯和酒精的总质量m1(g)
烧杯和剩余酒精的质量m2(g)
酒精的
质量
m(g)
量筒中酒精的体积V(m3)
酒精的
密度ρ
(g/cm3)
(二)密度公式的应用:
1.计算物质的密度: ρ=m/V
例:有一枚第十一届亚运会纪念币,它的质量为16 .1g,体积为1 .8cm3,试求制成这枚纪念币的金属密度,是何种金属?
计算密度.鉴别物质
2.计算物体的体积: V=m/ ρ
例:用天平称得一捆细铜丝的质量是445克,已知铜的密度是8.9×103千克/米3,这捆细铜丝的体积是多少?
可以计算一些体积难以测量的物体
(如沙子、等一些形状不规则的物体)
3.计算物体的质量: m=ρV
例:矗立在天安门广场的人民英雄纪念碑,它的碑心石是一块巨大的花岗岩,在长14.7m,宽2.9m,厚1m的碑心石上刻着“人民英雄永垂不朽”。怎样知道它的质量?
可以计算质量难以测量的物体
(如金字塔、人民英雄纪念碑等)
例2 一只铁球质量是3kg,体积是0.5dm3 试判断此铁球是空心的还是实心的.(已知铁的密度是 ρ=7.8×103kg/m3)
4、判断金属球是否为空心
经典命题训练
1、由铜、铁、铝、木四种材料做成的四个小球,测得其质量相等,体积也相等,则:( )
A、铜球一定是空心的 B、铁球可能是实心的C、铝球可能是实心的 D、木球一定是实心的
2、用铜和铝两种材料制成的导线.如果它们的质量和横截面积都相同.则这两条导线的长度之比等于(A )
A.27:89 B.89:27 C.1:3 D.3:1
3、分别用铝和铁做成一个实心球.在下列四种情况中,哪一种措施是不可能的?( )
A.铝球的体积和质量都比铁球小 B.铝球的体积和质量都比铁球大
C.铝球的体积大于铁球,但质量小于铁球 D.铝球的体积小于铁球,质量大于铁球
4、有甲、乙两个质量相等的实心正方体,甲的棱长是乙棱长的2倍,则甲的密度是乙密度的( )
A.2倍 B.8倍 C.1/2 倍 D.1/8倍
5、有两种材料制成的体积相同的甲乙两种实心球,在天平右盘里放2个甲球,在左盘中放3个乙球,天平恰好平衡,则 为( )
A.3:2 B.2:3 C.1:1 D.9:4
9、在用天平和量筒测量某种食油的密度时,以下操作步骤中,不必要且不合理的是()
A.用天平称出空烧杯的质量 B.取适量的油倒入烧杯,用天平测出杯和油的总质量
C.将烧杯中的油倒入量筒中,测出倒入量筒中油的体积 D.用天平称出烧杯和剩余油的总质量
10、小桅同学在实验室里将一金属块放在酒精灯上加热了一段时间,此时金属块的密度将_______(选填“变大”、“变小”或“不变”)。
11、1立方米的水结成冰后,体积增大了 ____________立方米。
12、小明在实验室里测量一块形状不规则、体积较大的矿石的密度,操作如下:
(1)用调节好的天平测量矿石的质量.当天平平衡时,右盘中砝码和游码的位置如图a所示,矿石的质量是_________ g.
(2)因矿石体积较大,放不进量筒,因此他利用了一只烧杯,按图b所示方法进行测量,矿石的体积是________ cm3.
(3)矿石的密度是_______ kg/m3,从图b中A到B的操作引起的密度测量值比它的真实值 __________ (选填“偏大”、“偏小”、“不变”) .
13、某同学在“测液体的密度”的实验中,测得的数据如右下表。
⑴该液体的密度是 _________kg/m3 ⑵表中的m值是 ______ g。
{5940675A-B579-460E-94D1-54222C63F5DA}液体和容器的总质量(g)
22
38
m
液体的体积(cm3)
15
35
40
14、小永同学为了测量永春老醋的密度,进行以下实验: 如图甲所示
(1)把天平放在_______,将游码移至零刻度处,然后调节_______,使天平横梁平衡。
(2)接下来进行以下3项操作:
A.用天平测量烧杯和剩余老醋的总质量m1;
B.将待测老醋倒入烧杯中,用天平测出烧杯和老醋的总质量m2;
C.将烧杯中老醋的一部分倒入量筒,测出这部分老醋的体积V;
以上操作的正确顺序是:_______________(填字母代号)。
(3)由图乙可知老醋的体积为_______㎝3,老醋的密度是_______g/㎝3 =_______㎏/m3。
一、质量相等问题:
1、三只完全相同的杯子中分别装有质量相等的水、煤油、硫酸,则液面最高的是 ________.
2、一块体积为100厘米3的冰块熔化成水后,体积多大?
计算典型专项练习册
二、体积相等问题:
1、某空瓶的质量为300 g,装满水后总质量为800g,若用该瓶装满某液体后总质量为850g,求瓶的容积与液体的密度。
2、某工程师为了减轻飞机的重量,将一钢制零件改成铝制零件,使其质量减少1.56Kg,则所需铝的质量为多少?(钢的密度为7.9×103Kg/cm3,铝的密度为2.7×103Kg/cm3)
三、密度相等问题:
1、地质队员测得一块巨石的体积为20m3,现从巨石上取得20cm3的样品,测得样品的质量为52g,求这块巨石的质量。
2、某同学在“测液体的密度”的实验中,
测得的数据如右下表。
⑴该液体的密度是 ________ kg/m3
⑵表中的m值是 _________ g。
{5940675A-B579-460E-94D1-54222C63F5DA}液体和容器的总质量(g)
22
38
m
液体的体积(cm3)
15
35
40
四、判断物体是空心还是实心问题
1、有一体积为30 cm3的空心铜球,它的质量为178g,铜的=8.9g/ cm3求(1)空心部分体积(2)若在空心部分装满水,求该球的总质量。
2、有一件标称纯金的工艺品,其质量100g,体积为6cm3,请你用两种方法判断它是否由纯金(不含有其他常见金属)制成的?
五、合金问题
1、用盐水选种需用密度是1.1×103kg/m3的盐水,现要配制500cm3的盐水,称得它的质量为600g,这样的盐水是否符合要求:如果不符合要求,需加盐还是加水?应该加多少?
2、为测定黄河水的含沙量,某校课外活动小组取了10dm3的黄河水,称其质量是10.18kg.已知沙子的密度沙=2.5×103kg/m3,问黄河水的含沙量是多少?(即每立方米黄河水中含沙多少千克)
3、按照行业规定:白酒的度数是指气温在20℃时,100ml酒中所含酒精的毫升数。请你根据行业规定计算白酒厂生产的每瓶“500ml 45°”的鲁源白酒的密度和质量分别是多少?(粗略认为白酒由纯水和酒精混合而成,不考虑混合时的体积变化)
