7.2.2 用坐标表示平移同步练习(含答案)
文档属性
| 名称 | 7.2.2 用坐标表示平移同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 957.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 13:24:04 | ||
图片预览



文档简介
人教版七年级数学下册7.2.2用坐标表示平移同步练习
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020秋?会宁县期末)线段CD是由线段AB平移得到的,点A(3,﹣1)的对应点C的坐标是(﹣2,5),则点B(0,4)的对应点D的坐标是( )
A.(5,﹣7) B.(4,3) C.(﹣5,10) D.(﹣3,7)
2.(2020秋?丹东期末)将三角形三个顶点的横坐标都减2,纵坐标不变,则所得三角形与原三角形的关系是( )
A.将原图向左平移两个单位
B.关于原点对称
C.将原图向右平移两个单位
D.关于y轴对称
3.(2020春?越秀区校级期中)在平面直角坐标系中,已知线段MN的两个端点的坐标分别是M(﹣5,2)、N(1,﹣4),将线段MN向上移动3个单位,向左移动2个单位平移后,点M,N的对应坐标为( )
A.(﹣5,1),(0,﹣5) B.(﹣4,2),(1,﹣3)
C.(﹣7,5),(﹣1,﹣1) D.(﹣5,0),(1,﹣5)
4.(2020秋?西华县期中)如图,将一颗小星星放置在平面直角坐标系中第二象限内的甲位置,先将它绕原点O旋转180°到乙位置,再将它向上平移2个单位长到丙位置,则小星星顶点A在丙位置中的对应点A'的坐标为( )
A.(﹣3,1) B.(1,3) C.(3,1) D.(3,﹣1)
5.(2020秋?烈山区期中)点P(﹣1,﹣3)向右平移3个单位,再向上平移5个单位,则所得到的点的坐标为( )
A.(﹣4,2) B.(2,2) C.(﹣4,﹣8) D.(2,﹣8)
6.(2020?温江区校级自主招生)在平面直角坐标系中,把点P(﹣4,2)先向左平移1个单位长度,再向上平移2个单位长度,得到的点的坐标是( )
A.(﹣5,4) B.(﹣5,0) C.(﹣3,4) D.(﹣3,0)
7.(2020秋?江州区期中)将点P(﹣2,6),先向右平移4个单位,再向下平移4个单位,则平移后得到点的坐标为( )
A.(2,2) B.(﹣2,﹣2) C.(﹣6,2) D.(﹣6,10)
8.(2020秋?岑溪市期中)在平面直角坐标系中,把点A(﹣2,2)平移到点A'(﹣5,2),其平移方法是( )
A.向上平移3个单位 B.向下平移3个单位
C.向左平移3个单位 D.向右平移3个单位
9.(2020秋?武侯区校级期中)在平面直角坐标系中,将点A(x,y)向左平移3个单位长度,再向上平移5个单位长度后与点B(﹣3,2)重合,则点A的坐标是( )
A.(2,5) B.(0,﹣3) C.(﹣2,5) D.(5,﹣3)
10.(2020秋?河南期中)在平面直角坐标系中,将△ABC各点的纵坐标保持不变,横坐标都减去3,则所得图形与原图形的关系:将原图形( )
A.向上平移3个单位长度 B.向下平移3个单位长度
C.向左平移3个单位长度 D.向右平移3个单位长度
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020秋?香坊区期末)将点P(﹣3,1)向上平移2个单位长度得到点Q,则点Q的坐标为 .
12.(2020秋?绿园区期末)将一点A(1,2)向右平移2个单位得到一个对应点A′,则点A′的坐标是 .
13.(2020秋?道里区期末)已知点A(3,2),将点A先向左平移4个单位长度,再向上平移5个单位长度得到点B,则B的坐标为 .
14.(2020秋?禅城区期末)如果将点A(﹣3,﹣2)向右移2个单位长度再向上平移3个单位长度单位得到点A1,那么点A1的坐标是 .
15.(2020春?江汉区月考)已知在平面直角坐标系中,线段AB的两个端点坐标分别为A(2,5),B(6,﹣2),点P(m,n)为线段AB上一点,若平移AB使其两个端点都落在坐标轴上,则平移后点P的坐标为 .
16.(2020秋?朝阳区校级月考)如图,点A、B的坐标分别为(0,2)、(3,0).若将线段AB平移至A1B1,则a2+b2的值为 .
17.(2020秋?武侯区校级期中)已知A(a﹣5,2b﹣1)在y轴上,B(3a+2,b+3)在x轴上,则C(a,b)向左平移2个单位长度再向上平移2个单位长度后的坐标为 .
18.(2020秋?田林县期中)在平面直角坐标系中,线段AB两个端点A(1,2),B(7,5).将线段AB平移后,点A的新坐标为(﹣6,﹣3),则点B的新坐标为 .
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020秋?松北区期末)按要求画图及填空:
在由边长为1个单位长度的小正方形组成的网格中建立如图所示平面直角坐标系,原点O及△ABC的顶点都在格点上.
(1)点A的坐标为 ;
(2)将△ABC先向下平移2个单位长度,再向右平移5个单位长度得到△A1B1C1,画出△A1B1C1.
(3)△A1B1C1的面积为 .
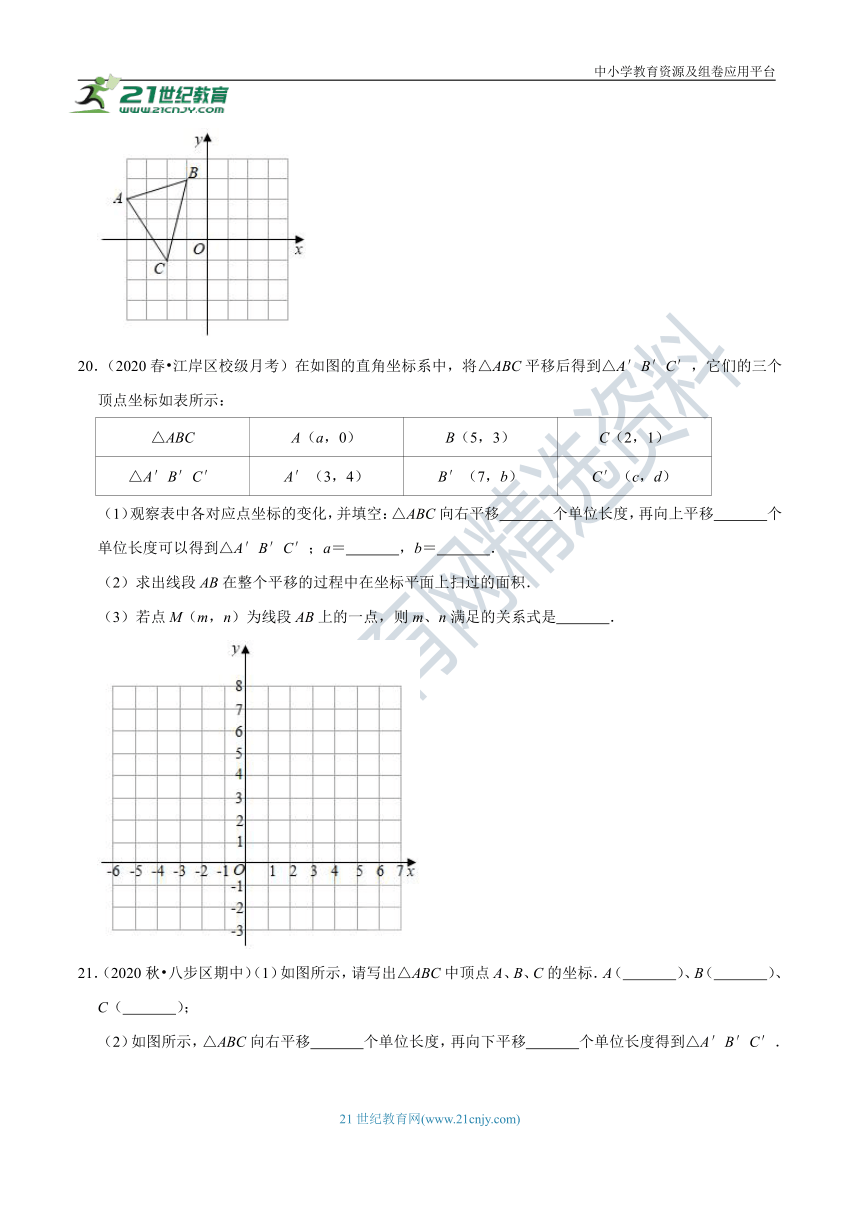
20.(2020春?江岸区校级月考)在如图的直角坐标系中,将△ABC平移后得到△A′B′C′,它们的三个顶点坐标如表所示:
△ABC
A(a,0)
B(5,3)
C(2,1)
△A′B′C′
A′(3,4)
B′(7,b)
C′(c,d)
(1)观察表中各对应点坐标的变化,并填空:△ABC向右平移 个单位长度,再向上平移 个单位长度可以得到△A′B′C′;a= ,b= .
(2)求出线段AB在整个平移的过程中在坐标平面上扫过的面积.
(3)若点M(m,n)为线段AB上的一点,则m、n满足的关系式是 .
21.(2020秋?八步区期中)(1)如图所示,请写出△ABC中顶点A、B、C的坐标.A( )、B( )、C( );
(2)如图所示,△ABC向右平移 个单位长度,再向下平移 个单位长度得到△A′B′C′.
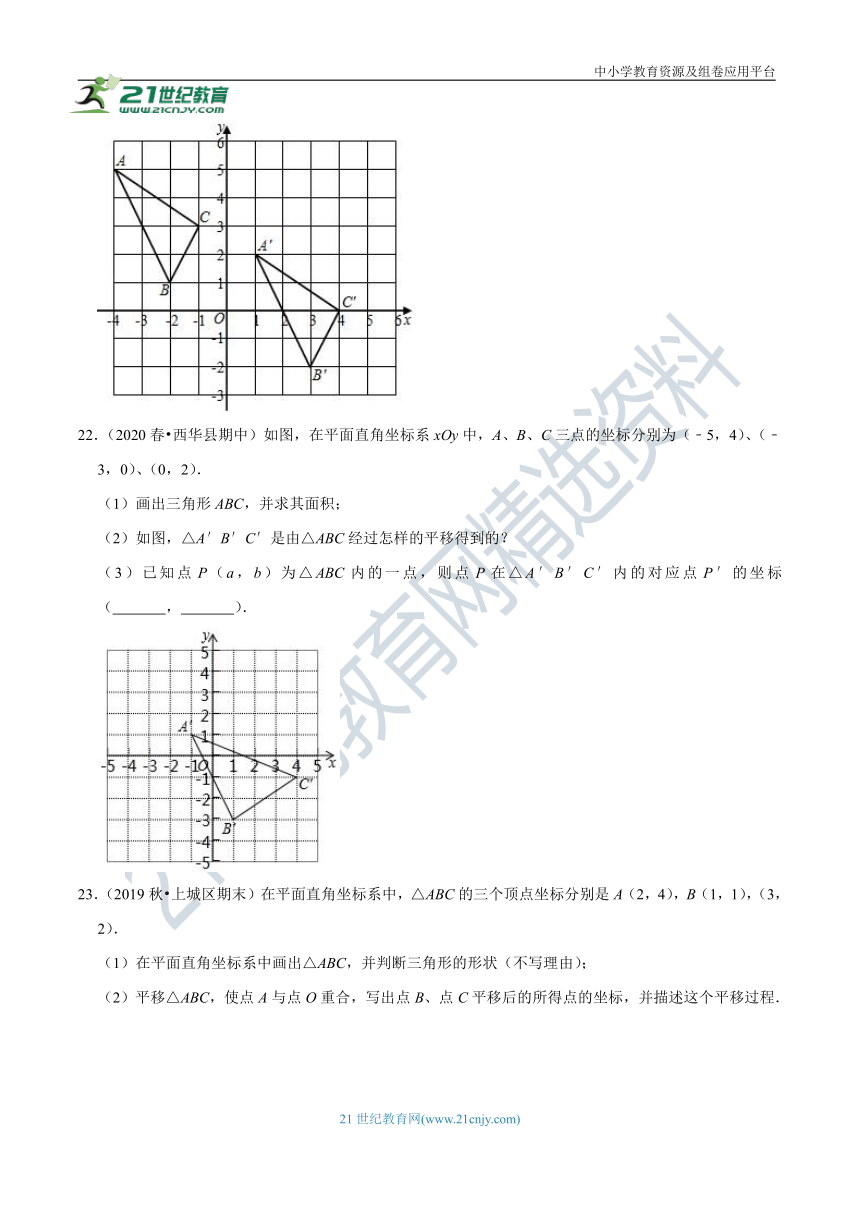
22.(2020春?西华县期中)如图,在平面直角坐标系xOy中,A、B、C三点的坐标分别为(﹣5,4)、(﹣3,0)、(0,2).
(1)画出三角形ABC,并求其面积;
(2)如图,△A′B′C′是由△ABC经过怎样的平移得到的?
(3)已知点P(a,b)为△ABC内的一点,则点P在△A′B′C′内的对应点P′的坐标( , ).
23.(2019秋?上城区期末)在平面直角坐标系中,△ABC的三个顶点坐标分别是A(2,4),B(1,1),(3,2).
(1)在平面直角坐标系中画出△ABC,并判断三角形的形状(不写理由);
(2)平移△ABC,使点A与点O重合,写出点B、点C平移后的所得点的坐标,并描述这个平移过程.
24.(2020春?石泉县期末)如图,三角形A′B'C'是由三角形ABC平移得到的.
(1)若点P(a,b)是三角形ABC内部一点,求平移后三角形A′B′C'内的对应点P′的坐标
(2)画出将三角形ABC向左平移4个单位,再向下平移1个单位得到的三角形A1B1C1.
答案
一、选择题
1.C.2.A.3.C.4.C.5.B.6.A.7.A.8.C.9.B.10.C.
二、填空题
11.(﹣3,3).
12.(3,2).
13.(﹣1,7).
14.(﹣1,1).
15.(m﹣2,n+2)或(m﹣6,n﹣5).
16.5.
17.(3,﹣1).
18.(0,0).
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.【解析】(1)如图所示:点A的坐标为(﹣4,2);
故答案为:(﹣4,2);
(2)如图所示:△A1B1C1,即为所求;
(3)△A1B1C1的面积为:3×4-12×1×3-12×2×3-12×1×4=5.5.
故答案为:5.5.
20.【解析】(1)∵A(a,0),A′(3,4),
∴△ABC向上平移4个单位后得到△A′B′C′,
∵B(5,3),B′(7,b),
∴△ABC向右平移2个单位后得到△A′B′C′,
∴a=1,b=3+4=7,
故答案为:2;4;1;7;
(2)线段AB在整个平移的过程中在坐标平面上扫过的面积:2×3+4×4=22;
(3)设AB所在直线解析式为y=kx+b,
∵A(1,0),B(5,3),
∴k+b=05k+b=3,
解得:k=34b=-34,
∴AB所在直线解析式为y=34x-34,
∵点M(m,n)为线段AB上的一点,
∴n=34m-34,
即:3m﹣4n=3,
故答案为:3m﹣4n=3.
21.【解析】(1)由图知,A(﹣4,5)、B(﹣2,1)、C(﹣1,3),
故答案为:﹣4,5;﹣2,1;﹣1,3.
(2)△ABC向右平移5个单位长度,再向下平移3个单位长度得到△A′B′C′,
故答案为:5,3.
22.【解析】(1)如图,△ABC即为所求.
S△ABC=4×5-12×2×4-12×2×5-12×2×3=8;
(2)先向右平移4个单位,再向下平移3个单位.
(3)由题意P′(a+4,b﹣3).
故答案为:a+4,b﹣3.
23.【解析】(1)如图,△ABC即为所求,△ABC 等腰直角三角形.
(2)平移后的△OB′C′即为所求,B′(﹣1,﹣3),C′(1,﹣2),△ABC向下平移4个单位,向左平移2个单位得到△OB′C′.
24.【解析】(1)由题意三角形A′B'C'是由三角形ABC向左平移5个单位,向上平移4个单位得到的,
∴点P′的坐标为(a﹣5,b+4);
(2)如图所示,
△A1B1C1即为所求.
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,试题共24题,选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020秋?会宁县期末)线段CD是由线段AB平移得到的,点A(3,﹣1)的对应点C的坐标是(﹣2,5),则点B(0,4)的对应点D的坐标是( )
A.(5,﹣7) B.(4,3) C.(﹣5,10) D.(﹣3,7)
2.(2020秋?丹东期末)将三角形三个顶点的横坐标都减2,纵坐标不变,则所得三角形与原三角形的关系是( )
A.将原图向左平移两个单位
B.关于原点对称
C.将原图向右平移两个单位
D.关于y轴对称
3.(2020春?越秀区校级期中)在平面直角坐标系中,已知线段MN的两个端点的坐标分别是M(﹣5,2)、N(1,﹣4),将线段MN向上移动3个单位,向左移动2个单位平移后,点M,N的对应坐标为( )
A.(﹣5,1),(0,﹣5) B.(﹣4,2),(1,﹣3)
C.(﹣7,5),(﹣1,﹣1) D.(﹣5,0),(1,﹣5)
4.(2020秋?西华县期中)如图,将一颗小星星放置在平面直角坐标系中第二象限内的甲位置,先将它绕原点O旋转180°到乙位置,再将它向上平移2个单位长到丙位置,则小星星顶点A在丙位置中的对应点A'的坐标为( )
A.(﹣3,1) B.(1,3) C.(3,1) D.(3,﹣1)
5.(2020秋?烈山区期中)点P(﹣1,﹣3)向右平移3个单位,再向上平移5个单位,则所得到的点的坐标为( )
A.(﹣4,2) B.(2,2) C.(﹣4,﹣8) D.(2,﹣8)
6.(2020?温江区校级自主招生)在平面直角坐标系中,把点P(﹣4,2)先向左平移1个单位长度,再向上平移2个单位长度,得到的点的坐标是( )
A.(﹣5,4) B.(﹣5,0) C.(﹣3,4) D.(﹣3,0)
7.(2020秋?江州区期中)将点P(﹣2,6),先向右平移4个单位,再向下平移4个单位,则平移后得到点的坐标为( )
A.(2,2) B.(﹣2,﹣2) C.(﹣6,2) D.(﹣6,10)
8.(2020秋?岑溪市期中)在平面直角坐标系中,把点A(﹣2,2)平移到点A'(﹣5,2),其平移方法是( )
A.向上平移3个单位 B.向下平移3个单位
C.向左平移3个单位 D.向右平移3个单位
9.(2020秋?武侯区校级期中)在平面直角坐标系中,将点A(x,y)向左平移3个单位长度,再向上平移5个单位长度后与点B(﹣3,2)重合,则点A的坐标是( )
A.(2,5) B.(0,﹣3) C.(﹣2,5) D.(5,﹣3)
10.(2020秋?河南期中)在平面直角坐标系中,将△ABC各点的纵坐标保持不变,横坐标都减去3,则所得图形与原图形的关系:将原图形( )
A.向上平移3个单位长度 B.向下平移3个单位长度
C.向左平移3个单位长度 D.向右平移3个单位长度
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020秋?香坊区期末)将点P(﹣3,1)向上平移2个单位长度得到点Q,则点Q的坐标为 .
12.(2020秋?绿园区期末)将一点A(1,2)向右平移2个单位得到一个对应点A′,则点A′的坐标是 .
13.(2020秋?道里区期末)已知点A(3,2),将点A先向左平移4个单位长度,再向上平移5个单位长度得到点B,则B的坐标为 .
14.(2020秋?禅城区期末)如果将点A(﹣3,﹣2)向右移2个单位长度再向上平移3个单位长度单位得到点A1,那么点A1的坐标是 .
15.(2020春?江汉区月考)已知在平面直角坐标系中,线段AB的两个端点坐标分别为A(2,5),B(6,﹣2),点P(m,n)为线段AB上一点,若平移AB使其两个端点都落在坐标轴上,则平移后点P的坐标为 .
16.(2020秋?朝阳区校级月考)如图,点A、B的坐标分别为(0,2)、(3,0).若将线段AB平移至A1B1,则a2+b2的值为 .
17.(2020秋?武侯区校级期中)已知A(a﹣5,2b﹣1)在y轴上,B(3a+2,b+3)在x轴上,则C(a,b)向左平移2个单位长度再向上平移2个单位长度后的坐标为 .
18.(2020秋?田林县期中)在平面直角坐标系中,线段AB两个端点A(1,2),B(7,5).将线段AB平移后,点A的新坐标为(﹣6,﹣3),则点B的新坐标为 .
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020秋?松北区期末)按要求画图及填空:
在由边长为1个单位长度的小正方形组成的网格中建立如图所示平面直角坐标系,原点O及△ABC的顶点都在格点上.
(1)点A的坐标为 ;
(2)将△ABC先向下平移2个单位长度,再向右平移5个单位长度得到△A1B1C1,画出△A1B1C1.
(3)△A1B1C1的面积为 .
20.(2020春?江岸区校级月考)在如图的直角坐标系中,将△ABC平移后得到△A′B′C′,它们的三个顶点坐标如表所示:
△ABC
A(a,0)
B(5,3)
C(2,1)
△A′B′C′
A′(3,4)
B′(7,b)
C′(c,d)
(1)观察表中各对应点坐标的变化,并填空:△ABC向右平移 个单位长度,再向上平移 个单位长度可以得到△A′B′C′;a= ,b= .
(2)求出线段AB在整个平移的过程中在坐标平面上扫过的面积.
(3)若点M(m,n)为线段AB上的一点,则m、n满足的关系式是 .
21.(2020秋?八步区期中)(1)如图所示,请写出△ABC中顶点A、B、C的坐标.A( )、B( )、C( );
(2)如图所示,△ABC向右平移 个单位长度,再向下平移 个单位长度得到△A′B′C′.
22.(2020春?西华县期中)如图,在平面直角坐标系xOy中,A、B、C三点的坐标分别为(﹣5,4)、(﹣3,0)、(0,2).
(1)画出三角形ABC,并求其面积;
(2)如图,△A′B′C′是由△ABC经过怎样的平移得到的?
(3)已知点P(a,b)为△ABC内的一点,则点P在△A′B′C′内的对应点P′的坐标( , ).
23.(2019秋?上城区期末)在平面直角坐标系中,△ABC的三个顶点坐标分别是A(2,4),B(1,1),(3,2).
(1)在平面直角坐标系中画出△ABC,并判断三角形的形状(不写理由);
(2)平移△ABC,使点A与点O重合,写出点B、点C平移后的所得点的坐标,并描述这个平移过程.
24.(2020春?石泉县期末)如图,三角形A′B'C'是由三角形ABC平移得到的.
(1)若点P(a,b)是三角形ABC内部一点,求平移后三角形A′B′C'内的对应点P′的坐标
(2)画出将三角形ABC向左平移4个单位,再向下平移1个单位得到的三角形A1B1C1.
答案
一、选择题
1.C.2.A.3.C.4.C.5.B.6.A.7.A.8.C.9.B.10.C.
二、填空题
11.(﹣3,3).
12.(3,2).
13.(﹣1,7).
14.(﹣1,1).
15.(m﹣2,n+2)或(m﹣6,n﹣5).
16.5.
17.(3,﹣1).
18.(0,0).
三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)
19.【解析】(1)如图所示:点A的坐标为(﹣4,2);
故答案为:(﹣4,2);
(2)如图所示:△A1B1C1,即为所求;
(3)△A1B1C1的面积为:3×4-12×1×3-12×2×3-12×1×4=5.5.
故答案为:5.5.
20.【解析】(1)∵A(a,0),A′(3,4),
∴△ABC向上平移4个单位后得到△A′B′C′,
∵B(5,3),B′(7,b),
∴△ABC向右平移2个单位后得到△A′B′C′,
∴a=1,b=3+4=7,
故答案为:2;4;1;7;
(2)线段AB在整个平移的过程中在坐标平面上扫过的面积:2×3+4×4=22;
(3)设AB所在直线解析式为y=kx+b,
∵A(1,0),B(5,3),
∴k+b=05k+b=3,
解得:k=34b=-34,
∴AB所在直线解析式为y=34x-34,
∵点M(m,n)为线段AB上的一点,
∴n=34m-34,
即:3m﹣4n=3,
故答案为:3m﹣4n=3.
21.【解析】(1)由图知,A(﹣4,5)、B(﹣2,1)、C(﹣1,3),
故答案为:﹣4,5;﹣2,1;﹣1,3.
(2)△ABC向右平移5个单位长度,再向下平移3个单位长度得到△A′B′C′,
故答案为:5,3.
22.【解析】(1)如图,△ABC即为所求.
S△ABC=4×5-12×2×4-12×2×5-12×2×3=8;
(2)先向右平移4个单位,再向下平移3个单位.
(3)由题意P′(a+4,b﹣3).
故答案为:a+4,b﹣3.
23.【解析】(1)如图,△ABC即为所求,△ABC 等腰直角三角形.
(2)平移后的△OB′C′即为所求,B′(﹣1,﹣3),C′(1,﹣2),△ABC向下平移4个单位,向左平移2个单位得到△OB′C′.
24.【解析】(1)由题意三角形A′B'C'是由三角形ABC向左平移5个单位,向上平移4个单位得到的,
∴点P′的坐标为(a﹣5,b+4);
(2)如图所示,
△A1B1C1即为所求.
