上海市闵行区2020-2021学年九年级(上)期末数学试卷(一模)(word版含解析)
文档属性
| 名称 | 上海市闵行区2020-2021学年九年级(上)期末数学试卷(一模)(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 329.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 10:44:15 | ||
图片预览



文档简介
2020-2021学年上海市闵行区九年级(上)期末数学试卷(一模)
一、选择题(本大共6题,每题4分,满分24分)
1.下列函数中,是二次函数的是( )
A.y=﹣﹣3x B.y=﹣(x﹣1)2+x2
C.y=11x2+29x D.y=ax2+bx+c
2.已知在Rt△ABC中,∠C=90°,∠B=β,AB=5,那么AC的长为( )
A.5cosβ B.5sinβ C. D.
3.如图,在平面直角坐标系xOy中,二次函数y=ax2+bx+c图象经过点O(0,0),那么根据图象,下列判断正确的是( )
A.a<0 B.b>0 C.ab>0 D.c=0
4.以下说法错误的是( )
A.如果k=,那么=
B.如果=﹣2,那么||=2||
C.如果=(为非零向量),那么∥
D.如果是与非向量同方向的单位向量,那么=||.
5.已知⊙A与⊙B的半径分别是6和8,圆心距AB=2,那么⊙A与⊙B的位置关系是( )
A.相交 B.内切 C.外切 D.内含
6.古希腊艺术家发现当人的头顶至肚脐的长度(上半身的长度)与肚脐至足底的长度(下半身的长度)的比值为“黄金分割数”时,人体的身材是最优美的.一位女士身高为154cm,她上半身的长度为62cm,为了使自己的身材显得更为优美,计划选择一双合适的高跟鞋,使自己的下半身长度增加.你认为选择鞋跟高为多少厘米的高跟鞋最佳?( )
A.4cm B.6cm C.8cm D.10cm
二、填空题(本大题共12题,每题4分,满分48分)
7.如果2a=3b(b≠0),那么= .
8.化简:(﹣3+)+= .
9.抛物线y=﹣x2﹣3x在对称轴的右侧部分是 的(填“上升”或“下降”).
10.将抛物线y=x2+2x向下平移1个单位,那么所得抛物线与y轴的交点的坐标为 .
11.已知两个相似三角形的相似比为4:9,那么这两个三角形的周长之比为 .
12.在△ABC中,点D、E分别在边AB、AC上,且DE∥BC,如果,那么= .
13.在直角坐标平面内有一点A(12,5),点A与原点O的连线与x轴的正半轴的夹角为θ,那么cosθ= .
14.如果港口A的南偏东52°方向有一座小岛B,那么从小岛B观察港口A的方向是 .
15.正六边形的边心距与半径的比值为 .
16.如图,在△ABC中,AB=2AC,点D在边AB上,且∠ACD=∠B,那么= .
17.如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,点P在边AC上,⊙P的半径为1.如果⊙P与边BC和边AB都没有公共点,那么线段PC长的取值范围是 .
18.如图,在Rt△ABC中,∠ACB=90°,AB=3,tanB=.将△ABC绕着点A顺时针旋转后,点B恰好落在射线CA上的点D处,点C落在点E处,射线DE与边AB相交于点F,那么BF= .
三、解答题(本大题共7题,满分78分)
19.(10分)计算:2cos60°﹣cot30°+.
20.(10分)如图,在平行四边形ABCD中,对角线AC、BD相交于点O.E为OC的中点,联结BE并延长,交边CD于点F.设=,=.
(1)填空:向量= ;
(2)填空:向量= ,并在图中画出向量在向量和方向上的分向量.
(注:本体结果用含向量、的式子表示,画图不要求写作法,但要指出所作图中表示结论的向量)
21.(10分)如图,⊙O是△BC的外接圆,AB长为4,AB=AC,联结CO并延长,交边AB于点D,交AB于点E,且E为弧AB的中点.求:
(1)边BC的长;
(2)⊙O的半径.
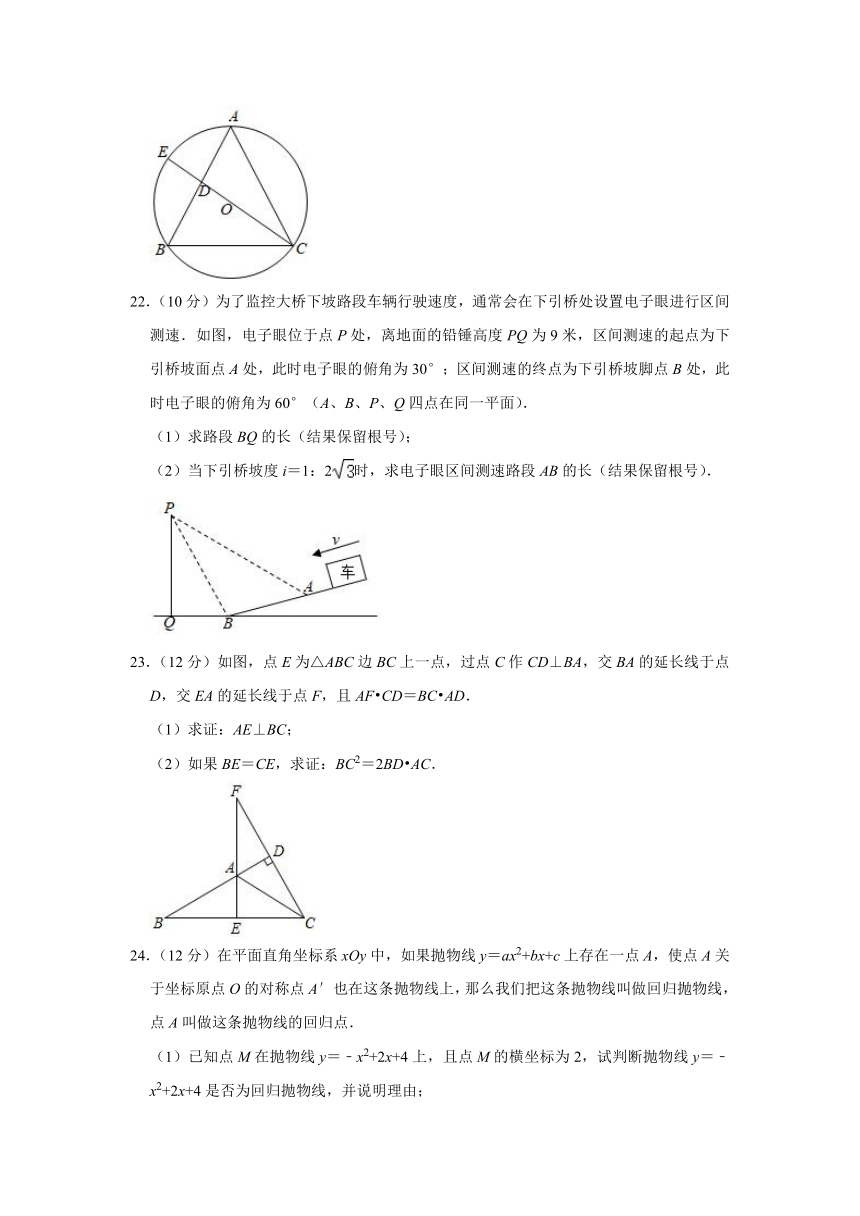
22.(10分)为了监控大桥下坡路段车辆行驶速度,通常会在下引桥处设置电子眼进行区间测速.如图,电子眼位于点P处,离地面的铅锤高度PQ为9米,区间测速的起点为下引桥坡面点A处,此时电子眼的俯角为30°;区间测速的终点为下引桥坡脚点B处,此时电子眼的俯角为60°(A、B、P、Q四点在同一平面).
(1)求路段BQ的长(结果保留根号);
(2)当下引桥坡度i=1:2时,求电子眼区间测速路段AB的长(结果保留根号).
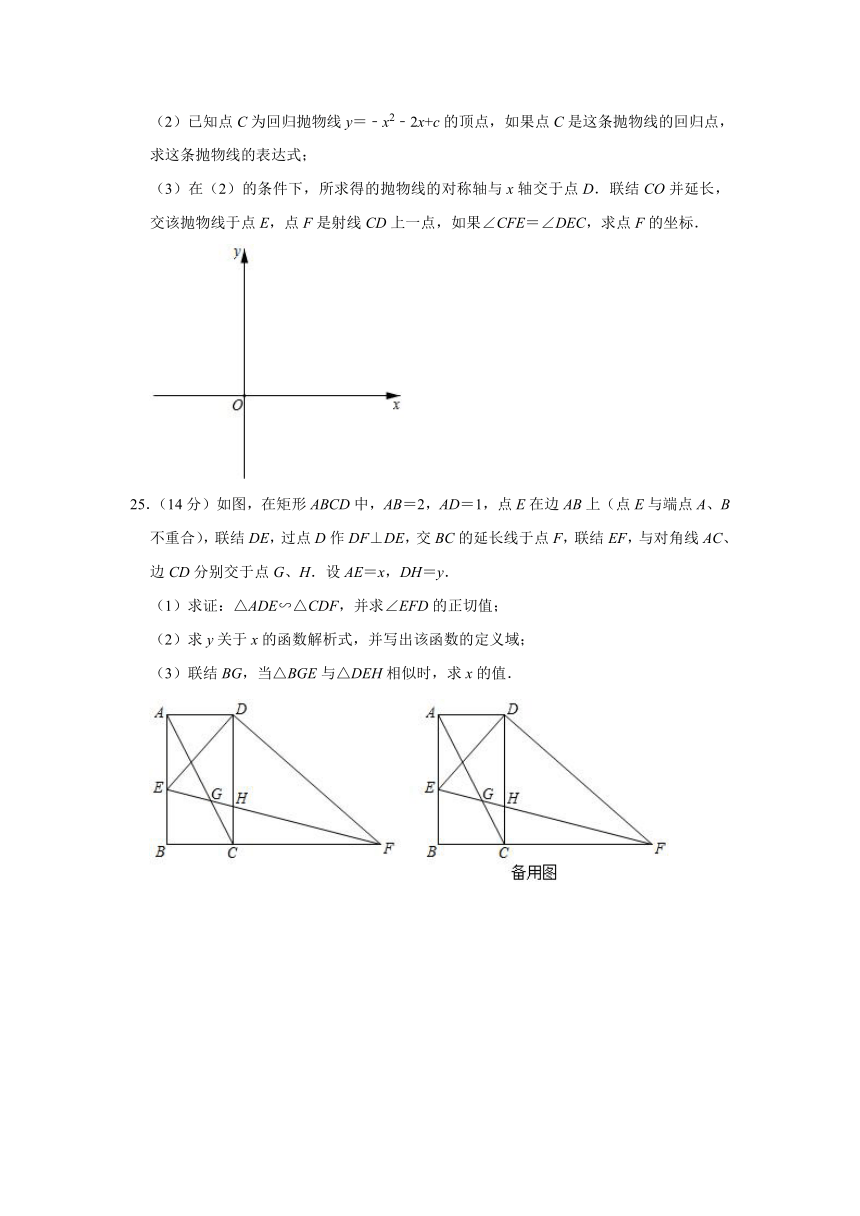
23.(12分)如图,点E为△ABC边BC上一点,过点C作CD⊥BA,交BA的延长线于点D,交EA的延长线于点F,且AF?CD=BC?AD.
(1)求证:AE⊥BC;
(2)如果BE=CE,求证:BC2=2BD?AC.
24.(12分)在平面直角坐标系xOy中,如果抛物线y=ax2+bx+c上存在一点A,使点A关于坐标原点O的对称点A′也在这条抛物线上,那么我们把这条抛物线叫做回归抛物线,点A叫做这条抛物线的回归点.
(1)已知点M在抛物线y=﹣x2+2x+4上,且点M的横坐标为2,试判断抛物线y=﹣x2+2x+4是否为回归抛物线,并说明理由;
(2)已知点C为回归抛物线y=﹣x2﹣2x+c的顶点,如果点C是这条抛物线的回归点,求这条抛物线的表达式;
(3)在(2)的条件下,所求得的抛物线的对称轴与x轴交于点D.联结CO并延长,交该抛物线于点E,点F是射线CD上一点,如果∠CFE=∠DEC,求点F的坐标.
25.(14分)如图,在矩形ABCD中,AB=2,AD=1,点E在边AB上(点E与端点A、B不重合),联结DE,过点D作DF⊥DE,交BC的延长线于点F,联结EF,与对角线AC、边CD分别交于点G、H.设AE=x,DH=y.
(1)求证:△ADE∽△CDF,并求∠EFD的正切值;
(2)求y关于x的函数解析式,并写出该函数的定义域;
(3)联结BG,当△BGE与△DEH相似时,求x的值.
2020-2021学年上海市闵行区九年级(上)期末数学试卷(一模)
参考答案与试题解析
一、选择题(本大共6题,每题4分,满分24分)
1.下列函数中,是二次函数的是( )
A.y=﹣﹣3x B.y=﹣(x﹣1)2+x2
C.y=11x2+29x D.y=ax2+bx+c
【分析】利用二次函数定义进行分析即可.
【解答】解:A、含有分式,不是二次函数,故此选项不合题意;
B、y=﹣(x﹣1)2+x2=2x﹣1,不是二次函数,故此选项不合题意;
C、是二次函数,故此选项符合题意;
D、当a=0时,不是二次函数,故此选项不合题意;
故选:C.
【点评】此题主要考查了二次函数,关键是掌握判断函数是否是二次函数,首先是要看它的右边是否为整式,若是整式且仍能化简的要先将其化简,然后再根据二次函数的定义作出判断,要抓住二次项系数不为0这个关键条件.
2.已知在Rt△ABC中,∠C=90°,∠B=β,AB=5,那么AC的长为( )
A.5cosβ B.5sinβ C. D.
【分析】根据锐角三角函数的定义即可得出答案.
【解答】解:在Rt△ABC中,∵∠C=90°,∠B=β,AB=5,
∴sinB=sinβ=,
∴AC=AB?sinβ=5sinβ,
故选:B.
【点评】本题考查锐角三角函数的定义,理解锐角三角函数的意义是解决问题的关键.
3.如图,在平面直角坐标系xOy中,二次函数y=ax2+bx+c图象经过点O(0,0),那么根据图象,下列判断正确的是( )
A.a<0 B.b>0 C.ab>0 D.c=0
【分析】根据抛物线的开口方向,对称轴以及与y轴的交点进行判断即可.
【解答】解:∵抛物线开口向上,
∴a>0,故A错误;
∵﹣>0,a>0,
∴b<0,故B错误;
∵a>0,b<0,
∴ab<0,故C错误;
∵图象经过点O(0,0),
∴c=0,故D正确;
故选:D.
【点评】本题考查了二次函数的图象与系数的关系,对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向.当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c).抛物线与x轴交点个数由△决定:△=b2﹣4ac>0时,抛物线与x轴有2个交点;△=b2﹣4ac=0时,抛物线与x轴有1个交点;△=b2﹣4ac<0时,抛物线与x轴没有交点.
4.以下说法错误的是( )
A.如果k=,那么=
B.如果=﹣2,那么||=2||
C.如果=(为非零向量),那么∥
D.如果是与非向量同方向的单位向量,那么=||.
【分析】根据共线向量的定义,零向量的意义进行判断.
【解答】解:A、如果k=,那么k=0,故本选项符合题意.
B、如果=﹣2,那么||=2||,故本选项不符合题意.
C、如果=(为非零向量),那么与方向相同,则∥,故本选项不符合题意.
D、如果是与非向量同方向的单位向量,那么=||,故本选项不符合题意.
故选:A.
【点评】本题主要考查了平面向量,注意:平面向量既有大小,又有方向.
5.已知⊙A与⊙B的半径分别是6和8,圆心距AB=2,那么⊙A与⊙B的位置关系是( )
A.相交 B.内切 C.外切 D.内含
【分析】求出两圆半径的和与差,再与圆心距比较大小,确定两圆位置关系;设两圆的半径分别为R和r,且R≥r,圆心距为d:外离,则d>R+r;外切,则d=R+r;相交,则R﹣r<d<R+r;内切,则d=R﹣r;内含,则d<R﹣r.
【解答】解:因为8﹣6=2,圆心距AB=2,
所以d=R﹣r,
所以两圆内切.
故选:B.
【点评】考查了圆与圆的位置关系,本题利用了两圆内切,则d=R﹣r.
6.古希腊艺术家发现当人的头顶至肚脐的长度(上半身的长度)与肚脐至足底的长度(下半身的长度)的比值为“黄金分割数”时,人体的身材是最优美的.一位女士身高为154cm,她上半身的长度为62cm,为了使自己的身材显得更为优美,计划选择一双合适的高跟鞋,使自己的下半身长度增加.你认为选择鞋跟高为多少厘米的高跟鞋最佳?( )
A.4cm B.6cm C.8cm D.10cm
【分析】她下半身的长度为92cm,设鞋跟高为x厘米时,她身材显得更为优美,利用黄金分割的定义得到≈0.618,然后解方程即可.
【解答】解:∵一位女士身高为154cm,她上半身的长度为62cm,
∴她下半身的长度为92cm,
设鞋跟高为x厘米时,她身材显得更为优美,
根据题意得≈0.618,
解得x≈8.3(cm).
经检验x=8.3为原方程的解,
所以选择鞋跟高为8厘米的高跟鞋最佳.
故选:C.
【点评】本题考查了因式分解的应用:利用因式分解解决求值问题.利用因式分解解决证明问题.利用因式分解简化计算问题.也考查了黄金分割.
二、填空题(本大题共12题,每题4分,满分48分)
7.如果2a=3b(b≠0),那么= .
【分析】根据比例的性质直接解答即可.
【解答】解:∵2a=3b(b≠0),
∴=.
故答案为:.
【点评】此题考查了比例的性质,熟练掌握两内项之积等于两外项之积是解题的关键.
8.化简:(﹣3+)+= ﹣+ .
【分析】先利用乘法结合律去括号,然后计算加减法.
【解答】解:原式=﹣++=﹣+.
故答案是:﹣+.
【点评】本题主要考查了平面向量,实数的运算法则同样能应用于平面向量的计算之中.
9.抛物线y=﹣x2﹣3x在对称轴的右侧部分是 下降 的(填“上升”或“下降”).
【分析】根据抛物线解析式可求得其开口方向和对称轴,结合抛物线的增减性可得到答案.
【解答】解:∵y=﹣x2﹣3x,
∴抛物线开口向下,对称轴为直线x=﹣=﹣,
∴在y轴右侧,y随x增大而减小,
∴其图象在y轴右侧部分是下降,
故答案为:下降.
【点评】本题主要考查二次函数的增减性,掌握开口向下的二次函数在对称轴右侧y随x的增大而减小是解题的关键.
10.将抛物线y=x2+2x向下平移1个单位,那么所得抛物线与y轴的交点的坐标为 (0,﹣1) .
【分析】根据“左加右减、上加下减”的原则写出新抛物线解析式,然后将二次函数解析式转化为方程,通过解解方程求解.
【解答】解:由“左加右减、上加下减”的原则可知,把抛物线y=x2+2x=(x+1)2﹣1的图象向下平移1个单位,则平移后的抛物线的表达式为y=x2+2x=(x+1)2﹣2,
令x=0,则y=﹣1.
所以所得抛物线与y轴的交点的坐标为(0,﹣1).
故答案是:(0,﹣1).
【点评】本题考查的是二次函数的图象与几何变换,要求熟练掌握平移的规律:左加右减,上加下减.
11.已知两个相似三角形的相似比为4:9,那么这两个三角形的周长之比为 4:9 .
【分析】直接利用相似三角形的周长比等于相似比,进而得出答案.
【解答】解:∵两个相似三角形的相似比为4:9,
∴它们的周长比等于相似比,即:4:9.
故答案为4:9.
【点评】本题考查对相似三角形性质的理解.(1)相似三角形周长的比等于相似比.(2)相似三角形面积的比等于相似比的平方.(3)相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.
12.在△ABC中,点D、E分别在边AB、AC上,且DE∥BC,如果,那么= .
【分析】由DE∥BC证△ADE∽△ABC,得==,继而可得答案.
【解答】解:如图,
∵DE∥BC,
∴△ADE∽△ABC,
∴==,
∴=,
故答案为:.
【点评】本题主要考查相似三角形的判定与性质,解题的关键是掌握相似三角形的判定和性质.
13.在直角坐标平面内有一点A(12,5),点A与原点O的连线与x轴的正半轴的夹角为θ,那么cosθ= .
【分析】根据题意,作出合适的平面直角坐标系,然后作AB⊥x轴于点B,再根据点的A的坐标和勾股定理,可以得到OA的长,然后即可得到cosθ的值.
【解答】解:作AB⊥x轴于点B,如右图所示,
∵点A(12,5),
∴OB=12,AB=5,∠ABO=90°,
∴OA==13,
∴cos∠AOB=,
即cosθ=,
故答案为:.
【点评】本题考查解直角三角形、勾股定理、锐角三角函数,解答本题的关键是明确题意,利用数形结合的思想解答.
14.如果港口A的南偏东52°方向有一座小岛B,那么从小岛B观察港口A的方向是 北偏西52° .
【分析】根据方位角的概念,画图正确表示出方位角,即可求解.
【解答】解:如图,∵∠1=∠2=52°,
∴从小岛B观察港口A的方向是北偏西52°.
故答案为:北偏西52°.
【点评】此题主要考查了方向角,正确画出方位角,根据平行线的性质解答是解题关键.
15.正六边形的边心距与半径的比值为 .
【分析】设正六边形的半径与外接圆的半径相等,构建直角三角形利用勾股定理即可求出边心距.
【解答】解:设正六边形的半径是r,则外接圆的半径r,内切圆的半径是正六边形的边心距,因而是,则可知正六边形的边心距与半径的比值为.
【点评】正多边形的计算一般是通过中心作边的垂线,连接半径,把正多边形中的半径,边长,边心距,中心角之间的计算转化为解直角三角形.
16.如图,在△ABC中,AB=2AC,点D在边AB上,且∠ACD=∠B,那么= .
【分析】根据相似三角形面积的比等于相似比的平方即可得结论.
【解答】解:∵∠ACD=∠B,∠A=∠A,
∴△ACD∽△ABC,
∴=()2=()2=.
故答案为:.
【点评】本题考查了相似三角形的判定与性质,解决本题的关键是掌握相似三角形的判定与性质.
17.如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,点P在边AC上,⊙P的半径为1.如果⊙P与边BC和边AB都没有公共点,那么线段PC长的取值范围是 1<CP< .
【分析】根据勾股定理得到AC=4,当⊙P与AB相切时,设切点为D,如图,连接PD,则PD⊥AB,根据相似三角形的性质可得到结论.
【解答】解:在Rt△ABC中,∠ACB=90°,AB=5,BC=3,
∴AC=4,
当⊙P与AB相切时,设切点为D,如图,
连接PD,
则PD⊥AB,
∴∠C=∠ADP=90°,
∵∠A=∠A,
∴△ADP∽△ACB,
∴,
∴=,
∴PA=,
∴PC=AC﹣PA=,
∴线段PC长的取值范围是1<CP<,
故答案为:1<CP<.
【点评】本题考查了直线与圆的位置关系,相似三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.
18.如图,在Rt△ABC中,∠ACB=90°,AB=3,tanB=.将△ABC绕着点A顺时针旋转后,点B恰好落在射线CA上的点D处,点C落在点E处,射线DE与边AB相交于点F,那么BF= 3﹣ .
【分析】过点F作FG⊥AC于点G,由旋转的性质得出∠B=∠D,得出tan∠B=tan∠D=,由平行线的性质得出∠B=∠AFG,设AG=x,则FG=2x,则,求出AG=1,则可得出答案.
【解答】解:如图,过点F作FG⊥AC于点G,
∵将△ABC绕着点A顺时针旋转后,点B恰好落在射线CA上的点D处,
∴∠B=∠D,
∴tan∠B=tan∠D=,
∵∠ACB=∠FGA=90°,
∴BC∥FG,
∴∠B=∠AFG,
∴tan∠B=tan∠AFG=,
设AG=x,则FG=2x,
∴,
解得x=1,
∴AG=1,FG=2,
∴AF===,
∴BF=AB﹣AF=3﹣.
故答案为:3﹣.
【点评】本题考查了旋转的性质,直角三角形的性质,锐角三角函数的定义,勾股定理,熟练掌握旋转的性质是解题的关键.
三、解答题(本大题共7题,满分78分)
19.(10分)计算:2cos60°﹣cot30°+.
【分析】直接利用特殊角的三角函数值以及二次根式的性质化简得出答案.
【解答】解:原式=2×﹣+
=1﹣+
=1﹣+
=1﹣++1
=2.
【点评】此题主要考查了特殊角的三角函数值二次根式的混合运算,正确化简各数是解题关键.
20.(10分)如图,在平行四边形ABCD中,对角线AC、BD相交于点O.E为OC的中点,联结BE并延长,交边CD于点F.设=,=.
(1)填空:向量= ﹣ ;
(2)填空:向量= + ,并在图中画出向量在向量和方向上的分向量.
(注:本体结果用含向量、的式子表示,画图不要求写作法,但要指出所作图中表示结论的向量)
【分析】(1)利用三角形法则求出,再证明AE=AC即可解决问题.
(2)利用平行线分线段成比例定理,求出,再利用三角形法则即可解决问题.
【解答】解:(1)∵=+,=,=.
∴=﹣,
∵四边形ABCD是平行四边形,
∴OA=OC,
∵OE=EC,
∴AE=AC,
∴=﹣.
故答案为:﹣.
(2)∵CF∥AB,
∴CF:AB=EC:AE=1:3,
∴CF=BA,
∴=,
∴=+=+.
在向量和方向上的分向量分别为和.
故答案为:+.
【点评】本题考查作图﹣复杂作图,平四边形的性质,平面向量,三角形法则,平行四边形法则等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
21.(10分)如图,⊙O是△BC的外接圆,AB长为4,AB=AC,联结CO并延长,交边AB于点D,交AB于点E,且E为弧AB的中点.求:
(1)边BC的长;
(2)⊙O的半径.
【分析】(1)利用垂径定理的推论可判断CD垂直平分AB,所以CB=CA=4;
(2)连接OB,如图,先证明ABC为等边三角形得到∠A=60°,利用圆周角定理得到∠BOC=120°,则∠BOD=60°,然后利用含30度的直角三角形三边的关系求出OB即可.
【解答】解:(1)∵E点为的中点,CE为直径,
∴CE⊥AB,
∴AD=BD,
即CD垂直平分AB,
∴CB=CA=4;
(2)连接OB,如图,
∵AB=BC=AC,
∴△ABC为等边三角形,
∴∠A=60°,
∴∠BOC=2∠A=120°,
∴∠BOD=60°,
在Rt△BOD中,BD=AB=2,
∴OD=BD=,
∴OB=2OD=,
即⊙O的半径为.
【点评】本题考查了三角形的外接圆与外心:三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.也考查了圆周角定理.
22.(10分)为了监控大桥下坡路段车辆行驶速度,通常会在下引桥处设置电子眼进行区间测速.如图,电子眼位于点P处,离地面的铅锤高度PQ为9米,区间测速的起点为下引桥坡面点A处,此时电子眼的俯角为30°;区间测速的终点为下引桥坡脚点B处,此时电子眼的俯角为60°(A、B、P、Q四点在同一平面).
(1)求路段BQ的长(结果保留根号);
(2)当下引桥坡度i=1:2时,求电子眼区间测速路段AB的长(结果保留根号).
【分析】(1)根据 BQ=PQ?tan∠BPQ,求解即可.
(2)如图,过点A作AM⊥QB于M,AH⊥PQ于H.由题意,∠PAH=∠TPA=30°,设AM=a米,则BM=2a米,在Rt△APH中,根据tan∠PAH=,构建方程求出a,再利用勾股定理求出AB即可.
【解答】解:(1)由题意,∠PBQ=∠TPB=60°,
∵∠PQB=90°,
∴∠BPQ=30°,
∴BQ=PQ?tan30°=9×=3(米).
(2)如图,过点A作AM⊥QB于M,AH⊥PQ于H.
由题意,∠PAH=∠TPA=30°,
设AM=a米,则BM=2a米,
∵∠AHQ=∠HQM=∠AMQ=90°,
∴四边形AHQM是矩形,
∴AH=QM=(3+2a)米,QH=AM=a米,PH=PQ﹣HQ=(9﹣a)米,
在Rt△APH中,tan∠PAH=,
∴=,
解得a=2,
∴AM=2(米),BM=4(米),
∴AB===2(米).
【点评】本题考查解直角三角形的应用﹣仰角俯角问题,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
23.(12分)如图,点E为△ABC边BC上一点,过点C作CD⊥BA,交BA的延长线于点D,交EA的延长线于点F,且AF?CD=BC?AD.
(1)求证:AE⊥BC;
(2)如果BE=CE,求证:BC2=2BD?AC.
【分析】(1)通过证明△ADF∽△CDB,可得∠F=∠B,由余角的性质可求解;
(2)通过证明△ABE∽△CBD,可得,可得结论.
【解答】证明:(1)∵AF?CD=BC?AD,
∴,
又∵∠ADF=∠BDC,
∴△ADF∽△CDB,
∴∠F=∠B,
∵∠B+∠BCD=90°,
∴∠F+∠BCD=90°,
∴AE⊥BC;
(2)∵BE=CE,AE⊥BC,
∴AB=AC,
∵∠ABE=∠DBC,∠BDC=∠AEB=90°,
∴△ABE∽△CBD,
∴,
∴BC?BC=AB?BD,
∴BC2=2BD?AC.
【点评】本题考查了相似三角形的判定和性质,掌握相似三角形的判定定理是本题的关键.
24.(12分)在平面直角坐标系xOy中,如果抛物线y=ax2+bx+c上存在一点A,使点A关于坐标原点O的对称点A′也在这条抛物线上,那么我们把这条抛物线叫做回归抛物线,点A叫做这条抛物线的回归点.
(1)已知点M在抛物线y=﹣x2+2x+4上,且点M的横坐标为2,试判断抛物线y=﹣x2+2x+4是否为回归抛物线,并说明理由;
(2)已知点C为回归抛物线y=﹣x2﹣2x+c的顶点,如果点C是这条抛物线的回归点,求这条抛物线的表达式;
(3)在(2)的条件下,所求得的抛物线的对称轴与x轴交于点D.联结CO并延长,交该抛物线于点E,点F是射线CD上一点,如果∠CFE=∠DEC,求点F的坐标.
【分析】(1)先求出点M坐标,M'的坐标,代入解析式可求解;
(2)先求出点C坐标,C'的坐标,利用回归点的定义可求解;
(3)通过证明△CEF∽△CDE,可得,可求CF=10,即可求解.
【解答】解:(1)抛物线y=﹣x2+2x+4是回归抛物线,
理由如下:∵点M在抛物线y=﹣x2+2x+4上,
∴y=﹣4+4+4=4,
∴点M(2,4),
∴点M关于坐标原点O的对称点M'(﹣2,﹣4),
当x=﹣2时,y=﹣4﹣4+4=﹣4,
∴点M'在抛物线上,
∴抛物线y=﹣x2+2x+4是回归抛物线;
(2)∵点C为回归抛物线y=﹣x2﹣2x+c的顶点,
∴点C(﹣1,c+1),
∴点C关于原点O的对称点C'(1,﹣c﹣1),
∵点C是这条抛物线的回归点,
∴﹣c﹣1=﹣1﹣2+c,
∴c=1,
∴抛物线解析式为:y=﹣x2﹣2x+1;
(3)∵抛物线y=﹣x2﹣2x+1,
∴对称点为x=﹣1,
∴点D(﹣1,0),点C(﹣1,2),
∴直线CO解析式为y=﹣2x,
联立方程组,
∴,,
点E(1,﹣2),
在△CEF和△CDE中,∠CFE=∠CED,∠FCE=∠ECD,
∴△CEF∽△CDE,
∴,
∴CE2=CD?CF,
∴(﹣1﹣1)2+(2+2)2=2CF,
∴CF=10,
∴F(﹣1,﹣8).
【点评】本题是二次函数综合题,考查了二次函数的性质,相似三角形的判定和性质,理解新定义并运用是解题的关键.
25.(14分)如图,在矩形ABCD中,AB=2,AD=1,点E在边AB上(点E与端点A、B不重合),联结DE,过点D作DF⊥DE,交BC的延长线于点F,联结EF,与对角线AC、边CD分别交于点G、H.设AE=x,DH=y.
(1)求证:△ADE∽△CDF,并求∠EFD的正切值;
(2)求y关于x的函数解析式,并写出该函数的定义域;
(3)联结BG,当△BGE与△DEH相似时,求x的值.
【分析】(1)根据矩形的性质得到∠ADC=∠DCB=90°,根据余角的性质得到∠ADE=∠CDF,由相似三角形的判定定理即可得到结论;
(2)根据矩形的性质和相似三角形的判定和性质解答;
(3)根据相似三角形的性质分两种情况解答.
【解答】解:(1)∵∠ADE+∠CDE=90°,∠CDF+∠CDE=90°,
∴∠ADE=∠CDF,
在Rt△EAD与Rt△FCD中,
,
∴△FAD∽△FCD,
∴,
∴tan∠EFD=,
(2)由(1)可知FC=2EA=2x,
∵四边形ABCD是矩形,
∴AB∥CD,
∴△FCH∽△FBE,
∴,
∴,
可得:y=(0<x<2);
(3)BE=2﹣x,DH=y,DE=,EH=,
∴,
∴EG=,
∵∠BEG=∠DHE,
若△BEG∽△DHE,则有两种情况,
第一种:
∵∠EGB=∠HED,
∴,
∴,
即,
解得:x=,
第二种:
∵∠EGB=∠HDE,
∴,
∴,
即,
解得:x=1.5.
综上所述,x的值为或1.5.
【点评】本题考查了相似综合题,综合运用了相似三角形的判定和性质,求函数的解析式,矩形的性质等知识点,熟练掌握相似三角形的判定和性质是解题的关键.
一、选择题(本大共6题,每题4分,满分24分)
1.下列函数中,是二次函数的是( )
A.y=﹣﹣3x B.y=﹣(x﹣1)2+x2
C.y=11x2+29x D.y=ax2+bx+c
2.已知在Rt△ABC中,∠C=90°,∠B=β,AB=5,那么AC的长为( )
A.5cosβ B.5sinβ C. D.
3.如图,在平面直角坐标系xOy中,二次函数y=ax2+bx+c图象经过点O(0,0),那么根据图象,下列判断正确的是( )
A.a<0 B.b>0 C.ab>0 D.c=0
4.以下说法错误的是( )
A.如果k=,那么=
B.如果=﹣2,那么||=2||
C.如果=(为非零向量),那么∥
D.如果是与非向量同方向的单位向量,那么=||.
5.已知⊙A与⊙B的半径分别是6和8,圆心距AB=2,那么⊙A与⊙B的位置关系是( )
A.相交 B.内切 C.外切 D.内含
6.古希腊艺术家发现当人的头顶至肚脐的长度(上半身的长度)与肚脐至足底的长度(下半身的长度)的比值为“黄金分割数”时,人体的身材是最优美的.一位女士身高为154cm,她上半身的长度为62cm,为了使自己的身材显得更为优美,计划选择一双合适的高跟鞋,使自己的下半身长度增加.你认为选择鞋跟高为多少厘米的高跟鞋最佳?( )
A.4cm B.6cm C.8cm D.10cm
二、填空题(本大题共12题,每题4分,满分48分)
7.如果2a=3b(b≠0),那么= .
8.化简:(﹣3+)+= .
9.抛物线y=﹣x2﹣3x在对称轴的右侧部分是 的(填“上升”或“下降”).
10.将抛物线y=x2+2x向下平移1个单位,那么所得抛物线与y轴的交点的坐标为 .
11.已知两个相似三角形的相似比为4:9,那么这两个三角形的周长之比为 .
12.在△ABC中,点D、E分别在边AB、AC上,且DE∥BC,如果,那么= .
13.在直角坐标平面内有一点A(12,5),点A与原点O的连线与x轴的正半轴的夹角为θ,那么cosθ= .
14.如果港口A的南偏东52°方向有一座小岛B,那么从小岛B观察港口A的方向是 .
15.正六边形的边心距与半径的比值为 .
16.如图,在△ABC中,AB=2AC,点D在边AB上,且∠ACD=∠B,那么= .
17.如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,点P在边AC上,⊙P的半径为1.如果⊙P与边BC和边AB都没有公共点,那么线段PC长的取值范围是 .
18.如图,在Rt△ABC中,∠ACB=90°,AB=3,tanB=.将△ABC绕着点A顺时针旋转后,点B恰好落在射线CA上的点D处,点C落在点E处,射线DE与边AB相交于点F,那么BF= .
三、解答题(本大题共7题,满分78分)
19.(10分)计算:2cos60°﹣cot30°+.
20.(10分)如图,在平行四边形ABCD中,对角线AC、BD相交于点O.E为OC的中点,联结BE并延长,交边CD于点F.设=,=.
(1)填空:向量= ;
(2)填空:向量= ,并在图中画出向量在向量和方向上的分向量.
(注:本体结果用含向量、的式子表示,画图不要求写作法,但要指出所作图中表示结论的向量)
21.(10分)如图,⊙O是△BC的外接圆,AB长为4,AB=AC,联结CO并延长,交边AB于点D,交AB于点E,且E为弧AB的中点.求:
(1)边BC的长;
(2)⊙O的半径.
22.(10分)为了监控大桥下坡路段车辆行驶速度,通常会在下引桥处设置电子眼进行区间测速.如图,电子眼位于点P处,离地面的铅锤高度PQ为9米,区间测速的起点为下引桥坡面点A处,此时电子眼的俯角为30°;区间测速的终点为下引桥坡脚点B处,此时电子眼的俯角为60°(A、B、P、Q四点在同一平面).
(1)求路段BQ的长(结果保留根号);
(2)当下引桥坡度i=1:2时,求电子眼区间测速路段AB的长(结果保留根号).
23.(12分)如图,点E为△ABC边BC上一点,过点C作CD⊥BA,交BA的延长线于点D,交EA的延长线于点F,且AF?CD=BC?AD.
(1)求证:AE⊥BC;
(2)如果BE=CE,求证:BC2=2BD?AC.
24.(12分)在平面直角坐标系xOy中,如果抛物线y=ax2+bx+c上存在一点A,使点A关于坐标原点O的对称点A′也在这条抛物线上,那么我们把这条抛物线叫做回归抛物线,点A叫做这条抛物线的回归点.
(1)已知点M在抛物线y=﹣x2+2x+4上,且点M的横坐标为2,试判断抛物线y=﹣x2+2x+4是否为回归抛物线,并说明理由;
(2)已知点C为回归抛物线y=﹣x2﹣2x+c的顶点,如果点C是这条抛物线的回归点,求这条抛物线的表达式;
(3)在(2)的条件下,所求得的抛物线的对称轴与x轴交于点D.联结CO并延长,交该抛物线于点E,点F是射线CD上一点,如果∠CFE=∠DEC,求点F的坐标.
25.(14分)如图,在矩形ABCD中,AB=2,AD=1,点E在边AB上(点E与端点A、B不重合),联结DE,过点D作DF⊥DE,交BC的延长线于点F,联结EF,与对角线AC、边CD分别交于点G、H.设AE=x,DH=y.
(1)求证:△ADE∽△CDF,并求∠EFD的正切值;
(2)求y关于x的函数解析式,并写出该函数的定义域;
(3)联结BG,当△BGE与△DEH相似时,求x的值.
2020-2021学年上海市闵行区九年级(上)期末数学试卷(一模)
参考答案与试题解析
一、选择题(本大共6题,每题4分,满分24分)
1.下列函数中,是二次函数的是( )
A.y=﹣﹣3x B.y=﹣(x﹣1)2+x2
C.y=11x2+29x D.y=ax2+bx+c
【分析】利用二次函数定义进行分析即可.
【解答】解:A、含有分式,不是二次函数,故此选项不合题意;
B、y=﹣(x﹣1)2+x2=2x﹣1,不是二次函数,故此选项不合题意;
C、是二次函数,故此选项符合题意;
D、当a=0时,不是二次函数,故此选项不合题意;
故选:C.
【点评】此题主要考查了二次函数,关键是掌握判断函数是否是二次函数,首先是要看它的右边是否为整式,若是整式且仍能化简的要先将其化简,然后再根据二次函数的定义作出判断,要抓住二次项系数不为0这个关键条件.
2.已知在Rt△ABC中,∠C=90°,∠B=β,AB=5,那么AC的长为( )
A.5cosβ B.5sinβ C. D.
【分析】根据锐角三角函数的定义即可得出答案.
【解答】解:在Rt△ABC中,∵∠C=90°,∠B=β,AB=5,
∴sinB=sinβ=,
∴AC=AB?sinβ=5sinβ,
故选:B.
【点评】本题考查锐角三角函数的定义,理解锐角三角函数的意义是解决问题的关键.
3.如图,在平面直角坐标系xOy中,二次函数y=ax2+bx+c图象经过点O(0,0),那么根据图象,下列判断正确的是( )
A.a<0 B.b>0 C.ab>0 D.c=0
【分析】根据抛物线的开口方向,对称轴以及与y轴的交点进行判断即可.
【解答】解:∵抛物线开口向上,
∴a>0,故A错误;
∵﹣>0,a>0,
∴b<0,故B错误;
∵a>0,b<0,
∴ab<0,故C错误;
∵图象经过点O(0,0),
∴c=0,故D正确;
故选:D.
【点评】本题考查了二次函数的图象与系数的关系,对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向.当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c).抛物线与x轴交点个数由△决定:△=b2﹣4ac>0时,抛物线与x轴有2个交点;△=b2﹣4ac=0时,抛物线与x轴有1个交点;△=b2﹣4ac<0时,抛物线与x轴没有交点.
4.以下说法错误的是( )
A.如果k=,那么=
B.如果=﹣2,那么||=2||
C.如果=(为非零向量),那么∥
D.如果是与非向量同方向的单位向量,那么=||.
【分析】根据共线向量的定义,零向量的意义进行判断.
【解答】解:A、如果k=,那么k=0,故本选项符合题意.
B、如果=﹣2,那么||=2||,故本选项不符合题意.
C、如果=(为非零向量),那么与方向相同,则∥,故本选项不符合题意.
D、如果是与非向量同方向的单位向量,那么=||,故本选项不符合题意.
故选:A.
【点评】本题主要考查了平面向量,注意:平面向量既有大小,又有方向.
5.已知⊙A与⊙B的半径分别是6和8,圆心距AB=2,那么⊙A与⊙B的位置关系是( )
A.相交 B.内切 C.外切 D.内含
【分析】求出两圆半径的和与差,再与圆心距比较大小,确定两圆位置关系;设两圆的半径分别为R和r,且R≥r,圆心距为d:外离,则d>R+r;外切,则d=R+r;相交,则R﹣r<d<R+r;内切,则d=R﹣r;内含,则d<R﹣r.
【解答】解:因为8﹣6=2,圆心距AB=2,
所以d=R﹣r,
所以两圆内切.
故选:B.
【点评】考查了圆与圆的位置关系,本题利用了两圆内切,则d=R﹣r.
6.古希腊艺术家发现当人的头顶至肚脐的长度(上半身的长度)与肚脐至足底的长度(下半身的长度)的比值为“黄金分割数”时,人体的身材是最优美的.一位女士身高为154cm,她上半身的长度为62cm,为了使自己的身材显得更为优美,计划选择一双合适的高跟鞋,使自己的下半身长度增加.你认为选择鞋跟高为多少厘米的高跟鞋最佳?( )
A.4cm B.6cm C.8cm D.10cm
【分析】她下半身的长度为92cm,设鞋跟高为x厘米时,她身材显得更为优美,利用黄金分割的定义得到≈0.618,然后解方程即可.
【解答】解:∵一位女士身高为154cm,她上半身的长度为62cm,
∴她下半身的长度为92cm,
设鞋跟高为x厘米时,她身材显得更为优美,
根据题意得≈0.618,
解得x≈8.3(cm).
经检验x=8.3为原方程的解,
所以选择鞋跟高为8厘米的高跟鞋最佳.
故选:C.
【点评】本题考查了因式分解的应用:利用因式分解解决求值问题.利用因式分解解决证明问题.利用因式分解简化计算问题.也考查了黄金分割.
二、填空题(本大题共12题,每题4分,满分48分)
7.如果2a=3b(b≠0),那么= .
【分析】根据比例的性质直接解答即可.
【解答】解:∵2a=3b(b≠0),
∴=.
故答案为:.
【点评】此题考查了比例的性质,熟练掌握两内项之积等于两外项之积是解题的关键.
8.化简:(﹣3+)+= ﹣+ .
【分析】先利用乘法结合律去括号,然后计算加减法.
【解答】解:原式=﹣++=﹣+.
故答案是:﹣+.
【点评】本题主要考查了平面向量,实数的运算法则同样能应用于平面向量的计算之中.
9.抛物线y=﹣x2﹣3x在对称轴的右侧部分是 下降 的(填“上升”或“下降”).
【分析】根据抛物线解析式可求得其开口方向和对称轴,结合抛物线的增减性可得到答案.
【解答】解:∵y=﹣x2﹣3x,
∴抛物线开口向下,对称轴为直线x=﹣=﹣,
∴在y轴右侧,y随x增大而减小,
∴其图象在y轴右侧部分是下降,
故答案为:下降.
【点评】本题主要考查二次函数的增减性,掌握开口向下的二次函数在对称轴右侧y随x的增大而减小是解题的关键.
10.将抛物线y=x2+2x向下平移1个单位,那么所得抛物线与y轴的交点的坐标为 (0,﹣1) .
【分析】根据“左加右减、上加下减”的原则写出新抛物线解析式,然后将二次函数解析式转化为方程,通过解解方程求解.
【解答】解:由“左加右减、上加下减”的原则可知,把抛物线y=x2+2x=(x+1)2﹣1的图象向下平移1个单位,则平移后的抛物线的表达式为y=x2+2x=(x+1)2﹣2,
令x=0,则y=﹣1.
所以所得抛物线与y轴的交点的坐标为(0,﹣1).
故答案是:(0,﹣1).
【点评】本题考查的是二次函数的图象与几何变换,要求熟练掌握平移的规律:左加右减,上加下减.
11.已知两个相似三角形的相似比为4:9,那么这两个三角形的周长之比为 4:9 .
【分析】直接利用相似三角形的周长比等于相似比,进而得出答案.
【解答】解:∵两个相似三角形的相似比为4:9,
∴它们的周长比等于相似比,即:4:9.
故答案为4:9.
【点评】本题考查对相似三角形性质的理解.(1)相似三角形周长的比等于相似比.(2)相似三角形面积的比等于相似比的平方.(3)相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.
12.在△ABC中,点D、E分别在边AB、AC上,且DE∥BC,如果,那么= .
【分析】由DE∥BC证△ADE∽△ABC,得==,继而可得答案.
【解答】解:如图,
∵DE∥BC,
∴△ADE∽△ABC,
∴==,
∴=,
故答案为:.
【点评】本题主要考查相似三角形的判定与性质,解题的关键是掌握相似三角形的判定和性质.
13.在直角坐标平面内有一点A(12,5),点A与原点O的连线与x轴的正半轴的夹角为θ,那么cosθ= .
【分析】根据题意,作出合适的平面直角坐标系,然后作AB⊥x轴于点B,再根据点的A的坐标和勾股定理,可以得到OA的长,然后即可得到cosθ的值.
【解答】解:作AB⊥x轴于点B,如右图所示,
∵点A(12,5),
∴OB=12,AB=5,∠ABO=90°,
∴OA==13,
∴cos∠AOB=,
即cosθ=,
故答案为:.
【点评】本题考查解直角三角形、勾股定理、锐角三角函数,解答本题的关键是明确题意,利用数形结合的思想解答.
14.如果港口A的南偏东52°方向有一座小岛B,那么从小岛B观察港口A的方向是 北偏西52° .
【分析】根据方位角的概念,画图正确表示出方位角,即可求解.
【解答】解:如图,∵∠1=∠2=52°,
∴从小岛B观察港口A的方向是北偏西52°.
故答案为:北偏西52°.
【点评】此题主要考查了方向角,正确画出方位角,根据平行线的性质解答是解题关键.
15.正六边形的边心距与半径的比值为 .
【分析】设正六边形的半径与外接圆的半径相等,构建直角三角形利用勾股定理即可求出边心距.
【解答】解:设正六边形的半径是r,则外接圆的半径r,内切圆的半径是正六边形的边心距,因而是,则可知正六边形的边心距与半径的比值为.
【点评】正多边形的计算一般是通过中心作边的垂线,连接半径,把正多边形中的半径,边长,边心距,中心角之间的计算转化为解直角三角形.
16.如图,在△ABC中,AB=2AC,点D在边AB上,且∠ACD=∠B,那么= .
【分析】根据相似三角形面积的比等于相似比的平方即可得结论.
【解答】解:∵∠ACD=∠B,∠A=∠A,
∴△ACD∽△ABC,
∴=()2=()2=.
故答案为:.
【点评】本题考查了相似三角形的判定与性质,解决本题的关键是掌握相似三角形的判定与性质.
17.如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,点P在边AC上,⊙P的半径为1.如果⊙P与边BC和边AB都没有公共点,那么线段PC长的取值范围是 1<CP< .
【分析】根据勾股定理得到AC=4,当⊙P与AB相切时,设切点为D,如图,连接PD,则PD⊥AB,根据相似三角形的性质可得到结论.
【解答】解:在Rt△ABC中,∠ACB=90°,AB=5,BC=3,
∴AC=4,
当⊙P与AB相切时,设切点为D,如图,
连接PD,
则PD⊥AB,
∴∠C=∠ADP=90°,
∵∠A=∠A,
∴△ADP∽△ACB,
∴,
∴=,
∴PA=,
∴PC=AC﹣PA=,
∴线段PC长的取值范围是1<CP<,
故答案为:1<CP<.
【点评】本题考查了直线与圆的位置关系,相似三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.
18.如图,在Rt△ABC中,∠ACB=90°,AB=3,tanB=.将△ABC绕着点A顺时针旋转后,点B恰好落在射线CA上的点D处,点C落在点E处,射线DE与边AB相交于点F,那么BF= 3﹣ .
【分析】过点F作FG⊥AC于点G,由旋转的性质得出∠B=∠D,得出tan∠B=tan∠D=,由平行线的性质得出∠B=∠AFG,设AG=x,则FG=2x,则,求出AG=1,则可得出答案.
【解答】解:如图,过点F作FG⊥AC于点G,
∵将△ABC绕着点A顺时针旋转后,点B恰好落在射线CA上的点D处,
∴∠B=∠D,
∴tan∠B=tan∠D=,
∵∠ACB=∠FGA=90°,
∴BC∥FG,
∴∠B=∠AFG,
∴tan∠B=tan∠AFG=,
设AG=x,则FG=2x,
∴,
解得x=1,
∴AG=1,FG=2,
∴AF===,
∴BF=AB﹣AF=3﹣.
故答案为:3﹣.
【点评】本题考查了旋转的性质,直角三角形的性质,锐角三角函数的定义,勾股定理,熟练掌握旋转的性质是解题的关键.
三、解答题(本大题共7题,满分78分)
19.(10分)计算:2cos60°﹣cot30°+.
【分析】直接利用特殊角的三角函数值以及二次根式的性质化简得出答案.
【解答】解:原式=2×﹣+
=1﹣+
=1﹣+
=1﹣++1
=2.
【点评】此题主要考查了特殊角的三角函数值二次根式的混合运算,正确化简各数是解题关键.
20.(10分)如图,在平行四边形ABCD中,对角线AC、BD相交于点O.E为OC的中点,联结BE并延长,交边CD于点F.设=,=.
(1)填空:向量= ﹣ ;
(2)填空:向量= + ,并在图中画出向量在向量和方向上的分向量.
(注:本体结果用含向量、的式子表示,画图不要求写作法,但要指出所作图中表示结论的向量)
【分析】(1)利用三角形法则求出,再证明AE=AC即可解决问题.
(2)利用平行线分线段成比例定理,求出,再利用三角形法则即可解决问题.
【解答】解:(1)∵=+,=,=.
∴=﹣,
∵四边形ABCD是平行四边形,
∴OA=OC,
∵OE=EC,
∴AE=AC,
∴=﹣.
故答案为:﹣.
(2)∵CF∥AB,
∴CF:AB=EC:AE=1:3,
∴CF=BA,
∴=,
∴=+=+.
在向量和方向上的分向量分别为和.
故答案为:+.
【点评】本题考查作图﹣复杂作图,平四边形的性质,平面向量,三角形法则,平行四边形法则等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
21.(10分)如图,⊙O是△BC的外接圆,AB长为4,AB=AC,联结CO并延长,交边AB于点D,交AB于点E,且E为弧AB的中点.求:
(1)边BC的长;
(2)⊙O的半径.
【分析】(1)利用垂径定理的推论可判断CD垂直平分AB,所以CB=CA=4;
(2)连接OB,如图,先证明ABC为等边三角形得到∠A=60°,利用圆周角定理得到∠BOC=120°,则∠BOD=60°,然后利用含30度的直角三角形三边的关系求出OB即可.
【解答】解:(1)∵E点为的中点,CE为直径,
∴CE⊥AB,
∴AD=BD,
即CD垂直平分AB,
∴CB=CA=4;
(2)连接OB,如图,
∵AB=BC=AC,
∴△ABC为等边三角形,
∴∠A=60°,
∴∠BOC=2∠A=120°,
∴∠BOD=60°,
在Rt△BOD中,BD=AB=2,
∴OD=BD=,
∴OB=2OD=,
即⊙O的半径为.
【点评】本题考查了三角形的外接圆与外心:三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.也考查了圆周角定理.
22.(10分)为了监控大桥下坡路段车辆行驶速度,通常会在下引桥处设置电子眼进行区间测速.如图,电子眼位于点P处,离地面的铅锤高度PQ为9米,区间测速的起点为下引桥坡面点A处,此时电子眼的俯角为30°;区间测速的终点为下引桥坡脚点B处,此时电子眼的俯角为60°(A、B、P、Q四点在同一平面).
(1)求路段BQ的长(结果保留根号);
(2)当下引桥坡度i=1:2时,求电子眼区间测速路段AB的长(结果保留根号).
【分析】(1)根据 BQ=PQ?tan∠BPQ,求解即可.
(2)如图,过点A作AM⊥QB于M,AH⊥PQ于H.由题意,∠PAH=∠TPA=30°,设AM=a米,则BM=2a米,在Rt△APH中,根据tan∠PAH=,构建方程求出a,再利用勾股定理求出AB即可.
【解答】解:(1)由题意,∠PBQ=∠TPB=60°,
∵∠PQB=90°,
∴∠BPQ=30°,
∴BQ=PQ?tan30°=9×=3(米).
(2)如图,过点A作AM⊥QB于M,AH⊥PQ于H.
由题意,∠PAH=∠TPA=30°,
设AM=a米,则BM=2a米,
∵∠AHQ=∠HQM=∠AMQ=90°,
∴四边形AHQM是矩形,
∴AH=QM=(3+2a)米,QH=AM=a米,PH=PQ﹣HQ=(9﹣a)米,
在Rt△APH中,tan∠PAH=,
∴=,
解得a=2,
∴AM=2(米),BM=4(米),
∴AB===2(米).
【点评】本题考查解直角三角形的应用﹣仰角俯角问题,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
23.(12分)如图,点E为△ABC边BC上一点,过点C作CD⊥BA,交BA的延长线于点D,交EA的延长线于点F,且AF?CD=BC?AD.
(1)求证:AE⊥BC;
(2)如果BE=CE,求证:BC2=2BD?AC.
【分析】(1)通过证明△ADF∽△CDB,可得∠F=∠B,由余角的性质可求解;
(2)通过证明△ABE∽△CBD,可得,可得结论.
【解答】证明:(1)∵AF?CD=BC?AD,
∴,
又∵∠ADF=∠BDC,
∴△ADF∽△CDB,
∴∠F=∠B,
∵∠B+∠BCD=90°,
∴∠F+∠BCD=90°,
∴AE⊥BC;
(2)∵BE=CE,AE⊥BC,
∴AB=AC,
∵∠ABE=∠DBC,∠BDC=∠AEB=90°,
∴△ABE∽△CBD,
∴,
∴BC?BC=AB?BD,
∴BC2=2BD?AC.
【点评】本题考查了相似三角形的判定和性质,掌握相似三角形的判定定理是本题的关键.
24.(12分)在平面直角坐标系xOy中,如果抛物线y=ax2+bx+c上存在一点A,使点A关于坐标原点O的对称点A′也在这条抛物线上,那么我们把这条抛物线叫做回归抛物线,点A叫做这条抛物线的回归点.
(1)已知点M在抛物线y=﹣x2+2x+4上,且点M的横坐标为2,试判断抛物线y=﹣x2+2x+4是否为回归抛物线,并说明理由;
(2)已知点C为回归抛物线y=﹣x2﹣2x+c的顶点,如果点C是这条抛物线的回归点,求这条抛物线的表达式;
(3)在(2)的条件下,所求得的抛物线的对称轴与x轴交于点D.联结CO并延长,交该抛物线于点E,点F是射线CD上一点,如果∠CFE=∠DEC,求点F的坐标.
【分析】(1)先求出点M坐标,M'的坐标,代入解析式可求解;
(2)先求出点C坐标,C'的坐标,利用回归点的定义可求解;
(3)通过证明△CEF∽△CDE,可得,可求CF=10,即可求解.
【解答】解:(1)抛物线y=﹣x2+2x+4是回归抛物线,
理由如下:∵点M在抛物线y=﹣x2+2x+4上,
∴y=﹣4+4+4=4,
∴点M(2,4),
∴点M关于坐标原点O的对称点M'(﹣2,﹣4),
当x=﹣2时,y=﹣4﹣4+4=﹣4,
∴点M'在抛物线上,
∴抛物线y=﹣x2+2x+4是回归抛物线;
(2)∵点C为回归抛物线y=﹣x2﹣2x+c的顶点,
∴点C(﹣1,c+1),
∴点C关于原点O的对称点C'(1,﹣c﹣1),
∵点C是这条抛物线的回归点,
∴﹣c﹣1=﹣1﹣2+c,
∴c=1,
∴抛物线解析式为:y=﹣x2﹣2x+1;
(3)∵抛物线y=﹣x2﹣2x+1,
∴对称点为x=﹣1,
∴点D(﹣1,0),点C(﹣1,2),
∴直线CO解析式为y=﹣2x,
联立方程组,
∴,,
点E(1,﹣2),
在△CEF和△CDE中,∠CFE=∠CED,∠FCE=∠ECD,
∴△CEF∽△CDE,
∴,
∴CE2=CD?CF,
∴(﹣1﹣1)2+(2+2)2=2CF,
∴CF=10,
∴F(﹣1,﹣8).
【点评】本题是二次函数综合题,考查了二次函数的性质,相似三角形的判定和性质,理解新定义并运用是解题的关键.
25.(14分)如图,在矩形ABCD中,AB=2,AD=1,点E在边AB上(点E与端点A、B不重合),联结DE,过点D作DF⊥DE,交BC的延长线于点F,联结EF,与对角线AC、边CD分别交于点G、H.设AE=x,DH=y.
(1)求证:△ADE∽△CDF,并求∠EFD的正切值;
(2)求y关于x的函数解析式,并写出该函数的定义域;
(3)联结BG,当△BGE与△DEH相似时,求x的值.
【分析】(1)根据矩形的性质得到∠ADC=∠DCB=90°,根据余角的性质得到∠ADE=∠CDF,由相似三角形的判定定理即可得到结论;
(2)根据矩形的性质和相似三角形的判定和性质解答;
(3)根据相似三角形的性质分两种情况解答.
【解答】解:(1)∵∠ADE+∠CDE=90°,∠CDF+∠CDE=90°,
∴∠ADE=∠CDF,
在Rt△EAD与Rt△FCD中,
,
∴△FAD∽△FCD,
∴,
∴tan∠EFD=,
(2)由(1)可知FC=2EA=2x,
∵四边形ABCD是矩形,
∴AB∥CD,
∴△FCH∽△FBE,
∴,
∴,
可得:y=(0<x<2);
(3)BE=2﹣x,DH=y,DE=,EH=,
∴,
∴EG=,
∵∠BEG=∠DHE,
若△BEG∽△DHE,则有两种情况,
第一种:
∵∠EGB=∠HED,
∴,
∴,
即,
解得:x=,
第二种:
∵∠EGB=∠HDE,
∴,
∴,
即,
解得:x=1.5.
综上所述,x的值为或1.5.
【点评】本题考查了相似综合题,综合运用了相似三角形的判定和性质,求函数的解析式,矩形的性质等知识点,熟练掌握相似三角形的判定和性质是解题的关键.
同课章节目录
