2020-2021学年人教版八年级数学下册17.1勾股定理提高卷B(word版含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册17.1勾股定理提高卷B(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 422.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 14:46:49 | ||
图片预览




文档简介
17.1勾股定理提高卷B
一、单选题
1.如图所示,一场暴雨过后,垂直于地面的一棵大树在距地面5米的C处折断,树尖B恰好碰到地面,经测量树尖B与树桩A相距12米,则大树折断前高为( )
A.13米
B.17米
C.18米
D.22米
2.下列各组数是勾股数的是( )
A.0.3,0.4,0.5
B.5,7,9
C.4,5,6
D.6,8,10
3.如图
,点
A
表示的实数是(
)
A.
B.
C.
D.
4.我国古代著名的“赵爽弦图”的示意图如图所示,它是由四个全等的直角三角形围成的.若AC=2,BC=3,将四个直角三角形中边长为3的直角边分别向外延长一倍,得到一个如图所示“数学风车”,则这个风车的外围周长是(
)
A.
B.8
C.
D.
5.如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=15cm,其斜边上的高为( )
A.17cm
B.8.5cm
C.cm
D.cm
6.如图,在灯塔O的东北方向8海里处有一轮船A,在灯塔的东南方向6海里处有一渔船B,则AB间的距离为( )
A.9海里
B.10海里
C.11海里
D.12海里
7.小明学了在数轴上表示无理数的方法后,进行了练习:首先画数轴,原点为O,在数轴上找到表示数2的点A,然后过点A作AB⊥OA,使AB=1;再以O为圆心,OB的长为半径作弧,交数轴正半轴于点P,那么点P表示的数是( )
A.2.2
B.
C.
D.
8.如图四边形,,,,则的值为(
)
A.6
B.
C.
D.7
9.有一块直角三角形纸片,两直角边AC=12cm,BC=16cm如图,现将直角边AC沿AD折叠,使它落在斜边AB上,且与AE重合,则DE等于( )
A.6cm
B.8cm
C.10cm
D.14cm
10.如图,四边形
ABCD
中,AD∥BC,∠B=90°,E
为
AB
上一点,分别以
ED,EC
为折痕将两个角(∠A,∠B)向内折起,点
A,B
恰好落在
CD
边的点
F
处.若
AD=4,BC=7,则
EF
的值是(
)
A.2
B.4
C.2
D.4
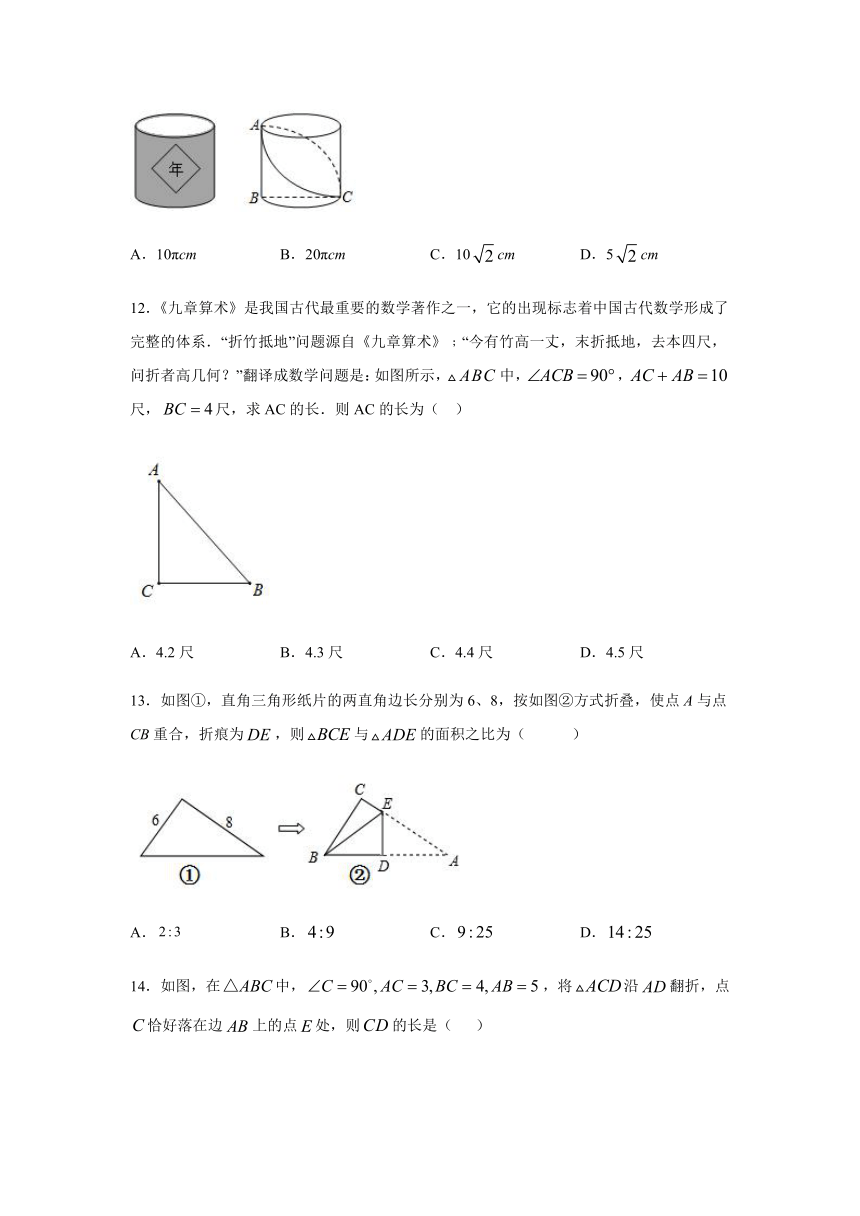
11.如图,小彬到雁江区高洞产业示范村参观,看到一个贴有大红“年”字的圆柱状粮仓非常漂亮,回家后小彬制作了一个底面周长为10cm,高为5cm的圆柱粮仓模型.如图BC是底面直径,AB是高.现要在此模型的侧面贴一圈彩色装饰带,使装饰带经过A,C两点(接头不计),则装饰带的长度最短为( )
A.10πcm
B.20πcm
C.10cm
D.5cm
12.《九章算术》是我国古代最重要的数学著作之一,它的出现标志着中国古代数学形成了完整的体系.“折竹抵地”问题源自《九章算术》﹔“今有竹高一丈,末折抵地,去本四尺,问折者高几何?”翻译成数学问题是:如图所示,中,,尺,尺,求AC的长.则AC的长为(
)
A.4.2尺
B.4.3尺
C.4.4尺
D.4.5尺
13.如图①,直角三角形纸片的两直角边长分别为6、8,按如图②方式折叠,使点A与点CB重合,折痕为,则与的面积之比为( )
A.
B.
C.
D.
14.如图,在中,,将沿翻折,点恰好落在边上的点处,则的长是(
)
A.1
B.
C.
D.2
15.如图所示,是一张直角三角形的纸片,两直角边AC=6㎝,BC=8㎝,现将△ABC折叠,使点B与点A重合,折痕为DE,则AD的长为(
)
A.4㎝
B.5㎝
C.6㎝
D.㎝
16.如图,在中,,点是边的中点,连结,将沿直线翻折得到,连结.若,,则线段的长为(
)
A.
B.
C.
D.
17.在中,,,边上的高,则另一边等于(
)
A.
B.
C.或
D.或
18.如图,已知四边形ABCD中,AC平分∠BAD,AB=AC=5,AD=3,BC=CD.则点C到AB的距离是(
)
A.
B.
C.3
D.2
19.1.一块直角三角形木板,它的一条直角边AC长为1cm,面积为1cm2
,
甲、乙两人分别按图①、②把它加工成一个正方形桌面,则①、②中正方形的面积较大的是(??
)
A.?①????????????????????????????????????B.?②????????????????????????????????????C.?一样大????????????????????D.?无法判断
20.如图,在中,,点在边上,把沿翻折,点恰好与上的点重合,若,则的周长为(
)
A.8
B.
C.
D.
二、填空题
21.使用13米长的梯子登建筑物,如果梯子的底部离建筑物的底部的距离不能小于5米,问该梯子最多可登上_____
米高的建筑物.
22.在直角三角形ABC中,斜边,则________.
23.底角为45°的等腰三角形一边长为4cm,则此等腰三角形的底边长=_________cm.
24.如图,△ABC中AD⊥BC于D,AC=2,
DC=1,BD=3,
则AB的长为_____.
25.如图,,点D、E为边上的两点,且,连接、,已知,则的长为_________.
三、解答题
26.如图,一个梯子长25米,顶端靠在墙上(墙与地面垂直),这时梯子下端与墙角距离为7米.
(1)求梯子顶端与地面的距离的长;
(2)若梯子的顶端下滑到,使,求梯子的下端滑动的距离的长.
27.综合与探究
在学习了轴对称变换后,我们经常会遇到三角形中的“折叠”问题,在解答这种问题时,通常会考虑到折叠前与折叠后的图形全等,并利用全等图形的性质,即对应角相等,对应边相等来研究解决数学中的“折叠”问题,每个小组剪了一些如图1所示的纸片(,,)并进行探究:
(1)如图2,“奋斗”小组将纸片沿DE折叠,使点C落在外部的处
①若,,则的度数为
.
②,,之间的数量关系为
.
(2)如图3,“勤奋”小组将沿DE折叠,使点C与点A重合,求BD的长;
(3)如图4,“雄鹰”小组将沿AD折叠,使点B落在点E处,连接CE,当为直角三角形时,求BD的长.
28.如图,在四边形ABCD中,AB=BC=1,CD=,DA=1,且∠B=90°.求:
(1)∠BAD的度数;
(2)四边形ABCD的面积(结果保留根号);
(3)将△ABC沿AC翻折至△AB′C,如图所示,连接B′D,求四边形ACB′D的面积.
29.已知中,,以和为边向外作等边和等边.
(1)连接、,如图,求证:;
(2)若为中点,连接,如图,求证:;
(3)若,延长交于,,如图,则
.(直接写出结果)
参考答案
1--10CDCDD
BBBAA
11--20CADCD
ACCAC
21.12
22.
23.4或
24.
25.
26.(1)24米;(2)梯子的下端滑动的距离的长为8米.
27.(1)①114°;②∠2=∠1+2∠C;(2);(3)3或6
28.(1)135°;(2)(+1);(3)(2+)
29.(1)证明:∵等边和等边.
AB=DB,BC=BE,∠ABD=∠CBE=60°,
∴∠ABD+∠ABC=∠CBE+∠ABC,
∴∠ABE=∠DBC,
,
;
(2)延长使,连接,
∵为中点,
∴CN=DN,
又∠AND=∠FNC,
,
,,
∵,∠DAB=60°,
∴∠DAC=120°,
∴,
,
∵AC=CA,
,
;
(3)过E作EG⊥BE,交AM延长线于G,
∴,,,
∴AC=2,
由勾股定理得:BC=,
∴∠EBM=180°-∠ABC-∠CBE=30°,
∴∠G=180°-∠GBE-∠BEG=60°=∠CAB,
∵BC=EB,
∴△CAB≌△BGE(AAS),
∴GE=AB=,
∴BG=2GE=2,
∵∠DAM=60°=∠G,
又∵∠AMD=∠GME,
∴△AD≌△GME(AAS),
∴AM=GM,
∴GM=AB+BM,
∴BG=BM+GM=2BM+AB=2,
∴2BM+=2,
∴.
故答案为:.
一、单选题
1.如图所示,一场暴雨过后,垂直于地面的一棵大树在距地面5米的C处折断,树尖B恰好碰到地面,经测量树尖B与树桩A相距12米,则大树折断前高为( )
A.13米
B.17米
C.18米
D.22米
2.下列各组数是勾股数的是( )
A.0.3,0.4,0.5
B.5,7,9
C.4,5,6
D.6,8,10
3.如图
,点
A
表示的实数是(
)
A.
B.
C.
D.
4.我国古代著名的“赵爽弦图”的示意图如图所示,它是由四个全等的直角三角形围成的.若AC=2,BC=3,将四个直角三角形中边长为3的直角边分别向外延长一倍,得到一个如图所示“数学风车”,则这个风车的外围周长是(
)
A.
B.8
C.
D.
5.如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=15cm,其斜边上的高为( )
A.17cm
B.8.5cm
C.cm
D.cm
6.如图,在灯塔O的东北方向8海里处有一轮船A,在灯塔的东南方向6海里处有一渔船B,则AB间的距离为( )
A.9海里
B.10海里
C.11海里
D.12海里
7.小明学了在数轴上表示无理数的方法后,进行了练习:首先画数轴,原点为O,在数轴上找到表示数2的点A,然后过点A作AB⊥OA,使AB=1;再以O为圆心,OB的长为半径作弧,交数轴正半轴于点P,那么点P表示的数是( )
A.2.2
B.
C.
D.
8.如图四边形,,,,则的值为(
)
A.6
B.
C.
D.7
9.有一块直角三角形纸片,两直角边AC=12cm,BC=16cm如图,现将直角边AC沿AD折叠,使它落在斜边AB上,且与AE重合,则DE等于( )
A.6cm
B.8cm
C.10cm
D.14cm
10.如图,四边形
ABCD
中,AD∥BC,∠B=90°,E
为
AB
上一点,分别以
ED,EC
为折痕将两个角(∠A,∠B)向内折起,点
A,B
恰好落在
CD
边的点
F
处.若
AD=4,BC=7,则
EF
的值是(
)
A.2
B.4
C.2
D.4
11.如图,小彬到雁江区高洞产业示范村参观,看到一个贴有大红“年”字的圆柱状粮仓非常漂亮,回家后小彬制作了一个底面周长为10cm,高为5cm的圆柱粮仓模型.如图BC是底面直径,AB是高.现要在此模型的侧面贴一圈彩色装饰带,使装饰带经过A,C两点(接头不计),则装饰带的长度最短为( )
A.10πcm
B.20πcm
C.10cm
D.5cm
12.《九章算术》是我国古代最重要的数学著作之一,它的出现标志着中国古代数学形成了完整的体系.“折竹抵地”问题源自《九章算术》﹔“今有竹高一丈,末折抵地,去本四尺,问折者高几何?”翻译成数学问题是:如图所示,中,,尺,尺,求AC的长.则AC的长为(
)
A.4.2尺
B.4.3尺
C.4.4尺
D.4.5尺
13.如图①,直角三角形纸片的两直角边长分别为6、8,按如图②方式折叠,使点A与点CB重合,折痕为,则与的面积之比为( )
A.
B.
C.
D.
14.如图,在中,,将沿翻折,点恰好落在边上的点处,则的长是(
)
A.1
B.
C.
D.2
15.如图所示,是一张直角三角形的纸片,两直角边AC=6㎝,BC=8㎝,现将△ABC折叠,使点B与点A重合,折痕为DE,则AD的长为(
)
A.4㎝
B.5㎝
C.6㎝
D.㎝
16.如图,在中,,点是边的中点,连结,将沿直线翻折得到,连结.若,,则线段的长为(
)
A.
B.
C.
D.
17.在中,,,边上的高,则另一边等于(
)
A.
B.
C.或
D.或
18.如图,已知四边形ABCD中,AC平分∠BAD,AB=AC=5,AD=3,BC=CD.则点C到AB的距离是(
)
A.
B.
C.3
D.2
19.1.一块直角三角形木板,它的一条直角边AC长为1cm,面积为1cm2
,
甲、乙两人分别按图①、②把它加工成一个正方形桌面,则①、②中正方形的面积较大的是(??
)
A.?①????????????????????????????????????B.?②????????????????????????????????????C.?一样大????????????????????D.?无法判断
20.如图,在中,,点在边上,把沿翻折,点恰好与上的点重合,若,则的周长为(
)
A.8
B.
C.
D.
二、填空题
21.使用13米长的梯子登建筑物,如果梯子的底部离建筑物的底部的距离不能小于5米,问该梯子最多可登上_____
米高的建筑物.
22.在直角三角形ABC中,斜边,则________.
23.底角为45°的等腰三角形一边长为4cm,则此等腰三角形的底边长=_________cm.
24.如图,△ABC中AD⊥BC于D,AC=2,
DC=1,BD=3,
则AB的长为_____.
25.如图,,点D、E为边上的两点,且,连接、,已知,则的长为_________.
三、解答题
26.如图,一个梯子长25米,顶端靠在墙上(墙与地面垂直),这时梯子下端与墙角距离为7米.
(1)求梯子顶端与地面的距离的长;
(2)若梯子的顶端下滑到,使,求梯子的下端滑动的距离的长.
27.综合与探究
在学习了轴对称变换后,我们经常会遇到三角形中的“折叠”问题,在解答这种问题时,通常会考虑到折叠前与折叠后的图形全等,并利用全等图形的性质,即对应角相等,对应边相等来研究解决数学中的“折叠”问题,每个小组剪了一些如图1所示的纸片(,,)并进行探究:
(1)如图2,“奋斗”小组将纸片沿DE折叠,使点C落在外部的处
①若,,则的度数为
.
②,,之间的数量关系为
.
(2)如图3,“勤奋”小组将沿DE折叠,使点C与点A重合,求BD的长;
(3)如图4,“雄鹰”小组将沿AD折叠,使点B落在点E处,连接CE,当为直角三角形时,求BD的长.
28.如图,在四边形ABCD中,AB=BC=1,CD=,DA=1,且∠B=90°.求:
(1)∠BAD的度数;
(2)四边形ABCD的面积(结果保留根号);
(3)将△ABC沿AC翻折至△AB′C,如图所示,连接B′D,求四边形ACB′D的面积.
29.已知中,,以和为边向外作等边和等边.
(1)连接、,如图,求证:;
(2)若为中点,连接,如图,求证:;
(3)若,延长交于,,如图,则
.(直接写出结果)
参考答案
1--10CDCDD
BBBAA
11--20CADCD
ACCAC
21.12
22.
23.4或
24.
25.
26.(1)24米;(2)梯子的下端滑动的距离的长为8米.
27.(1)①114°;②∠2=∠1+2∠C;(2);(3)3或6
28.(1)135°;(2)(+1);(3)(2+)
29.(1)证明:∵等边和等边.
AB=DB,BC=BE,∠ABD=∠CBE=60°,
∴∠ABD+∠ABC=∠CBE+∠ABC,
∴∠ABE=∠DBC,
,
;
(2)延长使,连接,
∵为中点,
∴CN=DN,
又∠AND=∠FNC,
,
,,
∵,∠DAB=60°,
∴∠DAC=120°,
∴,
,
∵AC=CA,
,
;
(3)过E作EG⊥BE,交AM延长线于G,
∴,,,
∴AC=2,
由勾股定理得:BC=,
∴∠EBM=180°-∠ABC-∠CBE=30°,
∴∠G=180°-∠GBE-∠BEG=60°=∠CAB,
∵BC=EB,
∴△CAB≌△BGE(AAS),
∴GE=AB=,
∴BG=2GE=2,
∵∠DAM=60°=∠G,
又∵∠AMD=∠GME,
∴△AD≌△GME(AAS),
∴AM=GM,
∴GM=AB+BM,
∴BG=BM+GM=2BM+AB=2,
∴2BM+=2,
∴.
故答案为:.
