第三章 圆 第一讲 圆的基本性质及位置关系
文档属性
| 名称 | 第三章 圆 第一讲 圆的基本性质及位置关系 |
|
|
| 格式 | zip | ||
| 文件大小 | 57.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-21 00:00:00 | ||
图片预览

文档简介
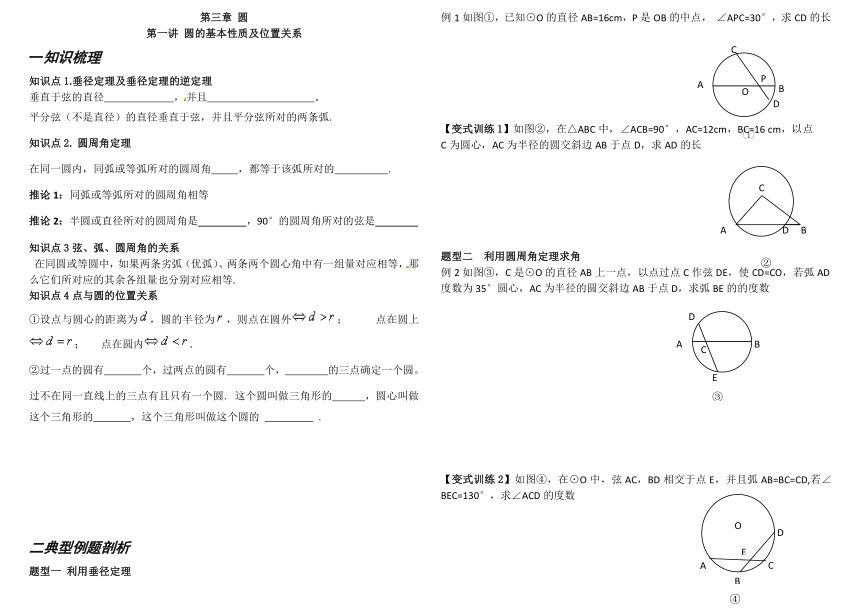
第三章 圆
第一讲 圆的基本性质及位置关系
一知识梳理
知识点1.垂径定理及垂径定理的逆定理
垂直于弦的直径 ,并且 .
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
知识点2. 圆周角定理
在同一圆内,同弧或等弧所对的圆周角 ,都等于该弧所对的 .
推论1:同弧或等弧所对的圆周角相等
推论2:半圆或直径所对的圆周角是 ,90°的圆周角所对的弦是
知识点3弦、弧、圆周角的关系
在同圆或等圆中,如果两条劣弧(优弧)、两条两个圆心角中有一组量对应相等,那么它们所对应的其余各组量也分别对应相等.
知识点4点与圆的位置关系
①设点与圆心的距离为,圆的半径为,则点在圆外; 点在圆上; 点在圆内.
②过一点的圆有 个,过两点的圆有 个, 的三点确定一个圆。
过不在同一直线上的三点有且只有一个圆. 这个圆叫做三角形的 ,圆心叫做这个三角形的 ,这个三角形叫做这个圆的 .
二典型例题剖析
题型一 利用垂径定理
例1如图①,已知⊙O的直径AB=16cm,P是OB的中点, ∠APC=30°,求CD的长
【变式训练1】如图②,在△ABC中,∠ACB=90°,AC=12cm,BC=16 cm,以点
C为圆心,AC为半径的圆交斜边AB于点D,求AD的长
题型二 利用圆周角定理求角
例2如图③,C是⊙O的直径AB上一点,以点过点C作弦DE,使CD=CO,若弧AD度数为35°圆心,AC为半径的圆交斜边AB于点D,求弧BE的的度数
【变式训练2】如图④,在⊙O中,弦AC,BD相交于点E,并且弧AB=BC=CD,若∠BEC=130°,求∠ACD的度数
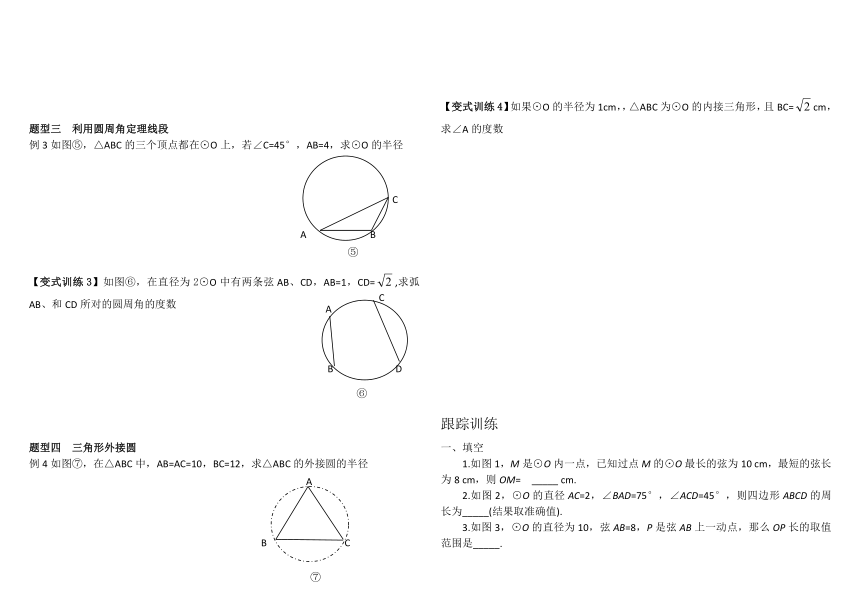
题型三 利用圆周角定理线段
例3如图⑤,△ABC的三个顶点都在⊙O上,若∠C=45°,AB=4,求⊙O的半径
【变式训练3】如图⑥,在直径为2⊙O中有两条弦AB、CD,AB=1,CD=,求弧AB、和CD所对的圆周角的度数
题型四 三角形外接圆
例4如图⑦,在△ABC中,AB=AC=10,BC=12,求△ABC的外接圆的半径
【变式训练4】如果⊙O的半径为1cm,,△ABC为⊙O的内接三角形,且BC=cm,求∠A的度数
跟踪训练
一、填空
1.如图1,M是⊙O内一点,已知过点M的⊙O最长的弦为10 cm,最短的弦长为8 cm,则OM=?_____ cm.?
2.如图2,⊙O的直径AC=2,∠BAD=75°,∠ACD=45°,则四边形ABCD的周长为_____(结果取准确值).
3.如图3,⊙O的直径为10,弦AB=8,P是弦AB上一动点,那么OP长的取值范围是_____.
图1 图2 图3
4.如图4,在⊙O中,两弦AD∥BC,AC、BD相交于点E,连接AB、CD,图中的全等三角形共有_____对.相似比不等于1的相似三角形共有_____对.
5.如图5,在⊙O中,直径AB和弦CD的长分别为10 cm和8 cm,则A、B两点到直线CD的距离之和是_____.
图4 图5
二、选择
6.如图6,点P是半径为5的⊙O内一点,且OP=4,在过P点的所有⊙O的弦中,你认为弦长为整数的弦的条数为
A.6条 B.5条 C.4条 D.2条
7.如图7,在平面直角坐标系中,⊙O′与两坐标分别交于A、B、C、D四点,已知:A(6,0),B(0,-3),C(-2,0),则点D的坐标为
A.(0,2) B.(0,3) C.(0,4) D.(0,5)
图6 图7 图8
8.如图8,已知AB和CD分别是半圆O的直径和弦,AD和BC相交于点E,若∠AEC=α,则
S△CDE∶S△ABE等于
A.sin2α B.cos2α C.tan2α D.与α无关
9.如图9,每张方格纸上都画有一个圆,只用不带刻度的直尺就能确定圆心位置的是
图9
10.如图10,已知:AB=,BC=2,CD=1,∠ABC=45°,则四边形ABCD的面积为
A. B. C. D.
图10
11.如图,现需测量一井盖(圆形)的直径,但只有一把角尺(尺的两边互相垂直,一边有刻度,且两边长度都长于井盖的半径),请配合图形,用文字说明测量方案,写出测量的步骤.(要求写出两种测量方案)
12如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.
(1)P是上一点(不与C、D重合),求证:∠CPD=∠COB.
(2)点P′在劣弧CD上(不与C、D重合)时,∠CP′D与∠COB有什么数量关系?请证明你的结论.
参考答案
一、1. 3 2. 1+2 3. 3≤OP≤5 4. 3 1 5.6 cm
二、6.B 7.C 8.B 9.A 10.D
三、11.方案1:使角尺顶点在圆上,角尺两边与圆两交点连接就是圆的直径,用刻度尺量出直径.
方案2:任画圆的一条弦,用尺量出弦的中点,利用角尺过弦中点做弦的垂线,垂线与圆的两交点间的线段为圆的直径.
12.(1)证明:连结OD, ∵AB是直径,AB⊥CD, ∴=.
∴∠COB=∠DOB=∠COD.
又∵∠CPD=∠COD, ∴∠CPD=∠COB.
(2)略
A
P
O
D
C
B
A
D
C
B
②
A
E
D
C
B
③
A
B
E
C
D
O
④
C
A
B
⑤
A
C
B
D
⑥
A
C
B
⑦⑦
第一讲 圆的基本性质及位置关系
一知识梳理
知识点1.垂径定理及垂径定理的逆定理
垂直于弦的直径 ,并且 .
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
知识点2. 圆周角定理
在同一圆内,同弧或等弧所对的圆周角 ,都等于该弧所对的 .
推论1:同弧或等弧所对的圆周角相等
推论2:半圆或直径所对的圆周角是 ,90°的圆周角所对的弦是
知识点3弦、弧、圆周角的关系
在同圆或等圆中,如果两条劣弧(优弧)、两条两个圆心角中有一组量对应相等,那么它们所对应的其余各组量也分别对应相等.
知识点4点与圆的位置关系
①设点与圆心的距离为,圆的半径为,则点在圆外; 点在圆上; 点在圆内.
②过一点的圆有 个,过两点的圆有 个, 的三点确定一个圆。
过不在同一直线上的三点有且只有一个圆. 这个圆叫做三角形的 ,圆心叫做这个三角形的 ,这个三角形叫做这个圆的 .
二典型例题剖析
题型一 利用垂径定理
例1如图①,已知⊙O的直径AB=16cm,P是OB的中点, ∠APC=30°,求CD的长
【变式训练1】如图②,在△ABC中,∠ACB=90°,AC=12cm,BC=16 cm,以点
C为圆心,AC为半径的圆交斜边AB于点D,求AD的长
题型二 利用圆周角定理求角
例2如图③,C是⊙O的直径AB上一点,以点过点C作弦DE,使CD=CO,若弧AD度数为35°圆心,AC为半径的圆交斜边AB于点D,求弧BE的的度数
【变式训练2】如图④,在⊙O中,弦AC,BD相交于点E,并且弧AB=BC=CD,若∠BEC=130°,求∠ACD的度数
题型三 利用圆周角定理线段
例3如图⑤,△ABC的三个顶点都在⊙O上,若∠C=45°,AB=4,求⊙O的半径
【变式训练3】如图⑥,在直径为2⊙O中有两条弦AB、CD,AB=1,CD=,求弧AB、和CD所对的圆周角的度数
题型四 三角形外接圆
例4如图⑦,在△ABC中,AB=AC=10,BC=12,求△ABC的外接圆的半径
【变式训练4】如果⊙O的半径为1cm,,△ABC为⊙O的内接三角形,且BC=cm,求∠A的度数
跟踪训练
一、填空
1.如图1,M是⊙O内一点,已知过点M的⊙O最长的弦为10 cm,最短的弦长为8 cm,则OM=?_____ cm.?
2.如图2,⊙O的直径AC=2,∠BAD=75°,∠ACD=45°,则四边形ABCD的周长为_____(结果取准确值).
3.如图3,⊙O的直径为10,弦AB=8,P是弦AB上一动点,那么OP长的取值范围是_____.
图1 图2 图3
4.如图4,在⊙O中,两弦AD∥BC,AC、BD相交于点E,连接AB、CD,图中的全等三角形共有_____对.相似比不等于1的相似三角形共有_____对.
5.如图5,在⊙O中,直径AB和弦CD的长分别为10 cm和8 cm,则A、B两点到直线CD的距离之和是_____.
图4 图5
二、选择
6.如图6,点P是半径为5的⊙O内一点,且OP=4,在过P点的所有⊙O的弦中,你认为弦长为整数的弦的条数为
A.6条 B.5条 C.4条 D.2条
7.如图7,在平面直角坐标系中,⊙O′与两坐标分别交于A、B、C、D四点,已知:A(6,0),B(0,-3),C(-2,0),则点D的坐标为
A.(0,2) B.(0,3) C.(0,4) D.(0,5)
图6 图7 图8
8.如图8,已知AB和CD分别是半圆O的直径和弦,AD和BC相交于点E,若∠AEC=α,则
S△CDE∶S△ABE等于
A.sin2α B.cos2α C.tan2α D.与α无关
9.如图9,每张方格纸上都画有一个圆,只用不带刻度的直尺就能确定圆心位置的是
图9
10.如图10,已知:AB=,BC=2,CD=1,∠ABC=45°,则四边形ABCD的面积为
A. B. C. D.
图10
11.如图,现需测量一井盖(圆形)的直径,但只有一把角尺(尺的两边互相垂直,一边有刻度,且两边长度都长于井盖的半径),请配合图形,用文字说明测量方案,写出测量的步骤.(要求写出两种测量方案)
12如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.
(1)P是上一点(不与C、D重合),求证:∠CPD=∠COB.
(2)点P′在劣弧CD上(不与C、D重合)时,∠CP′D与∠COB有什么数量关系?请证明你的结论.
参考答案
一、1. 3 2. 1+2 3. 3≤OP≤5 4. 3 1 5.6 cm
二、6.B 7.C 8.B 9.A 10.D
三、11.方案1:使角尺顶点在圆上,角尺两边与圆两交点连接就是圆的直径,用刻度尺量出直径.
方案2:任画圆的一条弦,用尺量出弦的中点,利用角尺过弦中点做弦的垂线,垂线与圆的两交点间的线段为圆的直径.
12.(1)证明:连结OD, ∵AB是直径,AB⊥CD, ∴=.
∴∠COB=∠DOB=∠COD.
又∵∠CPD=∠COD, ∴∠CPD=∠COB.
(2)略
A
P
O
D
C
B
A
D
C
B
②
A
E
D
C
B
③
A
B
E
C
D
O
④
C
A
B
⑤
A
C
B
D
⑥
A
C
B
⑦⑦
