2020-2021学年苏科版数学七年级下册第十章《二元一次方程组》实际应用常考题专练(二)(Word版 含解析)
文档属性
| 名称 | 2020-2021学年苏科版数学七年级下册第十章《二元一次方程组》实际应用常考题专练(二)(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 98.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 19:30:08 | ||
图片预览




文档简介
2020--2021学年七年级下册第十章《二元一次方程组》
实际应用常考题专练(二)
1.某工厂工人的工作时间为每月25天,每天8小时,该厂生产A、B两种产品.每位工人每月有基本工资400元,工人每生产一件A种产品,可得报酬0.75元,每生产一件B种产品,可得报酬1.40元.下表记录了工人小李的工作情况:
生产A种产品件数
生产B种产品件数
用工时间(分)
1
1
35
3
2
85
(1)小李每生产一件A和B种产品,分别需要多少时间?
(2)求小李每月工资额的范围.
2.某牛奶加工厂现有鲜奶9t,若在市场上直接销售鲜奶,每吨可获利润500元,制成酸奶销售,每吨可获利润1200元,制成奶片销售,每吨可获利2000元.该厂的生产能力是:如制成酸奶,每天可加工3t,制成奶片,每天可加工1t,受人员限制,两种加工方式不可同时进行,受气温限制,这批牛奶需在4天内全部销售或加工完毕,为此,该厂设计了两种方案:
方案一:尽可能多的制成奶片,其余鲜奶直接销售;
方案二:一部分制成奶片,其余制成酸奶销售,并恰好4天完成.
你认为选择哪种方案获利最多,为什么?
3.某工厂从外地连续两次购得A,B两种原料,购买情况如表:现计划租用甲,乙两种货车共8辆将两次购得的原料一次性运回工厂.
A(吨)
B(吨)
费用(元)
第一次
12
8
33600
第二次
8
4
20800
(1)A,B两种原料每吨的进价各是多少元?
(2)已知一辆甲种货车可装4吨A种原料和1吨B种原料;一辆乙种货车可装A,B两种原料各2吨.如何安排甲,乙两种货车?写出所有可行方案.
(3)若甲种货车的运费是每辆400元,乙种货车的运费是每辆350元.设安排甲种货车x辆,总运费为W元,求W(元)与x(辆)之间的函数关系式;在(2)的前提下,x为何值时,总运费W最小,最小值是多少元?
4.某景点的门票价格如下表:
购票人数(人)
1~50
51~99
100以上(含100)
门票单价(元)
48
45
42
(1)某校七年级1、2两个班共有102人去游览该景点,其中1班人数少于50人,2班人数多于50人且少于100人.如果两班都以班为单位单独购票,则一共支付4737元,两个班各有多少名学生?
(2)该校八、九年级自愿报名浏览该景点,其中八年级的报名人数不超过50人,九年级的报名人数超过50人,但不超过80人.若两个年级分别购票,总计支付门票费4914元;若合在一起作为一个团体购票,总计支付门票费4452元,问八年级、九年级各报名多少人?
5.某公司需要粉刷一些相同的房间,经调查3名师傅一天粉刷8个房间,还剩40m2刷不完;5名徒弟一天可以粉刷9个房间;每名师傅比徒弟一天多刷30m2的墙面.
(1)求每个房间需要粉刷的面积;
(2)该公司现有36个这样的房间需要粉刷,若只聘请1名师傅和2名徒弟一起粉刷,需要几天完成?
(3)若来该公司应聘的有3名师傅和10名徒弟,每名师傅和每名徒弟每天的工资分别是240元和200元,该公司要求这36个房间要在2天内粉刷完成,问人工费最低是多少?
6.某景点的门票价格如表:
购票人数(人)
1至50
51至100
100以上
门票的价格(元/人)
12
10
8
学校八年级(1)(2)两个班共102人去该旅游景点游览.其中(1)班人数较少,不到50人.如果两个班都以班级为单位分别购票,则一共应付1118元;如果两个班联合起来作为一个团体购票,则可以省不少钱.
(1)请分别求出两个班各有多少名学生?
(2)两个班联合起来购票能省多少钱?
7.某校七、八年级师生开展“一日游”活动,已知七年级师生共300人,八年级师生共220人.
(1)已知七年级教师比八年级教师多6人,七年级学生比八年级学生多37%,求七年级教师与学生各有多少人;
(2)参观某景点时、需要乘船游玩,现有A、B两种型号的游船,A型船的座位数是B型船的1.5倍,若七年级师生全部乘坐A型船若干艘,刚好坐满,八年级全部乘坐B型船,要比七年级乘坐的A型船多一艘且空20个座位,问:
①A、B两种游船每艘分别有多少个座位;
②若两个年级的师生联合租船,且每艘游船恰好全部坐满,请写出所有的租船方案.
8.某公司在手机网络平台推出的一种新型打车方式受到大众的欢迎.该打车方式的总费用由里程费和耗时费组成,其中里程费按x元/千米计算,耗时费按y元/分钟计算.小聪、小明两人用该打车方式出行,按上述计价规则,他们打车行驶里程数、所用时间及支付车费如下表:
里程数(千米)
时间(分钟)
车费(元)
小聪
3
10
9
小明
6
18
17.4
(1)求x,y的值;
(2)该公司现推出新政策,在原有付费基础上,当里程数超过8千米后,超出的部分要加收0.6元/千米的里程费,小强使用该方式从三水荷花世界打车到大旗头古村,总里程为23千米,耗时30分钟,求小强需支付多少车费.
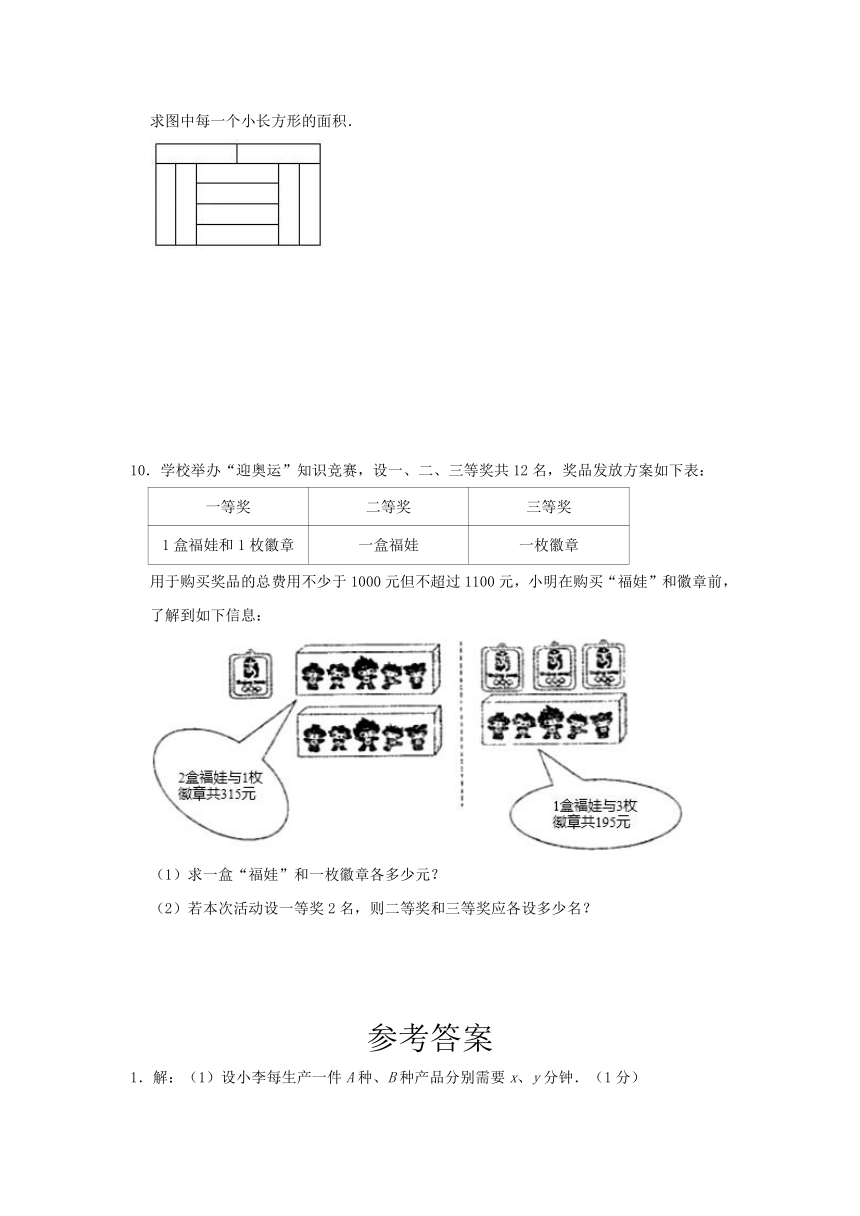
9.如图所示,大长方形图案由10个完全一样的小长方形拼成,若大长方形的短边长为30cm,求图中每一个小长方形的面积.
10.学校举办“迎奥运”知识竞赛,设一、二、三等奖共12名,奖品发放方案如下表:
一等奖
二等奖
三等奖
1盒福娃和1枚徽章
一盒福娃
一枚徽章
用于购买奖品的总费用不少于1000元但不超过1100元,小明在购买“福娃”和徽章前,了解到如下信息:
(1)求一盒“福娃”和一枚徽章各多少元?
(2)若本次活动设一等奖2名,则二等奖和三等奖应各设多少名?
参考答案
1.解:(1)设小李每生产一件A种、B种产品分别需要x、y分钟.(1分)
则,
解得,(3分)
答:小李每生产一件A种和B种产品需要的时间分别为(15分)钟,(20分)钟.(4分)
(2)设小李每月生产A、B两种产品的件数分别为m、n,月工资额为w,(5分)
则,(7分)
即,(8分)
因为m,n为非负整数,所以0≤m≤800,(9分)
故当m=0时,w有最大值为1240,
当m=800时,w有最小值为1000,
∴小李月工资额的范围在1000元至1240元之间(包含1000元,1240元).(10分)
2.解:方案一:4×2000+5×500=10500(元)
方案二:设xt制成奶片,yt制成酸奶,
则,
所以,
利润为1.5×2000+7.5×1200=12000>10500,
所以选择方案二获利最多.
3.解:(1)设A原料每吨的进价是x元;B原料每吨的进价是y元.
则12x+8y=33600;8x+4y=20800
解得x=2000,y=1200
答:A原料每吨的进价是2000元;B原料每吨的进价是1200元.
(2)设甲种货车有a辆.
则4a+2(8﹣a)≥20,a+2(8﹣a)≥12,
解得2≤a≤4
∴可用甲2辆,乙6辆,或甲3辆,乙5辆;或甲4辆,乙4辆.
(3)设总运费为W.
W=400x+350×(8﹣x)=400x+2800﹣350x=50x+2800
∴当x=2时,总运费最小,为2900元.
4.解:(1)设七年级1班有x名学生,2班有y名学生,
由题意得:,
解得:,
答:七年级1班有49名学生,2班有53名学生;
(2)设八年级报名a人,九年级报名b人,
分两种情况:
①若a+b<100,
由题意得:,
解得:,(不合题意舍去);
②若a+b≥100,
由题意得:,
解得:,符合题意;
答:八年级报名48人,九年级报名58人.
5.解:(1)设每个房间需要粉刷的面积为xm2,每名徒弟一天粉刷ym2的墙面,则每名师傅一天粉刷(y+30)m2的墙面,
依题意,得:,
解得:.
答:每个房间需要粉刷的面积为50m2.
(2)由(1)可知:每名徒弟一天粉刷90m2的墙面,每名师傅一天粉刷120m2的墙面,
∴50×36÷(120+90×2)=6(天).
答:需要6天完成.
(3)设聘请m名师傅和n名徒弟完成粉刷任务,
依题意,得:120m+90n=36×50÷2,
∴n=10﹣m.
∵m,n均为非负整数,且0≤m≤3,0≤n≤10,
∴,,
∴该公司共有两种聘请方案,方案1:聘请10名徒弟完成粉刷任务;方案2:聘请3名师傅和6名徒弟完成粉刷任务.
方案1所需人工费为200×10×2=4000(元),
方案2所需人工费为(200×6+240×3)×2=3840(元).
∵4000>3840,
∴方案2聘请3名师傅和6名徒弟完成粉刷任务所需人工费最低,最低人工费为3840元.
6.解:(1)设(1)班有x名学生,(2)班有y名学生,
由题意得:,
解得:.
答:(1)班有49名学生,(2)班有53名学生.
(2)1118﹣8×102=302(元).
答:两个班联合起来购票能省302元.
7.解:(1)设八年级教师有x人,学生有y人,
依题意,得:,
解得:,
∴x+6=26,(1+37%)y=274.
答:七年级教师有26人,学生有274人.
(2)①设B型船每艘有m个座位,则A型船每艘有1.5m个座位,
依题意,得:﹣=1,
解得:m=40,
经检验,m=40是原分式方程的解,且符合题意,
∴1.5m=60.
答:A型船每艘有60个座位,B型船每艘有40个座位.
②设需租用A型船a艘,租用B型船b艘,
依题意,得:60a+40b=300+220,
∴b=13﹣a.
又∵a,b均为非负整数,
∴,,,,,
∴共有5种租船方案,方案1:租用13艘B型船;方案2:租用2艘A型船,10艘B型船;方案3:租用4艘A型船,7艘B型船;方案4:租用6艘A型船,4艘B型船;方案5:租用8艘A型船,1艘B型船.
8.解:(1)根据题意得:,
解得:.
答:x,y的值分别为:2;0.3.
(2)8×2+(23﹣8)×(2+0.6)+30×0.3=64(元).
答:小强需支付64元车费.
9.解:设小长方形的长为x厘米,宽为y厘米,由题意,得
,
解得:,
一个小长方形的面积为:24×6=144.
答:一个小长方形的面积为144cm2.
10.解:(1)设一盒“福娃”x元,一枚徽章y元,
根据题意得
解得.
答:一盒“福娃”150元,一枚徽章15元;
(2)设二等奖m名,则三等奖(10﹣m)名,
解得.
∵m是整数,
∴m=4,∴10﹣m=6
答:二等奖4名,三等奖6名.
实际应用常考题专练(二)
1.某工厂工人的工作时间为每月25天,每天8小时,该厂生产A、B两种产品.每位工人每月有基本工资400元,工人每生产一件A种产品,可得报酬0.75元,每生产一件B种产品,可得报酬1.40元.下表记录了工人小李的工作情况:
生产A种产品件数
生产B种产品件数
用工时间(分)
1
1
35
3
2
85
(1)小李每生产一件A和B种产品,分别需要多少时间?
(2)求小李每月工资额的范围.
2.某牛奶加工厂现有鲜奶9t,若在市场上直接销售鲜奶,每吨可获利润500元,制成酸奶销售,每吨可获利润1200元,制成奶片销售,每吨可获利2000元.该厂的生产能力是:如制成酸奶,每天可加工3t,制成奶片,每天可加工1t,受人员限制,两种加工方式不可同时进行,受气温限制,这批牛奶需在4天内全部销售或加工完毕,为此,该厂设计了两种方案:
方案一:尽可能多的制成奶片,其余鲜奶直接销售;
方案二:一部分制成奶片,其余制成酸奶销售,并恰好4天完成.
你认为选择哪种方案获利最多,为什么?
3.某工厂从外地连续两次购得A,B两种原料,购买情况如表:现计划租用甲,乙两种货车共8辆将两次购得的原料一次性运回工厂.
A(吨)
B(吨)
费用(元)
第一次
12
8
33600
第二次
8
4
20800
(1)A,B两种原料每吨的进价各是多少元?
(2)已知一辆甲种货车可装4吨A种原料和1吨B种原料;一辆乙种货车可装A,B两种原料各2吨.如何安排甲,乙两种货车?写出所有可行方案.
(3)若甲种货车的运费是每辆400元,乙种货车的运费是每辆350元.设安排甲种货车x辆,总运费为W元,求W(元)与x(辆)之间的函数关系式;在(2)的前提下,x为何值时,总运费W最小,最小值是多少元?
4.某景点的门票价格如下表:
购票人数(人)
1~50
51~99
100以上(含100)
门票单价(元)
48
45
42
(1)某校七年级1、2两个班共有102人去游览该景点,其中1班人数少于50人,2班人数多于50人且少于100人.如果两班都以班为单位单独购票,则一共支付4737元,两个班各有多少名学生?
(2)该校八、九年级自愿报名浏览该景点,其中八年级的报名人数不超过50人,九年级的报名人数超过50人,但不超过80人.若两个年级分别购票,总计支付门票费4914元;若合在一起作为一个团体购票,总计支付门票费4452元,问八年级、九年级各报名多少人?
5.某公司需要粉刷一些相同的房间,经调查3名师傅一天粉刷8个房间,还剩40m2刷不完;5名徒弟一天可以粉刷9个房间;每名师傅比徒弟一天多刷30m2的墙面.
(1)求每个房间需要粉刷的面积;
(2)该公司现有36个这样的房间需要粉刷,若只聘请1名师傅和2名徒弟一起粉刷,需要几天完成?
(3)若来该公司应聘的有3名师傅和10名徒弟,每名师傅和每名徒弟每天的工资分别是240元和200元,该公司要求这36个房间要在2天内粉刷完成,问人工费最低是多少?
6.某景点的门票价格如表:
购票人数(人)
1至50
51至100
100以上
门票的价格(元/人)
12
10
8
学校八年级(1)(2)两个班共102人去该旅游景点游览.其中(1)班人数较少,不到50人.如果两个班都以班级为单位分别购票,则一共应付1118元;如果两个班联合起来作为一个团体购票,则可以省不少钱.
(1)请分别求出两个班各有多少名学生?
(2)两个班联合起来购票能省多少钱?
7.某校七、八年级师生开展“一日游”活动,已知七年级师生共300人,八年级师生共220人.
(1)已知七年级教师比八年级教师多6人,七年级学生比八年级学生多37%,求七年级教师与学生各有多少人;
(2)参观某景点时、需要乘船游玩,现有A、B两种型号的游船,A型船的座位数是B型船的1.5倍,若七年级师生全部乘坐A型船若干艘,刚好坐满,八年级全部乘坐B型船,要比七年级乘坐的A型船多一艘且空20个座位,问:
①A、B两种游船每艘分别有多少个座位;
②若两个年级的师生联合租船,且每艘游船恰好全部坐满,请写出所有的租船方案.
8.某公司在手机网络平台推出的一种新型打车方式受到大众的欢迎.该打车方式的总费用由里程费和耗时费组成,其中里程费按x元/千米计算,耗时费按y元/分钟计算.小聪、小明两人用该打车方式出行,按上述计价规则,他们打车行驶里程数、所用时间及支付车费如下表:
里程数(千米)
时间(分钟)
车费(元)
小聪
3
10
9
小明
6
18
17.4
(1)求x,y的值;
(2)该公司现推出新政策,在原有付费基础上,当里程数超过8千米后,超出的部分要加收0.6元/千米的里程费,小强使用该方式从三水荷花世界打车到大旗头古村,总里程为23千米,耗时30分钟,求小强需支付多少车费.
9.如图所示,大长方形图案由10个完全一样的小长方形拼成,若大长方形的短边长为30cm,求图中每一个小长方形的面积.
10.学校举办“迎奥运”知识竞赛,设一、二、三等奖共12名,奖品发放方案如下表:
一等奖
二等奖
三等奖
1盒福娃和1枚徽章
一盒福娃
一枚徽章
用于购买奖品的总费用不少于1000元但不超过1100元,小明在购买“福娃”和徽章前,了解到如下信息:
(1)求一盒“福娃”和一枚徽章各多少元?
(2)若本次活动设一等奖2名,则二等奖和三等奖应各设多少名?
参考答案
1.解:(1)设小李每生产一件A种、B种产品分别需要x、y分钟.(1分)
则,
解得,(3分)
答:小李每生产一件A种和B种产品需要的时间分别为(15分)钟,(20分)钟.(4分)
(2)设小李每月生产A、B两种产品的件数分别为m、n,月工资额为w,(5分)
则,(7分)
即,(8分)
因为m,n为非负整数,所以0≤m≤800,(9分)
故当m=0时,w有最大值为1240,
当m=800时,w有最小值为1000,
∴小李月工资额的范围在1000元至1240元之间(包含1000元,1240元).(10分)
2.解:方案一:4×2000+5×500=10500(元)
方案二:设xt制成奶片,yt制成酸奶,
则,
所以,
利润为1.5×2000+7.5×1200=12000>10500,
所以选择方案二获利最多.
3.解:(1)设A原料每吨的进价是x元;B原料每吨的进价是y元.
则12x+8y=33600;8x+4y=20800
解得x=2000,y=1200
答:A原料每吨的进价是2000元;B原料每吨的进价是1200元.
(2)设甲种货车有a辆.
则4a+2(8﹣a)≥20,a+2(8﹣a)≥12,
解得2≤a≤4
∴可用甲2辆,乙6辆,或甲3辆,乙5辆;或甲4辆,乙4辆.
(3)设总运费为W.
W=400x+350×(8﹣x)=400x+2800﹣350x=50x+2800
∴当x=2时,总运费最小,为2900元.
4.解:(1)设七年级1班有x名学生,2班有y名学生,
由题意得:,
解得:,
答:七年级1班有49名学生,2班有53名学生;
(2)设八年级报名a人,九年级报名b人,
分两种情况:
①若a+b<100,
由题意得:,
解得:,(不合题意舍去);
②若a+b≥100,
由题意得:,
解得:,符合题意;
答:八年级报名48人,九年级报名58人.
5.解:(1)设每个房间需要粉刷的面积为xm2,每名徒弟一天粉刷ym2的墙面,则每名师傅一天粉刷(y+30)m2的墙面,
依题意,得:,
解得:.
答:每个房间需要粉刷的面积为50m2.
(2)由(1)可知:每名徒弟一天粉刷90m2的墙面,每名师傅一天粉刷120m2的墙面,
∴50×36÷(120+90×2)=6(天).
答:需要6天完成.
(3)设聘请m名师傅和n名徒弟完成粉刷任务,
依题意,得:120m+90n=36×50÷2,
∴n=10﹣m.
∵m,n均为非负整数,且0≤m≤3,0≤n≤10,
∴,,
∴该公司共有两种聘请方案,方案1:聘请10名徒弟完成粉刷任务;方案2:聘请3名师傅和6名徒弟完成粉刷任务.
方案1所需人工费为200×10×2=4000(元),
方案2所需人工费为(200×6+240×3)×2=3840(元).
∵4000>3840,
∴方案2聘请3名师傅和6名徒弟完成粉刷任务所需人工费最低,最低人工费为3840元.
6.解:(1)设(1)班有x名学生,(2)班有y名学生,
由题意得:,
解得:.
答:(1)班有49名学生,(2)班有53名学生.
(2)1118﹣8×102=302(元).
答:两个班联合起来购票能省302元.
7.解:(1)设八年级教师有x人,学生有y人,
依题意,得:,
解得:,
∴x+6=26,(1+37%)y=274.
答:七年级教师有26人,学生有274人.
(2)①设B型船每艘有m个座位,则A型船每艘有1.5m个座位,
依题意,得:﹣=1,
解得:m=40,
经检验,m=40是原分式方程的解,且符合题意,
∴1.5m=60.
答:A型船每艘有60个座位,B型船每艘有40个座位.
②设需租用A型船a艘,租用B型船b艘,
依题意,得:60a+40b=300+220,
∴b=13﹣a.
又∵a,b均为非负整数,
∴,,,,,
∴共有5种租船方案,方案1:租用13艘B型船;方案2:租用2艘A型船,10艘B型船;方案3:租用4艘A型船,7艘B型船;方案4:租用6艘A型船,4艘B型船;方案5:租用8艘A型船,1艘B型船.
8.解:(1)根据题意得:,
解得:.
答:x,y的值分别为:2;0.3.
(2)8×2+(23﹣8)×(2+0.6)+30×0.3=64(元).
答:小强需支付64元车费.
9.解:设小长方形的长为x厘米,宽为y厘米,由题意,得
,
解得:,
一个小长方形的面积为:24×6=144.
答:一个小长方形的面积为144cm2.
10.解:(1)设一盒“福娃”x元,一枚徽章y元,
根据题意得
解得.
答:一盒“福娃”150元,一枚徽章15元;
(2)设二等奖m名,则三等奖(10﹣m)名,
解得.
∵m是整数,
∴m=4,∴10﹣m=6
答:二等奖4名,三等奖6名.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
