8.3 统计分析帮你做预测 课件(共29张PPT)
文档属性
| 名称 | 8.3 统计分析帮你做预测 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 00:00:00 | ||
图片预览





文档简介
8.3 统计分析帮你做预测
2020-2021学年度苏科版九年级下册
第8章 统计和概率的简单应用
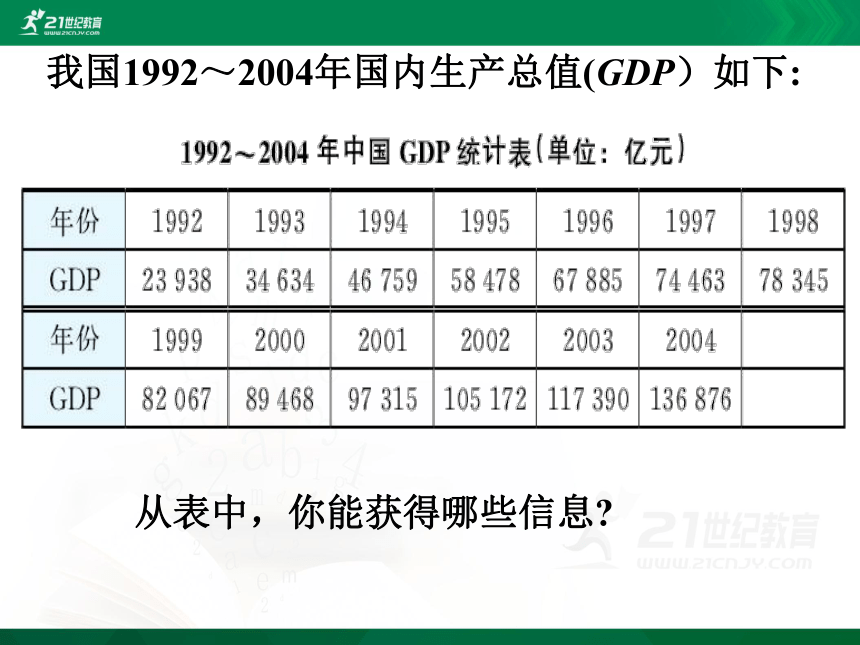
我国1992~2004年国内生产总值(GDP)如下:
从表中,你能获得哪些信息?
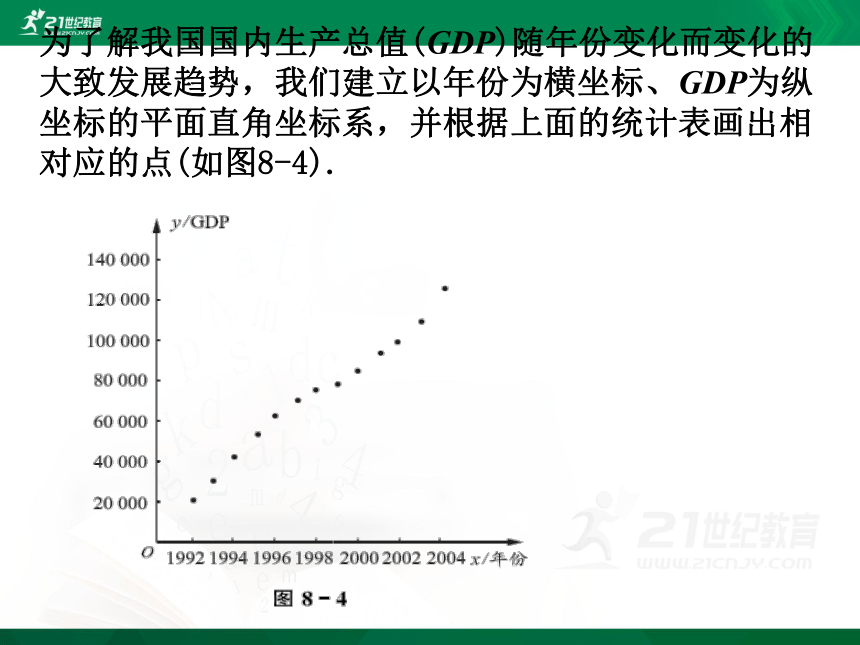
为了解我国国内生产总值(GDP)随年份变化而变化的大致发展趋势,我们建立以年份为横坐标、GDP为纵坐标的平面直角坐标系,并根据上面的统计表画出相对应的点(如图8-4).
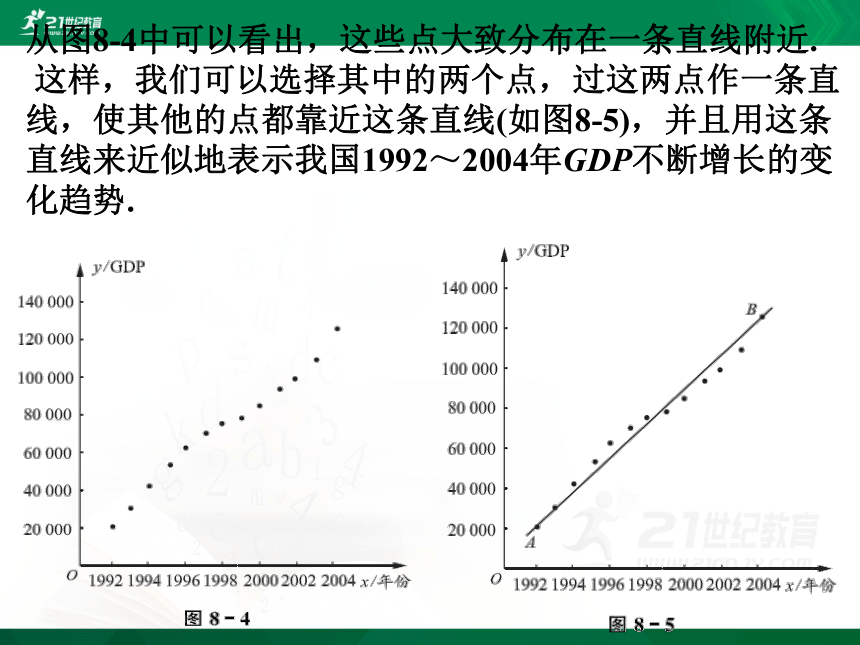
从图8-4中可以看出,这些点大致分布在一条直线附近.
这样,我们可以选择其中的两个点,过这两点作一条直线,使其他的点都靠近这条直线(如图8-5),并且用这条直线来近似地表示我国1992~2004年GDP不断增长的变化趋势.
设直线AB上点的坐标满足函数表达式y = kx + b.
由直线AB过点(1992,23 938), (2004,136 876),
可得方程组
解得k = 9 411. 5,b=-18 723 770.
于是,可以近似地得到1992~2004年我国GDP与年份之间的函数表达式为y = 9 411. 5x-18 723 770.
按照我国1992~2004年GDP不断增长的变化趋势,由这个表达式可以估计2005年我国的GDP.
还可以选用其他的直线来近似地表示我国1992~2004年GDP随年份变化而变化的大致发展趋势吗?
在日常生活中,类似这样的例子还很多.例如,学生的身高和体重之间,同一种树的树叶长与宽之间等,都存在着某种数量关系.你不妨做一些调查,探索其内在的数量关系.
P(A)=
m
n
在数学中,我们把事件发生的可能性的大小
称为事件发生的概率
如果事件发生的各种可能结果的可能性相同,
事件A发生的可能的结果总数为m.
结果总数为n
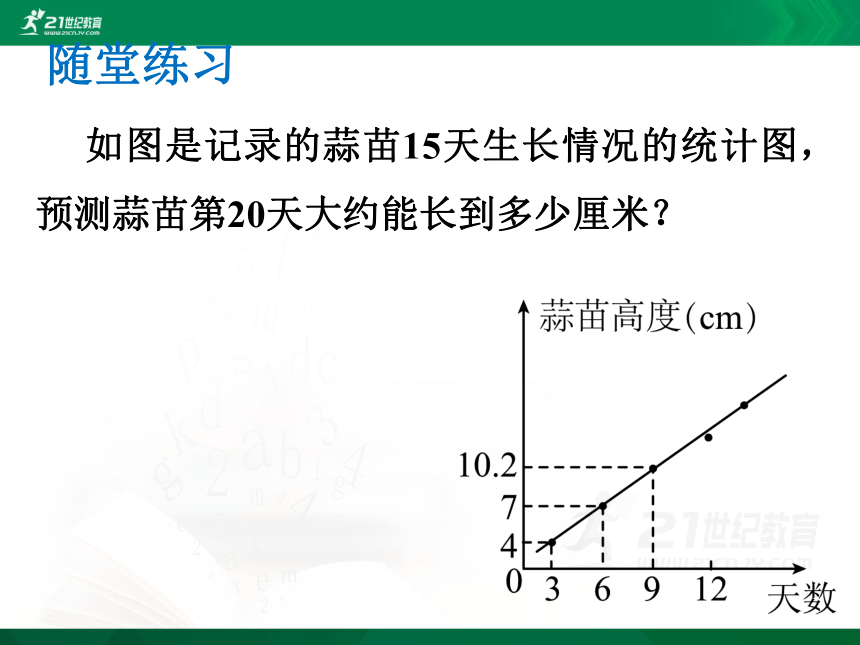
如图是记录的蒜苗15天生长情况的统计图,预测蒜苗第20天大约能长到多少厘米?
随堂练习
[解析] 折线图可近似看作是直线,设直线所对应的函数表达式为y=kx+b,把点(3,4),(6,7)代入表达式求出k,b的值,再即可.
[答案] 解得k=1,b=1,所以y=x+1,把x=20代入可得y=21.
课外练习
1.经过大量试验统计,香樟树在我区的移植的成活率为95%.
(1)顺河镇在新村建设中栽了4000株香樟树,则成活的香樟树大约是________株.
(2)建淮镇在新村建设中要栽活2850株香樟树,需购幼树______株.
2.一个口袋中放有20个球,其中红球6个,白球和黑球个若干个,每个球出了颜色外没有任何区别.
(1)小王通过大量反复实验(每次取一个球,放回搅匀后再取)发现,取出黑球的概率稳定在1/4左右,请你估计袋中黑球的个数.
(2)若小王取出的第一个是白球,将它放在桌上,从袋中余下的球中在再任意取一个球,取出红球的概率是多少?
射击次数n
10
20
50
100
200
500
击中靶心次数m
8
19
44
92
178
452
击中靶心频率m/n
(1)计算表中击中靶心的各个频率并填入表中.
(2)这个运动员射击一次,击中靶心的概率约是 _____.
3.某射击运动员在同一条件下练习射击,结果如下表所示:
某弹簧的自然长度为3cm,在弹性限度内所挂的物体的重量x 每增加1 kg ,弹簧长度y增加0.5cm.
x/kg
1
2
3
4
5
……
y/cm
……
依据上表数据,写出y与x之间的关系式.
3.5
y = 3+0.5x
4
4.5
5
5.5
1kg
2kg
3kg
我国1992~2004年国内生产总值(GDP)如下:
思考与探索:
从表中,你能获得哪些信息?
我们建立以年份为横坐标,GDP为纵坐标的平面直角坐标系,并根据上面的统计表画出相对应的点:
操作与观察:
观察这些点的分布,你有什么发现?
我们建立以年份为横坐标,GDP为纵坐标的平面直角坐标系,并根据上面的统计表画出相对应的点.
你能选择其中的两点确定一条直线,使其他的点都靠近这条直线吗?
这些点大致分布在一条直线附近!
操作与观察:
计算与思考:
你能由此表达式估计我国2004年以后的GDP情况吗?
设直线AB上点的坐标满足函数表达式y=kx+b.
由直线AB过点(1992,23 938)、(2004,136 876),可得方程组:
解得k=9 411.5,b=-18 723 770.
y=9 411.5x-18 723 770.
在刚才的问题中,还可以选用其他的直线来近似的表示我国1992~2004年GDP随年份变化而变化的大致发展趋势吗?
思考:
1.袋中装有白球和红球共20个,每个球除颜色外都相同,袋中有多少个白球、多少个红球呢?
我们通过摸球试验来估计:
你的估计与实际一致吗?为什么?
随堂练习:
2.随机调查了某校10名九年级男生的身高和体重,整理如下:
(1)以体重为横坐标,身高为纵坐标,在平面直角坐标系中画出相对应的点,并选用一条适当的直线近似表示这10名男生身高与体重之间的变化趋势;
(2)求这10名男生身高与体重之间关系的近似表达式,并由这个表达式估计该校身高180cm的九年级男生的体重情况.
身高/cm
164
166
168
170
172
174
176
178
180
182
184
体重/kg
45
50
55
60
65
70
●
●
●
●
●
●
●
●
●
●
(1)
(2)设直线所对应的函数表达式为y=kx+b,把点(43,165),(69,183)代入表达式求出k,b的值.
当y=180,x=64.8.
二、用概率作估计
在研究工作中,生态学家经常要确定生物种群的数量,由于生物种群可能数量很多,或者分布很广,很难找到所有的生物个体.
这时,他们往往利用“生物取样”的方法来估计种群的数量.
生物取样,就是在一个小区域内统计生物种群的数量(一个样本),假设这个样本与较大区域是有相同的生物种群密度,统计这个小区域内的生物种群数量,然后在乘以相应的倍数,即可确定一个较大区域的生物种群的数量.
为了估计湖里有多少条鱼,先从湖里捕捞100条鱼做上标记,然后再放回湖里去,经过一段时间,待有标记的鱼完全混同与鱼群后,第二次再捕捞200条鱼,若其中25条有标记,那么请你估计湖里大约有多少条鱼?
这种用有限估计无限的方法叫做“标记再捕获研究法”.
一个口袋中有10个红球和若干个白球,请通过以下实验估计口袋中白球的个数:从口袋中随机摸出一球,记下其颜色,再把它放回口袋中,不断重复上述过程.实验中总共摸了200次,其中有50次摸到红球.
解法一:
设口袋中有x个白球,
由题意得,
解得x=30.
答:口袋中约有30个白球.
解法二:
∵P(50次摸到红球)=
∴10÷ =40 .∴ 40-10=30 .
答:口袋中大约有30个白球.
随堂练习:
小结:
在随机实验中,每一次实验的结果事先是无法预料到的,收集到的实验数据都带有不确定性,但经过大量的实验后,频率会稳定在理论概率上,因而我们可以用实验得到的频率来估计概率.
谢谢聆听
2020-2021学年度苏科版九年级下册
第8章 统计和概率的简单应用
我国1992~2004年国内生产总值(GDP)如下:
从表中,你能获得哪些信息?
为了解我国国内生产总值(GDP)随年份变化而变化的大致发展趋势,我们建立以年份为横坐标、GDP为纵坐标的平面直角坐标系,并根据上面的统计表画出相对应的点(如图8-4).
从图8-4中可以看出,这些点大致分布在一条直线附近.
这样,我们可以选择其中的两个点,过这两点作一条直线,使其他的点都靠近这条直线(如图8-5),并且用这条直线来近似地表示我国1992~2004年GDP不断增长的变化趋势.
设直线AB上点的坐标满足函数表达式y = kx + b.
由直线AB过点(1992,23 938), (2004,136 876),
可得方程组
解得k = 9 411. 5,b=-18 723 770.
于是,可以近似地得到1992~2004年我国GDP与年份之间的函数表达式为y = 9 411. 5x-18 723 770.
按照我国1992~2004年GDP不断增长的变化趋势,由这个表达式可以估计2005年我国的GDP.
还可以选用其他的直线来近似地表示我国1992~2004年GDP随年份变化而变化的大致发展趋势吗?
在日常生活中,类似这样的例子还很多.例如,学生的身高和体重之间,同一种树的树叶长与宽之间等,都存在着某种数量关系.你不妨做一些调查,探索其内在的数量关系.
P(A)=
m
n
在数学中,我们把事件发生的可能性的大小
称为事件发生的概率
如果事件发生的各种可能结果的可能性相同,
事件A发生的可能的结果总数为m.
结果总数为n
如图是记录的蒜苗15天生长情况的统计图,预测蒜苗第20天大约能长到多少厘米?
随堂练习
[解析] 折线图可近似看作是直线,设直线所对应的函数表达式为y=kx+b,把点(3,4),(6,7)代入表达式求出k,b的值,再即可.
[答案] 解得k=1,b=1,所以y=x+1,把x=20代入可得y=21.
课外练习
1.经过大量试验统计,香樟树在我区的移植的成活率为95%.
(1)顺河镇在新村建设中栽了4000株香樟树,则成活的香樟树大约是________株.
(2)建淮镇在新村建设中要栽活2850株香樟树,需购幼树______株.
2.一个口袋中放有20个球,其中红球6个,白球和黑球个若干个,每个球出了颜色外没有任何区别.
(1)小王通过大量反复实验(每次取一个球,放回搅匀后再取)发现,取出黑球的概率稳定在1/4左右,请你估计袋中黑球的个数.
(2)若小王取出的第一个是白球,将它放在桌上,从袋中余下的球中在再任意取一个球,取出红球的概率是多少?
射击次数n
10
20
50
100
200
500
击中靶心次数m
8
19
44
92
178
452
击中靶心频率m/n
(1)计算表中击中靶心的各个频率并填入表中.
(2)这个运动员射击一次,击中靶心的概率约是 _____.
3.某射击运动员在同一条件下练习射击,结果如下表所示:
某弹簧的自然长度为3cm,在弹性限度内所挂的物体的重量x 每增加1 kg ,弹簧长度y增加0.5cm.
x/kg
1
2
3
4
5
……
y/cm
……
依据上表数据,写出y与x之间的关系式.
3.5
y = 3+0.5x
4
4.5
5
5.5
1kg
2kg
3kg
我国1992~2004年国内生产总值(GDP)如下:
思考与探索:
从表中,你能获得哪些信息?
我们建立以年份为横坐标,GDP为纵坐标的平面直角坐标系,并根据上面的统计表画出相对应的点:
操作与观察:
观察这些点的分布,你有什么发现?
我们建立以年份为横坐标,GDP为纵坐标的平面直角坐标系,并根据上面的统计表画出相对应的点.
你能选择其中的两点确定一条直线,使其他的点都靠近这条直线吗?
这些点大致分布在一条直线附近!
操作与观察:
计算与思考:
你能由此表达式估计我国2004年以后的GDP情况吗?
设直线AB上点的坐标满足函数表达式y=kx+b.
由直线AB过点(1992,23 938)、(2004,136 876),可得方程组:
解得k=9 411.5,b=-18 723 770.
y=9 411.5x-18 723 770.
在刚才的问题中,还可以选用其他的直线来近似的表示我国1992~2004年GDP随年份变化而变化的大致发展趋势吗?
思考:
1.袋中装有白球和红球共20个,每个球除颜色外都相同,袋中有多少个白球、多少个红球呢?
我们通过摸球试验来估计:
你的估计与实际一致吗?为什么?
随堂练习:
2.随机调查了某校10名九年级男生的身高和体重,整理如下:
(1)以体重为横坐标,身高为纵坐标,在平面直角坐标系中画出相对应的点,并选用一条适当的直线近似表示这10名男生身高与体重之间的变化趋势;
(2)求这10名男生身高与体重之间关系的近似表达式,并由这个表达式估计该校身高180cm的九年级男生的体重情况.
身高/cm
164
166
168
170
172
174
176
178
180
182
184
体重/kg
45
50
55
60
65
70
●
●
●
●
●
●
●
●
●
●
(1)
(2)设直线所对应的函数表达式为y=kx+b,把点(43,165),(69,183)代入表达式求出k,b的值.
当y=180,x=64.8.
二、用概率作估计
在研究工作中,生态学家经常要确定生物种群的数量,由于生物种群可能数量很多,或者分布很广,很难找到所有的生物个体.
这时,他们往往利用“生物取样”的方法来估计种群的数量.
生物取样,就是在一个小区域内统计生物种群的数量(一个样本),假设这个样本与较大区域是有相同的生物种群密度,统计这个小区域内的生物种群数量,然后在乘以相应的倍数,即可确定一个较大区域的生物种群的数量.
为了估计湖里有多少条鱼,先从湖里捕捞100条鱼做上标记,然后再放回湖里去,经过一段时间,待有标记的鱼完全混同与鱼群后,第二次再捕捞200条鱼,若其中25条有标记,那么请你估计湖里大约有多少条鱼?
这种用有限估计无限的方法叫做“标记再捕获研究法”.
一个口袋中有10个红球和若干个白球,请通过以下实验估计口袋中白球的个数:从口袋中随机摸出一球,记下其颜色,再把它放回口袋中,不断重复上述过程.实验中总共摸了200次,其中有50次摸到红球.
解法一:
设口袋中有x个白球,
由题意得,
解得x=30.
答:口袋中约有30个白球.
解法二:
∵P(50次摸到红球)=
∴10÷ =40 .∴ 40-10=30 .
答:口袋中大约有30个白球.
随堂练习:
小结:
在随机实验中,每一次实验的结果事先是无法预料到的,收集到的实验数据都带有不确定性,但经过大量的实验后,频率会稳定在理论概率上,因而我们可以用实验得到的频率来估计概率.
谢谢聆听
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
