8.4 抽签方法合理吗 课件(共24张PPT)
文档属性
| 名称 | 8.4 抽签方法合理吗 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 00:00:00 | ||
图片预览








文档简介
8.4 抽签方法合理吗
2020-2021学年度苏科版九年级下册
第8章 统计和概率的简单应用
等可能条件下的概率的计算方法:
其中m表示事件A发生可能出现的结果数,n表示一次试验所有等可能出现的结果数
我们所研究的事件大都是随机事件。所以其概率在0和1之间。
说明:
相关知识回顾
小明和小丽轮流向一小圆形桌面上放一元硬币,硬币不重叠;直至圆形桌面里不能再放入为止,谁放入圆形桌面上最后一个,谁就获胜,这个游戏公平吗?
情境
由圆的中心对称性,可知圆形桌面最多能放奇数个硬币,所以先放的人一定会赢.
谁先放呢?请你帮出个主意.
一、创设情境:
问题一:有一张电影票,小明和小丽用抽签的方法来决定谁可以去看电影,于是准备了两张相同的小纸条,一张上面是“去”,另一张上面是“不去”,谁抽到“去”,则这个人就去看电影,这种方法公平吗?
问题二:我们用抽签的方法从3名同学中选一名去参加某音乐会。事先准备三张相同的小纸条,并在1张纸条画上记号,其余2张纸条不画。把3张纸条放在一个盒子中搅匀,然后让3名同学去摸纸条,这种方法公平吗?
先抽的人中签的可能性大一些,后抽的人可能吃亏
如果先抽的人没有抽到,那么后抽的人中签的可能性不就大了吗?
二、提出质疑:
抽签有先有后,如果先抽的人抽到了,后抽的人就抽不到了.可是,如果先抽的人没有抽到,后抽的人抽到的机会就大了?先抽的人与后抽的人中签的概率一样吗?
学生探索:
下面我们就来算一算各人中签的概率:
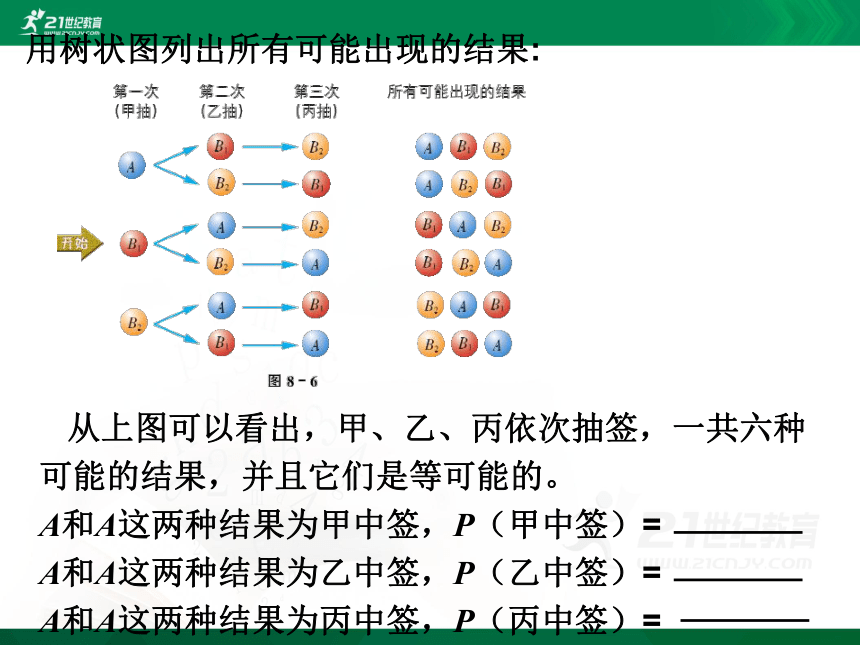
假设这3名同学分别记作甲、乙、丙,他们抽签的顺序依次为:甲第一,乙第二,丙第三.三张小纸条中,画有记号的纸条记作A,余下的两张没有记号的纸条分别记作和.
用树状图列出所有可能出现的结果:
从上图可以看出,甲、乙、丙依次抽签,一共六种可能的结果,并且它们是等可能的。
A和A这两种结果为甲中签,P(甲中签)=
A和A这两种结果为乙中签,P(乙中签)=
A和A这两种结果为丙中签,P(丙中签)=
(1)因为甲先抽,中签的概率是:
则它不中签的概率是:
(2)接着抽签的乙只有在甲不中的情 况下才有可能中签,此时它中签的概
率是:
(3)最后抽签的丙中签的概率是:
三、总结:
通过上面的分析我们看到,抽签虽然有先有后,但是先抽的人和后抽的人中签的可能性是 的,因此对每个人来说都是 的,所以不必挣着先抽签.
抽签的方法是合理的
相同
公平
四、课堂练习:
1.用抽签的方法从三名同学种选两名去看电影.这种方法公平吗?请说明理由.
2.小明和小丽两人各掷一枚骰子,如果两枚骰子的点数之和是奇数,小明得一分,否则小丽的一分,谁先得十分,谁就得胜.这个游戏对双方公平吗?(游戏对双方公平是指双方获胜的概率相等)
3.一只不透明的袋子中装有2个白球和2个红球,这些球除颜色外都相同,搅匀后甲、乙、丙3人依次按顺序从中任意摸出1个球(摸出的球不放回).求丙摸到白球的概率?
4.有A、B、C、D、4部不同的电影,甲、乙2人分别从中任意选择1部观看.求甲、乙2人选择同1部电影的概率.
解:画树状图得:
共有16种可能的结果,甲、乙两人选择同一部电影的有4种情况
∴甲、乙2人选择同1部电影的概率为:
A
A
B
C
D
B
A
B
C
D
C
A
B
C
D
D
A
B
C
D
甲
乙
回顾:
1.一定会发生的事件叫________事件;一定不会发生的事件叫_________事件;它们通称_________事件;无法确定是否会发生的事件叫_______事件.
2.无论是试验的所有可能产生结果是有限个,还是无限个,具备哪几个特征的试验结果才具有等可能性? ①在试验中发生的事件都是______事件;
②在每一次试验中有且只有_ 个结果出现;
③每个结果出现机会___________.
3.等可能条件下的概率的计算方法是什么?
情境
一张门票,三人选一人,怎么办?
抽签
这个游戏公平吗?
用抽签的方法从三名同学中选一名去出席某场音乐会,事先准备三张相同的纸条,并在一张纸条上画上记号,其余2张不画.把三张纸条放在一个盒子中摇匀,然后让三名同学去摸纸条,摸到有标记的纸条的那位同学将被选中.
抽签有先有后,先抽的人和后抽的人中签的概率一样吗?
探索一:
可以运用概率知识判断先抽的人与后抽的人中签的概率是否相同.
小组活动:
1.请求出3名同学抽中的概率
假设甲、乙、丙3名学生抽签的顺序依次为:甲第一,乙第二,丙第三;3张纸条中,画有记号的纸条记做A,其余2张纸条分别记做B1和B2.
你认为此种抽签方法合理吗?为什么?
思考:
若用抽签的办法从3名同学中选两名去参加音乐会,这种方法公平吗?
1.袋中有5个白球,n个红球,从中任意取一个球,恰好红球的概率为 ,则n=_____.
2.一个均匀的立方体六个面上分别标有数1,2,3,4,5,6.右图是这个立方体表面的展开图.抛掷这个立方体,则朝上一面上的数恰好等于朝下一面上的数的 的概率是( )
A、 B、
C、 D、
做一做
10
A
3
5
4
6
1
2
2.小明和小丽两人各掷一枚骰子,如果两枚骰子的点数之和是奇数,小明得一分,否则小丽得一分,谁先得十分,谁就得胜.这个游戏对双方公平吗?(游戏对双方公平是指双方获胜的概率相等)
探索二:
课外练习
1.一张圆桌旁有四个座位,A先坐在1号座位上,B、C、D三人随机做到其他三个位置上.求A与B不相邻而坐的概率.
2、学校门口经常有小贩搞摸奖活动.某小贩在一只黑色的口袋里装有只有颜色不同的50只小球,其中红球1只,黄球2只,绿球10只,其余为白球.搅拌均匀后,每2元摸1个球.奖品分为8元、5元、1元、无.
(1)如果花2元摸1个球,那么摸不到奖的概率是多少?
(2)如果花4元同时摸到2个球,那么获得10元奖品的概率是多少?
3.一只不透明的袋子中装有2个白球和2个红球,这些球除颜色外都相同,搅匀后甲、乙、丙3人依次按顺序从中任意摸出1个球(摸出的球不放回).求丙摸到白球的概率.
白
红
白
红
红
红
白
红
白
红
白
白
红
红
红
白
红
白
甲
乙
丙
白
白
解:画树状图得:
∴丙摸到白球的概率为:
小结:
P(A)=
m
n
1、等可能条件下的概率的计算方法:
其中:
m表示事件A发生可能出现的结果数,
n表示一次试验所有等可能出现的结果数.
2、求所有等可能出现的结果数的方法是:
画树状图或者列表格
谢谢聆听
2020-2021学年度苏科版九年级下册
第8章 统计和概率的简单应用
等可能条件下的概率的计算方法:
其中m表示事件A发生可能出现的结果数,n表示一次试验所有等可能出现的结果数
我们所研究的事件大都是随机事件。所以其概率在0和1之间。
说明:
相关知识回顾
小明和小丽轮流向一小圆形桌面上放一元硬币,硬币不重叠;直至圆形桌面里不能再放入为止,谁放入圆形桌面上最后一个,谁就获胜,这个游戏公平吗?
情境
由圆的中心对称性,可知圆形桌面最多能放奇数个硬币,所以先放的人一定会赢.
谁先放呢?请你帮出个主意.
一、创设情境:
问题一:有一张电影票,小明和小丽用抽签的方法来决定谁可以去看电影,于是准备了两张相同的小纸条,一张上面是“去”,另一张上面是“不去”,谁抽到“去”,则这个人就去看电影,这种方法公平吗?
问题二:我们用抽签的方法从3名同学中选一名去参加某音乐会。事先准备三张相同的小纸条,并在1张纸条画上记号,其余2张纸条不画。把3张纸条放在一个盒子中搅匀,然后让3名同学去摸纸条,这种方法公平吗?
先抽的人中签的可能性大一些,后抽的人可能吃亏
如果先抽的人没有抽到,那么后抽的人中签的可能性不就大了吗?
二、提出质疑:
抽签有先有后,如果先抽的人抽到了,后抽的人就抽不到了.可是,如果先抽的人没有抽到,后抽的人抽到的机会就大了?先抽的人与后抽的人中签的概率一样吗?
学生探索:
下面我们就来算一算各人中签的概率:
假设这3名同学分别记作甲、乙、丙,他们抽签的顺序依次为:甲第一,乙第二,丙第三.三张小纸条中,画有记号的纸条记作A,余下的两张没有记号的纸条分别记作和.
用树状图列出所有可能出现的结果:
从上图可以看出,甲、乙、丙依次抽签,一共六种可能的结果,并且它们是等可能的。
A和A这两种结果为甲中签,P(甲中签)=
A和A这两种结果为乙中签,P(乙中签)=
A和A这两种结果为丙中签,P(丙中签)=
(1)因为甲先抽,中签的概率是:
则它不中签的概率是:
(2)接着抽签的乙只有在甲不中的情 况下才有可能中签,此时它中签的概
率是:
(3)最后抽签的丙中签的概率是:
三、总结:
通过上面的分析我们看到,抽签虽然有先有后,但是先抽的人和后抽的人中签的可能性是 的,因此对每个人来说都是 的,所以不必挣着先抽签.
抽签的方法是合理的
相同
公平
四、课堂练习:
1.用抽签的方法从三名同学种选两名去看电影.这种方法公平吗?请说明理由.
2.小明和小丽两人各掷一枚骰子,如果两枚骰子的点数之和是奇数,小明得一分,否则小丽的一分,谁先得十分,谁就得胜.这个游戏对双方公平吗?(游戏对双方公平是指双方获胜的概率相等)
3.一只不透明的袋子中装有2个白球和2个红球,这些球除颜色外都相同,搅匀后甲、乙、丙3人依次按顺序从中任意摸出1个球(摸出的球不放回).求丙摸到白球的概率?
4.有A、B、C、D、4部不同的电影,甲、乙2人分别从中任意选择1部观看.求甲、乙2人选择同1部电影的概率.
解:画树状图得:
共有16种可能的结果,甲、乙两人选择同一部电影的有4种情况
∴甲、乙2人选择同1部电影的概率为:
A
A
B
C
D
B
A
B
C
D
C
A
B
C
D
D
A
B
C
D
甲
乙
回顾:
1.一定会发生的事件叫________事件;一定不会发生的事件叫_________事件;它们通称_________事件;无法确定是否会发生的事件叫_______事件.
2.无论是试验的所有可能产生结果是有限个,还是无限个,具备哪几个特征的试验结果才具有等可能性? ①在试验中发生的事件都是______事件;
②在每一次试验中有且只有_ 个结果出现;
③每个结果出现机会___________.
3.等可能条件下的概率的计算方法是什么?
情境
一张门票,三人选一人,怎么办?
抽签
这个游戏公平吗?
用抽签的方法从三名同学中选一名去出席某场音乐会,事先准备三张相同的纸条,并在一张纸条上画上记号,其余2张不画.把三张纸条放在一个盒子中摇匀,然后让三名同学去摸纸条,摸到有标记的纸条的那位同学将被选中.
抽签有先有后,先抽的人和后抽的人中签的概率一样吗?
探索一:
可以运用概率知识判断先抽的人与后抽的人中签的概率是否相同.
小组活动:
1.请求出3名同学抽中的概率
假设甲、乙、丙3名学生抽签的顺序依次为:甲第一,乙第二,丙第三;3张纸条中,画有记号的纸条记做A,其余2张纸条分别记做B1和B2.
你认为此种抽签方法合理吗?为什么?
思考:
若用抽签的办法从3名同学中选两名去参加音乐会,这种方法公平吗?
1.袋中有5个白球,n个红球,从中任意取一个球,恰好红球的概率为 ,则n=_____.
2.一个均匀的立方体六个面上分别标有数1,2,3,4,5,6.右图是这个立方体表面的展开图.抛掷这个立方体,则朝上一面上的数恰好等于朝下一面上的数的 的概率是( )
A、 B、
C、 D、
做一做
10
A
3
5
4
6
1
2
2.小明和小丽两人各掷一枚骰子,如果两枚骰子的点数之和是奇数,小明得一分,否则小丽得一分,谁先得十分,谁就得胜.这个游戏对双方公平吗?(游戏对双方公平是指双方获胜的概率相等)
探索二:
课外练习
1.一张圆桌旁有四个座位,A先坐在1号座位上,B、C、D三人随机做到其他三个位置上.求A与B不相邻而坐的概率.
2、学校门口经常有小贩搞摸奖活动.某小贩在一只黑色的口袋里装有只有颜色不同的50只小球,其中红球1只,黄球2只,绿球10只,其余为白球.搅拌均匀后,每2元摸1个球.奖品分为8元、5元、1元、无.
(1)如果花2元摸1个球,那么摸不到奖的概率是多少?
(2)如果花4元同时摸到2个球,那么获得10元奖品的概率是多少?
3.一只不透明的袋子中装有2个白球和2个红球,这些球除颜色外都相同,搅匀后甲、乙、丙3人依次按顺序从中任意摸出1个球(摸出的球不放回).求丙摸到白球的概率.
白
红
白
红
红
红
白
红
白
红
白
白
红
红
红
白
红
白
甲
乙
丙
白
白
解:画树状图得:
∴丙摸到白球的概率为:
小结:
P(A)=
m
n
1、等可能条件下的概率的计算方法:
其中:
m表示事件A发生可能出现的结果数,
n表示一次试验所有等可能出现的结果数.
2、求所有等可能出现的结果数的方法是:
画树状图或者列表格
谢谢聆听
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
