8.5 概率帮你做估计 课件(共32张PPT)
文档属性
| 名称 | 8.5 概率帮你做估计 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 18:35:54 | ||
图片预览











文档简介
8.5 概率帮你做估计
2020-2021学年度苏科版九年级下册
第8章 统计和概率的简单应用
频数:
在考察中,每个对象出现的次数称为频数
频率:
而每个对象出现的次数与总次数的比值称为频率.
概率:
概念回顾
P(A)=
m
n
在数学中,我们把事件发生的可能性的大小
称为事件发生的概率
如果事件发生的每种可能结果的可能性相同,
事件A发生的可能的结果总数为m
结果总数为n
概念回顾
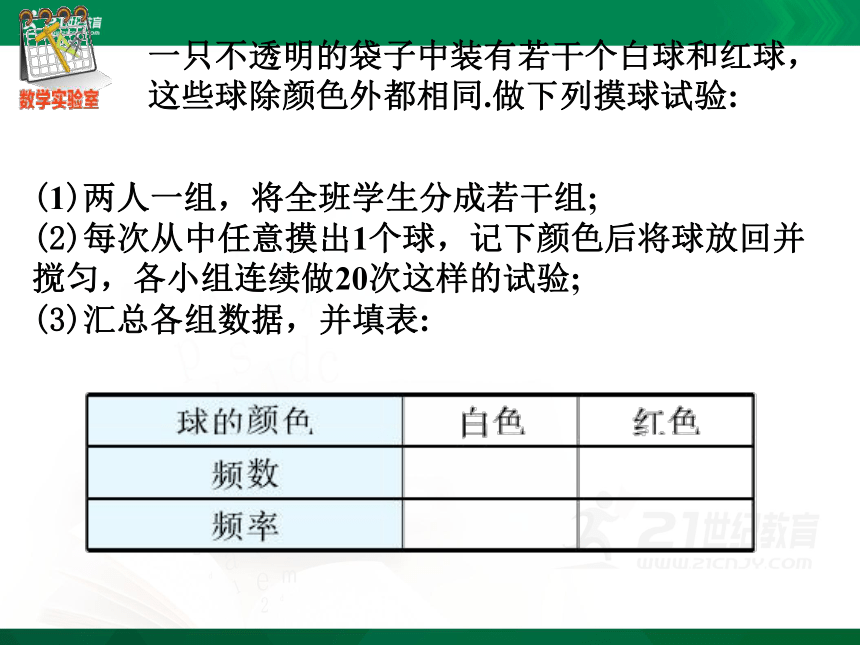
一只不透明的袋子中装有若干个白球和红球,这些球除颜色外都相同.做下列摸球试验:
(1)两人一组,将全班学生分成若干组;
(2)每次从中任意摸出1个球,记下颜色后将球放回并搅匀,各小组连续做20次这样的试验;
(3)汇总各组数据,并填表:
根据试验的结果,你能估计袋子中白球数与红球数的比吗?
假设全班一共做了400次这样的摸球试验,摸到白球的频数为40且已知袋中有白球5个,你能估计袋中红球的个数吗?
由400次摸球试验中,摸到白球的频数为40,可知摸到白球的频率为0.1.当试验次数很大时,用频率作为概率的估计值,可以估计摸到白球的概率约为0.1.
设袋中有红球x个,则袋中共有球(x+5)个,从袋中任意摸出1个球是白球的概率为P(摸到白球)= .
这样,我们可以估计袋中约有红球45个.
,得x=45.
鱼塘内养了若干条青鱼,怎样估计鱼塘内青鱼的条数呢?这个问题与“数学实验室”中的摸球游戏有怎样的联系?
把鱼塘内的青鱼看成“红球”.
往鱼塘内投放若干条白鱼,把白鱼看成“白球”.
对于这个问题,我们可以先往鱼塘内投放若干条白鱼,然后进行多次捕捞(每次捕捞后都放回,稍后再次捕捞),记录捕到的青鱼、白鱼的频数,计算捕到白鱼的频率并把它作为捕到白鱼的概率的估计值,就可以估算出鱼塘内青鱼的条数.例如:
设鱼塘内有青鱼N条,往鱼塘内投放自鱼60条,由多次捕捞、记数(每次捕捞后都放回,稍后再次捕捞),算得捕到白鱼的频率若为
并把它作为捕到白鱼的概率的估计值,则由P(捕到白鱼).
24
1
N+60
60
24
1
得N = 1380.这样,我们可以估计该鱼塘内约有青鱼1380条
我们也可以先从鱼塘内捕捞一些青鱼(如60条),并给每条青鱼做上记号(把这些青鱼看成“白鱼”),用上面的方法同样可以估计出该鱼塘内青鱼的条数.
在科学研究中,生物学家常常用上述方法估计某个种群的数量.例如,某地区的野鹿的只数,某山区某种鸟的数量,等等.
即在同样条件下,大量重复试验所得到的随机事件发生的频率的稳定值来估计这个事件发生的概率.
一个口袋中放有20个球,其中红球6个,白球和黑球若干个,每个球除了颜色外无任何区别.
(1)小王通过大量反复实验(每次取一个球,放回搅匀后再取)发现,取出黑球的概率稳定在1/4左右,请你估计袋中黑球的个数.
(2)若小王取出的第一个是白球,将它放在桌上,从袋中余下的球中在再任意取一个球,取出红球的概率是多少?
随堂练习
解:
(1)取出黑球的频率稳定在 左右,即可估计取出黑球的概率稳定为 ,袋中黑球的个数为 ×20=5个;
(2)由于白球的数目减少了1个,故总数减小为19,所以取出红球的概率增加了,变为
.
1.一只不透明的袋子中共装有360个红球、黄球和蓝球.小明每次从中任意摸出1个球,记下颜色后将球放回并搅匀,通过多次重复试验,算得摸到红球、黄球和蓝球的频率分别是25%,35%和40%,试估计这只袋子中3种颜色的球的数目.
2.质检部门对某批足球的质量进行检验,结果如下:
一般地,10000只该批足球中非优等品大约有多少只?
3.为估计鱼塘中鱼的数量,先从鱼塘中捕捞30条鱼做上标记,然后放回鱼塘.经过一段时间,待有标记的鱼完全混合于鱼群后,再从中多次捕捞,并算得平均每200条鱼中带有标记的鱼有5条.试估计该鱼塘中鱼的数量.
用频率去估计概率
用样本数据特征估计总体的数据特征
圆周率兀是无理数,它的值为3. 141 592 653 589 793 238 462 643 383……,圆周率兀在数学和其他学科中有着重要作用,从古到今世界各国数学家都曾孜孜不倦地寻求过兀值的计算方法.下面我们通过试验,应用统计与概率知识来估计它的值.
一个口袋中放有20个球,其中红球6个,白球和黑球个若干个,每个球出了颜色外没有任何区别.
(1)小王通过大量反复实验(每次取一个球,放回搅匀后再取)发现,取出黑球的概率稳定在1/4左右,请你估计袋中黑球的个数.
(2)若小王取出的第一个是白球,将它放在桌上,从袋中余下的球中在再任意取一个球,取出红球的概率是多少?
练一练
生物学家估计某一地区的野鹿只数时,常采用“捉放捉”的方法即先捕捉野鹿n只,分别给它们做上记号,然后放归:一段时间后,重新捕捉一些野鹿作为样本.像这样有放回地捕捉多次,如果平均每m只野鹿中带有记号的野鹿有a只,试估计该地区野鹿的只数(用含m,n,a的代数式表示).
频数:
在考察中,每个对象出现的次数称为频数.
频率:
而每个对象出现的次数与总次数的比值称为频率.
概率:
知识回顾
在数学中,我们把事件发生的可能性的大小称为事件发生的概率.
如果事件发生的各种可能结果的可能性相同,
事件A发生的可能的结果总数为m.
结果总数为n.
知识回顾
一只不透明的袋子中装有若干个白球和红球,这些球除颜色外都相同.做摸球实验:
(1)两人一组,一人从袋中任意摸出1个球,另一个人记下颜色后将球放回并搅匀,各组连续做20次这样的实验;
(2)汇总全班各组数据,并填表:
数学实验室:
你能根据试验的结果估计袋子中白球数与红球数的比吗?
8.5 概率帮你做估计
探索活动:
假设全班一共做了400次这样的摸球试验,摸到白球的频数为40,已知袋中有白球5个,你能估计袋中红球的个数吗?
8.5 概率帮你做估计
情境创设:
抛一枚硬币,正面朝上的概率是?
观察下面的试验数据:
8.5 概率帮你做估计
为了估计湖里有多少条鱼,先从湖里捕捞100条鱼做上标记,然后再放回湖里去,经过一段时间,待有标记的鱼完全混合于鱼群后,第二次再捕捞200条鱼,若其中25条有标记,那么请你估计湖里大约有多少条鱼?
情境创设:
8.5 概率帮你做估计
在研究工作中,生态学家经常要确定生物种群的数量,由于生物种群可能数量很多,或者分布很广,很难找到所用的生物个体.这时,他们往往利用“生物取样”的方法来估计种群的数量.
生物取样:就是在一个小区域内统计生物种群的数量(一个样本),假设这个样本与较大区域是相同的生物种群密度,统计这个小区域内的生物种群的数量,然后再乘以相应的倍数,即可确定一个较大区域的生物种群的数量.
8.5 概率帮你做估计
某车间生产的零件不合格的概率为 .
从他们生产的零件中每天任取10个做实验,平均来说,多少天会查到一个次品?
分析:先求出每天抽出次品的概率,然后可求出查到一个次品所需天数.
100天.
8.5 概率帮你做估计
随堂练习
1.一只不透明的袋子中共装有360个红球、黄球和蓝球.小明每次从中任意摸出1个球,记下颜色后将球放回并搅匀,通过多次重复试验,算得摸到红球、黄球和蓝球的频率分别是25%,35%和40%,试估计这只袋子中3种颜色的球的数目.
8.5 概率帮你做估计
练习
8.5 概率帮你做估计
练习
2.为估计鱼塘中鱼的数量,先从鱼塘中捕捞30条鱼做上标记,然后放回鱼塘.经过一段时间,待有标记的鱼完全混合于鱼群后,再从中多次捕捞,并算得平均每200条鱼中带有标记的鱼有5条.试估计该鱼塘中鱼的数量.
3.某射击运动员在同一条件下练习射击,结果如下表所示:
射击次数n
10
20
50
100
200
500
击中靶心次数m
8
19
44
92
178
452
击中靶心频率m/n
计算表中击中靶心的各个频率并填入表中.
8.5 概率帮你做估计
练习
4.质检部门对某批足球的质量进行检验,结果如下:
一般地,10000只该批足球中非优等品大约有多少只?
解:优等品频率大约是:
(0.92+0.93+0.97+0.944+0.953+0.951)÷6≈0.945
∴非优等品频率大约是:1-0.945=0.055
∴10000只该批足球中非优等品大约有:
10000×0.055=550(只)
5.为估计鱼塘中鱼的数量,先从鱼塘中捕捞30条鱼做上标记,然后放回鱼塘.经过一段时间,待有标记的鱼完全混合于鱼群后,再从中多次捕捞,并算得平均每200条鱼中带有标记的鱼有5条.试估计该鱼塘中鱼的数量.
解:设该鱼塘中鱼的数量为x条.
则 P=
得: x=1200
∴该鱼塘中鱼的数量大约为1200条.
频数:每个对象出现的次数称为频数.
频率:而每个对象出现的次数与总次数的比值称为频率.思考:频率与概率之间的关系?
小结:大量重复试验所得到的随机事件发生的实际频率接近于该事件发生的理论概率.
8.5 概率帮你做估计
小结:
谢谢聆听
2020-2021学年度苏科版九年级下册
第8章 统计和概率的简单应用
频数:
在考察中,每个对象出现的次数称为频数
频率:
而每个对象出现的次数与总次数的比值称为频率.
概率:
概念回顾
P(A)=
m
n
在数学中,我们把事件发生的可能性的大小
称为事件发生的概率
如果事件发生的每种可能结果的可能性相同,
事件A发生的可能的结果总数为m
结果总数为n
概念回顾
一只不透明的袋子中装有若干个白球和红球,这些球除颜色外都相同.做下列摸球试验:
(1)两人一组,将全班学生分成若干组;
(2)每次从中任意摸出1个球,记下颜色后将球放回并搅匀,各小组连续做20次这样的试验;
(3)汇总各组数据,并填表:
根据试验的结果,你能估计袋子中白球数与红球数的比吗?
假设全班一共做了400次这样的摸球试验,摸到白球的频数为40且已知袋中有白球5个,你能估计袋中红球的个数吗?
由400次摸球试验中,摸到白球的频数为40,可知摸到白球的频率为0.1.当试验次数很大时,用频率作为概率的估计值,可以估计摸到白球的概率约为0.1.
设袋中有红球x个,则袋中共有球(x+5)个,从袋中任意摸出1个球是白球的概率为P(摸到白球)= .
这样,我们可以估计袋中约有红球45个.
,得x=45.
鱼塘内养了若干条青鱼,怎样估计鱼塘内青鱼的条数呢?这个问题与“数学实验室”中的摸球游戏有怎样的联系?
把鱼塘内的青鱼看成“红球”.
往鱼塘内投放若干条白鱼,把白鱼看成“白球”.
对于这个问题,我们可以先往鱼塘内投放若干条白鱼,然后进行多次捕捞(每次捕捞后都放回,稍后再次捕捞),记录捕到的青鱼、白鱼的频数,计算捕到白鱼的频率并把它作为捕到白鱼的概率的估计值,就可以估算出鱼塘内青鱼的条数.例如:
设鱼塘内有青鱼N条,往鱼塘内投放自鱼60条,由多次捕捞、记数(每次捕捞后都放回,稍后再次捕捞),算得捕到白鱼的频率若为
并把它作为捕到白鱼的概率的估计值,则由P(捕到白鱼).
24
1
N+60
60
24
1
得N = 1380.这样,我们可以估计该鱼塘内约有青鱼1380条
我们也可以先从鱼塘内捕捞一些青鱼(如60条),并给每条青鱼做上记号(把这些青鱼看成“白鱼”),用上面的方法同样可以估计出该鱼塘内青鱼的条数.
在科学研究中,生物学家常常用上述方法估计某个种群的数量.例如,某地区的野鹿的只数,某山区某种鸟的数量,等等.
即在同样条件下,大量重复试验所得到的随机事件发生的频率的稳定值来估计这个事件发生的概率.
一个口袋中放有20个球,其中红球6个,白球和黑球若干个,每个球除了颜色外无任何区别.
(1)小王通过大量反复实验(每次取一个球,放回搅匀后再取)发现,取出黑球的概率稳定在1/4左右,请你估计袋中黑球的个数.
(2)若小王取出的第一个是白球,将它放在桌上,从袋中余下的球中在再任意取一个球,取出红球的概率是多少?
随堂练习
解:
(1)取出黑球的频率稳定在 左右,即可估计取出黑球的概率稳定为 ,袋中黑球的个数为 ×20=5个;
(2)由于白球的数目减少了1个,故总数减小为19,所以取出红球的概率增加了,变为
.
1.一只不透明的袋子中共装有360个红球、黄球和蓝球.小明每次从中任意摸出1个球,记下颜色后将球放回并搅匀,通过多次重复试验,算得摸到红球、黄球和蓝球的频率分别是25%,35%和40%,试估计这只袋子中3种颜色的球的数目.
2.质检部门对某批足球的质量进行检验,结果如下:
一般地,10000只该批足球中非优等品大约有多少只?
3.为估计鱼塘中鱼的数量,先从鱼塘中捕捞30条鱼做上标记,然后放回鱼塘.经过一段时间,待有标记的鱼完全混合于鱼群后,再从中多次捕捞,并算得平均每200条鱼中带有标记的鱼有5条.试估计该鱼塘中鱼的数量.
用频率去估计概率
用样本数据特征估计总体的数据特征
圆周率兀是无理数,它的值为3. 141 592 653 589 793 238 462 643 383……,圆周率兀在数学和其他学科中有着重要作用,从古到今世界各国数学家都曾孜孜不倦地寻求过兀值的计算方法.下面我们通过试验,应用统计与概率知识来估计它的值.
一个口袋中放有20个球,其中红球6个,白球和黑球个若干个,每个球出了颜色外没有任何区别.
(1)小王通过大量反复实验(每次取一个球,放回搅匀后再取)发现,取出黑球的概率稳定在1/4左右,请你估计袋中黑球的个数.
(2)若小王取出的第一个是白球,将它放在桌上,从袋中余下的球中在再任意取一个球,取出红球的概率是多少?
练一练
生物学家估计某一地区的野鹿只数时,常采用“捉放捉”的方法即先捕捉野鹿n只,分别给它们做上记号,然后放归:一段时间后,重新捕捉一些野鹿作为样本.像这样有放回地捕捉多次,如果平均每m只野鹿中带有记号的野鹿有a只,试估计该地区野鹿的只数(用含m,n,a的代数式表示).
频数:
在考察中,每个对象出现的次数称为频数.
频率:
而每个对象出现的次数与总次数的比值称为频率.
概率:
知识回顾
在数学中,我们把事件发生的可能性的大小称为事件发生的概率.
如果事件发生的各种可能结果的可能性相同,
事件A发生的可能的结果总数为m.
结果总数为n.
知识回顾
一只不透明的袋子中装有若干个白球和红球,这些球除颜色外都相同.做摸球实验:
(1)两人一组,一人从袋中任意摸出1个球,另一个人记下颜色后将球放回并搅匀,各组连续做20次这样的实验;
(2)汇总全班各组数据,并填表:
数学实验室:
你能根据试验的结果估计袋子中白球数与红球数的比吗?
8.5 概率帮你做估计
探索活动:
假设全班一共做了400次这样的摸球试验,摸到白球的频数为40,已知袋中有白球5个,你能估计袋中红球的个数吗?
8.5 概率帮你做估计
情境创设:
抛一枚硬币,正面朝上的概率是?
观察下面的试验数据:
8.5 概率帮你做估计
为了估计湖里有多少条鱼,先从湖里捕捞100条鱼做上标记,然后再放回湖里去,经过一段时间,待有标记的鱼完全混合于鱼群后,第二次再捕捞200条鱼,若其中25条有标记,那么请你估计湖里大约有多少条鱼?
情境创设:
8.5 概率帮你做估计
在研究工作中,生态学家经常要确定生物种群的数量,由于生物种群可能数量很多,或者分布很广,很难找到所用的生物个体.这时,他们往往利用“生物取样”的方法来估计种群的数量.
生物取样:就是在一个小区域内统计生物种群的数量(一个样本),假设这个样本与较大区域是相同的生物种群密度,统计这个小区域内的生物种群的数量,然后再乘以相应的倍数,即可确定一个较大区域的生物种群的数量.
8.5 概率帮你做估计
某车间生产的零件不合格的概率为 .
从他们生产的零件中每天任取10个做实验,平均来说,多少天会查到一个次品?
分析:先求出每天抽出次品的概率,然后可求出查到一个次品所需天数.
100天.
8.5 概率帮你做估计
随堂练习
1.一只不透明的袋子中共装有360个红球、黄球和蓝球.小明每次从中任意摸出1个球,记下颜色后将球放回并搅匀,通过多次重复试验,算得摸到红球、黄球和蓝球的频率分别是25%,35%和40%,试估计这只袋子中3种颜色的球的数目.
8.5 概率帮你做估计
练习
8.5 概率帮你做估计
练习
2.为估计鱼塘中鱼的数量,先从鱼塘中捕捞30条鱼做上标记,然后放回鱼塘.经过一段时间,待有标记的鱼完全混合于鱼群后,再从中多次捕捞,并算得平均每200条鱼中带有标记的鱼有5条.试估计该鱼塘中鱼的数量.
3.某射击运动员在同一条件下练习射击,结果如下表所示:
射击次数n
10
20
50
100
200
500
击中靶心次数m
8
19
44
92
178
452
击中靶心频率m/n
计算表中击中靶心的各个频率并填入表中.
8.5 概率帮你做估计
练习
4.质检部门对某批足球的质量进行检验,结果如下:
一般地,10000只该批足球中非优等品大约有多少只?
解:优等品频率大约是:
(0.92+0.93+0.97+0.944+0.953+0.951)÷6≈0.945
∴非优等品频率大约是:1-0.945=0.055
∴10000只该批足球中非优等品大约有:
10000×0.055=550(只)
5.为估计鱼塘中鱼的数量,先从鱼塘中捕捞30条鱼做上标记,然后放回鱼塘.经过一段时间,待有标记的鱼完全混合于鱼群后,再从中多次捕捞,并算得平均每200条鱼中带有标记的鱼有5条.试估计该鱼塘中鱼的数量.
解:设该鱼塘中鱼的数量为x条.
则 P=
得: x=1200
∴该鱼塘中鱼的数量大约为1200条.
频数:每个对象出现的次数称为频数.
频率:而每个对象出现的次数与总次数的比值称为频率.思考:频率与概率之间的关系?
小结:大量重复试验所得到的随机事件发生的实际频率接近于该事件发生的理论概率.
8.5 概率帮你做估计
小结:
谢谢聆听
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
