16.1.2 二次根式的性质 课件(共18张PPT)
文档属性
| 名称 | 16.1.2 二次根式的性质 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 18:39:36 | ||
图片预览





文档简介
(共18张PPT)
16.1 二次根式
第十六章 二次根式
2021年春人教版八年级(下)数学
(第二课时 二次根式的性质)
学习目标
1.根据算术平方根的意义了解二次根式的概念,知道被开方数
必须是非负数的理由;
2.理解二次根式的性质,会利用二次根式的性质解决简单问题;
3.了解代数式的概念,初步体会代数式在表示数量关系上的作用.
探索与思考
求下列各数的算术平方根:
0
根据算术平方根的意义填空:
=
=
=
=
=2
=
=0
观察两边式子的结构,你发现了什么?
二次根式的性质
计算:
1)
2)
= × (=4×6=24
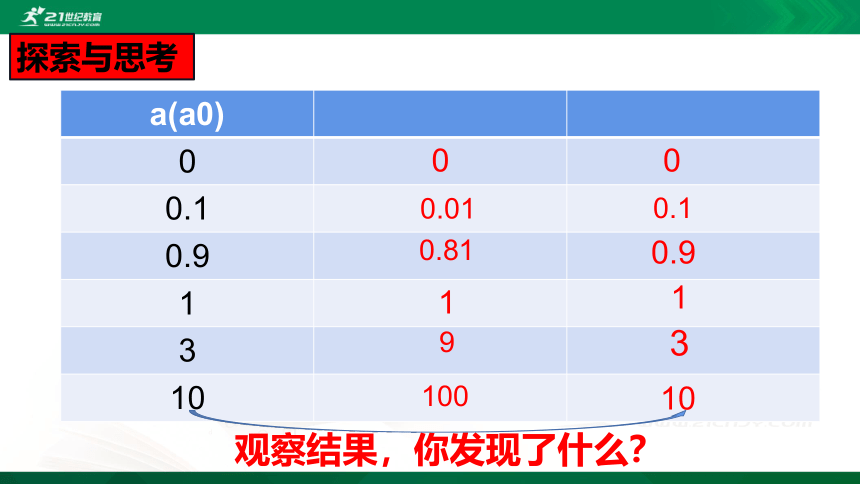
a(a0)
0
0.1
0.9
1
3
10
0
0
0.01
0.1
0.81
0.9
1
1
9
3
100
10
观察结果,你发现了什么?
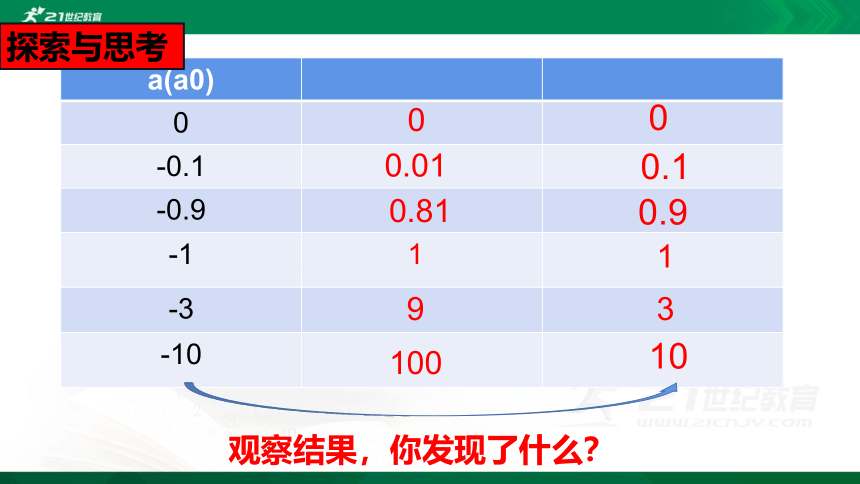
探索与思考
a(a0)
0
-0.1
-0.9
-1
-3
-10
0
0
0.01
0.1
0.81
0.9
1
1
9
3
100
10
观察结果,你发现了什么?
探索与思考
2
0.2
0
计算:
1)
2)
3)
4)
二次根式的性质二
a(a≥0)
-a(a<0)
即任意一个数的平方的算术平方根
等于它本身的绝对值 .
探索与思考
计算:
1)
2)
3)
=3
=5
=π-3.14
针对练习
从运算顺序看
从取值范围看
从运算结果看
意义
先开方 , 后平方
先平方 , 后开方
a≥0
a取任何实数
a
|a|
表示一个非负数a
的算术平方根的平方
表示一个实数 a
的平方的算术平方根
探索与思考
1.若=2﹣a,则a的取值范围是( )
A.a=2 B.a>2 C.a≥2 D.a≤2
【答案】D
【解析】
∵=2-ɑ,∴a-2≤0,即a≤2,故选D.
2. 化简(﹣)2的结果是( )
A.±5 B.﹣5 C.5 D.5
课堂练习
D
3. 计算:
1)
2)
【答案】(1);(2)6.
【详解】
(1)原式==
(2)原式=3+4+1-2=6.
3.已知x<1,则化简的结果是( )
A.x-1 B.1-x C.-x-1 D.1+x
【答案】B
【详解】
∵x<1,∴x-1<0,
∴=|x-1|=1-x.
故选B.
4.实数a,b在数轴上对应点的位置如图所示,化简的结果是( )
A. B. C. D.
a
0
b
【答案】A
【详解】
由图可知:a<0,a b<0,
则
= a (a b)
= 2a+b.
故选:A.
5.如图,a,b,c在数轴上的位置如图所示,化简的结果是( )
A.2c﹣b B.﹣b C.b D.﹣2a﹣b
【答案】A
【详解】
根据数轴可以得到:a<b<0<c,且|a|>|c|,则a+c<0,c﹣b>0,
则原式=﹣a+(a+c)+(c﹣b)=﹣a+a+c+c﹣b=2c﹣b.
故选A.
6.实数a、b在数轴上的位置如图所示,请化简:|a|﹣﹣
【答案】-b
【解析】
∵从数轴可知:a<0<b,
∴|a|﹣﹣
=|a|﹣|a|﹣|b|
=﹣|b|
=﹣b.
a≥0
≥0
回顾本课的学习,回答以下问题:
二次根式具有哪些性质?
二次根式 的双重非负性
两个重要关系式
课堂小结
谢谢聆听
16.1 二次根式
第十六章 二次根式
2021年春人教版八年级(下)数学
(第二课时 二次根式的性质)
学习目标
1.根据算术平方根的意义了解二次根式的概念,知道被开方数
必须是非负数的理由;
2.理解二次根式的性质,会利用二次根式的性质解决简单问题;
3.了解代数式的概念,初步体会代数式在表示数量关系上的作用.
探索与思考
求下列各数的算术平方根:
0
根据算术平方根的意义填空:
=
=
=
=
=2
=
=0
观察两边式子的结构,你发现了什么?
二次根式的性质
计算:
1)
2)
= × (=4×6=24
a(a0)
0
0.1
0.9
1
3
10
0
0
0.01
0.1
0.81
0.9
1
1
9
3
100
10
观察结果,你发现了什么?
探索与思考
a(a0)
0
-0.1
-0.9
-1
-3
-10
0
0
0.01
0.1
0.81
0.9
1
1
9
3
100
10
观察结果,你发现了什么?
探索与思考
2
0.2
0
计算:
1)
2)
3)
4)
二次根式的性质二
a(a≥0)
-a(a<0)
即任意一个数的平方的算术平方根
等于它本身的绝对值 .
探索与思考
计算:
1)
2)
3)
=3
=5
=π-3.14
针对练习
从运算顺序看
从取值范围看
从运算结果看
意义
先开方 , 后平方
先平方 , 后开方
a≥0
a取任何实数
a
|a|
表示一个非负数a
的算术平方根的平方
表示一个实数 a
的平方的算术平方根
探索与思考
1.若=2﹣a,则a的取值范围是( )
A.a=2 B.a>2 C.a≥2 D.a≤2
【答案】D
【解析】
∵=2-ɑ,∴a-2≤0,即a≤2,故选D.
2. 化简(﹣)2的结果是( )
A.±5 B.﹣5 C.5 D.5
课堂练习
D
3. 计算:
1)
2)
【答案】(1);(2)6.
【详解】
(1)原式==
(2)原式=3+4+1-2=6.
3.已知x<1,则化简的结果是( )
A.x-1 B.1-x C.-x-1 D.1+x
【答案】B
【详解】
∵x<1,∴x-1<0,
∴=|x-1|=1-x.
故选B.
4.实数a,b在数轴上对应点的位置如图所示,化简的结果是( )
A. B. C. D.
a
0
b
【答案】A
【详解】
由图可知:a<0,a b<0,
则
= a (a b)
= 2a+b.
故选:A.
5.如图,a,b,c在数轴上的位置如图所示,化简的结果是( )
A.2c﹣b B.﹣b C.b D.﹣2a﹣b
【答案】A
【详解】
根据数轴可以得到:a<b<0<c,且|a|>|c|,则a+c<0,c﹣b>0,
则原式=﹣a+(a+c)+(c﹣b)=﹣a+a+c+c﹣b=2c﹣b.
故选A.
6.实数a、b在数轴上的位置如图所示,请化简:|a|﹣﹣
【答案】-b
【解析】
∵从数轴可知:a<0<b,
∴|a|﹣﹣
=|a|﹣|a|﹣|b|
=﹣|b|
=﹣b.
a≥0
≥0
回顾本课的学习,回答以下问题:
二次根式具有哪些性质?
二次根式 的双重非负性
两个重要关系式
课堂小结
谢谢聆听
