2020--2021学年八年级数学人教版下册第18章《平行四边形》常考题专练(三)(word版,含答案)
文档属性
| 名称 | 2020--2021学年八年级数学人教版下册第18章《平行四边形》常考题专练(三)(word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 134.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 00:00:00 | ||
图片预览


文档简介
2020--2021学年八年级下册第18章《平行四边形》
常考题专练(三)
1.如图,在?ABCD中,
(1)若点E、F是AD、BC的中点,连接BE、DF,求证:BE=DF.
(2)若BE平分∠ABC且交边AD于点E,如果AB=6cm,BC=10cm,试求线段DE的长.
2.如图,在△ABC中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE,连结BF,CE.
(1)求证:四边形BFCE是平行四边形;
(2)当边AB、AC满足什么条件时,四边形BECF是菱形?并说明理由.
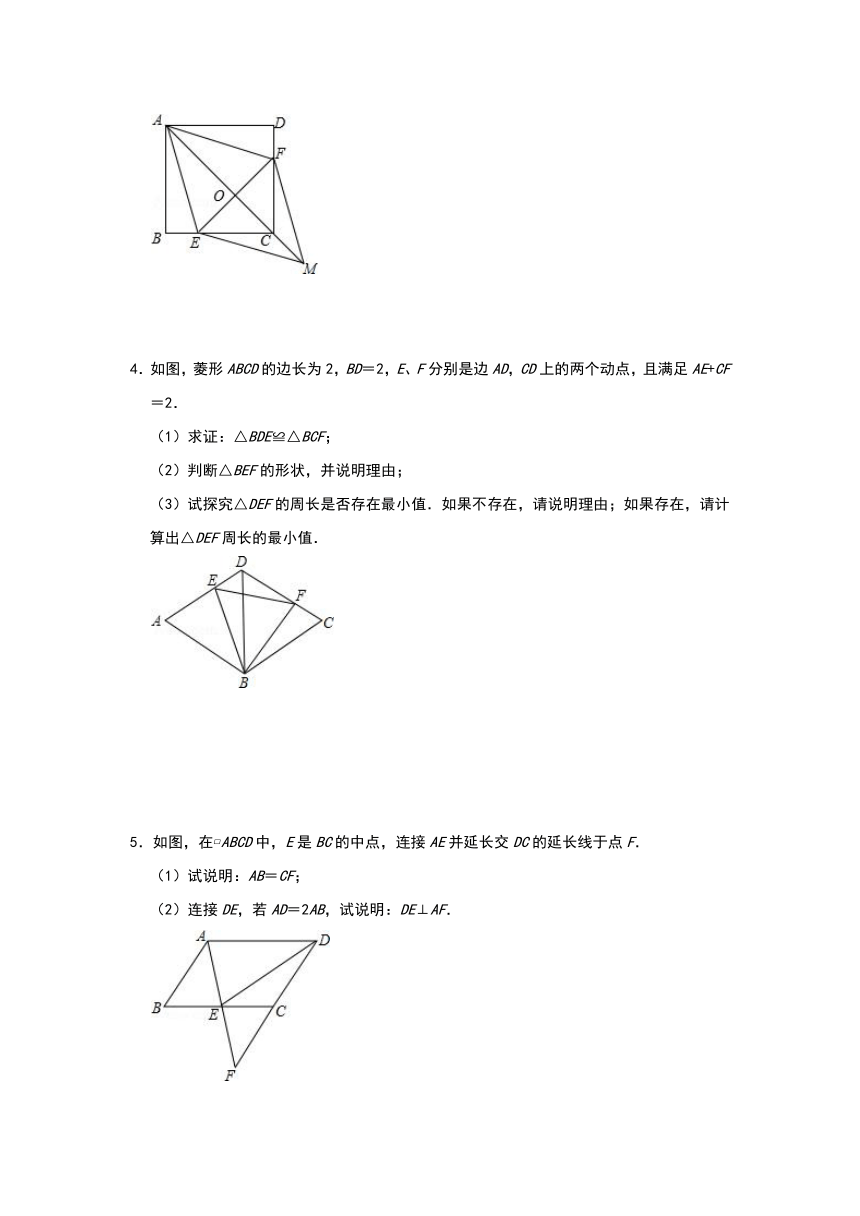
3.如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
(1)求证:CE=CF.
(2)连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
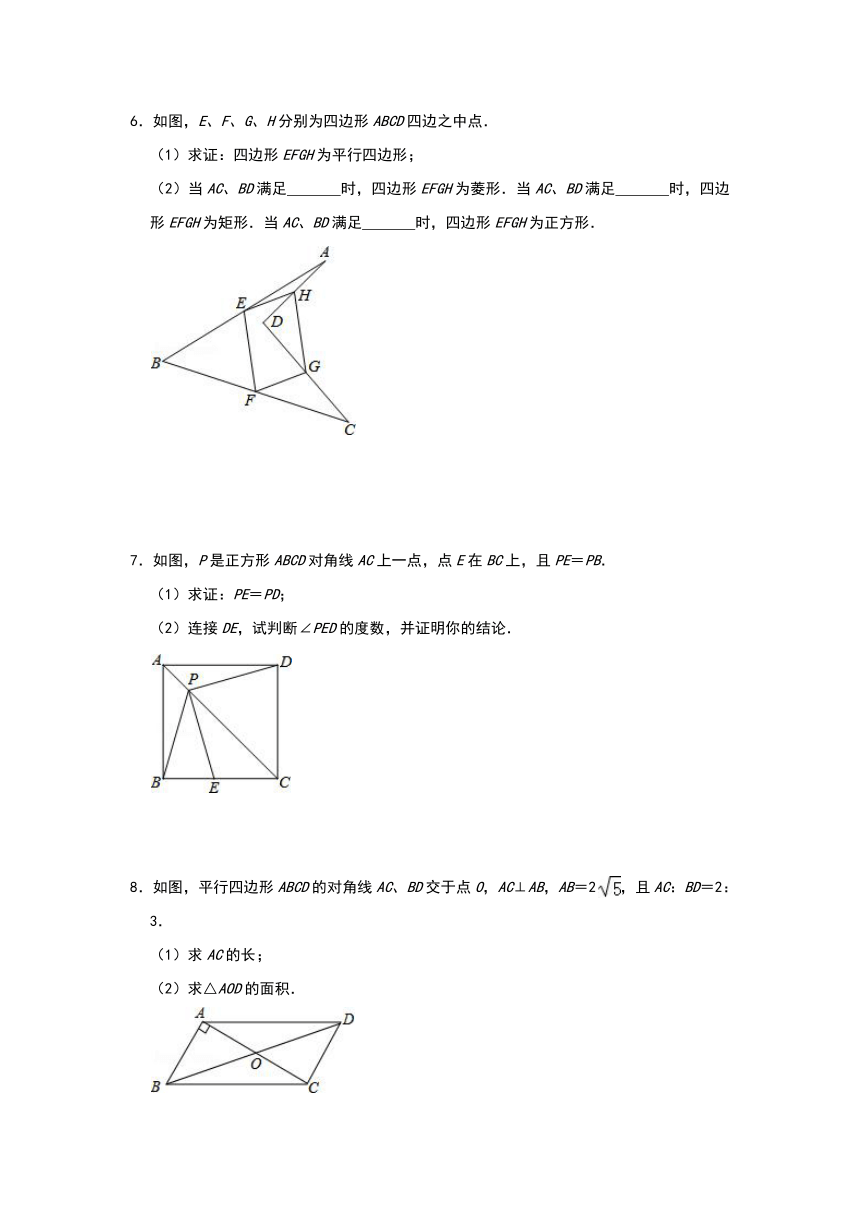
4.如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2.
(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由;
(3)试探究△DEF的周长是否存在最小值.如果不存在,请说明理由;如果存在,请计算出△DEF周长的最小值.
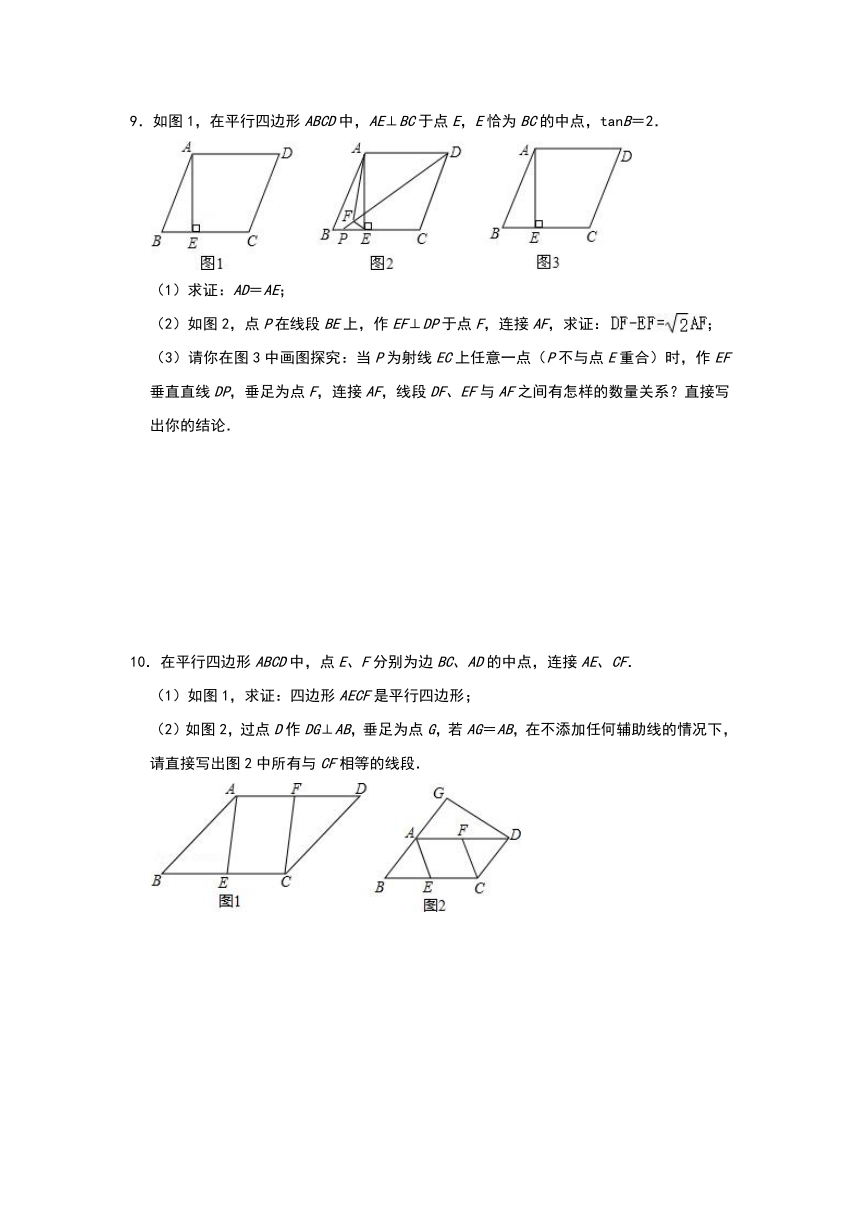
5.如图,在?ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.
(1)试说明:AB=CF;
(2)连接DE,若AD=2AB,试说明:DE⊥AF.
6.如图,E、F、G、H分别为四边形ABCD四边之中点.
(1)求证:四边形EFGH为平行四边形;
(2)当AC、BD满足
时,四边形EFGH为菱形.当AC、BD满足
时,四边形EFGH为矩形.当AC、BD满足
时,四边形EFGH为正方形.
7.如图,P是正方形ABCD对角线AC上一点,点E在BC上,且PE=PB.
(1)求证:PE=PD;
(2)连接DE,试判断∠PED的度数,并证明你的结论.
8.如图,平行四边形ABCD的对角线AC、BD交于点O,AC⊥AB,AB=2,且AC:BD=2:3.
(1)求AC的长;
(2)求△AOD的面积.
9.如图1,在平行四边形ABCD中,AE⊥BC于点E,E恰为BC的中点,tanB=2.
(1)求证:AD=AE;
(2)如图2,点P在线段BE上,作EF⊥DP于点F,连接AF,求证:;
(3)请你在图3中画图探究:当P为射线EC上任意一点(P不与点E重合)时,作EF垂直直线DP,垂足为点F,连接AF,线段DF、EF与AF之间有怎样的数量关系?直接写出你的结论.
10.在平行四边形ABCD中,点E、F分别为边BC、AD的中点,连接AE、CF.
(1)如图1,求证:四边形AECF是平行四边形;
(2)如图2,过点D作DG⊥AB,垂足为点G,若AG=AB,在不添加任何辅助线的情况下,请直接写出图2中所有与CF相等的线段.
参考答案
1.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵点E、F分别是?ABCD边AD、BC的中点,
∴DE=AD,BF=BC,
∴DE=BF,
∴四边形BFDE是平行四边形,
∴BE=DF.
(2)解:∵AD∥BC,
∴∠AEB=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AE=AB=6cm,
∴DE=AD﹣AE=10cm﹣6cm=4cm.
2.(1)证明:∵在△ABC中,D是BC边的中点,
∴BD=CD,
∵CF∥BE,
∴∠CFD=∠BED,
在△CFD和△BED中,
,
∴△CFD≌△BED(AAS),
∴CF=BE,
∴四边形BFCE是平行四边形;
(2)解:当AB=AC时,四边形BECF是菱形;理由如下:
∵AB=AC,D是BC边的中点,
∴AD⊥BC,
∴EF⊥BC,
∴四边形BECF是菱形.
3.(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠B=∠D=90°,
在Rt△ABE和Rt△ADF中,
,
∴Rt△ADF≌Rt△ABE(HL)
∴BE=DF,
∵BC=DC,
∴CE=CF;
(2)解:四边形AEMF是菱形,理由为:
∵四边形ABCD是正方形,
∴∠BCA=∠DCA=45°,
在△COE和△COF中,
,
∴△COE≌△COF(SAS),
∴OE=OF,又OM=OA,
∴四边形AEMF是平行四边形,
∵AE=AF,
∴平行四边形AEMF是菱形.
4.(1)证明:∵菱形ABCD的边长为2,对角线BD=2,
∴AB=AD=BD=2,BC=CD=BD=2,
∴△ABD与△BCD都是等边三角形,
∴∠BDE=∠C=60°,
∵AE+CF=2,
∴CF=2﹣AE,
又∵DE=AD﹣AE=2﹣AE,
∴DE=CF,
在△BDE和△BCF中,
,
∴△BDE≌△BCF(SAS);
(2)解:△BEF是等边三角形.理由如下:
由(1)可知△BDE≌△BCF,
∴BE=BF,∠DBE=∠CBF,
∴∠EBF=∠DBE+∠DBF=∠CBF+∠DBF=∠DBC=60°,
∴△BEF是等边三角形,
由图可知,△BDE绕点B顺时针旋转60°即可得到△BCF;
(3)解:如图所示:
当BE⊥AD时,△DEF的周长最小,
∵△BDE≌△BCF,
∴DE=FC,
∴DE+DF=AD=2,
故当△DEF的周长最小,则EF最小即可,
∵△BEF是等边三角形,△ABD与△BCD都是等边三角形,
∴BE=ABsin60°=,
∴△DEF周长的最小值为:2+.
5.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥DF,
∴∠ABE=∠FCE,
∵E为BC中点,
∴BE=CE,
在△ABE与△FCE中,
,
∴△ABE≌△FCE(ASA),
∴AB=FC;
(2)∵AD=2AB,AB=FC=CD,
∴AD=DF,
∵△ABE≌△FCE,
∴AE=EF,
∴DE⊥AF.
6.(1)证明:如图,连接BD,
∵E、F、G、H分别为四边形ABCD四边之中点,
∴EH是△ABD的中位线,FG是△BCD的中位线,
∴EH∥BD且EH=BD,FG∥BD且FG=BD,
∴EH∥FG且EH=FG,
∴四边形EFGH为平行四边形;
(2)解:连接AC,
同理可得EF∥AC且EF=AC,
所以,AC=BD时,四边形EFGH为菱形;
AC⊥BD时,四边形EFGH为矩形;
AC=BD且AC⊥BD时,四边形EFGH为正方形.
故答案为:AC=BD;AC⊥BD;AC=BD且AC⊥BD.
7.(1)证明:∵四边形ABCD是正方形,
∴BC=CD,∠ACB=∠ACD,
在△PBC和△PDC中,
,
∴△PBC≌△PDC(SAS),
∴PB=PD,
∵PE=PB,
∴PE=PD;
(2)判断∠PED=45°.
证明:∵四边形ABCD是正方形,
∴∠BCD=90°,
∵△PBC≌△PDC,
∴∠PBC=∠PDC,
∵PE=PB,
∴∠PBC=∠PEB,
∴∠PDC=∠PEB,
∵∠PEB+∠PEC=180°,
∴∠PDC+∠PEC=180°,
在四边形PECD中,∠EPD=360°﹣(∠PDC+∠PEC)﹣∠BCD=360°﹣180°﹣90°=90°,
又∵PE=PD,
∴△PDE是等腰直角三角形,
∴∠PED=45°.
8.解:(1)∵四边形ABCD是平行四边形,
∴OA=AC,OB=BD,
∵AC:BD=2:3,
∴OA:OB=2:3,
设OA=2x,OB=3x,
∵AC⊥AB,AB=2,
∴(2x)2+(2)2=(3x)2,
解得:x=2,
∴OA=4,
∴AC=8;
(2)∵S△ABD=S△ABC=AB?AC=×2×8=8,
∴S△AOD=S△ABD=×8=4.
9.(1)证明:∵tanB=2,
∴AE=2BE;
∵E是BC中点,
∴BC=2BE,
即AE=BC;
又∵四边形ABCD是平行四边形,则AD=BC=AE;
(2)证明:作AG⊥AF,交DP于G;(如图2)
∵AD∥BC,
∴∠ADG=∠DPC;
∵∠AEP=∠EFP=90°,
∴∠PEF+∠EPF=∠PEF+∠AEF=90°,
即∠ADG=∠AEF=∠FPE;
又∵AE=AD,∠FAE=∠GAD=90°﹣∠EAG,
∴△AFE≌△AGD,
∴AF=AG,即△AFG是等腰直角三角形,且EF=DG;
∴FG=AF,且DF=DG+GF=EF+FG,
故DF﹣EF=AF;
(3)解:如图3,
①当EP在线段BC上时,有DF+EF=AF
②当EP≤2BC时,DF﹣EF=AF,解法同(2).
③当EP>2BC时,EF﹣DF=AF.
10.(1)证明:如图1中,∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵AF=AD,EC=BC,
∴AF=EC.AF∥EC,
∴四边形AECF是平行四边形.
(2)与CF相等的线段有:AF,DF,AE,BE.EC.
理由:如图2中,连接AC.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵AB=AG,
∴AG=CD,AG∥CD,
∴四边形ACDG是平行四边形,
∵∠G=90°,
∴四边形ACDG是矩形,
∴∠ACD=90°,∵AF=DF,
∴AF=CF=DF,
∵四边形AECF是平行四边形,
∴四边形AECF是菱形,
∴CF=AF=DF=AE=EC=BE.
常考题专练(三)
1.如图,在?ABCD中,
(1)若点E、F是AD、BC的中点,连接BE、DF,求证:BE=DF.
(2)若BE平分∠ABC且交边AD于点E,如果AB=6cm,BC=10cm,试求线段DE的长.
2.如图,在△ABC中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE,连结BF,CE.
(1)求证:四边形BFCE是平行四边形;
(2)当边AB、AC满足什么条件时,四边形BECF是菱形?并说明理由.
3.如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
(1)求证:CE=CF.
(2)连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
4.如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2.
(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由;
(3)试探究△DEF的周长是否存在最小值.如果不存在,请说明理由;如果存在,请计算出△DEF周长的最小值.
5.如图,在?ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.
(1)试说明:AB=CF;
(2)连接DE,若AD=2AB,试说明:DE⊥AF.
6.如图,E、F、G、H分别为四边形ABCD四边之中点.
(1)求证:四边形EFGH为平行四边形;
(2)当AC、BD满足
时,四边形EFGH为菱形.当AC、BD满足
时,四边形EFGH为矩形.当AC、BD满足
时,四边形EFGH为正方形.
7.如图,P是正方形ABCD对角线AC上一点,点E在BC上,且PE=PB.
(1)求证:PE=PD;
(2)连接DE,试判断∠PED的度数,并证明你的结论.
8.如图,平行四边形ABCD的对角线AC、BD交于点O,AC⊥AB,AB=2,且AC:BD=2:3.
(1)求AC的长;
(2)求△AOD的面积.
9.如图1,在平行四边形ABCD中,AE⊥BC于点E,E恰为BC的中点,tanB=2.
(1)求证:AD=AE;
(2)如图2,点P在线段BE上,作EF⊥DP于点F,连接AF,求证:;
(3)请你在图3中画图探究:当P为射线EC上任意一点(P不与点E重合)时,作EF垂直直线DP,垂足为点F,连接AF,线段DF、EF与AF之间有怎样的数量关系?直接写出你的结论.
10.在平行四边形ABCD中,点E、F分别为边BC、AD的中点,连接AE、CF.
(1)如图1,求证:四边形AECF是平行四边形;
(2)如图2,过点D作DG⊥AB,垂足为点G,若AG=AB,在不添加任何辅助线的情况下,请直接写出图2中所有与CF相等的线段.
参考答案
1.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵点E、F分别是?ABCD边AD、BC的中点,
∴DE=AD,BF=BC,
∴DE=BF,
∴四边形BFDE是平行四边形,
∴BE=DF.
(2)解:∵AD∥BC,
∴∠AEB=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AE=AB=6cm,
∴DE=AD﹣AE=10cm﹣6cm=4cm.
2.(1)证明:∵在△ABC中,D是BC边的中点,
∴BD=CD,
∵CF∥BE,
∴∠CFD=∠BED,
在△CFD和△BED中,
,
∴△CFD≌△BED(AAS),
∴CF=BE,
∴四边形BFCE是平行四边形;
(2)解:当AB=AC时,四边形BECF是菱形;理由如下:
∵AB=AC,D是BC边的中点,
∴AD⊥BC,
∴EF⊥BC,
∴四边形BECF是菱形.
3.(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠B=∠D=90°,
在Rt△ABE和Rt△ADF中,
,
∴Rt△ADF≌Rt△ABE(HL)
∴BE=DF,
∵BC=DC,
∴CE=CF;
(2)解:四边形AEMF是菱形,理由为:
∵四边形ABCD是正方形,
∴∠BCA=∠DCA=45°,
在△COE和△COF中,
,
∴△COE≌△COF(SAS),
∴OE=OF,又OM=OA,
∴四边形AEMF是平行四边形,
∵AE=AF,
∴平行四边形AEMF是菱形.
4.(1)证明:∵菱形ABCD的边长为2,对角线BD=2,
∴AB=AD=BD=2,BC=CD=BD=2,
∴△ABD与△BCD都是等边三角形,
∴∠BDE=∠C=60°,
∵AE+CF=2,
∴CF=2﹣AE,
又∵DE=AD﹣AE=2﹣AE,
∴DE=CF,
在△BDE和△BCF中,
,
∴△BDE≌△BCF(SAS);
(2)解:△BEF是等边三角形.理由如下:
由(1)可知△BDE≌△BCF,
∴BE=BF,∠DBE=∠CBF,
∴∠EBF=∠DBE+∠DBF=∠CBF+∠DBF=∠DBC=60°,
∴△BEF是等边三角形,
由图可知,△BDE绕点B顺时针旋转60°即可得到△BCF;
(3)解:如图所示:
当BE⊥AD时,△DEF的周长最小,
∵△BDE≌△BCF,
∴DE=FC,
∴DE+DF=AD=2,
故当△DEF的周长最小,则EF最小即可,
∵△BEF是等边三角形,△ABD与△BCD都是等边三角形,
∴BE=ABsin60°=,
∴△DEF周长的最小值为:2+.
5.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥DF,
∴∠ABE=∠FCE,
∵E为BC中点,
∴BE=CE,
在△ABE与△FCE中,
,
∴△ABE≌△FCE(ASA),
∴AB=FC;
(2)∵AD=2AB,AB=FC=CD,
∴AD=DF,
∵△ABE≌△FCE,
∴AE=EF,
∴DE⊥AF.
6.(1)证明:如图,连接BD,
∵E、F、G、H分别为四边形ABCD四边之中点,
∴EH是△ABD的中位线,FG是△BCD的中位线,
∴EH∥BD且EH=BD,FG∥BD且FG=BD,
∴EH∥FG且EH=FG,
∴四边形EFGH为平行四边形;
(2)解:连接AC,
同理可得EF∥AC且EF=AC,
所以,AC=BD时,四边形EFGH为菱形;
AC⊥BD时,四边形EFGH为矩形;
AC=BD且AC⊥BD时,四边形EFGH为正方形.
故答案为:AC=BD;AC⊥BD;AC=BD且AC⊥BD.
7.(1)证明:∵四边形ABCD是正方形,
∴BC=CD,∠ACB=∠ACD,
在△PBC和△PDC中,
,
∴△PBC≌△PDC(SAS),
∴PB=PD,
∵PE=PB,
∴PE=PD;
(2)判断∠PED=45°.
证明:∵四边形ABCD是正方形,
∴∠BCD=90°,
∵△PBC≌△PDC,
∴∠PBC=∠PDC,
∵PE=PB,
∴∠PBC=∠PEB,
∴∠PDC=∠PEB,
∵∠PEB+∠PEC=180°,
∴∠PDC+∠PEC=180°,
在四边形PECD中,∠EPD=360°﹣(∠PDC+∠PEC)﹣∠BCD=360°﹣180°﹣90°=90°,
又∵PE=PD,
∴△PDE是等腰直角三角形,
∴∠PED=45°.
8.解:(1)∵四边形ABCD是平行四边形,
∴OA=AC,OB=BD,
∵AC:BD=2:3,
∴OA:OB=2:3,
设OA=2x,OB=3x,
∵AC⊥AB,AB=2,
∴(2x)2+(2)2=(3x)2,
解得:x=2,
∴OA=4,
∴AC=8;
(2)∵S△ABD=S△ABC=AB?AC=×2×8=8,
∴S△AOD=S△ABD=×8=4.
9.(1)证明:∵tanB=2,
∴AE=2BE;
∵E是BC中点,
∴BC=2BE,
即AE=BC;
又∵四边形ABCD是平行四边形,则AD=BC=AE;
(2)证明:作AG⊥AF,交DP于G;(如图2)
∵AD∥BC,
∴∠ADG=∠DPC;
∵∠AEP=∠EFP=90°,
∴∠PEF+∠EPF=∠PEF+∠AEF=90°,
即∠ADG=∠AEF=∠FPE;
又∵AE=AD,∠FAE=∠GAD=90°﹣∠EAG,
∴△AFE≌△AGD,
∴AF=AG,即△AFG是等腰直角三角形,且EF=DG;
∴FG=AF,且DF=DG+GF=EF+FG,
故DF﹣EF=AF;
(3)解:如图3,
①当EP在线段BC上时,有DF+EF=AF
②当EP≤2BC时,DF﹣EF=AF,解法同(2).
③当EP>2BC时,EF﹣DF=AF.
10.(1)证明:如图1中,∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵AF=AD,EC=BC,
∴AF=EC.AF∥EC,
∴四边形AECF是平行四边形.
(2)与CF相等的线段有:AF,DF,AE,BE.EC.
理由:如图2中,连接AC.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵AB=AG,
∴AG=CD,AG∥CD,
∴四边形ACDG是平行四边形,
∵∠G=90°,
∴四边形ACDG是矩形,
∴∠ACD=90°,∵AF=DF,
∴AF=CF=DF,
∵四边形AECF是平行四边形,
∴四边形AECF是菱形,
∴CF=AF=DF=AE=EC=BE.
