6.5 整式的乘法同步练习（含答案）

中小学教育资源及组卷应用平台
第六章 整式的乘除
5 整式的乘法
知识能力全练
知识点一 单项式与单项式相乘
1.计算2a2b3·（-3a）的结果是（ ）
A.-6a3b3 B.6a2b3 C.6a3b3 D.-6a2b3
2.-m2n2·（-m3n6）的计算结果是（ ）
A.m3n2 B.-m3n8 C.m5n8 D.-m5n8
3.计算:3x2·2x2y＝___________.
4.计算:（1）（-2a）3-（-a）·（3a）2.
（2）ab2c·（-0.5ab）2·（-2bc2）3.
5.计算:
（1）4t3·t5＋（2t4）2-7t8；
（2）2x3·（-x）5-x5·（-x）3.
知识点二 单项式与多项式相乘
6.如果一个三角形的一边长为2x2y＋xy-y2，该边上的高为6xy，那么这个三角形的面积为（ ）
A.6x3y2＋3x2y2-3xy3 B.6x2y2＋3xy-3xy2 C.6x2y2＋3x2y2-y2 D.6x2y＋3x2y2
7.下列计算正确的是（ ）
A.-2a·（3ab-2a2b）＝-6a2b-4a3b B.2ab2·（-a2＋2b2-1）＝-4a3b4
C.abc·（3a2b-2ab2）＝3a3b2-2a2b3 D.（ab）2·（3ab2-c）＝3a3b4-a2b2c
8.张雪同学遇到了这样一道题:-3xy·（4y-2x-1）＝-12xy2＋6x2y＋_______，则横线处应填写（ ）
A.3xy B.-3xy C.-1 D.1
9.已知ab2＝-1，则-ab（a2b5-ab3-b）的值等于（ ）
A.-1 B.0 C.1 D.无法确定
10.计算:（x＋y）·（xy）＝____________.
11.已知x2＋2x＝-1，则代数式5＋x（x＋2）的值为__________.
12.图中的四边形均为长方形，根据图形的面积关系，写出一个正确的等式:___________.
13.计算：
（1）；
（2）.
14.解方程:
2x（x-1）-x（2x＋3）＝15.
15.数学测验中，李华同学在计算一个多项式乘-2x2时，由于粗心大意，错将乘号看成了加号，得到结果x2-3x＋1，你能帮他把正确答案找出来吗？
知识点三 多项式与多项式相乘
16.计算（a＋1）（a-3）的结果是（ ）
A.a2＋2a-3 B.a2＋2a＋3 C.a2-2a-3 D.a2-4a-3
17.下列计算中，正确的有（ ）
①（2a-3）（3a-1）＝6a2-11a＋3； ②（m＋n）（n＋m）＝m2＋mn＋n2；
③（a-2）（a＋3）＝a2-6； ④（1-a）（1＋a）＝1-a2.
A.4个 B.3个 C.2个 D.1个
18.若（x＋1）（x＋n）＝x2＋mx-2，则m的值为（ ）
A.-1 B.1 C.-2 D.2
19.设多项式A是二项式，B是三项式，则A×B的结果中多项式的项数一定（ ）
A等于5项 B.不多于5项 C.多于6项 D.不多于6项
20.若M＝（x-3）（x-4），N＝（x-1）（x-6），则M与N的大小关系为（ ）
A.M＞N B.M＝N C.M＜N D.由x的取值而定
21.（1）先化简，再求值:
（2x＋1）（x-5）-（3x＋1）（5x-2），其中x＝-1；
（2）解方程:（2x＋3）（x-4）-（x＋2）（x-3）＝x2＋6.
22.若（x2＋mx-8）（x2-3x＋n）的展开式中不含x2和x3项，求m＋n的值.
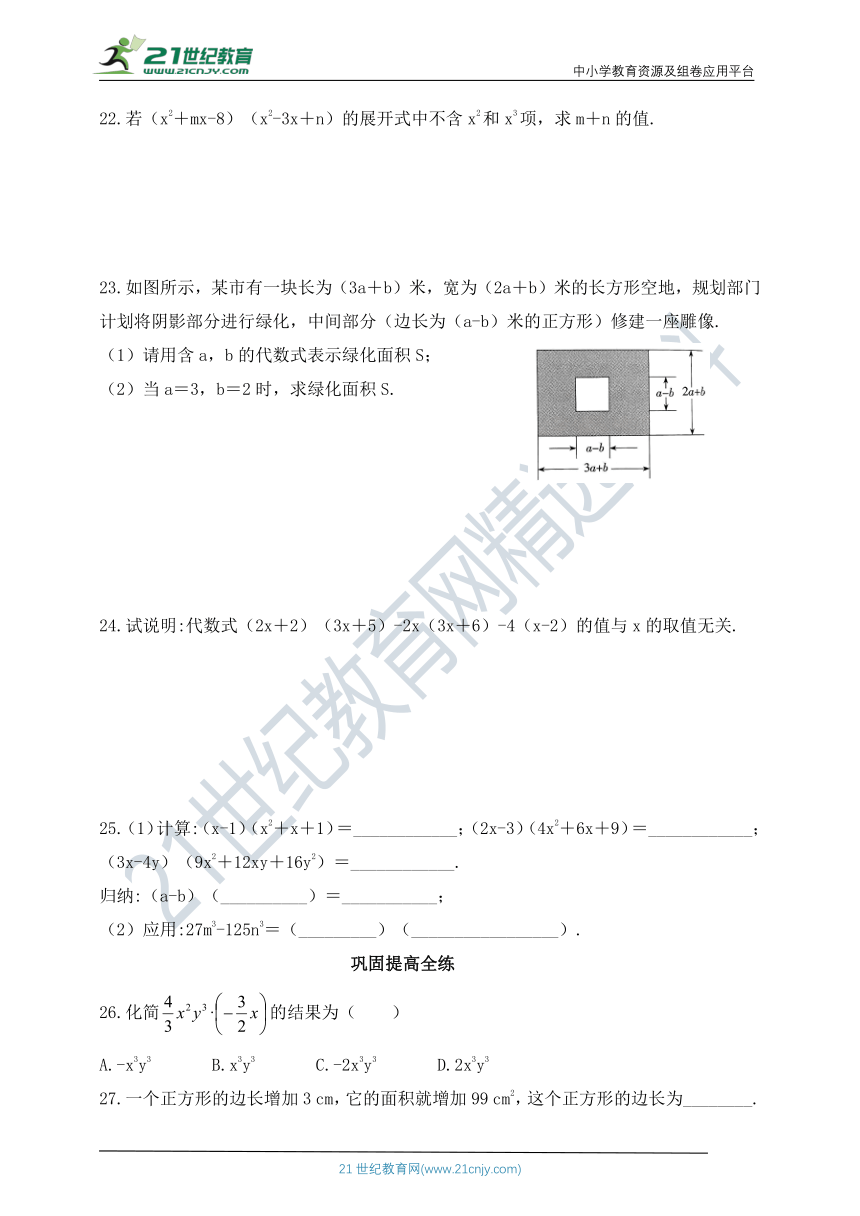
23.如图所示，某市有一块长为（3a＋b）米，宽为（2a＋b）米的长方形空地，规划部门计划将阴影部分进行绿化，中间部分（边长为（a-b）米的正方形）修建一座雕像.
（1）请用含a，b的代数式表示绿化面积S；
（2）当a＝3，b＝2时，求绿化面积S.
24.试说明:代数式（2x＋2）（3x＋5）-2x（3x＋6）-4（x-2）的值与x的取值无关.
25.（1）计算:（x-1）（x2＋x＋1）＝____________；（2x-3）（4x2＋6x＋9）＝____________；（3x-4y）（9x2＋12xy＋16y2）＝____________.
归纳:（a-b）（__________）＝___________；
（2）应用:27m3-125n3＝（_________）（_________________）.
巩固提高全练
26.化简的结果为（ ）
A.-x3y3 B.x3y3 C.-2x3y3 D.2x3y3
27.一个正方形的边长增加3 cm，它的面积就增加99 cm2，这个正方形的边长为________.
28.若a＋b＝3，ab＝2则（a＋1）（b＋1）＝___________.
29.若化简（2x＋m）·（2x-2020）的结果中不含x的一次项，则常数m的值为________.
30.计算:
（1）（-2a2）（3ab2-5ab3）；
（2）（5x＋2y）（3x-2y）.
31.计算2a2·3a4的结果是（ ）
A.5a6 B.5a8 C.6a6 D.6a8
32.计算:x（x2-1）＝（ ）
A.x3-1 B.x3-x C.x3＋x D.x2-x
33.已知m＋n＝mn，则（m-1）（n-1）＝____________.
34.先化简，再求值:
（x＋1）（x-1）＋x（2-x），其中x＝.
35.已知（x＋m）（x＋n）＝x2＋px＋12，m，n为正整数，求p的值.
36.有若张如图①所示的A，B，C三种卡片，A表示边长为m的正方形，B表示边长为n的正方形，C表示长为m、宽为n的长方形.
（1）小明用1张A卡片，4张B卡片，4张C卡片拼成了一个大正方形，这个大正方形的面积为_____________，边长为____________.
（2）小玲想用这三种卡片拼一个如图②所示的长为（2m＋n）、宽为（m＋n）的长方形，需要A，B，C三种卡片各多少张？并在图②的长方形中画出一种拼法.（标上卡片名称）
参考答案
1.A 2.C 3.答案 6x4y
4.解析（1）（-2a）3-（-a）·（3a）2＝-8a3-（-a）·9a2＝-8a3＋9a3＝a3.
（2）ab2c·（-0.5ab）2·（-2bc2）3＝ab2c·0.25a2b2·（-8b3c6）
＝-（×0.25×8）·（a·a2）·（b2·b2·b3）·（c·c6）＝-a3b7c7.
5.解析（1）原式＝4t8＋4t8-7t8＝8t8-7t8＝t8.
（2）原式＝-2x8＋x8＝-x8.
6.A 7.D 8.A 9.C 10.答案x2y＋xy2 11.答案 4
12.答案 2a（a＋b）＝2a2＋2ab（答案不唯一）
13.解析（1）原式＝.
（2）原式＝2x3＋6x2-8x-x3-3x2＝-x3＋3x2-8x.
14.解析 2x（x-1）-x（2x＋3）＝15，2x2-2x-2x2-3x＝15，
整理得-5x＝15，解得x＝-3.
15.解析 设多项式为A，则有A＋（-2x2）＝x2-3x＋1，
所以A＝3x2-3x＋1，（3x2-3x＋1）·（-2x2）＝-6x4＋6x3-2x2.
所以正确答案为-6x4＋6x3-2x2.
16.C 17.C 18.A 19.D 20.A
21.解析（1）（2x＋1）（x-5）-（3x＋1）（5x-2）
＝2x2-10x＋x-5-（15x2-6x＋5x-2）
＝2x2-9x-5-15x2＋x＋2＝-13x2-8x-3.
当x＝-1时，原式＝-13×（-1）2-8×（-1）-3＝-8.
（2）（2x＋3）（x-4）-（x＋2）（x-3）＝x2＋6，
所以2x2-8x＋3x-12-（x2-3x＋2x-6）＝x2＋6，
所以2x2-5x-12-x2＋x＋6＝x2＋6，所以x2-4x-6＝x2＋6，
所以-4x＝12，解得x＝-3.
22.解析 原式＝x4-3x3＋nx2＋mx2-3mx2＋mnx-8x2＋24x-8n
＝x4＋（m-3）x3＋（n-3m-8）x2＋（mn＋24）x-8n，
因为展开式中不含x2和x3项,所以m-3＝0且n-3m-8＝0，
解得m＝3，n＝17，故m＋n＝20.
23.解析 （1）长方形空地的面积为（3a＋b）（2a＋b）＝（6a2＋5ab＋b2）平方米，
中间部分的面积为（a-b）2＝（a2-2ab＋b2）平方米，
则绿化面积S＝（6a2＋5ab＋b2）-（a2-2ab＋b2）＝（5a2＋7ab）平方米，
即化面积S为（5a2＋7ab）平方米.
（2）当a＝3，b＝2时，S＝5×32＋7×3×2＝87平方米，
即绿化面积S为87平方米.
24.解析 因为（2x＋2）（3x＋）-2x（3x＋6）-4（x-2）
＝6x2＋10x＋6x＋10-6x2-12x-4x＋8＝18
所以代数式的值与x的取值无关.
25.解析 （1）（x-1）（x2＋x＋1）＝x3＋x2＋x-x2-x-1＝x3-1.
（2x-3）（4x2＋6x＋9）＝8x3＋12x2＋18x-12x2-18x-27＝8x3-27.
（3x-4y）（9x2＋12xy＋16y2）＝27x3＋36x2y＋48xy2-36x2y-48xy2-64y3＝27x3-64y3.
归纳:（a-b）（a2＋ab＋b2）＝a3-b3.
（2）27m3-125n3＝（3m-5n）（9m2＋15mn＋25n2）.
26.C 27.答案 15 cm 28.答案 6 29.答案 2020
30.解析（1）原式＝-6a3b2＋10a3b3
（2）原式＝15x2-10xy＋6xy-4y2＝15x2-4xy-4y2.
31.C 32.B 33.答案 1
34.解析 原式＝x2-1＋2x-x2＝2x-1，当x＝时，原式＝2×-1＝0.
35.解析 因为（x＋m）（x＋n）＝x2＋px＋12，
所以x2＋（m＋n）x＋mn＝x2＋px＋12.
所以p＝m＋n，mn＝12.）:（1÷×）
因为m，n为正整数，所以m＝1，n＝12或m＝2，n＝6或m＝3，n＝4或m＝12，n＝1或m＝6，n＝2或m＝4，n＝3.
所以p＝13或p＝8或p＝7.
36.解析 （1）m2＋4mn＋4n2； m＋2n.
（2）因为（2m＋n）（m＋n）＝2m2＋3mn＋n2，
所以需要2张A卡片，1张B卡片，3张C卡片
如图所示（拼法不唯一）:
_21?????????è?????(www.21cnjy.com)_