2020-2021年北师大版七年级数学下册 4.4 用尺规作三角形课件(35张)
文档属性
| 名称 | 2020-2021年北师大版七年级数学下册 4.4 用尺规作三角形课件(35张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 542.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 00:00:00 | ||
图片预览










文档简介
第四章 三角形
用尺规作三角形
学习目标
1.(课标)会利用基本作图作三角形:已知三边、两边及其夹角、两角及其夹边作三角形.
2.了解作图方法的合理性.
1.尺规作图的定义:
在几何作图中,把用没有刻度的直尺和圆规作图,简称尺
规作图.
注意:尺规作图指的是只用没有刻度的直尺和圆规两种工具.
2.基本作图:
①作一条线段等于已知线段;②作一个角等于已知角;
③作一个角的平分线;④作线段的垂直平分线;
⑤过一点作已知直线的垂线.
1
基本尺规作图包括:
①作一条线段等于____________;
②作一个角等于____________;
③作一个角的_____________;
④作一条线段的______________;
⑤过一点作已知直线的________.
已知线段
已知角
平分线
垂直平分线
垂线
尺规作图的画图工具是( )
A.刻度尺、圆规
B.三角板和量角器
C.直尺和量角器
D.没有刻度的直尺和圆规
2
D
知识要点
知识点一:根据“SAS”作三角形
?(1)已知三角形的两边及其夹角,求作这个三角形是利用三角形全等的条件“SAS”来作图.
?(2)作图方法有两种:
①先作角,再截取两边;
②先作一边(作一边等于已知线段),然后作角,最后再截取另一边.
对点训练
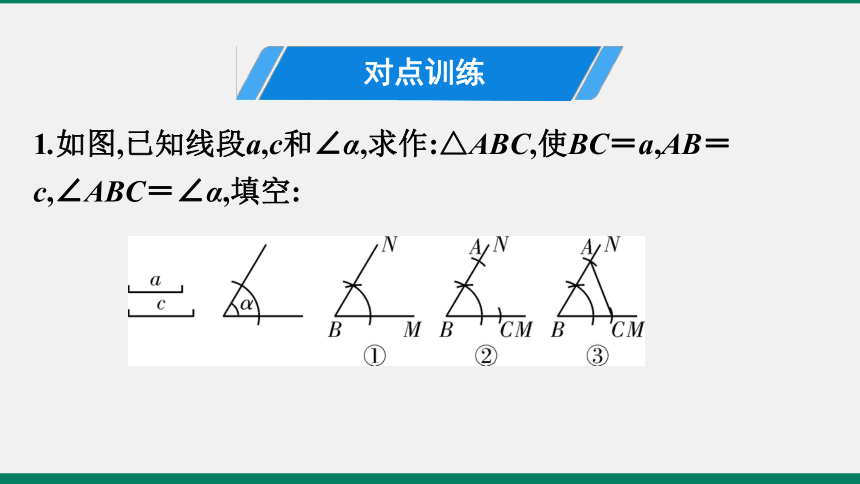
1.如图,已知线段a,c和∠α,求作:△ABC,使BC=a,AB=c,∠ABC=∠α,填空:
(1)如图①,作∠MBN= ;?
(2)如图②,在射线BM上截取BC= ,在射线BN上截取BA= ;?
(3)如图③,连接AC,△ABC就是 .?
所求作的三角形
c
a
∠α
本题考查学生利用基本作图方法作三角形的能力,
以及准确运用简练的几何语言表达作图方法与步骤的
能力,解题的关键是运用转化思想,将图形语言转化
为几何语言.解答时,也可用尺规按图形中所给的信
息进行操作,进而理解其作法的用意.
小 结
知识点二:根据“ASA”作三角形
?
(1)已知三角形的两角及其夹边,求作这个三角形是利用三角形全等的条件“ASA”来作图.
?
(2)作图方法有两种:
①先作一个角,再作边,最后再作另一个角;
②先作一边,再作两个角.
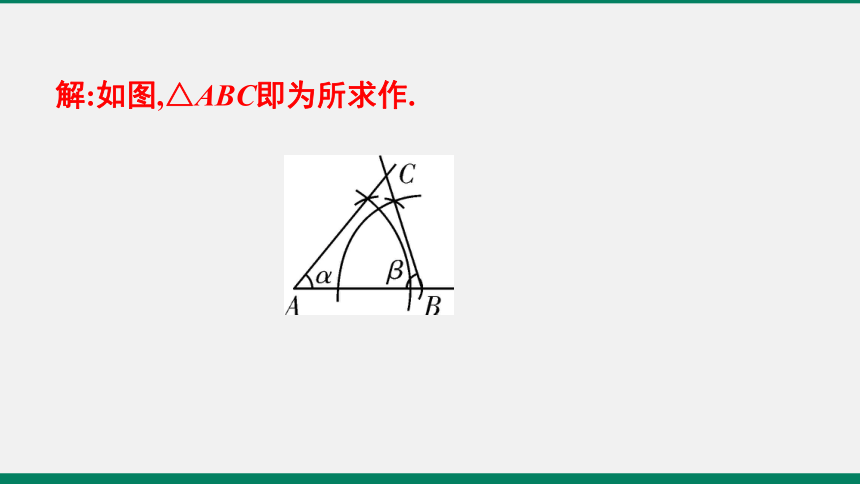
2.已知三角形的两个角分别是∠α和∠β,这两角所夹的边等于a,如图所示,求作△ABC,使∠A=∠α,∠B=∠β,AB=a.(不写作法,保留作图痕迹)
解:如图,△ABC即为所求作.
3.如图,已知:∠α,∠β=90°,线段a.
求作:Rt△ABC,使∠B=∠α,∠C=∠β,BC=2a.
(不写作法,保留作图痕迹)
根据题意先画出草图,可
知原题可转化为已知两角
及其夹边,求作三角形的
问题.先画线段BC=2a,再以B为顶点,BC为一边,
作∠B=∠α,以C为顶点,BC为一边,在CB的同
侧,作∠C=∠β,交∠B的另一边于A点.
导引:
如图所示,△ABC即为所求.
解:
此题所作三角形的一边长度为已知线段a的2倍,
这一点审题时要稍加注意.此外,此题还可以先作
∠B=∠α,然后以B为一端点,截取BC=2a,最后以
C为顶点,CB为一边,在CB的同侧作∠C=∠β,交
∠B的另一边于A点,这样所成的△ABC也为所求.
小 结
知识点三:根据“SSS”作三角形
?
(1)已知三角形的三条边,求作这个三角形是利用三角形全等的条件“SSS”来作图.
?
(2)作图方法:先作出一条边(即先确定三角形的两个顶点),再用两条弧的交点确定第二个顶点.
4.已知:线段a,b,c如图所示.求作:△ABC,使AB=c,AC=b,BC=a.补全下表作图.(不写作法,保留作图痕迹)
作法
图形
(1)作一条线段BC=a;
?
(2)分别以点B,C为圆心,以c,b的长为半径画弧,两弧交于点A;
?
(3)连接AB,AC,△ABC就是所求作的三角形
?
5.如图,已知线段a,b,m,求作△ABC,使BC=2a,AC=b,且BC边上的中线AD=m.
解:
作法:
(1)作△ADC,使AC=b,AD=m,
DC=a;
(2)作BD=a;
(3)连接AB,则△ABC即为
所求作的三角形,如图
所示.
本题中,已知,求作已经给出,但该作图题较复
杂,我们可以先进行分析:假设△ABC已经作出,且
满足BC=2a,AC=b,BC边上的中线AD=m,不难发
现△ADC的三边已知,可以先作出△ADC,因为D是
BC的中点,所以在△ADC确定后就可以确定B点的位
置,从而可以作出△ABC,因此我们得出几何作图的
一般步骤:
小 结
(1)已知,即将条件具体化;
(2)求作,即具体叙述所作图形应满足的条件;
(3)分析,即寻找作图方法(通常画出草图);
(4)作法,即根据分析所得的作图方法,作出正式图
形,并依次叙述作图过程;
(5)说明,即验证所作图形的正确性.其中(3)在草稿
纸上进行,(5)通常省略不写.
6.如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,则最多可以作出_______个这样的三角形.
4
导引:
如图,以D为圆心,AB长为半径画
弧;以E为圆心,AC长为半径画弧,
两弧相交于两点(DE上、下各一个),
分别与点D,E连接后,可得到两个
三角形;以D为圆心,AC长为半径
画弧;以E为圆心,AB长为半径画弧,两弧相交于两
点(DE上、下各一个),分别与点D,E连接后,可得
到两个三角形.因此最多能作出4个符合要求的三角
形.
这是一道探索型题目.解决这类问题的关键是运
用分类讨论思想分析得出所有可能的情况.
小 结
精典范例
7.已知:线段a和∠α如图所示.求作:△ABC,使AB=AC=a,∠A=∠α.(不写作法,保留作图痕迹)
解:如图,△ABC即为所求作.
变式练习
8.你能用尺规作一个直角三角形,使其两条直角边分别等于已知线段a,b吗?(不写作法,保留作图痕迹)
解:如图,Rt△ABC即为所求作.
9.已知:∠α,∠β和线段a,如图所示.求作:△ABC,使BC=2a,∠B=∠α,∠C=2∠β.(不写作法,保留作图痕迹)
解:如图,△ABC即为所求作.
10.(创新题)小明不小心在一个三角形上洒了一片墨水,请用尺规帮小明重新画一个三角形使它与原来的三角形完全相同.(保留作图痕迹,不写作法)
解:按尺规作图的要求,正确作出△ABC如图所示.
11.如图,已知线段a,用尺规作出△ABC,使AB=a,BC=AC=2a.
(2)分别以 、 为圆心,以 为半径画弧,两弧交于点C;?
(3)连接 、 ,则△ABC就是所求作的三角形;?
(4)请按(1)(2)(3)的作图步骤,作出△ABC.
解:(4)如图:
BC
AC
2a
B
A
作法:(1)作一条线段AB= ;?
a
★12.利用尺规,用三种不同的方法作一个三角形与已知三角形ABC全等,并简要说明理由.(同种理由视为是同一种方法)
解:如图,△DEF为所作.
(SSS)
(SAS)
(ASA)
13.(新题速递)(2020邢台一模)下面是黑板上出示的的尺规作图题,符号代表的内容是( )
如图,已知∠AOB,求作:∠DEF,使∠DEF=∠AOB.
作法:(1)以 为圆心,任意长为半径画弧,分别交OA,OB于点P,Q;
(2)作射线EG,并以点E为圆心, 长为半径画弧交EG于点D;
(3)以点D为圆心, 长为半径画弧,交(2)步中所画弧于点F;
(4)作 ,∠DEF即为所求作的角.
答案: D
1.尺规作图的定义:
在几何作图中,把用没有刻度的直尺和圆规作图,简称尺作图.
2.常见的几种尺规作图:
基本作图:
①作一条线段等于已知线段;
②作一个角等于已知角;
③作一个角的平分线;
④作线段的垂直平分线;
⑤过一点作已知直线的垂线.
总结
用尺规作三角形
学习目标
1.(课标)会利用基本作图作三角形:已知三边、两边及其夹角、两角及其夹边作三角形.
2.了解作图方法的合理性.
1.尺规作图的定义:
在几何作图中,把用没有刻度的直尺和圆规作图,简称尺
规作图.
注意:尺规作图指的是只用没有刻度的直尺和圆规两种工具.
2.基本作图:
①作一条线段等于已知线段;②作一个角等于已知角;
③作一个角的平分线;④作线段的垂直平分线;
⑤过一点作已知直线的垂线.
1
基本尺规作图包括:
①作一条线段等于____________;
②作一个角等于____________;
③作一个角的_____________;
④作一条线段的______________;
⑤过一点作已知直线的________.
已知线段
已知角
平分线
垂直平分线
垂线
尺规作图的画图工具是( )
A.刻度尺、圆规
B.三角板和量角器
C.直尺和量角器
D.没有刻度的直尺和圆规
2
D
知识要点
知识点一:根据“SAS”作三角形
?(1)已知三角形的两边及其夹角,求作这个三角形是利用三角形全等的条件“SAS”来作图.
?(2)作图方法有两种:
①先作角,再截取两边;
②先作一边(作一边等于已知线段),然后作角,最后再截取另一边.
对点训练
1.如图,已知线段a,c和∠α,求作:△ABC,使BC=a,AB=c,∠ABC=∠α,填空:
(1)如图①,作∠MBN= ;?
(2)如图②,在射线BM上截取BC= ,在射线BN上截取BA= ;?
(3)如图③,连接AC,△ABC就是 .?
所求作的三角形
c
a
∠α
本题考查学生利用基本作图方法作三角形的能力,
以及准确运用简练的几何语言表达作图方法与步骤的
能力,解题的关键是运用转化思想,将图形语言转化
为几何语言.解答时,也可用尺规按图形中所给的信
息进行操作,进而理解其作法的用意.
小 结
知识点二:根据“ASA”作三角形
?
(1)已知三角形的两角及其夹边,求作这个三角形是利用三角形全等的条件“ASA”来作图.
?
(2)作图方法有两种:
①先作一个角,再作边,最后再作另一个角;
②先作一边,再作两个角.
2.已知三角形的两个角分别是∠α和∠β,这两角所夹的边等于a,如图所示,求作△ABC,使∠A=∠α,∠B=∠β,AB=a.(不写作法,保留作图痕迹)
解:如图,△ABC即为所求作.
3.如图,已知:∠α,∠β=90°,线段a.
求作:Rt△ABC,使∠B=∠α,∠C=∠β,BC=2a.
(不写作法,保留作图痕迹)
根据题意先画出草图,可
知原题可转化为已知两角
及其夹边,求作三角形的
问题.先画线段BC=2a,再以B为顶点,BC为一边,
作∠B=∠α,以C为顶点,BC为一边,在CB的同
侧,作∠C=∠β,交∠B的另一边于A点.
导引:
如图所示,△ABC即为所求.
解:
此题所作三角形的一边长度为已知线段a的2倍,
这一点审题时要稍加注意.此外,此题还可以先作
∠B=∠α,然后以B为一端点,截取BC=2a,最后以
C为顶点,CB为一边,在CB的同侧作∠C=∠β,交
∠B的另一边于A点,这样所成的△ABC也为所求.
小 结
知识点三:根据“SSS”作三角形
?
(1)已知三角形的三条边,求作这个三角形是利用三角形全等的条件“SSS”来作图.
?
(2)作图方法:先作出一条边(即先确定三角形的两个顶点),再用两条弧的交点确定第二个顶点.
4.已知:线段a,b,c如图所示.求作:△ABC,使AB=c,AC=b,BC=a.补全下表作图.(不写作法,保留作图痕迹)
作法
图形
(1)作一条线段BC=a;
?
(2)分别以点B,C为圆心,以c,b的长为半径画弧,两弧交于点A;
?
(3)连接AB,AC,△ABC就是所求作的三角形
?
5.如图,已知线段a,b,m,求作△ABC,使BC=2a,AC=b,且BC边上的中线AD=m.
解:
作法:
(1)作△ADC,使AC=b,AD=m,
DC=a;
(2)作BD=a;
(3)连接AB,则△ABC即为
所求作的三角形,如图
所示.
本题中,已知,求作已经给出,但该作图题较复
杂,我们可以先进行分析:假设△ABC已经作出,且
满足BC=2a,AC=b,BC边上的中线AD=m,不难发
现△ADC的三边已知,可以先作出△ADC,因为D是
BC的中点,所以在△ADC确定后就可以确定B点的位
置,从而可以作出△ABC,因此我们得出几何作图的
一般步骤:
小 结
(1)已知,即将条件具体化;
(2)求作,即具体叙述所作图形应满足的条件;
(3)分析,即寻找作图方法(通常画出草图);
(4)作法,即根据分析所得的作图方法,作出正式图
形,并依次叙述作图过程;
(5)说明,即验证所作图形的正确性.其中(3)在草稿
纸上进行,(5)通常省略不写.
6.如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,则最多可以作出_______个这样的三角形.
4
导引:
如图,以D为圆心,AB长为半径画
弧;以E为圆心,AC长为半径画弧,
两弧相交于两点(DE上、下各一个),
分别与点D,E连接后,可得到两个
三角形;以D为圆心,AC长为半径
画弧;以E为圆心,AB长为半径画弧,两弧相交于两
点(DE上、下各一个),分别与点D,E连接后,可得
到两个三角形.因此最多能作出4个符合要求的三角
形.
这是一道探索型题目.解决这类问题的关键是运
用分类讨论思想分析得出所有可能的情况.
小 结
精典范例
7.已知:线段a和∠α如图所示.求作:△ABC,使AB=AC=a,∠A=∠α.(不写作法,保留作图痕迹)
解:如图,△ABC即为所求作.
变式练习
8.你能用尺规作一个直角三角形,使其两条直角边分别等于已知线段a,b吗?(不写作法,保留作图痕迹)
解:如图,Rt△ABC即为所求作.
9.已知:∠α,∠β和线段a,如图所示.求作:△ABC,使BC=2a,∠B=∠α,∠C=2∠β.(不写作法,保留作图痕迹)
解:如图,△ABC即为所求作.
10.(创新题)小明不小心在一个三角形上洒了一片墨水,请用尺规帮小明重新画一个三角形使它与原来的三角形完全相同.(保留作图痕迹,不写作法)
解:按尺规作图的要求,正确作出△ABC如图所示.
11.如图,已知线段a,用尺规作出△ABC,使AB=a,BC=AC=2a.
(2)分别以 、 为圆心,以 为半径画弧,两弧交于点C;?
(3)连接 、 ,则△ABC就是所求作的三角形;?
(4)请按(1)(2)(3)的作图步骤,作出△ABC.
解:(4)如图:
BC
AC
2a
B
A
作法:(1)作一条线段AB= ;?
a
★12.利用尺规,用三种不同的方法作一个三角形与已知三角形ABC全等,并简要说明理由.(同种理由视为是同一种方法)
解:如图,△DEF为所作.
(SSS)
(SAS)
(ASA)
13.(新题速递)(2020邢台一模)下面是黑板上出示的的尺规作图题,符号代表的内容是( )
如图,已知∠AOB,求作:∠DEF,使∠DEF=∠AOB.
作法:(1)以 为圆心,任意长为半径画弧,分别交OA,OB于点P,Q;
(2)作射线EG,并以点E为圆心, 长为半径画弧交EG于点D;
(3)以点D为圆心, 长为半径画弧,交(2)步中所画弧于点F;
(4)作 ,∠DEF即为所求作的角.
答案: D
1.尺规作图的定义:
在几何作图中,把用没有刻度的直尺和圆规作图,简称尺作图.
2.常见的几种尺规作图:
基本作图:
①作一条线段等于已知线段;
②作一个角等于已知角;
③作一个角的平分线;
④作线段的垂直平分线;
⑤过一点作已知直线的垂线.
总结
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
