2020--2021学年人教版数学九年级下册第二十七章 《相似》 常考题强化练习(四) (Word版 无答案)
文档属性
| 名称 | 2020--2021学年人教版数学九年级下册第二十七章 《相似》 常考题强化练习(四) (Word版 无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 167.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 22:09:16 | ||
图片预览


文档简介
2020--2021学年九年级下册数学第二十七章
《相似》
常考题强化练习(四)
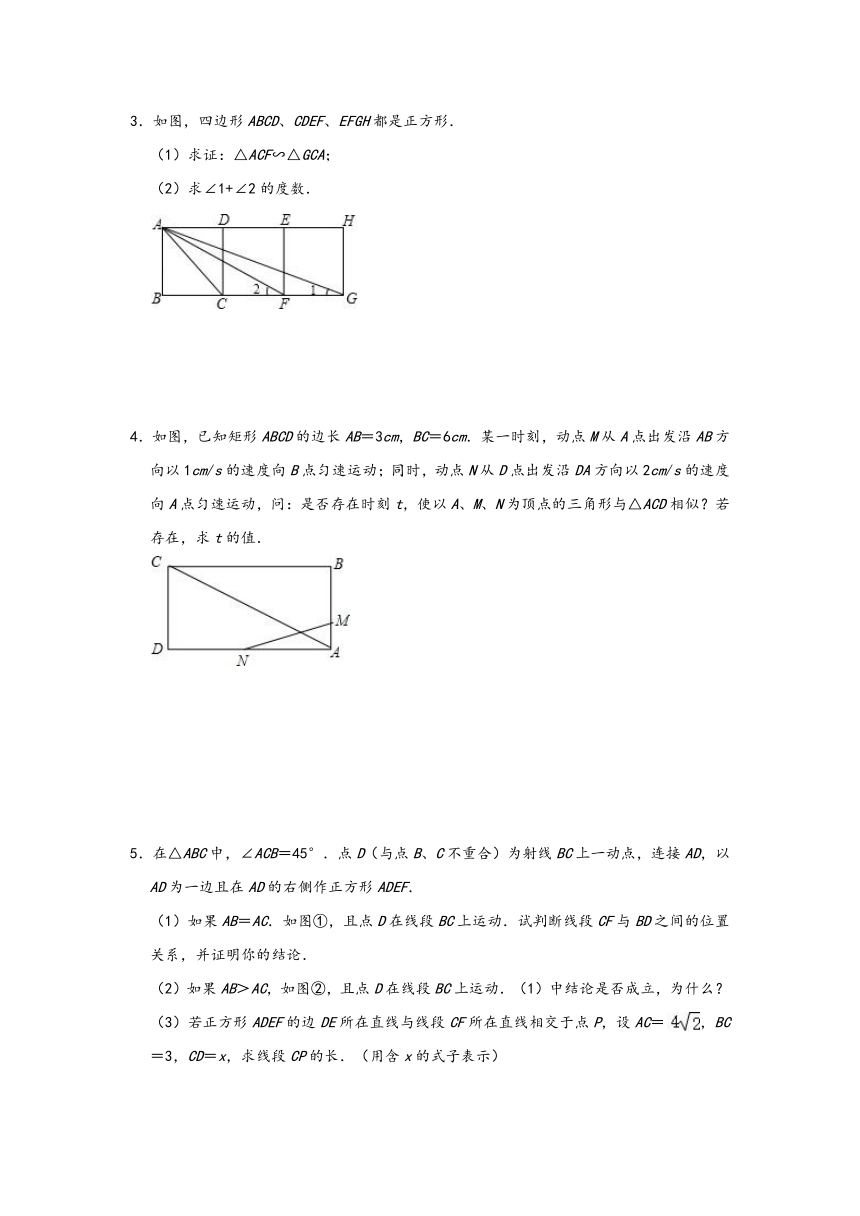
1.《铁血红安》在中央一台热播后,吸引了众多游客前往影视基地游玩.某天小明站在地面上给站在城楼上的小亮照相时发现:他的眼睛、凉亭顶端、小亮头顶三点恰好在一条直线上(如图).已知小明的眼睛离地面1.65米,凉亭顶端离地面2米,小明到凉亭的距离为2米,凉亭离城楼底部的距离为40米,小亮身高1.7米.请根据以上数据求出城楼的高度.
2.阅读理解:给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半,则这个矩形是给定矩形的“减半”矩形.如图,矩形A1B1C1D1是矩形ABCD的“减半”矩形.
请你解决下列问题:
(1)当矩形的长和宽分别为1,2时,它是否存在“减半”矩形?请作出判断,并请说明理由;
(2)边长为a的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,说明理由.
3.如图,四边形ABCD、CDEF、EFGH都是正方形.
(1)求证:△ACF∽△GCA;
(2)求∠1+∠2的度数.
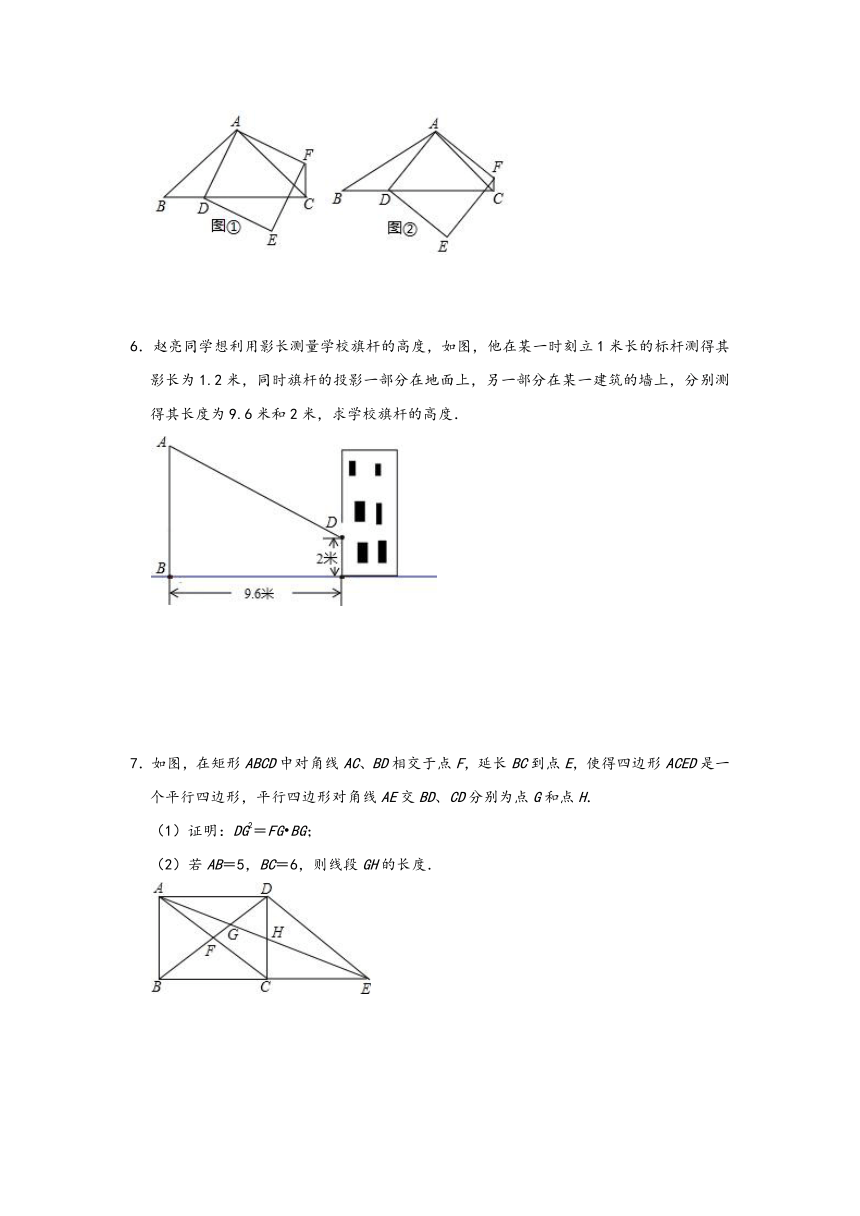
4.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:是否存在时刻t,使以A、M、N为顶点的三角形与△ACD相似?若存在,求t的值.
5.在△ABC中,∠ACB=45°.点D(与点B、C不重合)为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC.如图①,且点D在线段BC上运动.试判断线段CF与BD之间的位置关系,并证明你的结论.
(2)如果AB>AC,如图②,且点D在线段BC上运动.(1)中结论是否成立,为什么?
(3)若正方形ADEF的边DE所在直线与线段CF所在直线相交于点P,设AC=,BC=3,CD=x,求线段CP的长.(用含x的式子表示)
6.赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,求学校旗杆的高度.
7.如图,在矩形ABCD中对角线AC、BD相交于点F,延长BC到点E,使得四边形ACED是一个平行四边形,平行四边形对角线AE交BD、CD分别为点G和点H.
(1)证明:DG2=FG?BG;
(2)若AB=5,BC=6,则线段GH的长度.
8.如图,在△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE.
(1)求证:△ABC∽△ADE;
(2)判断△ABD与△ACE是否相似?并证明.
9.如图,在Rt△ABC中,∠ACB=90°AC=10cm,BC=15cm,点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动,点P,Q分另从起点同时出发,移动到某一位置时所需时间为t秒.
(1)当t=4时,求线段PQ的长度;
(2)当t为何值时,△PQC的面积等于16cm2?
(3)点O为AB的中点,连接OC,能否使得PQ⊥OC?若能,求出t值;若不能,说明理由.
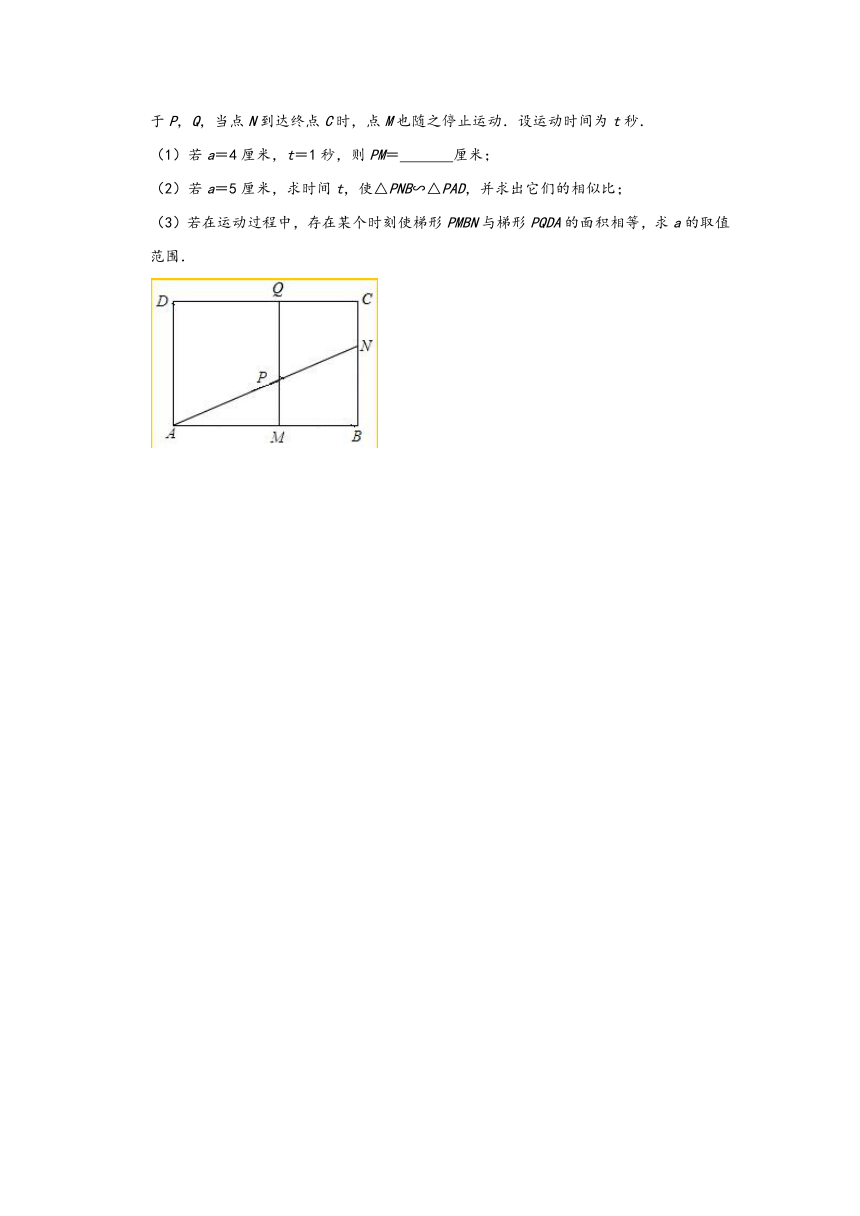
10.如图,在矩形ABCD中,AD=3厘米,AB=a厘米(a>3),动点M,N同时从B点出发,分别沿BA,BC方向运动,速度都是1厘米/秒,过M作直线垂直于AB,分别交AN,CD于P,Q,当点N到达终点C时,点M也随之停止运动.设运动时间为t秒.
(1)若a=4厘米,t=1秒,则PM=
厘米;
(2)若a=5厘米,求时间t,使△PNB∽△PAD,并求出它们的相似比;
(3)若在运动过程中,存在某个时刻使梯形PMBN与梯形PQDA的面积相等,求a的取值范围.
参考答案
1.解:过点A作AM⊥EF于点M,交CD于点N,
由题意可得:AN=2m,CN=2﹣1.65=0.35(m),MN=40m,
∵CN∥EM,
∴△ACN∽△AEM,
∴=,
∴=,
解得:EM=7.35,
∵AB=MF=1.65m,
故城楼的高度为:7.35+1.65﹣1.7=7.3(米),
答:城楼的高度为7.3m.
2.解:(1)不存在.(1分)
假设存在,不妨设“减半”矩形的长和宽分别为x、y,
则,(3分)
由①得:y=﹣x③,
把③代入②得:x2﹣x+1=0,
b2﹣4ac=﹣4<0,(5分)
所以不存在;
(2)不存在.(6分)
因为两个正方形是相似图形,当它们的周长比为时,面积比必定是,
所以正方形不存在“减半”正方形.(10分)
3.(1)证明:可设正方形的边长为a,则AC=a,
∴==,
又∵∠ACF=∠GCA,
∴△ACF∽△GCA;
(2)解:由(1)得:△ACF∽△GCA,
∴∠1=∠CAF,
∴∠1+∠2=∠CAF+∠2=∠ACB=45°.
4.解:当△ACD∽△MNA时,
则,即,
∴36﹣12t=3t.
∴t=2.4.
当△ACD∽△NMA时,则,即.
∴6t=18﹣6t.
∴t=1.5.
答:存在,t为2.4;1.5.
5.解:(1)CF与BD位置关系是垂直;
证明如下:
∵AB=AC,∠ACB=45°,
∴∠ABC=45°.
由正方形ADEF得AD=AF,
∵∠DAF=∠BAC=90°,
∴∠DAB=∠FAC,
∴△DAB≌△FAC(SAS),
∴∠ACF=∠ABD.
∴∠BCF=∠ACB+∠ACF=90°.
∴CF⊥BC.
∴CF⊥BD.
(2)AB>AC时,CF⊥BD的结论成立.
理由是:
过点A作GA⊥AC交BC于点G,
∵∠ACB=45°,
∴∠AGD=45°,
∴AC=AG,
同理可证:△GAD≌△CAF
∴∠ACF=∠AGD=45°,∠BCF=∠ACB+∠ACF=90°,
即CF⊥BD.
(3)过点A作AQ⊥BC交CB的延长线于点Q,
①点D在线段BC上运动时,
∵∠BCA=45°,可求出AQ=CQ=4.
∴DQ=4﹣x,△AQD∽△DCP,
∴,
∴,
∴.
②点D在线段BC延长线上运动时,
∵∠BCA=45°,
∴AQ=CQ=4,
∴DQ=4+x.
过A作AQ⊥BC,
∴∠Q=∠FAD=90°,
∵∠C′AF=∠C′CD=90°,∠AC′F=∠CC′D,
∴∠ADQ=∠AFC′,
则△AQD∽△AC′F.
∴CF⊥BD,
∴△AQD∽△DCP,
∴,
∴,
∴.
6.解:作DE⊥AB于点E,
根据题意得:=,
=,
解得:AE=8米.
则AB=AE+BE=8+2=10米.
即旗杆的高度为10米.
7.解:(1)证明:∵ABCD是矩形,且AD∥BC,
∴△ADG∽△EBG.
∴=.
又∵△AGF∽△EGD,
∴=.
∴=.
∴DG2=FG?BG.
(2)∵ACED为平行四边形,AE,CD相交点H,
∴DH=DC=AB=.
∴在直角三角形ADH中,AH2=AD2+DH2
∴AH=.
又∵△ADG∽△EBG,
∴==.
∴AG=GE=×AE=×13=.
∴GH=AH﹣AG=﹣=.
8.证明:(1)∵∠BAD=∠CAE,
∴∠BAC=∠DAE,
∵∠ABC=∠ADE,
∴△ABC∽△ADE.
(2)△ABD∽△ACE.
证明:由(1)知△ABC∽△ADE,
∴,
∴AB×AE=AC×AD,
∴,
∵∠BAD=∠CAE,
∴△ABD∽△ACE.
9.解:(1)当t=4时,
∵点P从A出发沿AC向C点以1厘米/秒的速度匀速移动,点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动,
∴AP=4cm,PC=AC﹣AP=6cm、CQ=2×4=8cm,
∴PQ==10cm;
(2)∵AP=t,PC=AC﹣AP=10﹣t、CQ=2t,
∴S△PQC=PC×CQ=t(10﹣t)=16,
∴t1=2,t2=8,
当t=8时,CQ=2t=16>15,∴舍去,
∴当t=2时,△PQC的面积等于16cm2;
(3)能够使得PQ⊥OC,如图所示:
∵点O为AB的中点,∠ACB=90°,
∴OA=OB=OC(直角三角形斜边上中线定理),
∴∠A=∠OCA,
而∠OCA+∠QPC=90°,∠A+∠B=90°,
∴∠B=∠QPC,又∠ACB=∠PCQ=90°,
∴△ABC∽△QPC,
∴,
∴,
∴t=2.5s.
∴当t=2.5s时,PQ⊥OC.
10.解:(1)由题意知,当t=1秒时,BN=BM=1,
∵a=4厘米,∴AM=3,
又∵PM⊥AB,
∴△APM∽△ANB,
∴,
即,
解得,PM=;
(2)如图示,作出△PNB和△PAD,则BM和AM分别是它们的高,
若△PNB∽△PAD,则,即,解得,t=2.
即t=2时,△PNB∽△PAD,相似比为.
(3)设BN=x,则0≤x≤3,则BM=x,
由(1)知,△APM∽△ANB,∴,∴,
∴,
所以由题意得,=,
解得x=,所以0≤≤3,解得0≤a≤6.
又∵a>3,
∴a的范围是3<a≤6.
补充:设BN=BM=x,则PM=,
使梯形PMBN和梯形PQDN面积相等,由(3)得3<a≤6;
若它们的面积都等于梯形PQCN的面积,
∴S梯形PMBN=S矩形BCQM
即[+x]?t=?3?t,
解得t=a,a>3,
∴t=a,
而0≤t≤3,
∴a>3,
所以a的范围是3<a≤6.
《相似》
常考题强化练习(四)
1.《铁血红安》在中央一台热播后,吸引了众多游客前往影视基地游玩.某天小明站在地面上给站在城楼上的小亮照相时发现:他的眼睛、凉亭顶端、小亮头顶三点恰好在一条直线上(如图).已知小明的眼睛离地面1.65米,凉亭顶端离地面2米,小明到凉亭的距离为2米,凉亭离城楼底部的距离为40米,小亮身高1.7米.请根据以上数据求出城楼的高度.
2.阅读理解:给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半,则这个矩形是给定矩形的“减半”矩形.如图,矩形A1B1C1D1是矩形ABCD的“减半”矩形.
请你解决下列问题:
(1)当矩形的长和宽分别为1,2时,它是否存在“减半”矩形?请作出判断,并请说明理由;
(2)边长为a的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,说明理由.
3.如图,四边形ABCD、CDEF、EFGH都是正方形.
(1)求证:△ACF∽△GCA;
(2)求∠1+∠2的度数.
4.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:是否存在时刻t,使以A、M、N为顶点的三角形与△ACD相似?若存在,求t的值.
5.在△ABC中,∠ACB=45°.点D(与点B、C不重合)为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC.如图①,且点D在线段BC上运动.试判断线段CF与BD之间的位置关系,并证明你的结论.
(2)如果AB>AC,如图②,且点D在线段BC上运动.(1)中结论是否成立,为什么?
(3)若正方形ADEF的边DE所在直线与线段CF所在直线相交于点P,设AC=,BC=3,CD=x,求线段CP的长.(用含x的式子表示)
6.赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,求学校旗杆的高度.
7.如图,在矩形ABCD中对角线AC、BD相交于点F,延长BC到点E,使得四边形ACED是一个平行四边形,平行四边形对角线AE交BD、CD分别为点G和点H.
(1)证明:DG2=FG?BG;
(2)若AB=5,BC=6,则线段GH的长度.
8.如图,在△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE.
(1)求证:△ABC∽△ADE;
(2)判断△ABD与△ACE是否相似?并证明.
9.如图,在Rt△ABC中,∠ACB=90°AC=10cm,BC=15cm,点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动,点P,Q分另从起点同时出发,移动到某一位置时所需时间为t秒.
(1)当t=4时,求线段PQ的长度;
(2)当t为何值时,△PQC的面积等于16cm2?
(3)点O为AB的中点,连接OC,能否使得PQ⊥OC?若能,求出t值;若不能,说明理由.
10.如图,在矩形ABCD中,AD=3厘米,AB=a厘米(a>3),动点M,N同时从B点出发,分别沿BA,BC方向运动,速度都是1厘米/秒,过M作直线垂直于AB,分别交AN,CD于P,Q,当点N到达终点C时,点M也随之停止运动.设运动时间为t秒.
(1)若a=4厘米,t=1秒,则PM=
厘米;
(2)若a=5厘米,求时间t,使△PNB∽△PAD,并求出它们的相似比;
(3)若在运动过程中,存在某个时刻使梯形PMBN与梯形PQDA的面积相等,求a的取值范围.
参考答案
1.解:过点A作AM⊥EF于点M,交CD于点N,
由题意可得:AN=2m,CN=2﹣1.65=0.35(m),MN=40m,
∵CN∥EM,
∴△ACN∽△AEM,
∴=,
∴=,
解得:EM=7.35,
∵AB=MF=1.65m,
故城楼的高度为:7.35+1.65﹣1.7=7.3(米),
答:城楼的高度为7.3m.
2.解:(1)不存在.(1分)
假设存在,不妨设“减半”矩形的长和宽分别为x、y,
则,(3分)
由①得:y=﹣x③,
把③代入②得:x2﹣x+1=0,
b2﹣4ac=﹣4<0,(5分)
所以不存在;
(2)不存在.(6分)
因为两个正方形是相似图形,当它们的周长比为时,面积比必定是,
所以正方形不存在“减半”正方形.(10分)
3.(1)证明:可设正方形的边长为a,则AC=a,
∴==,
又∵∠ACF=∠GCA,
∴△ACF∽△GCA;
(2)解:由(1)得:△ACF∽△GCA,
∴∠1=∠CAF,
∴∠1+∠2=∠CAF+∠2=∠ACB=45°.
4.解:当△ACD∽△MNA时,
则,即,
∴36﹣12t=3t.
∴t=2.4.
当△ACD∽△NMA时,则,即.
∴6t=18﹣6t.
∴t=1.5.
答:存在,t为2.4;1.5.
5.解:(1)CF与BD位置关系是垂直;
证明如下:
∵AB=AC,∠ACB=45°,
∴∠ABC=45°.
由正方形ADEF得AD=AF,
∵∠DAF=∠BAC=90°,
∴∠DAB=∠FAC,
∴△DAB≌△FAC(SAS),
∴∠ACF=∠ABD.
∴∠BCF=∠ACB+∠ACF=90°.
∴CF⊥BC.
∴CF⊥BD.
(2)AB>AC时,CF⊥BD的结论成立.
理由是:
过点A作GA⊥AC交BC于点G,
∵∠ACB=45°,
∴∠AGD=45°,
∴AC=AG,
同理可证:△GAD≌△CAF
∴∠ACF=∠AGD=45°,∠BCF=∠ACB+∠ACF=90°,
即CF⊥BD.
(3)过点A作AQ⊥BC交CB的延长线于点Q,
①点D在线段BC上运动时,
∵∠BCA=45°,可求出AQ=CQ=4.
∴DQ=4﹣x,△AQD∽△DCP,
∴,
∴,
∴.
②点D在线段BC延长线上运动时,
∵∠BCA=45°,
∴AQ=CQ=4,
∴DQ=4+x.
过A作AQ⊥BC,
∴∠Q=∠FAD=90°,
∵∠C′AF=∠C′CD=90°,∠AC′F=∠CC′D,
∴∠ADQ=∠AFC′,
则△AQD∽△AC′F.
∴CF⊥BD,
∴△AQD∽△DCP,
∴,
∴,
∴.
6.解:作DE⊥AB于点E,
根据题意得:=,
=,
解得:AE=8米.
则AB=AE+BE=8+2=10米.
即旗杆的高度为10米.
7.解:(1)证明:∵ABCD是矩形,且AD∥BC,
∴△ADG∽△EBG.
∴=.
又∵△AGF∽△EGD,
∴=.
∴=.
∴DG2=FG?BG.
(2)∵ACED为平行四边形,AE,CD相交点H,
∴DH=DC=AB=.
∴在直角三角形ADH中,AH2=AD2+DH2
∴AH=.
又∵△ADG∽△EBG,
∴==.
∴AG=GE=×AE=×13=.
∴GH=AH﹣AG=﹣=.
8.证明:(1)∵∠BAD=∠CAE,
∴∠BAC=∠DAE,
∵∠ABC=∠ADE,
∴△ABC∽△ADE.
(2)△ABD∽△ACE.
证明:由(1)知△ABC∽△ADE,
∴,
∴AB×AE=AC×AD,
∴,
∵∠BAD=∠CAE,
∴△ABD∽△ACE.
9.解:(1)当t=4时,
∵点P从A出发沿AC向C点以1厘米/秒的速度匀速移动,点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动,
∴AP=4cm,PC=AC﹣AP=6cm、CQ=2×4=8cm,
∴PQ==10cm;
(2)∵AP=t,PC=AC﹣AP=10﹣t、CQ=2t,
∴S△PQC=PC×CQ=t(10﹣t)=16,
∴t1=2,t2=8,
当t=8时,CQ=2t=16>15,∴舍去,
∴当t=2时,△PQC的面积等于16cm2;
(3)能够使得PQ⊥OC,如图所示:
∵点O为AB的中点,∠ACB=90°,
∴OA=OB=OC(直角三角形斜边上中线定理),
∴∠A=∠OCA,
而∠OCA+∠QPC=90°,∠A+∠B=90°,
∴∠B=∠QPC,又∠ACB=∠PCQ=90°,
∴△ABC∽△QPC,
∴,
∴,
∴t=2.5s.
∴当t=2.5s时,PQ⊥OC.
10.解:(1)由题意知,当t=1秒时,BN=BM=1,
∵a=4厘米,∴AM=3,
又∵PM⊥AB,
∴△APM∽△ANB,
∴,
即,
解得,PM=;
(2)如图示,作出△PNB和△PAD,则BM和AM分别是它们的高,
若△PNB∽△PAD,则,即,解得,t=2.
即t=2时,△PNB∽△PAD,相似比为.
(3)设BN=x,则0≤x≤3,则BM=x,
由(1)知,△APM∽△ANB,∴,∴,
∴,
所以由题意得,=,
解得x=,所以0≤≤3,解得0≤a≤6.
又∵a>3,
∴a的范围是3<a≤6.
补充:设BN=BM=x,则PM=,
使梯形PMBN和梯形PQDN面积相等,由(3)得3<a≤6;
若它们的面积都等于梯形PQCN的面积,
∴S梯形PMBN=S矩形BCQM
即[+x]?t=?3?t,
解得t=a,a>3,
∴t=a,
而0≤t≤3,
∴a>3,
所以a的范围是3<a≤6.
