高一数学 第2课时 子集,真子集、补集(17张PPT)
文档属性
| 名称 | 高一数学 第2课时 子集,真子集、补集(17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 236.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 19:06:08 | ||
图片预览






文档简介
1.复习元素与集合的关系
⑴0___N;
⑵ ____Q;
⑶-1.5____R
∈
?
∈
温故知新
观察下列几组集合,试从集合元素的角度分析集合A与集合B的关系
(1)A={1,2,3},B={1,2,3,4,5}
(2)A=N,B=Q
(3)A={-2,4},
(4)A={x|x为北京人}, B={x|x为中国人}
问题探究一
如果集合A中的任意一个元素都是 集合B的元素,那么集合A称为集合B的子集.
记作 A B(或B A)
B
A
读作:A包含于集合B”,或“集合B包含集合A”.
知识建构
判断集合A是否为集合B的子集,若是则在( )打√,若不是则在( )打×:
①A={1,3,5}, B={1,2,3,4,5,6} ( )
②A={1,3,5}, B={1,3,6,9} ( )
③A={0}, B={x x2+2=0} ( )
④A={a,b,c,d}, B={d,b,c,a} ( )
练习1
思考:以下式子成立吗?
⑴A?A;⑵Φ?A;⑶Φ?Φ.
想一想:
1.A?B与B?A能否同时成立?
你能举出一个例子吗?
集合与集合之间的 “相等”关系:
若A?B且B?A,则A=B.
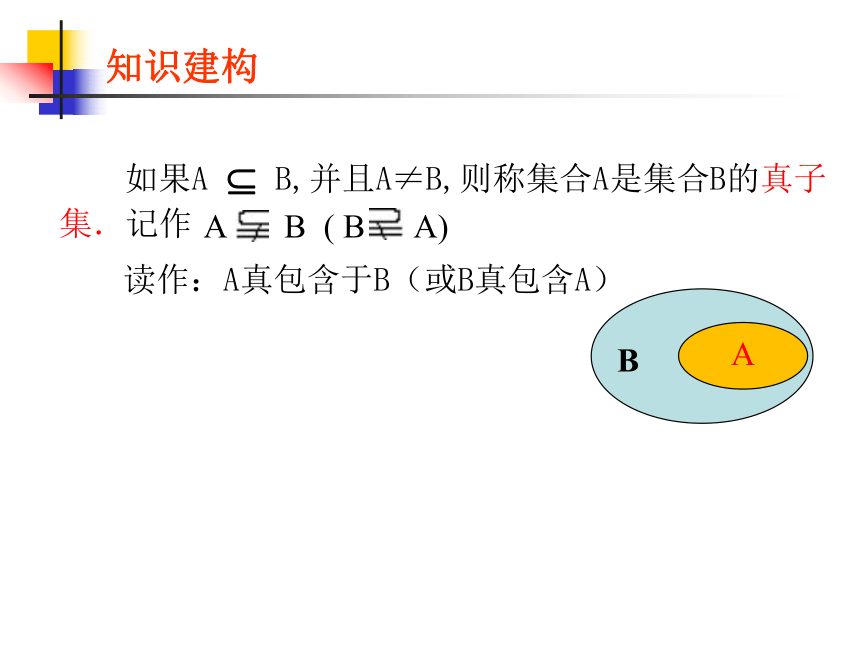
如果A B,并且A≠B,则称集合A是集合B的真子集.记作
A B ( B A)
读作:A真包含于B(或B真包含A)
B
A
知识建构
练习2
1.判断下列说法是否正确,如果不正确,请加以改正
(1) 表示空集;
(2)空集是任何集合的真子集;
(3) 不是 ;
(4) 的所有子集是 , , ;
(5)如果 ,那么A必是B的真子集;
(6) 不能同时成立。
?
?
例1.写出集合{a,b}的所有子集及其真子集;
变式1 写出集合{a,b,c}的所有子集及其真子集;
猜想 {a1,a2,a3,…an }的所有子集共有_个,真子集有 个;非空真子集有 个.
知识应用
变式2 已知集合M满足 ,试写出符合要求的集合M.
S={高一(20)的同学},
A={高一(20) 的男生}
怎么用S与A表示高一(20) 的女生组成的集合?
问题探究二:
设 ,由S中不属于A的所有元素组成的集合,称为集合S的子集A的补集.
记作
知识建构
A
如果集合S包含我们所要研究的各个集合,这
时S可以看做一个全集,全集通常记为U.
注 补集的概念必须要有全集的限制
例2.U={1,2,3,4,5,6,7,8,9},B={3,5,6}
A={3,5,6,8,9},求:
知识应用
例3.不等式组 的解集为A , U=R , 试求A , 及CUA , 并把它们分别表示数轴上.
点评 不等式问题通常借助数轴来研究,但要 注意实心点与空心点.
例4.已知全集U={2 ,3,a2+2a-3} , A={|2a-1| ,2} , Cu A={5} , 求实数a的值.
例5:设集合A={x|x2+4x=0,x∈R},B=
{x|x2+2(a+1)x+a2-1=0,x∈R},若B A,
求实数a的取值范围.
知识拓展
课堂小结
知识 子集
真子集
补集
全集
思想 数形结合
⑴0___N;
⑵ ____Q;
⑶-1.5____R
∈
?
∈
温故知新
观察下列几组集合,试从集合元素的角度分析集合A与集合B的关系
(1)A={1,2,3},B={1,2,3,4,5}
(2)A=N,B=Q
(3)A={-2,4},
(4)A={x|x为北京人}, B={x|x为中国人}
问题探究一
如果集合A中的任意一个元素都是 集合B的元素,那么集合A称为集合B的子集.
记作 A B(或B A)
B
A
读作:A包含于集合B”,或“集合B包含集合A”.
知识建构
判断集合A是否为集合B的子集,若是则在( )打√,若不是则在( )打×:
①A={1,3,5}, B={1,2,3,4,5,6} ( )
②A={1,3,5}, B={1,3,6,9} ( )
③A={0}, B={x x2+2=0} ( )
④A={a,b,c,d}, B={d,b,c,a} ( )
练习1
思考:以下式子成立吗?
⑴A?A;⑵Φ?A;⑶Φ?Φ.
想一想:
1.A?B与B?A能否同时成立?
你能举出一个例子吗?
集合与集合之间的 “相等”关系:
若A?B且B?A,则A=B.
如果A B,并且A≠B,则称集合A是集合B的真子集.记作
A B ( B A)
读作:A真包含于B(或B真包含A)
B
A
知识建构
练习2
1.判断下列说法是否正确,如果不正确,请加以改正
(1) 表示空集;
(2)空集是任何集合的真子集;
(3) 不是 ;
(4) 的所有子集是 , , ;
(5)如果 ,那么A必是B的真子集;
(6) 不能同时成立。
?
?
例1.写出集合{a,b}的所有子集及其真子集;
变式1 写出集合{a,b,c}的所有子集及其真子集;
猜想 {a1,a2,a3,…an }的所有子集共有_个,真子集有 个;非空真子集有 个.
知识应用
变式2 已知集合M满足 ,试写出符合要求的集合M.
S={高一(20)的同学},
A={高一(20) 的男生}
怎么用S与A表示高一(20) 的女生组成的集合?
问题探究二:
设 ,由S中不属于A的所有元素组成的集合,称为集合S的子集A的补集.
记作
知识建构
A
如果集合S包含我们所要研究的各个集合,这
时S可以看做一个全集,全集通常记为U.
注 补集的概念必须要有全集的限制
例2.U={1,2,3,4,5,6,7,8,9},B={3,5,6}
A={3,5,6,8,9},求:
知识应用
例3.不等式组 的解集为A , U=R , 试求A , 及CUA , 并把它们分别表示数轴上.
点评 不等式问题通常借助数轴来研究,但要 注意实心点与空心点.
例4.已知全集U={2 ,3,a2+2a-3} , A={|2a-1| ,2} , Cu A={5} , 求实数a的值.
例5:设集合A={x|x2+4x=0,x∈R},B=
{x|x2+2(a+1)x+a2-1=0,x∈R},若B A,
求实数a的取值范围.
知识拓展
课堂小结
知识 子集
真子集
补集
全集
思想 数形结合
