高一数学 第3课时 交集、并集(1)(19张PPT)
文档属性
| 名称 | 高一数学 第3课时 交集、并集(1)(19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-21 00:00:00 | ||
图片预览






文档简介
1.3 交集、并集(1)
高一数学
一、复习回顾
已知集合S和A,求CSA:
1、S={本班学生},A={本班男生};
2、S=Z,A=N*;
3、S={0},A={0};
4、S=R,A={x|x>1};
5、S={x|1二、继续讨论
求集合A在一个S中的补集CSA的过程实际是由两个集合得到一个集合的过程,称为集合的运算。
用图示分别表示下列各组中的三个集合:
1、A={-1,1,2,3},B={-1,-2,1},C={-1,1};
2、A={x|x≤3},B={x|x>0},C={x|03、A={x|x为高一(4)班语文测验优秀者}B={x|x为高一(4)班英语测验优秀者},C={x|x为高一(4)班语文英语测验都优秀者}。
上述每组集合中A,B,C之间有怎样的关系?
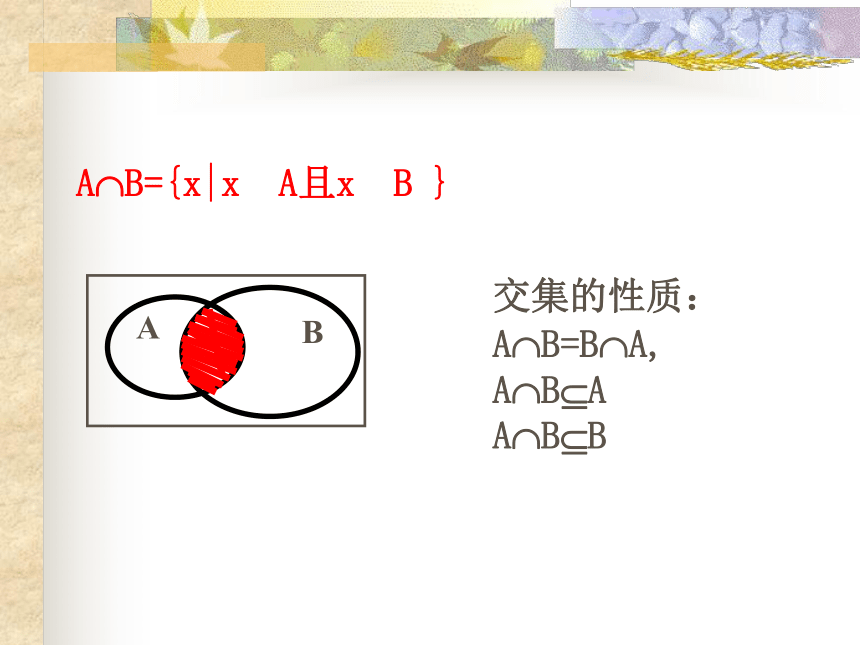
A?B={x|x?A且x?B }
A
B
交集的性质: A?B=B?A, A?B?A A?B?B
1、A={-1,1,2,3},B={-1,-2,1},D={-1,1,2,3,-2};
2、A={x|x为高一(4)班语文测验优秀者},B={x|x为高一(4)班英语测验优秀者},D={x|x为高一(4)班语文或英语测验至少有一门优秀者}。
下列每组集合中A,B,D之间有怎样的关系?
A
B
A
A?B={x|x?A或x?B}
并集的性质: A?B=B?A, A?A?B B? A?B
例1:(1)设A={x|x是等腰三角形},
B= {x|x是直角三角形},求A∩B .
解: A∩B
= {x|x是等腰三角形}∩{x|x是直角三角形}
= {x|x是等腰直角三角形}
(2)设A={x|x是锐角三角形},
B= {x|x是钝角三角形},求A∪B .
解: A∪B
= {x|x是锐角三角形}∪ {x|x是钝角三角形}
= {x|x是斜角三角形}
例2:设 A= {4,5,6,8},B ={3,5,7,8}
求 (1)A∩B (2)A∪B
解:
(1)A∩B ={4,5,6,8}∩ {3,5,7,8}
={5,8}
(2)A∪B ={4,5,6,8}∪{3,5,7,8}
={3,4,5,6,7,8}
例3:设A={x|-1≤x≤2},B={x|1求(1)A∩B (2)A∪B
解:
= { 5,8 },
= {3,4,5,6,7,8};
练习 1:
= { x | 0≤x<5 }.
={x| x>-2 }.
= {x | x是平行四边形}.
= { x | 0≤x<5 }.
={x| x>-2 }.
练习 3:
1.设A={x|x<5},B={x|x?0},
求A?B.
2.设A={x|x>-2},B={x|x?3},
求A∪B.
例4:设A={(x,y)| y=-4x+6},
B={(x,y)|y=5x-3},求A∩B.
解:
A∩B= {(x,y)|y=-4x+6}∩{(x,y)|y=5x-3}
={(1,2)}.
例5:设集合M={a2,2a-1,-4},
P= {1-a,a-5,9},且M?P={9},求a的值 .
解:∵ (CUA) ={1,2,6,7,8},
(CUB) ={1,2,3,5,6},
∴(CUA)∩(CUB) ={1,2,6},
(CUA)∪(CUB) ={1,2,3,5,6,7,8},
∵A∪B={3,4,5 ,7,8} , A ∩B={4}
∴ CU (A∪B) = {1,2,6},
CU (A ∩B) = {1,2,3,5,6,7,8}.
例6:设U={1,2,3,4,5,6,7,8},
A={3,4,5},B={4,7,8},
求 (CUA)∩(CUB), (CUA)∪(CUB) ,
CU (A∪B), CU (A ∩B) .
摩根定律:
(CUA)∩(CUB) = CU (A∪B)
(CUA)∪(CUB) = CU (A∩B)
(CUA)∪ (CUB)
= CU(A∩B)
(CUA)∩(CUB)
= CU(A∪B)
例7:学校举办了排球赛,某班45名同学中有12名同学参赛,后来又举办了田径赛,这个班有20名同学参赛,已知两项都参赛的有6名同学,两项比赛中,这个班共有多少名同学没有参加过比赛?
解:设A={x|x为参加排球赛的同学},B={x|x为参加田径赛的同学},则A∩B ={x|x为参加两项比赛的同学}。
画出Veen图(如图),可知没有参加过比赛的同学有
45-(12+20-6)=19(名)
答:这个班共有19名同学没有参加过比赛。
A
(6)
B
(14)
(6)
变题:某班45名同学,参加数学兴趣小组的有30名同学,参加物理兴趣小组的有25名同学,求既参加数学兴趣小组又参加物理兴趣小组的人数的最大值与最小值?
高一数学
一、复习回顾
已知集合S和A,求CSA:
1、S={本班学生},A={本班男生};
2、S=Z,A=N*;
3、S={0},A={0};
4、S=R,A={x|x>1};
5、S={x|1
求集合A在一个S中的补集CSA的过程实际是由两个集合得到一个集合的过程,称为集合的运算。
用图示分别表示下列各组中的三个集合:
1、A={-1,1,2,3},B={-1,-2,1},C={-1,1};
2、A={x|x≤3},B={x|x>0},C={x|0
上述每组集合中A,B,C之间有怎样的关系?
A?B={x|x?A且x?B }
A
B
交集的性质: A?B=B?A, A?B?A A?B?B
1、A={-1,1,2,3},B={-1,-2,1},D={-1,1,2,3,-2};
2、A={x|x为高一(4)班语文测验优秀者},B={x|x为高一(4)班英语测验优秀者},D={x|x为高一(4)班语文或英语测验至少有一门优秀者}。
下列每组集合中A,B,D之间有怎样的关系?
A
B
A
A?B={x|x?A或x?B}
并集的性质: A?B=B?A, A?A?B B? A?B
例1:(1)设A={x|x是等腰三角形},
B= {x|x是直角三角形},求A∩B .
解: A∩B
= {x|x是等腰三角形}∩{x|x是直角三角形}
= {x|x是等腰直角三角形}
(2)设A={x|x是锐角三角形},
B= {x|x是钝角三角形},求A∪B .
解: A∪B
= {x|x是锐角三角形}∪ {x|x是钝角三角形}
= {x|x是斜角三角形}
例2:设 A= {4,5,6,8},B ={3,5,7,8}
求 (1)A∩B (2)A∪B
解:
(1)A∩B ={4,5,6,8}∩ {3,5,7,8}
={5,8}
(2)A∪B ={4,5,6,8}∪{3,5,7,8}
={3,4,5,6,7,8}
例3:设A={x|-1≤x≤2},B={x|1
解:
= { 5,8 },
= {3,4,5,6,7,8};
练习 1:
= { x | 0≤x<5 }.
={x| x>-2 }.
= {x | x是平行四边形}.
= { x | 0≤x<5 }.
={x| x>-2 }.
练习 3:
1.设A={x|x<5},B={x|x?0},
求A?B.
2.设A={x|x>-2},B={x|x?3},
求A∪B.
例4:设A={(x,y)| y=-4x+6},
B={(x,y)|y=5x-3},求A∩B.
解:
A∩B= {(x,y)|y=-4x+6}∩{(x,y)|y=5x-3}
={(1,2)}.
例5:设集合M={a2,2a-1,-4},
P= {1-a,a-5,9},且M?P={9},求a的值 .
解:∵ (CUA) ={1,2,6,7,8},
(CUB) ={1,2,3,5,6},
∴(CUA)∩(CUB) ={1,2,6},
(CUA)∪(CUB) ={1,2,3,5,6,7,8},
∵A∪B={3,4,5 ,7,8} , A ∩B={4}
∴ CU (A∪B) = {1,2,6},
CU (A ∩B) = {1,2,3,5,6,7,8}.
例6:设U={1,2,3,4,5,6,7,8},
A={3,4,5},B={4,7,8},
求 (CUA)∩(CUB), (CUA)∪(CUB) ,
CU (A∪B), CU (A ∩B) .
摩根定律:
(CUA)∩(CUB) = CU (A∪B)
(CUA)∪(CUB) = CU (A∩B)
(CUA)∪ (CUB)
= CU(A∩B)
(CUA)∩(CUB)
= CU(A∪B)
例7:学校举办了排球赛,某班45名同学中有12名同学参赛,后来又举办了田径赛,这个班有20名同学参赛,已知两项都参赛的有6名同学,两项比赛中,这个班共有多少名同学没有参加过比赛?
解:设A={x|x为参加排球赛的同学},B={x|x为参加田径赛的同学},则A∩B ={x|x为参加两项比赛的同学}。
画出Veen图(如图),可知没有参加过比赛的同学有
45-(12+20-6)=19(名)
答:这个班共有19名同学没有参加过比赛。
A
(6)
B
(14)
(6)
变题:某班45名同学,参加数学兴趣小组的有30名同学,参加物理兴趣小组的有25名同学,求既参加数学兴趣小组又参加物理兴趣小组的人数的最大值与最小值?
