2020--2021学年人教版八年级下册数学第十八章 平行四边形 强化练习(三)(word版含答案)
文档属性
| 名称 | 2020--2021学年人教版八年级下册数学第十八章 平行四边形 强化练习(三)(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 149.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-22 08:18:53 | ||
图片预览



文档简介
2020--2021学年八年级下册数学第十八章
《平行四边形》强化练习(三)
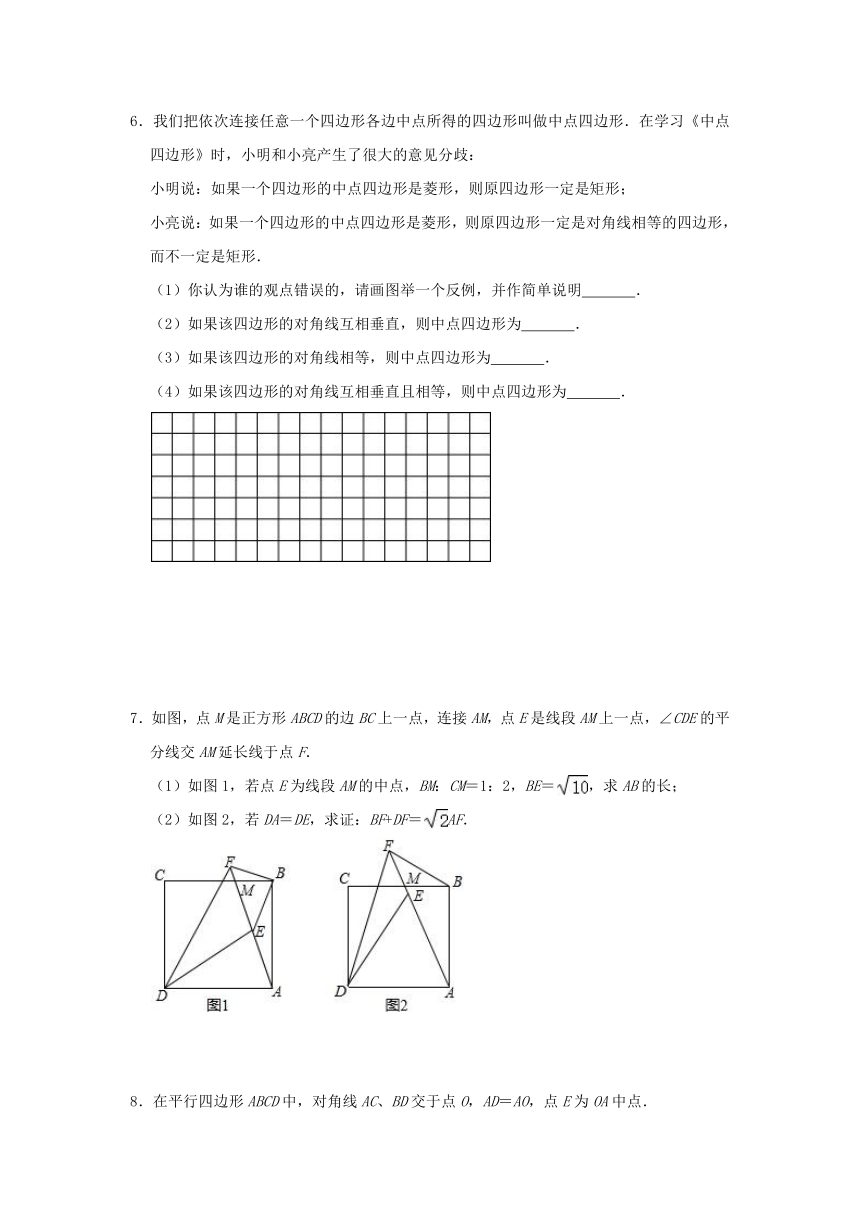
1.如图,已知点A、C在EF上,AD∥BC,DE∥BF,AE=CF.
(1)求证:四边形ABCD是平行四边形;
(2)直接写出图中所有相等的线段(AE=CF除外).
2.已知:在△ABC中,点D为AB上一点,连接CD,∠ADC的平分线交AC于点E,过点E作CD、AB的平行线,分别交AB、CD、BC于点F、M、N.
(1)如图1,求证:四边形DFEM为菱形;
(2)如图2,∠ACB=90°,点D为边AB的中点,连接DN、MF.在不添加任何辅助线的情况下,请直接写出图2中的所有平行四边形(不包括以DF为一边的平行四边形).
3.已知:如图,E,F是正方形ABCD的对角线BD上的两点,且BE=DF.求证:四边形AECF是菱形
4.如图,在菱形ABCD中,E为对角线BD上一点,且AE=DE,连接CE.
(1)求证:CE=DE.
(2)当BE=2,CE=1时,求菱形的边长.
5.如图,?ABCD中,∠A=45°,∠ABD=90°,点F为平行四边形外一点,连接CF、BF,且BF⊥CF于点F.
(1)如图1,若S?ABCD=,CF=5,求BF的长度;
(2)如图2,延长BF、DC交于点E,过点D作DG⊥DF交FC的延长线于点G,若C为DE的中点,求证:CG=CF+EF.
6.我们把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形.在学习《中点四边形》时,小明和小亮产生了很大的意见分歧:
小明说:如果一个四边形的中点四边形是菱形,则原四边形一定是矩形;
小亮说:如果一个四边形的中点四边形是菱形,则原四边形一定是对角线相等的四边形,而不一定是矩形.
(1)你认为谁的观点错误的,请画图举一个反例,并作简单说明
.
(2)如果该四边形的对角线互相垂直,则中点四边形为
.
(3)如果该四边形的对角线相等,则中点四边形为
.
(4)如果该四边形的对角线互相垂直且相等,则中点四边形为
.
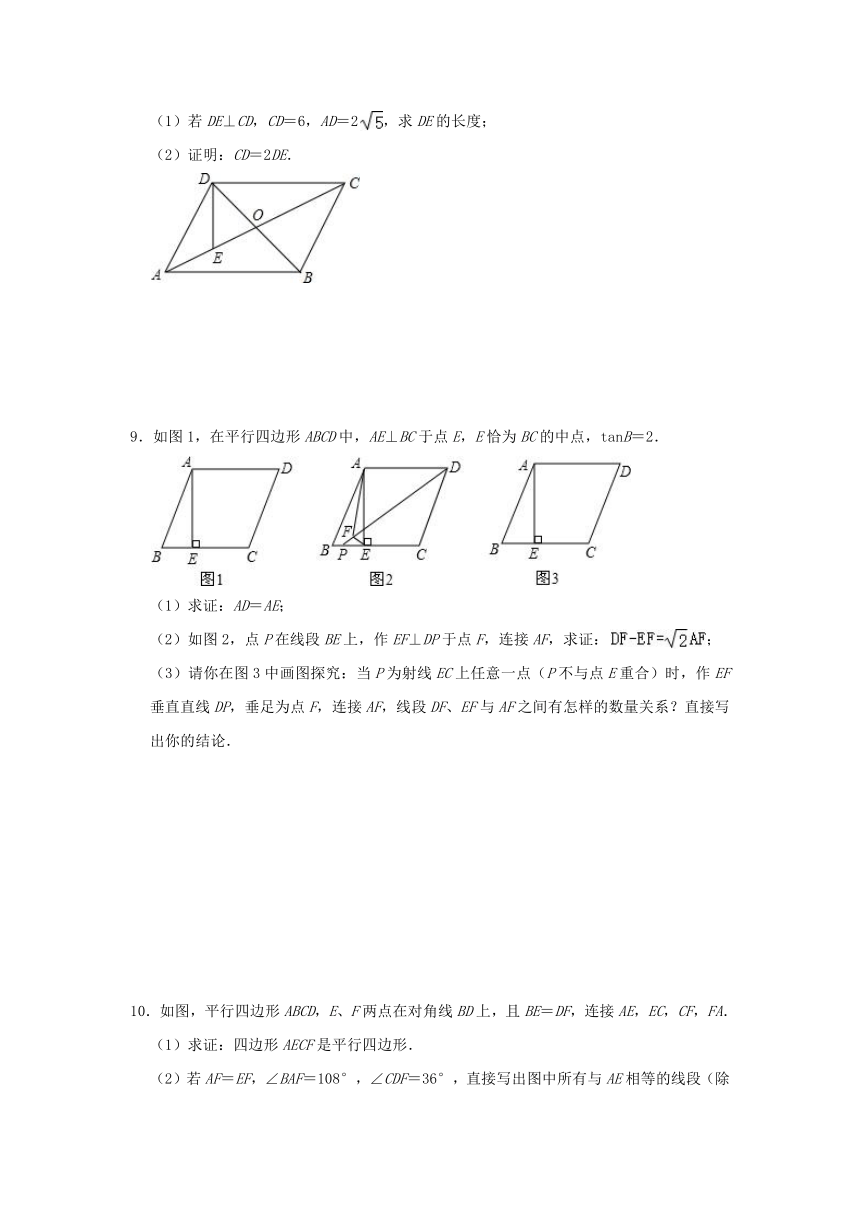
7.如图,点M是正方形ABCD的边BC上一点,连接AM,点E是线段AM上一点,∠CDE的平分线交AM延长线于点F.
(1)如图1,若点E为线段AM的中点,BM:CM=1:2,BE=,求AB的长;
(2)如图2,若DA=DE,求证:BF+DF=AF.
8.在平行四边形ABCD中,对角线AC、BD交于点O,AD=AO,点E为OA中点.
(1)若DE⊥CD,CD=6,AD=2,求DE的长度;
(2)证明:CD=2DE.
9.如图1,在平行四边形ABCD中,AE⊥BC于点E,E恰为BC的中点,tanB=2.
(1)求证:AD=AE;
(2)如图2,点P在线段BE上,作EF⊥DP于点F,连接AF,求证:;
(3)请你在图3中画图探究:当P为射线EC上任意一点(P不与点E重合)时,作EF垂直直线DP,垂足为点F,连接AF,线段DF、EF与AF之间有怎样的数量关系?直接写出你的结论.
10.如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF,FA.
(1)求证:四边形AECF是平行四边形.
(2)若AF=EF,∠BAF=108°,∠CDF=36°,直接写出图中所有与AE相等的线段(除AE外).
参考答案
1.(1)证明:∵AD∥BC,DE∥BF,
∴∠E=∠F,∠DAC=∠BCA,
∴∠DAE=∠BCF,
在△ADE和△CBF中,,
∴△ADE≌△CBF(ASA),
∴AD=CB,
∴四边形ABCD是平行四边形;
(2)解:AD=BC、EC=AF、ED=BF、AB=DC;理由如下:
∵△ADE≌△CBF,
∴AD=BC,ED=BF,
∵AE=CF,
∴EC=AF,
∵四边形ABCD是平行四边形,
∴AB=DC.
2.(1)证明:∵EM∥AB,
∴∠DEM=∠EDF,
∵EF∥CD,
∴四边形DFEM为平行四边形,
∵∠ADC的平分线交AC于点E,
∴∠EDM=∠EDF,
∴∠EDM=∠DEM,
∴ME=MD,
∴四边形DFEM为菱形;
(2)除以DF为一边的平行四边形外的所有平行四边形分别是:?CEDN,?BDEN,?EMFA,?CMFE,?AEND.
3.证明:如图,连接AC交BD于点O,
∵四边形ABCD是正方形,
∴AO=CO,BO=DO,AC⊥BD,
∵BE=DF
∴DO﹣DF=BO﹣BE
∴FO=EO,且AO=CO
∴四边形AECF是平行四边形,
又∵AC⊥BD
∴四边形AECF是菱形
4.(1)证明:∵四边形ABCD是菱形,
∴∠ABE=∠CBE,AB=CB,
在△ABE和△CBE中,
,
∴△ABE≌△CBE(SAS),
∴AE=CE,
∵AE=DE,
∴CE=DE;
(2)解:如图,连接AC交BD于H,
∵四边形ABCD是菱形,
∴AH⊥BD,BH=DH,AH=CH,
∵CE=DE=AE=1,
∴BD=BE+DE=2+1=3,
∴BH=BD=,EH=BE﹣BH=2﹣=,
在Rt△AHE中,由勾股定理得:AH===,
在Rt△AHB中,由勾股定理得:AB===,
∴菱形的边长为.
5.解:(1)如图1,∵四边形ABCD是平行四边形
∴AB∥CD,AB=CD,AD=BC
∴∠BDC=∠ABD=90°
∵BD=DB
∴△ABD≌△CDB
∵∠A=45°
∴△ABD、△BCD是等腰直角三角形
∴BD=AB,AD=AB
∵S?ABCD=,
∴AB?BD=,
∴AB=BD=
∴BC=AD=13
∵BF⊥CF
∴∠BFC=90°
∴BF===12;
(2)如图2,在线段CG上截取CM=CF,连接DM,
∵C为DE的中点,
∴CD=CE
在△CDM和△CEF中
∴△CDM≌△CEF(SAS)
∴DM=EF,∠DMC=∠EFC=90°
∴∠DMG=90°
∵DG⊥DF
∴∠FDG=90°=∠BDC
∴∠GDC+∠EDF=∠BDF+∠EDF
∴∠GDC=∠BDF
由(1)知:△BCD是等腰直角三角形
∴BD=CD,∠CBD=∠BCD=45°
∵∠BDC+∠BFC=90°+90°=180°
∴∠DBF+∠DCF=180°
∵∠DCG+∠DCF=180°
∴∠DCG=∠DBF
∴△DCG≌△DBF(ASA)
∴DG=DF
∴△DFG是等腰直角三角形
∴∠G=45°
∴∠GDM=∠G=45°
∴MG=DM
∴MG=EF
∴CG=CM+MG=CF+EF.
6.解:(1)我认为小明的观点是错误的,反例如图所示.
在等腰梯形ABCD中
AC=BD,
∵M、Q是AB、AD的中点,
∴MQ∥BD,MQ=BD,
同理NP∥BD,NP=BD,
可得四边形MNPQ是平行四边形,
再由MN=PN可得四边形MNPQ是菱形,
(2)∵四边形的对角线互相垂直,
∴它的中点四边形为矩形,
(3)∵四边形的对角线相等,
∴它的中点四边形为菱形,
(4)∵四边形的对角线互相垂直且相等,
∴它的中点四边形为正方形.
7.解:(1)设BM=x,则CM=2x,BC=3x,
∵BA=BC,∴BA=3x.
在Rt△ABM中,E为斜边AM中点,
∴AM=2BE=2.
由勾股定理可得AM2=MB2+AB2,
即40=x2+9x2,解得x=2.
∴AB=3x=6.
(2)延长FD交过点A作垂直于AF的直线于H点,过点D作DP⊥AF于P点.
∵DF平分∠CDE,
∴∠1=∠2.
∵DE=DA,DP⊥AF
∴∠3=∠4.
∵∠1+∠2+∠3+∠4=90°,
∴∠2+∠3=45°.
∴∠DFP=90°﹣45°=45°.
∴AH=AF.
∵∠BAF+∠DAF=90°,∠HAD+∠DAF=90°,
∴∠BAF=∠DAH.
又AB=AD,
∴△ABF≌△ADH(SAS).
∴AF=AH,BF=DH.
∵Rt△FAH是等腰直角三角形,
∴HF=AF.
∵HF=DH+DF=BF+DF,
∴BF+DF=AF.
8.解:(1)∵四边形ABCD是平行四边形,
∴OA=OC,
∵点E为OA中点,AD=AO,AD=2,
∴OE=,OC=2,
∴CE=OE+OC=3,
∵DE⊥CD,CD=6,
∴DE==3;
(2)证明:取AD的中点F,连接OF,
∵AD=AO,点E为OA中点,
∴AE=AF,
在△ADE和△AOF中,
,
∴△ADE≌△AOF(SAS),
∴DE=OF,
∵OA=OC,AF=DF,
∴CD=2OF,
∴CD=2DE.
9.(1)证明:∵tanB=2,
∴AE=2BE;
∵E是BC中点,
∴BC=2BE,
即AE=BC;
又∵四边形ABCD是平行四边形,则AD=BC=AE;
(2)证明:作AG⊥AF,交DP于G;(如图2)
∵AD∥BC,
∴∠ADG=∠DPC;
∵∠AEP=∠EFP=90°,
∴∠PEF+∠EPF=∠PEF+∠AEF=90°,
即∠ADG=∠AEF=∠FPE;
又∵AE=AD,∠FAE=∠GAD=90°﹣∠EAG,
∴△AFE≌△AGD,
∴AF=AG,即△AFG是等腰直角三角形,且EF=DG;
∴FG=AF,且DF=DG+GF=EF+FG,
故DF﹣EF=AF;
(3)解:如图3,
①当EP在线段BC上时,有DF+EF=AF
②当EP≤2BC时,DF﹣EF=AF,解法同(2).
③当EP>2BC时,EF﹣DF=AF.
10.(1)证明:如图,连接AC交BD于点O,
在?ABCD中,OA=OC,OB=OD,
∵BE=DF,
∴OB﹣BE=OD﹣DF,
即OE=OF,
∴四边形AECF是平行四边形(对角线互相平分的四边形是平行四边形);
(2)解:∵AB∥CD,
∴∠ABF=∠CDF=36°,
∵AF=EF,
∴∠FAE=∠FEA=72°,
∵∠AEF=∠EBA+∠EAB,
∴∠EBA=∠EAB=36°,
∴EA=EB,
同理可证CF=DF,
∵AE=CF,
∴与AE相等的线段有BE、CF、DF.
《平行四边形》强化练习(三)
1.如图,已知点A、C在EF上,AD∥BC,DE∥BF,AE=CF.
(1)求证:四边形ABCD是平行四边形;
(2)直接写出图中所有相等的线段(AE=CF除外).
2.已知:在△ABC中,点D为AB上一点,连接CD,∠ADC的平分线交AC于点E,过点E作CD、AB的平行线,分别交AB、CD、BC于点F、M、N.
(1)如图1,求证:四边形DFEM为菱形;
(2)如图2,∠ACB=90°,点D为边AB的中点,连接DN、MF.在不添加任何辅助线的情况下,请直接写出图2中的所有平行四边形(不包括以DF为一边的平行四边形).
3.已知:如图,E,F是正方形ABCD的对角线BD上的两点,且BE=DF.求证:四边形AECF是菱形
4.如图,在菱形ABCD中,E为对角线BD上一点,且AE=DE,连接CE.
(1)求证:CE=DE.
(2)当BE=2,CE=1时,求菱形的边长.
5.如图,?ABCD中,∠A=45°,∠ABD=90°,点F为平行四边形外一点,连接CF、BF,且BF⊥CF于点F.
(1)如图1,若S?ABCD=,CF=5,求BF的长度;
(2)如图2,延长BF、DC交于点E,过点D作DG⊥DF交FC的延长线于点G,若C为DE的中点,求证:CG=CF+EF.
6.我们把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形.在学习《中点四边形》时,小明和小亮产生了很大的意见分歧:
小明说:如果一个四边形的中点四边形是菱形,则原四边形一定是矩形;
小亮说:如果一个四边形的中点四边形是菱形,则原四边形一定是对角线相等的四边形,而不一定是矩形.
(1)你认为谁的观点错误的,请画图举一个反例,并作简单说明
.
(2)如果该四边形的对角线互相垂直,则中点四边形为
.
(3)如果该四边形的对角线相等,则中点四边形为
.
(4)如果该四边形的对角线互相垂直且相等,则中点四边形为
.
7.如图,点M是正方形ABCD的边BC上一点,连接AM,点E是线段AM上一点,∠CDE的平分线交AM延长线于点F.
(1)如图1,若点E为线段AM的中点,BM:CM=1:2,BE=,求AB的长;
(2)如图2,若DA=DE,求证:BF+DF=AF.
8.在平行四边形ABCD中,对角线AC、BD交于点O,AD=AO,点E为OA中点.
(1)若DE⊥CD,CD=6,AD=2,求DE的长度;
(2)证明:CD=2DE.
9.如图1,在平行四边形ABCD中,AE⊥BC于点E,E恰为BC的中点,tanB=2.
(1)求证:AD=AE;
(2)如图2,点P在线段BE上,作EF⊥DP于点F,连接AF,求证:;
(3)请你在图3中画图探究:当P为射线EC上任意一点(P不与点E重合)时,作EF垂直直线DP,垂足为点F,连接AF,线段DF、EF与AF之间有怎样的数量关系?直接写出你的结论.
10.如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF,FA.
(1)求证:四边形AECF是平行四边形.
(2)若AF=EF,∠BAF=108°,∠CDF=36°,直接写出图中所有与AE相等的线段(除AE外).
参考答案
1.(1)证明:∵AD∥BC,DE∥BF,
∴∠E=∠F,∠DAC=∠BCA,
∴∠DAE=∠BCF,
在△ADE和△CBF中,,
∴△ADE≌△CBF(ASA),
∴AD=CB,
∴四边形ABCD是平行四边形;
(2)解:AD=BC、EC=AF、ED=BF、AB=DC;理由如下:
∵△ADE≌△CBF,
∴AD=BC,ED=BF,
∵AE=CF,
∴EC=AF,
∵四边形ABCD是平行四边形,
∴AB=DC.
2.(1)证明:∵EM∥AB,
∴∠DEM=∠EDF,
∵EF∥CD,
∴四边形DFEM为平行四边形,
∵∠ADC的平分线交AC于点E,
∴∠EDM=∠EDF,
∴∠EDM=∠DEM,
∴ME=MD,
∴四边形DFEM为菱形;
(2)除以DF为一边的平行四边形外的所有平行四边形分别是:?CEDN,?BDEN,?EMFA,?CMFE,?AEND.
3.证明:如图,连接AC交BD于点O,
∵四边形ABCD是正方形,
∴AO=CO,BO=DO,AC⊥BD,
∵BE=DF
∴DO﹣DF=BO﹣BE
∴FO=EO,且AO=CO
∴四边形AECF是平行四边形,
又∵AC⊥BD
∴四边形AECF是菱形
4.(1)证明:∵四边形ABCD是菱形,
∴∠ABE=∠CBE,AB=CB,
在△ABE和△CBE中,
,
∴△ABE≌△CBE(SAS),
∴AE=CE,
∵AE=DE,
∴CE=DE;
(2)解:如图,连接AC交BD于H,
∵四边形ABCD是菱形,
∴AH⊥BD,BH=DH,AH=CH,
∵CE=DE=AE=1,
∴BD=BE+DE=2+1=3,
∴BH=BD=,EH=BE﹣BH=2﹣=,
在Rt△AHE中,由勾股定理得:AH===,
在Rt△AHB中,由勾股定理得:AB===,
∴菱形的边长为.
5.解:(1)如图1,∵四边形ABCD是平行四边形
∴AB∥CD,AB=CD,AD=BC
∴∠BDC=∠ABD=90°
∵BD=DB
∴△ABD≌△CDB
∵∠A=45°
∴△ABD、△BCD是等腰直角三角形
∴BD=AB,AD=AB
∵S?ABCD=,
∴AB?BD=,
∴AB=BD=
∴BC=AD=13
∵BF⊥CF
∴∠BFC=90°
∴BF===12;
(2)如图2,在线段CG上截取CM=CF,连接DM,
∵C为DE的中点,
∴CD=CE
在△CDM和△CEF中
∴△CDM≌△CEF(SAS)
∴DM=EF,∠DMC=∠EFC=90°
∴∠DMG=90°
∵DG⊥DF
∴∠FDG=90°=∠BDC
∴∠GDC+∠EDF=∠BDF+∠EDF
∴∠GDC=∠BDF
由(1)知:△BCD是等腰直角三角形
∴BD=CD,∠CBD=∠BCD=45°
∵∠BDC+∠BFC=90°+90°=180°
∴∠DBF+∠DCF=180°
∵∠DCG+∠DCF=180°
∴∠DCG=∠DBF
∴△DCG≌△DBF(ASA)
∴DG=DF
∴△DFG是等腰直角三角形
∴∠G=45°
∴∠GDM=∠G=45°
∴MG=DM
∴MG=EF
∴CG=CM+MG=CF+EF.
6.解:(1)我认为小明的观点是错误的,反例如图所示.
在等腰梯形ABCD中
AC=BD,
∵M、Q是AB、AD的中点,
∴MQ∥BD,MQ=BD,
同理NP∥BD,NP=BD,
可得四边形MNPQ是平行四边形,
再由MN=PN可得四边形MNPQ是菱形,
(2)∵四边形的对角线互相垂直,
∴它的中点四边形为矩形,
(3)∵四边形的对角线相等,
∴它的中点四边形为菱形,
(4)∵四边形的对角线互相垂直且相等,
∴它的中点四边形为正方形.
7.解:(1)设BM=x,则CM=2x,BC=3x,
∵BA=BC,∴BA=3x.
在Rt△ABM中,E为斜边AM中点,
∴AM=2BE=2.
由勾股定理可得AM2=MB2+AB2,
即40=x2+9x2,解得x=2.
∴AB=3x=6.
(2)延长FD交过点A作垂直于AF的直线于H点,过点D作DP⊥AF于P点.
∵DF平分∠CDE,
∴∠1=∠2.
∵DE=DA,DP⊥AF
∴∠3=∠4.
∵∠1+∠2+∠3+∠4=90°,
∴∠2+∠3=45°.
∴∠DFP=90°﹣45°=45°.
∴AH=AF.
∵∠BAF+∠DAF=90°,∠HAD+∠DAF=90°,
∴∠BAF=∠DAH.
又AB=AD,
∴△ABF≌△ADH(SAS).
∴AF=AH,BF=DH.
∵Rt△FAH是等腰直角三角形,
∴HF=AF.
∵HF=DH+DF=BF+DF,
∴BF+DF=AF.
8.解:(1)∵四边形ABCD是平行四边形,
∴OA=OC,
∵点E为OA中点,AD=AO,AD=2,
∴OE=,OC=2,
∴CE=OE+OC=3,
∵DE⊥CD,CD=6,
∴DE==3;
(2)证明:取AD的中点F,连接OF,
∵AD=AO,点E为OA中点,
∴AE=AF,
在△ADE和△AOF中,
,
∴△ADE≌△AOF(SAS),
∴DE=OF,
∵OA=OC,AF=DF,
∴CD=2OF,
∴CD=2DE.
9.(1)证明:∵tanB=2,
∴AE=2BE;
∵E是BC中点,
∴BC=2BE,
即AE=BC;
又∵四边形ABCD是平行四边形,则AD=BC=AE;
(2)证明:作AG⊥AF,交DP于G;(如图2)
∵AD∥BC,
∴∠ADG=∠DPC;
∵∠AEP=∠EFP=90°,
∴∠PEF+∠EPF=∠PEF+∠AEF=90°,
即∠ADG=∠AEF=∠FPE;
又∵AE=AD,∠FAE=∠GAD=90°﹣∠EAG,
∴△AFE≌△AGD,
∴AF=AG,即△AFG是等腰直角三角形,且EF=DG;
∴FG=AF,且DF=DG+GF=EF+FG,
故DF﹣EF=AF;
(3)解:如图3,
①当EP在线段BC上时,有DF+EF=AF
②当EP≤2BC时,DF﹣EF=AF,解法同(2).
③当EP>2BC时,EF﹣DF=AF.
10.(1)证明:如图,连接AC交BD于点O,
在?ABCD中,OA=OC,OB=OD,
∵BE=DF,
∴OB﹣BE=OD﹣DF,
即OE=OF,
∴四边形AECF是平行四边形(对角线互相平分的四边形是平行四边形);
(2)解:∵AB∥CD,
∴∠ABF=∠CDF=36°,
∵AF=EF,
∴∠FAE=∠FEA=72°,
∵∠AEF=∠EBA+∠EAB,
∴∠EBA=∠EAB=36°,
∴EA=EB,
同理可证CF=DF,
∵AE=CF,
∴与AE相等的线段有BE、CF、DF.
